2. Matemáticas de la Aprendizaje Profundo

“Todos los números están compuestos por unidades, y todos los números se pueden dividir en unidades” - Al-Khwarizmi (780-850), matemático persa.

En este capítulo, examinaremos los conceptos matemáticos fundamentales que constituyen el núcleo del aprendizaje profundo. Los modelos de aprendizaje profundo están compuestos por combinaciones de funciones matemáticas complejas. Un entendimiento profundo del álgebra lineal, cálculo, probabilidad y estadística es esencial para comprender el funcionamiento de los modelos, mejorar su rendimiento y diseñar nuevos modelos. Por ejemplo, la comprensión de las operaciones matriciales es crucial para entender cómo funciona una Red Neuronal Convolucional (CNN), mientras que la diferenciación y optimización juegan un papel fundamental en la comprensión del proceso de aprendizaje de los modelos.

Si este capítulo resulta difícil, puede pasar al siguiente. Es aconsejable volver periódicamente para familiarizarse con el contenido.

2.1 Fundamentos del Álgebra Lineal

El álgebra lineal es la base fundamental del aprendizaje profundo. Desde las operaciones matriciales hasta técnicas de optimización avanzadas, el álgebra lineal es una herramienta esencial. En esta sección, abordaremos desde los conceptos básicos como vectores, matrices y tensores hasta temas avanzados como la descomposición en valores singulares y el análisis de componentes principales.

2.1.1 Vectores

Los vectores y las matrices son las operaciones fundamentales para representar datos y transformar cada dato.

Conceptos básicos de los vectores

Un vector es un objeto matemático que representa una cantidad con magnitud y dirección. La definición matemática es la misma, pero la perspectiva puede variar ligeramente dependiendo del campo de aplicación.

• Perspectiva matemática: En matemáticas, un vector se define como un objeto abstracto con magnitud y dirección. Como elemento de un espacio vectorial, posee las propiedades de estar cerrado bajo la suma y el producto por escalares.
• Perspectiva física: En física, los vectores se utilizan principalmente para representar cantidades físicas como fuerza, velocidad y aceleración. En este caso, la magnitud y dirección del vector tienen un significado físico real. La física trata todos los cambios como vectores, y las dimensiones de los vectores son limitadas. Por ejemplo, el espacio es tridimensional y el espacio-tiempo cuatridimensional.
• Perspectiva de ciencias de la computación: En ciencias de la computación, especialmente en aprendizaje automático y aprendizaje profundo, los vectores se utilizan principalmente para representar características (features) de los datos. Cada elemento del vector representa una característica específica de los datos y no necesariamente tiene una dirección física. Para representar características, las dimensiones del vector pueden variar desde decenas hasta miles.

Entender estas perspectivas diversas es importante al trabajar con vectores en el aprendizaje profundo. Aunque en el aprendizaje profundo se utilizan principalmente los vectores desde la perspectiva de ciencias de la computación, también se aplican conceptos matemáticos y intuiciones físicas.

En el aprendizaje profundo, los vectores se utilizan principalmente para representar simultáneamente varias características de los datos. Por ejemplo, un vector de 5 dimensiones utilizado en un modelo de predicción de precios de viviendas puede expresarse como sigue:

\(\mathbf{v} = \begin{bmatrix} v_1 \ v_2 \ v_3 \ v_4 \ v_5 \end{bmatrix}\)

Cada elemento de este vector representa una característica diferente de la vivienda. \(v_1\): área de la vivienda (en metros cuadrados), \(v_2\): número de habitaciones, \(v_3\): edad de la vivienda (en años), \(v_4\): distancia a escuelas cercanas (en kilómetros), \(v_5\): tasa de criminalidad (porcentaje)

Los modelos de aprendizaje profundo pueden usar estos vectores multidimensionales como entrada para predecir el precio de una vivienda. De esta manera, los vectores se utilizan para representar y procesar eficazmente las diversas características de datos complejos del mundo real.

En NumPy, los vectores se pueden crear y utilizar fácilmente.

!pip install dldna[colab] # in Colab

# !pip install dldna[all] # in your local

import numpy as np

# Vector creation
v = np.array([1, 2, 3])

# Vector magnitude (L2 norm)
magnitude = np.linalg.norm(v)
print(f"Vector magnitude: {magnitude}")

# Vector normalization
normalized_v = v / magnitude
print(f"Normalized vector: {normalized_v}")

Vector magnitude: 3.7416573867739413
Normalized vector: [0.26726124 0.53452248 0.80178373]

Si exploramos más a fondo el concepto de vector, encontramos la distinción entre vectores fila y vectores columna, así como los conceptos de covectores (vectores covariantes) y contravectores (vectores contravariantes), que se utilizan en física e ingeniería.

Vectores fila y vectores columna

Los vectores se representan generalmente como vectores columna. Los vectores fila pueden considerarse la transpuesta de los vectores columna. Matemáticamente, con mayor precisión, un vector fila también puede llamarse covector (dual vector).

Vector columna: \(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}\), Vector fila: \(\mathbf{v}^T = [v_1 \quad v_2 \quad v_3]\)

Los vectores fila y los vectores columna tienen propiedades diferentes. Un vector fila actúa como una función lineal sobre un vector columna para producir un escalar. Esto se expresa mediante el producto interno.

\[\mathbf{u}^T\mathbf{v} = u_1v_1 + u_2v_2 + u_3v_3\]

Covectores y contravectores

En física e ingeniería, los conceptos de covector (vector covariante) y contravector (vector contravariante) son tratados con importancia. Estos describen las características de transformación de un vector bajo cambios en el sistema de coordenadas.

• Contravector: Un vector que se transforma en la dirección opuesta a la base cuando cambia el sistema de coordenadas. Generalmente se denota con un superíndice (por ejemplo, \(v^i\)).
• Covector: Un vector que se transforma en la misma dirección que la base cuando cambia el sistema de coordenadas. Generalmente se denota con un subíndice (por ejemplo, \(v_i\)).

En la notación tensorial, esta distinción es crucial. Por ejemplo, \(T^i_j\) indica que el superíndice \(i\) representa contravarianza y el subíndice \(j\) representa covarianza. En teoría de la relatividad general, estos conceptos de covarianza y contravarianza son tratados como fundamentales.

Aplicación en aprendizaje profundo

En el aprendizaje profundo, la distinción entre covarianza y contravarianza a menudo no se enfatiza explícitamente. Esto se debe a las siguientes razones:

1. Representación estandarizada de datos: En el aprendizaje profundo, los datos generalmente se manejan en una forma estandarizada (por ejemplo, vectores columna), lo que hace que la distinción entre covarianza y contravarianza sea menos importante.
2. Suposición del espacio euclidiano: Muchos modelos de aprendizaje profundo asumen que los datos residen en un espacio euclidiano, donde la distinción entre covarianza y contravarianza no es clara.
3. Simplificación de operaciones: Las principales operaciones en el aprendizaje profundo (por ejemplo, multiplicación matricial, aplicación de funciones de activación) pueden realizarse eficazmente sin esta distinción.
4. Diferenciación automática: Las funciones de diferenciación automática en los frameworks modernos de aprendizaje profundo pueden calcular gradientes precisos sin necesidad de estas distinciones detalladas.

Sin embargo, en ciertos campos, particularmente en el aprendizaje de máquinas basado en física o en el aprendizaje profundo geométrico, estos conceptos aún son importantes. Por ejemplo, en modelos de aprendizaje profundo que utilizan geometría diferencial, la distinción entre covarianza y contravarianza puede desempeñar un papel crucial en el diseño e interpretación del modelo.

En conclusión, aunque los conceptos básicos de vectores en el aprendizaje profundo se usan de manera simplificada, ideas matemáticas más complejas siguen siendo importantes en el diseño avanzado de modelos y aplicaciones específicas.

Haga clic para ver el contenido (buceo profundo: espacio vectorial y combinación lineal)

Espacio vectorial y combinación lineal

El espacio vectorial, un concepto fundamental del álgebra lineal, proporciona el marco básico para representar y transformar datos en el aprendizaje profundo. En este análisis detallado, examinamos la definición rigurosa de los espacios vectoriales y conceptos relacionados, así como ejemplos de su aplicación en el aprendizaje profundo.

Espacio Vectorial (Vector Space)

Un espacio vectorial es un conjunto \(V\) que satisface las siguientes 8 axiomas, junto con las operaciones de adición y multiplicación escalar. Aquí, los elementos de \(V\) se denominan vectores, y los escalares son elementos del conjunto de números reales \(\mathbb{R}\) o complejos \(\mathbb{C}\). (En el aprendizaje profundo, se utilizan principalmente números reales).

Adición vectorial (Vector Addition): Para cualquier par de elementos \(\mathbf{u}, \mathbf{v}\) en \(V\), \(\mathbf{u} + \mathbf{v}\) también es un elemento de \(V\). (Cerrado bajo adición, closed under addition)

Multiplicación escalar (Scalar Multiplication): Para cualquier elemento \(\mathbf{u}\) en \(V\) y cualquier escalar \(c\), \(c\mathbf{u}\) también es un elemento de \(V\). (Cerrado bajo multiplicación escalar, closed under scalar multiplication)

La adición vectorial y la multiplicación escalar deben satisfacer los siguientes 8 axiomas. (\(\mathbf{u}, \mathbf{v}, \mathbf{w} \in V\), \(c, d\): escalares)

1. Conmutatividad de la adición (Commutativity of addition): \(\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}\)
2. Asociatividad de la adición (Associativity of addition): \((\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w})\)
3. Elemento neutro de la adición (Additive identity): Existe un \(\mathbf{0} \in V\) (vector cero) tal que para todo \(\mathbf{u} \in V\), se cumple \(\mathbf{u} + \mathbf{0} = \mathbf{u}\).
4. Elemento inverso de la adición (Additive inverse): Para cada \(\mathbf{u} \in V\), existe un \(-\mathbf{u} \in V\) (elemento inverso) tal que \(\mathbf{u} + (-\mathbf{u}) = \mathbf{0}\).
5. Distributividad de la multiplicación escalar con respecto a la adición vectorial (Distributivity of scalar multiplication with respect to vector addition): \(c(\mathbf{u} + \mathbf{v}) = c\mathbf{u} + c\mathbf{v}\)
6. Distributividad de la multiplicación escalar con respecto a la adición escalar (Distributivity of scalar multiplication with respect to scalar addition): \((c + d)\mathbf{u} = c\mathbf{u} + d\mathbf{u}\)
7. Asociatividad de la multiplicación escalar con respecto a la multiplicación escalar (Compatibility of scalar multiplication with scalar multiplication): \(c(d\mathbf{u}) = (cd)\mathbf{u}\)
8. Elemento neutro de la multiplicación escalar (Identity element of scalar multiplication): \(1\mathbf{u} = \mathbf{u}\) (donde 1 es el elemento neutro de la multiplicación escalar)

Ejemplo: * \(\mathbb{R}^n\): espacio vectorial real de \(n\) dimensiones (n-uplas de números reales) * \(\mathbb{C}^n\): espacio vectorial complejo de \(n\) dimensiones * \(M_{m \times n}(\mathbb{R})\): espacio de matrices reales de \(m \times n\) * \(P_n\): espacio de polinomios con coeficientes reales de grado \(\leq n\) * \(C[a, b]\): espacio de funciones valoradas en los reales continuas en el intervalo \([a, b]\)

Subespacio

Un subconjunto \(W\) del espacio vectorial \(V\) es un subespacio si cumple las siguientes condiciones:

1. \(\mathbf{0} \in W\) (contiene al vector cero)
2. Si \(\mathbf{u}, \mathbf{v} \in W\), entonces \(\mathbf{u} + \mathbf{v} \in W\) (cerrado bajo adición)
3. Si \(\mathbf{u} \in W\) y \(c\) es un escalar, entonces \(c\mathbf{u} \in W\) (cerrado bajo multiplicación escalar)

Es decir, un subespacio es un subconjunto de un espacio vectorial que también cumple con las propiedades de un espacio vectorial.

Combinación lineal

Dada una colección de vectores \(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\) en el espacio vectorial \(V\) y escalares \(c_1, c_2, ..., c_k\), la expresión siguiente se llama combinación lineal:

\(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + ... + c_k\mathbf{v}_k\)

Independencia lineal y dependencia lineal

Un conjunto de vectores {\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} es linealmente independiente si la única solución a la ecuación

\(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + ... + c_k\mathbf{v}_k = \mathbf{0}\)

es \(c_1 = c_2 = ... = c_k = 0\).

Si no se cumple esta condición (es decir, existen escalares no todos nulos \(c_1, ..., c_k\) que satisfacen la ecuación anterior), el conjunto de vectores es linealmente dependiente.

Significado intuitivo:

• Independencia lineal: los vectores pueden pensarse como apuntando en “direcciones diferentes”. Ningún vector puede ser expresado como una combinación lineal de los demás.
• Dependencia lineal: algunos de los vectores pueden estar en la “misma dirección” (o “plano”, “hiperplano”). Un vector puede ser expresado como una combinación lineal de los otros.

Base y dimensión

• Base: un conjunto de vectores del espacio vectorial \(V\) es una base si:
  1. Son linealmente independientes.
  2. Span a \(V\) (véase explicación de span a continuación).
• Dimensión: el número de vectores en una base se llama dimensión. (dim \(V\))

Clave: aunque una base para un espacio vectorial dado no es única, todas las bases tienen el mismo número de vectores.

Span

El span de un conjunto de vectores {\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} es el conjunto de todas las posibles combinaciones lineales de estos vectores.

span{\(\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_k\)} = {\(c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + ... + c_k\mathbf{v}_k\) | \(c_1, c_2, ..., c_k\) son escalares}

En otras palabras, es el conjunto de todos los vectores que se pueden formar usando los vectores dados. El span siempre forma un subespacio. #### Ejemplos de espacios vectoriales en el aprendizaje profundo

• Vector de características (Feature Vector): los datos de entrada para modelos de aprendizaje profundo, como imágenes, texto y audio, a menudo se representan como vectores de alta dimensión. Por ejemplo, una imagen en escala de grises de 28x28 píxeles puede representarse como un vector de 784 dimensiones. Cada dimensión representa el valor de brillo de un píxel específico de la imagen.
• Vector de pesos (Weight Vector): cada capa de una red neuronal está compuesta por una matriz de pesos y un vector de sesgo. Cada fila (o columna) de la matriz de pesos puede verse como un vector que representa los pesos de un neurona específica.
• Vector de incrustación (Embedding Vector): se utiliza para representar palabras, usuarios, elementos, etc., en espacios vectoriales de baja dimensión. Word2Vec, GloVe, BERT son técnicas de incrustación típicas que representan palabras como vectores.
• Espacio latente (Latent Space): los autoencoder, los autoencoder variacionales (Variational Autoencoder, VAE) y las redes generativas adversarias (Generative Adversarial Network, GAN) aprenden métodos para mapear datos a un espacio latente de baja dimensión. Este espacio latente también puede verse como un espacio vectorial.

Haga clic para ver el contenido (análisis detallado: normas y distancias - perspectiva del aprendizaje profundo)

Normas y Distancias en el Aprendizaje Profundo

Medir el tamaño (magnitude) de un vector o la distancia entre dos vectores es muy importante en el aprendizaje profundo. Se utiliza en diversas áreas, como funciones de pérdida, regularización, medición de similitud, etc.

Norma (Norm)

La Lp-norm de un vector \(\mathbf{x} = [x_1, x_2, ..., x_n]\) se define como sigue (\(p \ge 1\)).

\(||\mathbf{x}||_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{1/p}\)

• L1-norm (\(p=1\)): \(||\mathbf{x}||_1 = \sum_{i=1}^{n} |x_i|\) (distancia de Manhattan, norma del taxi)
  • Características: suma de los valores absolutos de cada elemento. Útil cuando la magnitud de cada elemento del vector de características es importante.
  • Uso en aprendizaje profundo: La regularización L1 (regresión Lasso) se utiliza para crear modelos escasos (algunos pesos son 0) al limitar la suma de los valores absolutos de los pesos.
• L2-norm (\(p=2\)): \(||\mathbf{x}||_2 = \sqrt{\sum_{i=1}^{n} x_i^2}\) (norma euclidiana)
  • Características: distancia en línea recta desde el origen hasta las coordenadas del vector (teorema de Pitágoras). Es la norma más comúnmente utilizada.
  • Uso en aprendizaje profundo: La regularización L2 (regresión Ridge) se utiliza para prevenir que los pesos sean demasiado grandes (previniendo el sobreajuste, overfitting). También se conoce como atenuación de pesos (weight decay).
• L∞-norm (\(p \to \infty\)): \(||\mathbf{x}||_\infty = \max_i |x_i|\)
  • Características: el valor absoluto más grande entre los elementos del vector.
  • Uso en aprendizaje profundo: (menos común) se utiliza para limitar que ciertos elementos sean demasiado grandes.

Distancia (Distance)

La distancia entre dos vectores \(\mathbf{x}\) y \(\mathbf{y}\) generalmente se define como la norma de su diferencia.

\(d(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||\)

• L1 distancia: \(d(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||_1 = \sum_{i=1}^{n} |x_i - y_i|\)
• L2 distancia: \(d(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||_2 = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}\)

Ejemplos de uso en aprendizaje profundo:

• Funciones de pérdida: MSE (L2 Loss), MAE (L1 Loss)
• Regularización: regularización L1, regularización L2 (atenuación de pesos, weight decay)
• Aprendizaje basado en similitud/distancia: k-NN, SVM, Red Siamesa, Red Triplet, Aprendizaje Contrastivo
• Embeddings: representar palabras, usuarios, ítems, etc., en un espacio vectorial y determinar su similitud/relación a través de la distancia entre vectores.
• Detección de anomalías (Outlier Detection): detectar anomalías basándose en las distancias entre puntos de datos.

Referencia: En el aprendizaje profundo, es importante distinguir entre “distancia” y “similitud”. La distancia es menor cuando la similitud es mayor, y la similitud es mayor cuando los valores son más cercanos. La similitud coseno (cosine similarity) es uno de los métodos de medición de similitud más comúnmente utilizados en el aprendizaje profundo.

Haga clic para ver el contenido (análisis detallado: espacio afín)

Espacio afín (Affine Space)

El espacio afín es una generalización del concepto de espacio vectorial en álgebra lineal, y es una herramienta útil para entender los modelos de aprendizaje profundo desde un punto de vista geométrico. En particular, la transformación afín representa la forma de agregar un sesgo (bias) a las transformaciones lineales que se utilizan comúnmente en el aprendizaje profundo.

Definición del espacio afín

Un espacio afín es una estructura compuesta por tres elementos: (conjunto de puntos, espacio vectorial, adición de punto y vector). Más específicamente,

• Conjunto de puntos (\(\mathcal{A}\)): Conjunto de objetos geométricos (puntos). A diferencia del espacio vectorial, no tiene un origen fijo.
• Espacio vectorial (\(V\)): Conjunto de vectores que representan el desplazamiento o la diferencia entre puntos. Satisface todas las propiedades del espacio vectorial (adición, producto escalar, 8 axiomas).
• Adición de punto y vector (\(\mathcal{A} \times V \to \mathcal{A}\)): Operación que suma un punto \(P \in \mathcal{A}\) con un vector \(\mathbf{v} \in V\) para obtener un nuevo punto \(Q \in \mathcal{A}\). Se denota como \(Q = P + \mathbf{v}\).

Esta operación de adición debe satisfacer las siguientes dos propiedades:

1. Para cualquier punto \(P \in \mathcal{A}\), \(P + \mathbf{0} = P\) (donde \(\mathbf{0}\) es el vector cero del espacio vectorial \(V\))
2. Para cualquier punto \(P, Q, R \in \mathcal{A}\), \((P + \mathbf{u}) + \mathbf{v} = P + (\mathbf{u} + \mathbf{v})\) (donde \(\mathbf{u}, \mathbf{v} \in V\))

Características importantes

• En el espacio afín, no existe un punto “origen” especial. Todos los puntos son equivalentes.
• La “diferencia” entre dos puntos \(P, Q \in \mathcal{A}\) se expresa como un vector del espacio vectorial \(V\): \(\overrightarrow{PQ} = Q - P \in V\). (Sin embargo, la “suma” de dos puntos no está definida.)
• A través de la adición de punto y vector, es posible moverse de un punto a otro.

Combinación afín

Dado un conjunto de puntos \(P_1, P_2, ..., P_k\) en el espacio afín \(\mathcal{A}\) y escalares \(c_1, c_2, ..., c_k\), una combinación afín tiene la siguiente forma:

\(c_1P_1 + c_2P_2 + ... + c_kP_k\) (con la condición de que \(c_1 + c_2 + ... + c_k = 1\))

Importante: A diferencia de las combinaciones lineales, en una combinación afín la suma de los coeficientes debe ser 1. Esta condición refleja la propiedad del espacio afín de que “no tiene un origen”.

Transformación afín

Una transformación afín es una función del espacio afín al espacio afín, que se puede expresar como una combinación de una transformación lineal y una traslación. Es decir, una transformación afín incluye tanto una transformación lineal como un sesgo (bias).

\(f(P) = T(P) + \mathbf{b}\)

• \(T\): Transformación lineal (transformación lineal del espacio vectorial \(V\) a sí mismo)
• \(\mathbf{b}\): Vector de traslación (elemento del espacio vectorial \(V\))

Representación matricial:

Una transformación afín se puede representar utilizando una matriz aumentada. En un espacio afín de \(n\) dimensiones, se utiliza un vector de \(n+1\) dimensiones para representar la transformación afín como una matriz \((n+1) \times (n+1)\). \(\begin{bmatrix} \mathbf{y} \\ 1 \end{bmatrix} = \begin{bmatrix} \mathbf{A} & \mathbf{b} \\ \mathbf{0}^T & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix}\)

• \(\mathbf{A}\): matriz de transformación lineal \(n \times n\)
• \(\mathbf{b}\): vector de traslación \(n\)-dimensional
• \(\mathbf{x}\): vector de entrada \(n\)-dimensional (punto en el espacio afín)
• \(\mathbf{y}\): vector de salida \(n\)-dimensional (punto en el espacio afín)

Espacio afín y transformación afín en el aprendizaje profundo

• Capa completamente conectada: la capa fully connected (capa densa) del aprendizaje profundo realiza una transformación afín. En \(\mathbf{y} = \mathbf{W}\mathbf{x} + \mathbf{b}\), \(\mathbf{W}\mathbf{x}\) representa la transformación lineal y \(\mathbf{b}\) el sesgo (traslación).
• Espacio de entrada: los datos de entrada del modelo de aprendizaje profundo a menudo se representan como vectores de alta dimensión, pero en sentido estricto, pueden considerarse puntos en un espacio afín sin origen. Por ejemplo, los datos de imagen se representan como vectores con los valores de brillo de cada píxel, pero este espacio vectorial no tiene un origen especial.
• Espacio de características (Feature Space): cada capa de la red neuronal transforma las entradas a un nuevo espacio de características. Estas transformaciones suelen consistir en una combinación de transformaciones afines (transformación lineal + sesgo) y funciones de activación no lineales.
• Aumento de datos (Data Augmentation): las rotaciones, traslaciones y ajustes de escala de los datos de imagen se pueden representar como transformaciones afines.
• Capa Afín: a diferencia de la transformación lineal, considera el sesgo.

Modelos de aprendizaje profundo sin sesgo

En investigaciones recientes en aprendizaje profundo, se han propuesto modelos que eliminan los términos de sesgo (bias) para mejorar la eficiencia computacional, la interpretabilidad del modelo o basándose en ciertos marcos teóricos.

• MuZero de DeepMind (2020): el modelo de aprendizaje por refuerzo MuZero no utiliza sesgo en sus redes policy y value. El paper menciona que eliminar el sesgo ayuda al aprendizaje de representaciones.
• Serie GPT (Generative Pre-trained Transformer) de OpenAI: en algunas investigaciones y implementaciones, se eliminan los términos de sesgo por eficiencia computacional. Sin embargo, no todos los modelos de la serie GPT omiten el sesgo. Modelos a gran escala como GPT-3 siguen utilizando sesgo en muchos casos.
• Redes sin Sesgo: algunos estudios analizan sistemáticamente el impacto de eliminar el sesgo en el rendimiento de generalización del modelo.

Razones para eliminar el sesgo

• Eficiencia computacional: al eliminar el término de sesgo, se reduce el número de parámetros del modelo, lo que disminuye la cantidad de cálculos y uso de memoria. Este efecto puede ser más significativo en modelos a gran escala.
• Aprendizaje de representaciones (Representation Learning): en ciertos problemas, el término de sesgo puede ser innecesario o incluso perjudicial para el aprendizaje de representaciones. Por ejemplo, en MuZero, se cree que las representaciones sin sesgo son más abstractas y generalizadas.
• Fundamento teórico/matemático: en algunos modelos (por ejemplo, ciertos tipos de modelos generativos), la ausencia de términos de sesgo puede ser matemáticamente más natural o más adecuada para ciertos análisis teóricos.
• Efecto regularizador: se ha encontrado que sin el sesgo, la matriz de pesos puede contener información más relevante, lo que actúa como un efecto regularizador. Nota: Eliminar el bias no siempre garantiza una mejora en el rendimiento. El impacto del bias en el rendimiento puede variar según las características del problema, la estructura del modelo, la cantidad de datos, entre otros factores.

El concepto de espacio afín y transformación afín puede ser utilizado en la interpretación geométrica de los modelos de aprendizaje profundo, en el análisis del rendimiento de generalización y en el diseño de nuevas arquitecturas.

2.1.2 Dimensiones, Rango

Los términos relacionados con tensores, vectores y matrices se utilizan de manera ligeramente diferente en las áreas de matemáticas, física y ciencias de la computación, lo que puede causar confusión. Para evitar esta confusión, revisemos los conceptos principales. Primero, examinaremos el rango y las dimensiones de un tensor. El rango de un tensor se refiere al número de índices que tiene el tensor. Por ejemplo, un escalar es un tensor de rango 0, un vector es un tensor de rango 1, una matriz es un tensor de rango 2. Los tensores de tres o más dimensiones generalmente se denominan simplemente tensores.

El término “dimensión” puede tener dos significados diferentes y requiere atención. En primer lugar, a veces se usa en el mismo sentido que el rango del tensor. En este caso, un vector se llama tensor de una dimensión, y una matriz se llama tensor de dos dimensiones. En segundo lugar, también se puede usar para indicar la longitud o tamaño de un arreglo. Por ejemplo, cuando decimos que las dimensiones del vector \(\mathbf{a} = [1, 2, 3, 4]\) son 4, nos referimos a esto.

Es importante conocer las diferencias en el uso de los términos según el campo. En física, el número de elementos tiene un significado físico, por lo que tiende a usarse más estrictamente. Por otro lado, en ciencias de la computación, se tratan los vectores, matrices y tensores principalmente como arreglos de números, y el término “dimensión” se usa indistintamente para referirse tanto al número de datos como al número de índices.

Para evitar confusiones debido a estas diferencias en el uso de términos, hay algunos puntos que deben tenerse en cuenta. El significado de los términos puede variar según el contexto y debe interpretarse con cuidado. Es necesario distinguir claramente cómo se usa “dimensión” en un artículo o libro. En particular, en el campo del aprendizaje profundo, a menudo se utiliza “dimensión” para referirse tanto al rango del tensor como al tamaño de la matriz, por lo que una interpretación coherente es importante.

En los marcos de aprendizaje profundo, los términos ‘dimensión’ o ‘eje’ se utilizan para describir la forma (shape) de un tensor. Por ejemplo, en PyTorch, se puede verificar el tamaño de cada dimensión del tensor mediante tensor.shape o tensor.size(). En este libro, el rango de un tensor (rank) se denominará ‘dimensión’, y la longitud/tamaño del arreglo se expresará como los valores de los elementos de shape o como dimensiones.

2.1.3 Fundamentos de la transformación lineal

Vamos a revisar las matemáticas necesarias para el entrenamiento de deep learning. La transformación lineal, que es una operación central en las redes neuronales, se expresa muy simplemente en el cálculo forward. En esta sección nos centraremos en las operaciones lineales básicas antes de pasar por la función de activación.

La forma básica del cálculo forward es la siguiente.

\[\boldsymbol y = \boldsymbol x \boldsymbol W + \boldsymbol b\]

Aquí, \(\boldsymbol x\) es la entrada, \(\boldsymbol W\) son los pesos, \(\boldsymbol b\) es el sesgo, y \(\boldsymbol y\) es la salida. En las matemáticas de las redes neuronales, las entradas y salidas a menudo se representan como vectores, mientras que los pesos se representan como matrices. El sesgo (\(\boldsymbol b\)) puede representarse a veces como un valor escalar, pero técnicamente debe ser un vector del mismo tamaño que la salida.

Matrices y transformaciones lineales

Las matrices son una herramienta poderosa para representar transformaciones lineales. Una transformación lineal es un proceso que mapea un punto en el espacio de vectores a otro punto, lo cual se puede ver como una deformación del espacio completo. Para comprender este concepto visualmente, recomiendo el video “Linear transformations and matrices” de 3Blue1Brown[1]. Este video explica de manera intuitiva los conceptos básicos del álgebra lineal y muestra claramente cómo las matrices deforman el espacio.

Cuando la entrada de datos \(\boldsymbol x\) se representa como un vector, esto significa un solo punto de datos y la longitud del vector es igual al número de características. Sin embargo, en el proceso de entrenamiento real, generalmente se procesan múltiples datos a la vez. En este caso, la entrada es una matriz \(\boldsymbol X\) de forma (n, m), donde n es el número de datos y m es el número de características.

En modelos de deep learning reales, los datos de entrada pueden tener formas tensoriales de más alta dimensión que las matrices bidimensionales.

• Datos de imágenes: un tensor de 4 dimensiones con la forma (tamaño del lote, altura, anchura, canales)
• Datos de video: un tensor de 5 dimensiones con la forma (tamaño del lote, número de frames, altura, anchura, canales)

Las redes neuronales utilizan varias formas de transformaciones lineales y no lineales para procesar estos datos de alta dimensión. El proceso de retropropagación en las transformaciones lineales implica calcular los gradientes y pasarlos hacia atrás a través de cada capa para actualizar los parámetros. Aunque este proceso puede ser complejo, se realiza eficientemente con herramientas de diferenciación automática. Aunque la transformación lineal es un componente fundamental de los modelos de deep learning, el rendimiento real de estos modelos se obtiene a través de la combinación con funciones de activación no lineales. En la próxima sección, examinaremos cómo esta no linealidad aumenta la capacidad de representación del modelo.

# if in Colab, plase don't run this and below code. just see the result video bleow the following cell.
#from manim import *  

%%manim -qh -v WARNING LinearTransformations  
from manim import *
from manim import config

class LinearTransformations(ThreeDScene):
    def construct(self):
        self.set_camera_orientation(phi=75 * DEGREES, theta=-45 * DEGREES)
        axes = ThreeDAxes(x_range=[-6, 6, 1], y_range=[-6, 6, 1], z_range=[-6, 6, 1], x_length=10, y_length=10, z_length=10).set_color(GRAY)
        self.add(axes)

        # --- 3D Linear Transformation (Rotation and Shear) ---
        title = Text("3D Linear Transformations", color=BLACK).to_edge(UP)
        self.play(Write(title))
        self.wait(1)

        # 1. Rotation around Z-axis
        text_rotation = Text("Rotation around Z-axis", color=BLUE).scale(0.7).next_to(title, DOWN, buff=0.5)
        self.play(Write(text_rotation))
        cube = Cube(side_length=2, fill_color=BLUE, fill_opacity=0.5, stroke_color=WHITE, stroke_width=1)
        self.play(Create(cube))
        self.play(Rotate(cube, angle=PI/2, axis=OUT, about_point=ORIGIN), run_time=2)
        self.wait(1)
        self.play(FadeOut(text_rotation))

        # 2. Shear
        text_shear = Text("Shear Transformation", color=GREEN).scale(0.7).next_to(title, DOWN, buff=0.5)
        self.play(Write(text_shear))

        # Define the shear transformation matrix.  This shears in x relative to y, and in y relative to x.
        shear_matrix = np.array([
            [1, 0.5, 0],
            [0.5, 1, 0],
            [0, 0, 1]
        ])

        self.play(
            cube.animate.apply_matrix(shear_matrix),
            run_time=2,
        )
        self.wait(1)

        # Add transformed axes to visualize the shear
        transformed_axes = axes.copy().apply_matrix(shear_matrix)
        self.play(Create(transformed_axes), run_time=1)
        self.wait(1)

        self.play(FadeOut(cube), FadeOut(transformed_axes), FadeOut(text_shear))

        # --- 2D to 3D Transformation (Paraboloid) ---
        text_2d_to_3d = Text("2D to 3D: Paraboloid", color=MAROON).scale(0.7).next_to(title, DOWN, buff=0.5)
        self.play(Write(text_2d_to_3d))

        square = Square(side_length=4, fill_color=MAROON, fill_opacity=0.5, stroke_color=WHITE, stroke_width=1)
        self.play(Create(square))

        def paraboloid(point):  # Function for the transformation
            x, y, _ = point
            return [x, y, 0.2 * (x**2 + y**2)]  # Adjust scaling factor (0.2) as needed

        paraboloid_surface = always_redraw(lambda: Surface(
            lambda u, v: axes.c2p(*paraboloid(axes.p2c(np.array([u,v,0])))),
            u_range=[-2, 2],
            v_range=[-2, 2],
            resolution=(15, 15), # Added for smoothness
            fill_color=MAROON,
            fill_opacity=0.7,
            stroke_color=WHITE,
            stroke_width=0.5

        ).set_shade_in_3d(True))


        self.play(
            Transform(square, paraboloid_surface),
            run_time=3,
        )

        self.wait(2)
        self.play(FadeOut(square), FadeOut(text_2d_to_3d))

        # --- 3D to 2D Transformation (Projection) ---
        text_3d_to_2d = Text("3D to 2D: Projection", color=PURPLE).scale(0.7).next_to(title, DOWN, buff=0.5)
        self.play(Write(text_3d_to_2d))

        sphere = Sphere(radius=1.5, fill_color=PURPLE, fill_opacity=0.7, stroke_color=WHITE, stroke_width=1, resolution=(20,20)).set_shade_in_3d(True)
        self.play(Create(sphere))


        def project_to_2d(mob, alpha):
            for p in mob.points:
                p[2] *= (1-alpha)

        self.play(
            UpdateFromAlphaFunc(sphere, project_to_2d),
            run_time=2
        )

        self.wait(1)

        # Show a circle representing the final projection 
        circle = Circle(radius=1.5, color=PURPLE, fill_opacity=0.7, stroke_color = WHITE, stroke_width=1)
        self.add(circle)
        self.wait(1)

        self.play(FadeOut(sphere), FadeOut(text_3d_to_2d), FadeOut(circle), FadeOut(title))

        self.wait(1)

import logging
logging.getLogger("manim").setLevel(logging.WARNING)

if __name__ == "__main__":
    config.video_dir = "./"
    scene = LinearTransformations()
    scene.render()

2.1.4 Operaciones de tensores

Desafío: ¿Cómo se pueden expresar y operar eficientemente los datos multidimensionales?

Lucha del investigador: Al principio del aprendizaje profundo, los investigadores tuvieron que manejar diferentes tipos de datos, como imágenes, texto, audio, entre otros. Estos datos eran difíciles de representar con vectores o matrices simples y se necesitaba un método para procesar eficazmente estructuras de datos complejas. Además, era una tarea importante encontrar formas eficientes de procesar rápidamente grandes volúmenes de datos.

Los tensores son los objetos matemáticos básicos utilizados en el aprendizaje profundo para representar datos y parámetros del modelo. Son un concepto generalizado que incluye escalares, vectores y matrices, y pueden pensarse como arreglos multidimensionales. Los tensores se clasifican según su dimensión (dimensión, rango) de la siguiente manera:

• 0D tensor: escalar (ejemplo: 3.14)
• 1D tensor: vector (ejemplo: [1, 2, 3])
• 2D tensor: matriz (ejemplo: [[1, 2], [3, 4]])
• 3D o más: tensores de alta dimensión

En el aprendizaje profundo, se manejan principalmente los siguientes tipos de tensores:

• Datos de entrada:
  • General: (tamaño del lote, número de características)
  • Secuencia/texto: (tamaño del lote, longitud de la secuencia, número de características/dimensión de incrustación)
  • Imagenes: (tamaño del lote, altura, ancho, canales)
• Pesos (Weights):
  • Conexiones completas (Fully-connected): (número de características de entrada, número de características de salida)
  • Convolutivas (Convolutional): (número de canales de salida, número de canales de entrada, altura del kernel, ancho del kernel)
• Datos de salida (Output/Prediction):
  • Clasificación (Classification): (tamaño del lote, número de clases)
  • Regresión (Regression): (tamaño del lote, dimensión de salida)
• Sesgo (Bias):
  • Conexiones completas: (número de características de salida,)
  • Convolutivas: (número de canales de salida,)
• Mapas de características (salida de capas convolucionales): (tamaño del lote, número de canales de salida, altura, ancho)

La transformación lineal básica en una red neuronal es la siguiente.

\(y_j = \sum\limits_{i} x_i w_{ij} + b_j\)

Aquí, \(i\) es el índice de entrada y \(j\) es el índice de salida. Esto se puede expresar en forma de vector y matriz de la siguiente manera.

\(\boldsymbol x = \begin{bmatrix}x_{1} & x_{2} & \cdots & x_{i} \end{bmatrix}\)

\(\boldsymbol W = \begin{bmatrix} w_{11} & \cdots & w_{1j} \ \vdots & \ddots & \vdots \ w_{i1} & \cdots & w_{ij} \end{bmatrix}\)

\(\boldsymbol y = \boldsymbol x \boldsymbol W + \boldsymbol b\)

Las principales características de las operaciones de tensores son:

1. Broadcasting: Permite realizar operaciones entre tensores de diferentes tamaños.

2. Reducción de dimensiones: Se pueden reducir dimensiones específicas de un tensor usando operaciones como sum(), mean(), etc.

3. Reshape (reformado): Permite cambiar la forma del tensor para convertirlo en un tensor de otras dimensiones.

Una de las operaciones más importantes en el aprendizaje de redes neuronales es el cálculo de gradientes. Los principales cálculos de gradientes son:

1. Gradiente con respecto a la entrada: \(\frac{\partial \boldsymbol y}{\partial \boldsymbol{x}}\)

2. Gradiente con respecto a los pesos: \(\frac{\partial \boldsymbol y}{\partial \boldsymbol W}\)

Estos gradientes representan el cambio en la salida debido al cambio en las entradas y los pesos, respectivamente, y son fundamentales para el algoritmo de retropropagación. Las operaciones de tensor son fundamentales en el aprendizaje profundo moderno, y permiten un procesamiento paralelo avanzado mediante el uso de GPU, facilitando así el entrenamiento eficiente y la inferencia de modelos a gran escala. Además, la diferenciación automática (automatic differentiation) de las operaciones de tensor posibilita cálculos de gradiente eficientes, convirtiéndose en un punto de inflexión crucial en la investigación moderna de aprendizaje profundo. Esto va más allá de simples cálculos numéricos y transforma la estructura del modelo y el propio proceso de aprendizaje en objetos programables. Veremos ejemplos prácticos de operaciones de tensor en el Capítulo 3 sobre PyTorch.

1. Centrado de datos (Data Centering): Se asegura de que la media de cada característica (feature) sea 0.
2. Cálculo de la matriz de covarianza: Se calcula la matriz de covarianza, que representa las correlaciones entre las características.
3. Descomposición en valores propios: Se calculan los valores propios (eigenvalue) y vectores propios (eigenvector) de la matriz de covarianza.
   • Vectores propios: dirección de los componentes principales
   • Valores propios: magnitud de la varianza en la dirección del componente principal correspondiente
4. Selección de componentes principales: Se seleccionan \(k\) vectores propios, comenzando desde el que tiene el mayor valor propio. (reducción a un espacio de \(k\) dimensiones)
5. Proyección de datos: Los datos se proyectan sobre los \(k\) componentes principales seleccionados para reducir la dimensionalidad.

Uso en el aprendizaje profundo:

• Preprocesamiento de datos: Al proyectar datos de alta dimensión, como imágenes o texto, a un espacio de baja dimensión y usarlos como entrada para modelos de aprendizaje profundo, se puede reducir el costo computacional y prevenir el sobreajuste. En particular, al representar imágenes de alta resolución en dimensiones más bajas mediante PCA, se puede aumentar la velocidad de entrenamiento del modelo.
• Extracción de características: Los componentes principales extraídos a través de PCA pueden interpretarse como nuevas características (features) que son independientes entre sí y preservan la máxima varianza en los datos.

SVD vs. PCA

• SVD es una técnica de descomposición de matrices, mientras que PCA es una técnica de reducción de dimensionalidad de los datos.
• PCA puede implementarse utilizando SVD (la descomposición en valores singulares de la matriz de datos está relacionada con la descomposición en valores propios de la matriz de covarianza).
• PCA requiere un preprocesamiento para ajustar la media de los datos a 0, mientras que SVD puede aplicarse directamente sin este proceso.

SVD y PCA son herramientas matemáticas importantes que juegan un papel crucial en el aprendizaje profundo para representar eficientemente los datos y mejorar el rendimiento del modelo.

from dldna.chapter_02.pca import visualize_pca
visualize_pca()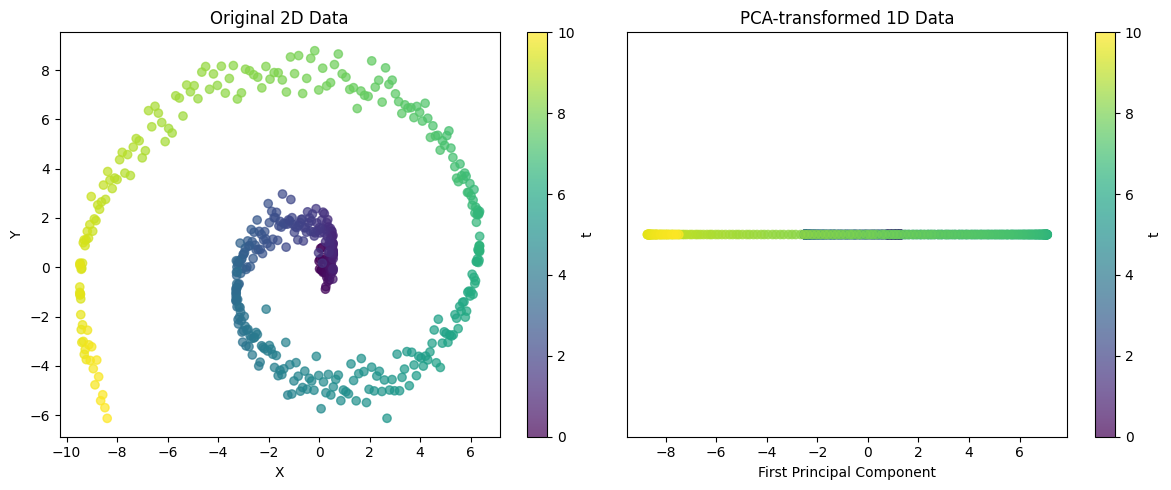

Explained variance ratio: 0.5705

Este ejemplo muestra la capacidad de PCA para proyectar estructuras 2D complejas a una dimensión. En el caso de datos espirales, un solo componente principal no puede capturar toda la variabilidad, pero puede capturar la tendencia principal de los datos. A través de la proporción de varianza explicada, se puede evaluar qué tan bien esta representación unidimensional preserva la estructura de los datos originales.

Estas técnicas son herramientas poderosas para extraer patrones importantes de datos complejos.

1. Preprocesamiento de datos: reducción de dimensionalidad de los datos de entrada
2. Compresión del modelo: aproximación eficiente de la matriz de pesos
3. Extracción de características: identificación y selección de características importantes

SVD y PCA son herramientas poderosas para extraer patrones importantes de datos de alta dimensión y simplificar estructuras de datos complejas.

2.2 Cálculo y optimización

2.2.1 Regla de la cadena

Desafío: ¿Cómo se pueden calcular eficientemente las derivadas de funciones complejas y anidadas?

Dilema del investigador: Los primeros investigadores en aprendizaje profundo tenían que utilizar el algoritmo de retropropagación para actualizar los pesos de las redes neuronales. Sin embargo, las redes neuronales son estructuras en las que varias capas de funciones están conectadas de manera compleja, por lo que calcular la derivada de la función de pérdida con respecto a cada peso era un problema muy difícil. En particular, a medida que aumentaba el número de capas, la cantidad de cálculos crecía exponencialmente, haciendo que el aprendizaje fuera ineficiente.

La regla de la cadena es una de las reglas de cálculo más importantes utilizadas en el aprendizaje profundo. La regla de la cadena es una regla poderosa y elegante que permite expresar la derivada de una función compuesta como el producto de las derivadas de las funciones componentes. Visualizar la regla de la cadena puede facilitar la comprensión del concepto. Por ejemplo, supongamos que \(z\) es una función de \(x\) y \(y\), y que \(x\) y \(y\) son a su vez funciones de \(s\) y \(t\). Esta relación se puede representar mediante un diagrama de árbol.

Regla de la cadena

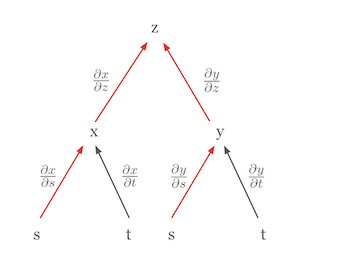
En este diagrama, la derivada parcial de \(z\) con respecto a \(s\), \(\frac{\partial z}{\partial s}\), es igual a la suma de los productos de las derivadas parciales a lo largo de todas las rutas desde \(z\) hasta \(s\).

\(\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial s}\)

En esta fórmula,

• \(\frac{\partial z}{\partial x}\) y \(\frac{\partial z}{\partial y}\) representan cómo \(z\) cambia con respecto a \(x\) y \(y\), respectivamente.
• \(\frac{\partial x}{\partial s}\) y \(\frac{\partial y}{\partial s}\) representan cómo \(x\) y \(y\) cambian con respecto a \(s\), respectivamente.

Consideremos otro caso donde la regla de la cadena se utiliza para expresar una diferencial total. Consideremos el caso en que \(z\) es una función de variables independientes. En este caso, la regla de la cadena se simplifica a la forma de una diferencial total. Por ejemplo, si \(z = f(x, y)\) con \(x = g(s)\) y \(y = h(t)\), y si \(s\) y \(t\) son independientes entre sí, entonces la diferencial total de \(z\) se puede expresar como sigue.

Regla de la cadena

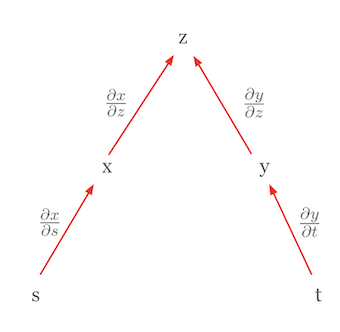
\(dz = \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy\)

Aquí, \(dx = \frac{\partial x}{\partial s}ds\) y \(dy = \frac{\partial y}{\partial t}dt\), por lo que finalmente se obtiene la siguiente forma.

\(dz = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s}ds + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}dt\)

Esta ecuación tiene una forma similar a la de la regla de la cadena, pero en realidad representa una diferencial total. Un punto importante aquí es que \(s\) y \(t\) son independientes, por lo que \(\frac{\partial x}{\partial t}\) y \(\frac{\partial y}{\partial s}\) son 0. Esta forma es una diferencial total. La diferencial total representa el impacto total del cambio en todas las variables independientes sobre el valor de la función, expresada como la suma de las derivadas parciales con respecto a cada variable. La estructura de la regla de la cadena permite descomponer la derivada de una función compleja en partes más simples. Esto es especialmente importante en el aprendizaje profundo, ya que las redes neuronales tienen una estructura compuesta por múltiples capas de funciones superpuestas. El uso de diagramas de árbol facilita la aplicación de la regla de la cadena incluso en situaciones más complejas. Se trata de encontrar todas las rutas desde la variable dependiente hasta las variables independientes a través de las variables intermedias, multiplicar las derivadas parciales a lo largo de cada ruta y sumar todos estos resultados.

La regla de la cadena es la base matemática del algoritmo de retropropagación en el aprendizaje profundo. Proporciona los fundamentos para actualizar eficientemente los pesos en modelos de redes neuronales complejas.

2.2.2 Gradiente y Jacobiano

Desafío: ¿Cómo se pueden generalizar las derivadas para funciones con diferentes formas de entrada y salida?

Reflexión del investigador: En sus inicios, el aprendizaje profundo se centró principalmente en funciones escalares, pero gradualmente comenzó a abordar funciones con entradas y salidas de diferentes formas, como vectores y matrices. Expresar y calcular las derivadas de estas funciones de manera uniforme fue una tarea esencial en el desarrollo de marcos de aprendizaje profundo.

En el aprendizaje profundo se tratan funciones con diferentes formas de entrada (escalares, vectores, matrices, tensores) y salida (escalares, vectores, matrices, tensores). En consecuencia, la representación de las derivadas (o gradientes) de estas funciones también varía. La clave es expresar coherentemente las derivadas en estos diferentes casos y aplicar la regla de la cadena para calcularlas de manera eficiente.

Conceptos clave

• Gradiente (Gradient): Expresión utilizada al diferenciar una función escalar con respecto a un vector. Es un vector columna que contiene las derivadas parciales de la función con respecto a cada elemento del vector de entrada. Indica la dirección de mayor ascenso de la función.

• Matriz Jacobiana (Jacobian Matrix): Expresión utilizada al diferenciar una función vectorial con respecto a un vector. Es una matriz que contiene las derivadas parciales de cada elemento del vector de salida con respecto a cada elemento del vector de entrada.

Representación de derivadas según diferentes formas de entrada y salida

Forma de entrada	Forma de salida	Representación de la derivada	Dimensiones
Vector (\(\mathbf{x}\))	Vector (\(\mathbf{f}\))	Matriz Jacobiana (\(\mathbf{J} = \frac{\partial \mathbf{f}}{\partial \mathbf{x}}\))	\(n \times m\)
Matriz (\(\mathbf{X}\))	Vector (\(\mathbf{f}\))	Tensor tridimensional (generalmente no se maneja bien)	-
Vector (\(\mathbf{x}\))	Matriz (\(\mathbf{F}\))	Tensor tridimensional (generalmente no se maneja bien)	-
Escalar (\(x\))	Vector (\(\mathbf{f}\))	Vector columna (\(\frac{\partial \mathbf{f}}{\partial x}\))	\(n \times 1\)
Vector (\(\mathbf{x}\))	Escalar (\(f\))	Gradiente (\(\nabla f = \frac{\partial f}{\partial \mathbf{x}}\))	\(m \times 1\) (vector columna)
Matriz (\(\mathbf{X}\))	Escalar (\(f\))	Matriz (\(\frac{\partial f}{\partial \mathbf{X}}\))	\(m \times n\)

Referencia:

• \(m\): dimensiones del vector/matriz de entrada, \(n\): dimensiones del vector/matriz de salida, \(p, q\): número de filas/columnas de la matriz
• En el caso de entradas matriciales y salidas vectoriales/matriciales, la derivada se convierte en un tensor tridimensional. Aunque los marcos de aprendizaje profundo manejan internamente estos cálculos de tensores de alta dimensión de manera eficiente, generalmente el cálculo de jacobianas y gradientes para entradas/salidas vectoriales/matriciales es lo más común.

Aplicación en Aprendizaje Profundo

• Algoritmo de Retropropagación: Las matrices jacobianas y los gradientes desempeñan un papel fundamental al implementar el algoritmo de retropropagación en aprendizaje profundo. Se aplica la regla de la cadena a través de cada capa de la red neuronal para calcular el gradiente de la función de pérdida con respecto a los pesos, y se utilizan estos gradientes para actualizar los pesos.
• Diferenciación Automática: Los marcos modernos de aprendizaje profundo (como TensorFlow, PyTorch, etc.) proporcionan funcionalidades de diferenciación automática (Automatic Differentiation) que manejan automáticamente estos cálculos complejos de derivadas. Los usuarios no necesitan implementar fórmulas de derivada complejas por sí mismos; solo deben definir la estructura del modelo y la función de pérdida.

De esta manera, los conceptos de gradientes y matrices jacobianas son herramientas esenciales en el aprendizaje profundo para generalizar la diferenciación de funciones de varias formas y aprender modelos de manera eficiente a través de la retropropagación.

Haz clic para ver el contenido (deep dive: matriz Hessiana)

Matriz Hessiana (Hessian Matrix)

1. Definición y significado de la matriz Hessiana

• Definición: La matriz Hessiana es una representación matricial de las derivadas parciales de segundo orden de una función escalar (scalar-valued function). Es decir, dada una función \(f(x_1, x_2, ..., x_n)\), la matriz Hessiana \(H\) se define como:

  \[ H = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \]

  • Cada elemento representa el valor de la segunda derivada parcial de la función con respecto a cada variable.
  • Matriz simétrica (Symmetric Matrix): Si las derivadas parciales de segundo orden son continuas, el orden en que se toman las derivadas parciales no importa (teorema de Schwarz), por lo que la matriz Hessiana es una matriz simétrica. (\(\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i}\))

• Significado:

  • Curvatura (Curvature): La matriz Hessiana contiene información sobre la curvatura local de la función. Indica cuánto se curva el gráfico de la función en un punto específico.
  • Tasa de cambio de la tasa de cambio: Mientras que las derivadas parciales de primer orden (gradiente, Gradient) indican la tasa de cambio de la función, la matriz Hessiana indica cuán rápidamente cambia esa tasa de cambio.

2. Uso de la matriz Hessiana para clasificar los puntos críticos (Critical Point)

• Punto crítico (Critical Point): Un punto donde la pendiente de la función (gradiente) es cero. Es decir, un punto donde todas las derivadas parciales de primer orden son cero. (\(\nabla f = 0\))
• Clasificación del punto crítico:
  • La matriz Hessiana se utiliza para determinar si un punto crítico es un máximo local (local maximum), un mínimo local (local minimum) o un punto de silla (saddle point).
  • Mínimo local (Local Minimum): Si la matriz Hessiana es una matriz definida positiva (positive definite), el punto crítico es un mínimo local. (Todos los valores propios son positivos)
  • Máximo local (Local Maximum): Si la matriz Hessiana es una matriz definida negativa (negative definite), el punto crítico es un máximo local. (Todos los valores propios son negativos)
  • Punto de silla (Saddle Point): Si la matriz Hessiana es una matriz indefinida (indefinite), el punto crítico es un punto de silla. (Tiene tanto valores propios positivos como negativos)
  • Semidefinida: Si la matriz Hessiana es positive/negative semidefinite, no se puede determinar el tipo de punto crítico sin información adicional. (Los valores propios incluyen cero)

3. Uso de la matriz Hessiana en el aprendizaje profundo (Deep Learning)

• Método de Newton:
  • Es uno de los algoritmos de optimización para encontrar los valores extremos de una función.
  • Mientras que el descenso por gradiente utiliza la derivada primera (gradiente), el método de Newton utiliza la derivada segunda (hessiana) para converger más rápidamente.
  • Regla de actualización: \(x_{k+1} = x_k - H^{-1}(x_k) \nabla f(x_k)\) (H es la matriz hessiana)
• Matriz de Curvatura:
  • La matriz hessiana puede ser utilizada como una matriz de curvatura para representar la curvatura de la función de pérdida.
  • Se utiliza la información de curvatura para ajustar la tasa de aprendizaje o mejorar el rendimiento del algoritmo de optimización. (por ejemplo, Descenso por Gradiente Natural)

2.2.3 Regla de la cadena y retropropagación en redes neuronales

El núcleo del aprendizaje de las redes neuronales es el algoritmo de retropropagación (Backpropagation). La retropropagación es un método eficiente para propagar el error que ocurre en la capa de salida hacia la capa de entrada, actualizando los pesos y sesgos de cada capa. En este proceso, la regla de la cadena (Chain Rule) permite expresar la derivada de funciones compuestas complejas como el producto de derivadas simples, lo que facilita los cálculos.

Aplicación de la regla de la cadena en redes neuronales

Las redes neuronales consisten en una composición de funciones en múltiples capas. Por ejemplo, una red neuronal de dos capas puede expresarse como sigue:

\(\mathbf{z} = f_1(\mathbf{x}; \mathbf{W_1}, \mathbf{b_1})\) \(\mathbf{y} = f_2(\mathbf{z}; \mathbf{W_2}, \mathbf{b_2})\)

Aquí, \(\mathbf{x}\) es la entrada, \(\mathbf{z}\) es la salida de la primera capa (entrada de la segunda capa), \(\mathbf{y}\) es la salida final, \(\mathbf{W_1}\), \(\mathbf{b_1}\) son los pesos y sesgos de la primera capa, \(\mathbf{W_2}\), \(\mathbf{b_2}\) son los pesos y sesgos de la segunda capa.

Durante el proceso de retropropagación, debemos calcular los gradientes del error \(E\) con respecto a cada parámetro (\(\frac{\partial E}{\partial \mathbf{W_1}}\), \(\frac{\partial E}{\partial \mathbf{b_1}}\), \(\frac{\partial E}{\partial \mathbf{W_2}}\), \(\frac{\partial E}{\partial \mathbf{b_2}}\)). Al aplicar la regla de la cadena, podemos realizar los cálculos como sigue:

\(\frac{\partial E}{\partial \mathbf{W_2}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{W_2}}\) \(\frac{\partial E}{\partial \mathbf{b_2}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{b_2}}\) \(\frac{\partial E}{\partial \mathbf{W_1}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{z}} \frac{\partial \mathbf{z}}{\partial \mathbf{W_1}}\) \(\frac{\partial E}{\partial \mathbf{b_1}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{z}} \frac{\partial \mathbf{z}}{\partial \mathbf{b_1}}\)

De esta manera, utilizando la regla de la cadena, podemos descomponer los gradientes de cada parámetro en una red neuronal compleja en productos de derivadas sucesivas y calcularlos eficientemente. La teoría detallada del proceso se explica en 2.2.4.

Gradientes y derivadas direccionales

• Gradiente (Gradient): Un vector que contiene las derivadas parciales (partial derivatives) de una función multivariable con respecto a cada variable. Indica la dirección de mayor pendiente de la función.
• Derivada direccional (Directional Derivative): Representa la tasa de cambio de la función en una dirección específica. Se puede calcular como el producto punto (dot product) del gradiente y el vector de dirección.

Puntos a tener en cuenta sobre la representación del gradiente

• Vector de columna vs. vector de fila: Generalmente, es convención representar los vectores como vectores de columna, pero en el aprendizaje profundo, también pueden representarse como vectores de fila según el contexto. Es importante mantener la consistencia. (Este libro utiliza la notación molecular.)
• Matriz jacobiana (Jacobian Matrix): Para funciones con múltiples variables de entrada y múltiples variables de salida (funciones vectoriales), es una matriz que contiene todos los valores de las derivadas parciales. Se usa en el cálculo del retropropagación en el aprendizaje profundo.

Basados en estos conceptos, en la siguiente sección examinaremos detalladamente el método de cálculo de gradientes durante el proceso de retropropagación, junto con ejemplos específicos.

2.2.4 Cálculo de gradientes para la propagación hacia atrás

El núcleo de la propagación hacia atrás es calcular los gradientes de la función de pérdida (Loss Function) para actualizar los pesos. Tomemos como ejemplo una transformación lineal simple (\(\mathbf{y} = \mathbf{xW} + \mathbf{b}\)) para examinar el proceso de propagación hacia atrás.

1. Idea central de la propagación hacia atrás

La propagación hacia atrás es un algoritmo que propaga el error calculado en la capa de salida hacia la capa de entrada, actualizando cada peso según su contribución al error. El cálculo de los gradientes de la función de pérdida con respecto a cada peso es fundamental en este proceso.

2. Gradiente de la función de pérdida

Si usamos el error cuadrático medio (Mean Squared Error, MSE) como función de pérdida, el gradiente de la función de pérdida \(E\) con respecto a la salida \(\mathbf{y}\) se expresa de la siguiente manera:

\(E = \frac{1}{M} \sum_{i=1}^{M} (y_i - \hat{y}_i)^2\)

\(\frac{\partial E}{\partial \mathbf{y}} = \frac{2}{M}(\mathbf{y} - \hat{\mathbf{y}})\)

Aquí, \(y_i\) es el valor real, \(\hat{y}_i\) es el valor predicho por el modelo, y \(M\) es el número de datos.

3. Gradiente con respecto a los pesos

Aplicando la regla de la cadena, podemos calcular el gradiente de la función de pérdida \(E\) con respecto a los pesos \(\mathbf{W}\):

\(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{W}}\)

Dado que \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), tenemos \(\frac{\partial \mathbf{y}}{\partial \mathbf{W}} = \mathbf{x}^T\).

Finalmente, el gradiente con respecto a los pesos se expresa de la siguiente manera:

\(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)

4. Gradiente con respecto a la entrada

El gradiente de la función de pérdida \(E\) con respecto a la entrada \(\mathbf{x}\) se utiliza para propagar el error hacia la capa anterior:

\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{x}}\)

Dado que \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), tenemos \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \mathbf{W}^T\).

Por lo tanto, el gradiente con respecto a la entrada es:

\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\)

5. Resumen

La propagación hacia atrás se realiza a través de los siguientes pasos clave. 1. Propagación hacia adelante (Forward Propagation): se pasa el dato de entrada \(\mathbf{x}\) a través de la red neuronal para calcular la predicción \(\hat{\mathbf{y}}\). 2. Cálculo de la función de pérdida: se compara la predicción \(\hat{\mathbf{y}}\) con el valor real \(\mathbf{y}\) para calcular la pérdida \(E\). 3. Propagación hacia atrás (Backward Propagation): * se calcula el gradiente de la función de pérdida respecto a la capa de salida \(\frac{\partial E}{\partial \mathbf{y}}\). * utilizando la regla de la cadena, se calcula el gradiente con respecto a los pesos \(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\). * se calcula el gradiente con respecto a las entradas \(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\) para propagar el error hacia la capa anterior. 4. Actualización de los pesos: se utilizan los gradientes calculados para actualizar los pesos mediante algoritmos de optimización como el descenso por gradiente.

El algoritmo de propagación hacia atrás es fundamental en el entrenamiento de modelos de aprendizaje profundo, permitiendo aproximar eficazmente funciones no lineales complejas.

Haz clic para ver el contenido (deep dive: cálculo de gradientes para retropropagación)

La clave de la retropropagación es calcular el gradiente de la función de pérdida (Loss Function) para actualizar los pesos. Tomemos como ejemplo una transformación lineal simple (\(\mathbf{y} = \mathbf{xW} + \mathbf{b}\)) y examinemos el proceso de retropropagación. Aquí explicamos el proceso de cálculo en detalle.

Gradiente de la función de pérdida

El objetivo del aprendizaje de redes neuronales es minimizar la función de pérdida \(E\). Cuando se utiliza el error cuadrático medio (MSE) como función de pérdida, esto se ve de la siguiente manera.

\(E = f(\mathbf{y}) = \frac{1}{M} \sum_{i=1}^{M} (y_i - \hat{y}_i)^2\)

Aquí, \(y_i\) es el valor real, \(\hat{y}_i\) es el valor predicho y \(M\) es el número de datos (o la dimensión del vector de salida).

La derivada de \(E\) con respecto a \(\mathbf{y}\) es:

\(\frac{\partial E}{\partial \mathbf{y}} = \frac{2}{M} (\mathbf{y} - \hat{\mathbf{y}})\)

Aquí, \(\mathbf{y}\) es el vector de salida de la red neuronal y \(\hat{\mathbf{y}}\) es el vector de valores reales (objetivos). Como \(y_i\) son constantes (cada elemento del objetivo), solo quedan las derivadas parciales con respecto a \(\mathbf{y}\).

Nota: En el código de ejemplo del Capítulo 1, se utilizó el término \(-\frac{2}{M}\). Esto fue debido a que la definición de la función de pérdida incluía un signo negativo (-). Aquí usamos la definición general de MSE, por lo que se utiliza el valor positivo \(\frac{2}{M}\). En el aprendizaje real, este constante se multiplica por la tasa de aprendizaje (learning rate), por lo que su magnitud absoluta no es crucial.

Gradiente de la función de pérdida con respecto a los pesos

Ahora, calculemos el gradiente de la función de pérdida \(E\) con respecto a los pesos \(\mathbf{W}\). Dado que \(E = f(\mathbf{y})\) y \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), donde \(\mathbf{x}\) es el vector de entrada, \(\mathbf{W}\) es la matriz de pesos y \(\mathbf{b}\) es el vector de sesgo.

Gráfico de cálculo:

Para visualizar el proceso de retropropagación, se puede usar un gráfico de cálculo. (Inserción de imagen del gráfico de cálculo)

\(E\) es un valor escalar y necesitamos calcular la derivada parcial de \(E\) con respecto a cada \(w_{ij}\) (cada elemento de la matriz de pesos \(\mathbf{W}\)). \(\mathbf{W}\) es una matriz de tamaño (dimensión de entrada) x (dimensión de salida). Por ejemplo, si la entrada tiene 3 dimensiones (\(x_1, x_2, x_3\)) y la salida tiene 2 dimensiones (\(y_1, y_2\)), entonces \(\mathbf{W}\) es una matriz de 3x2.

\(\frac{\partial E}{\partial \mathbf{W}} = \begin{bmatrix} \frac{\partial E}{\partial w_{11}} & \frac{\partial E}{\partial w_{12}} \\ \frac{\partial E}{\partial w_{21}} & \frac{\partial E}{\partial w_{22}} \\ \frac{\partial E}{\partial w_{31}} & \frac{\partial E}{\partial w_{32}} \end{bmatrix}\)

La derivada de \(E\) con respecto a \(\mathbf{y}\) puede expresarse como un vector fila: \(\frac{\partial E}{\partial \mathbf{y}} = \begin{bmatrix} \frac{\partial E}{\partial y_1} & \frac{\partial E}{\partial y_2} \end{bmatrix}\) (usando la notación de numerador). Técnicamente, el gradiente debe expresarse como un vector columna, pero aquí usamos un vector fila por conveniencia en los cálculos.

Por la regla de la cadena, \(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{W}}\)

\(\frac{\partial E}{\partial w_{ij}} = \sum_k \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial w_{ij}}\) (donde \(k\) es el índice del vector de salida \(\mathbf{y}\))

Desarrollando la ecuación anterior,

\(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial y_1} \frac{\partial y_1}{\partial \mathbf{W}} + \frac{\partial E}{\partial y_2} \frac{\partial y_2}{\partial \mathbf{W}}\)

Ahora debemos calcular \(\frac{\partial y_k}{\partial w_{ij}}\). Dado que \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\),

\(y_1 = x_1w_{11} + x_2w_{21} + x_3w_{31} + b_1\) \(y_2 = x_1w_{12} + x_2w_{22} + x_3w_{32} + b_2\)

\(\frac{\partial y_1}{\partial w_{ij}} = \begin{bmatrix} \frac{\partial y_1}{\partial w_{11}} & \frac{\partial y_1}{\partial w_{12}} \\ \frac{\partial y_1}{\partial w_{21}} & \frac{\partial y_1}{\partial w_{22}} \\ \frac{\partial y_1}{\partial w_{31}} & \frac{\partial y_1}{\partial w_{32}} \end{bmatrix} = \begin{bmatrix} x_1 & 0 \\ x_2 & 0 \\ x_3 & 0 \end{bmatrix}\)

\(\frac{\partial y_2}{\partial w_{ij}} = \begin{bmatrix} 0 & x_1 \\ 0 & x_2 \\ 0 & x_3 \end{bmatrix}\)

Por lo tanto,

\(\frac{\partial E}{\partial \mathbf{W}} = \frac{\partial E}{\partial y_1} \begin{bmatrix} x_1 & 0 \\ x_2 & 0 \\ x_3 & 0 \end{bmatrix} + \frac{\partial E}{\partial y_2} \begin{bmatrix} 0 & x_1 \\ 0 & x_2 \\ 0 & x_3 \end{bmatrix} = \begin{bmatrix} \frac{\partial E}{\partial y_1}x_1 & \frac{\partial E}{\partial y_2}x_1 \\ \frac{\partial E}{\partial y_1}x_2 & \frac{\partial E}{\partial y_2}x_2 \\ \frac{\partial E}{\partial y_1}x_3 & \frac{\partial E}{\partial y_2}x_3 \end{bmatrix} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \begin{bmatrix} \frac{\partial E}{\partial y_1} & \frac{\partial E}{\partial y_2} \end{bmatrix} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)

Generalización:

Cuando la entrada es un vector fila \(1 \times m\) \(\mathbf{x}\), y la salida es un vector fila \(1 \times n\) \(\mathbf{y}\), los pesos \(\mathbf{W}\) son una matriz \(m \times n\). En este caso, \(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)

Gradiente de la función de pérdida con respecto a la entrada

El gradiente de la función de pérdida \(E\) con respecto a la entrada \(\mathbf{x}\) también se puede calcular utilizando la regla de la cadena.

\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{x}}\)

Dado que \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), entonces \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \mathbf{W}^T\).

Por lo tanto,

\(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\)

Gradiente con respecto al sesgo

El gradiente de la función de pérdida con respecto al sesgo \(\mathbf{b}\) es el siguiente.

\(\frac{\partial E}{\partial \mathbf{b}} = \frac{\partial E}{\partial \mathbf{y}} \frac{\partial \mathbf{y}}{\partial \mathbf{b}}\)

Dado que \(\mathbf{y} = \mathbf{xW} + \mathbf{b}\), entonces \(\frac{\partial \mathbf{y}}{\partial \mathbf{b}} = \begin{bmatrix} 1 & 1 & \dots & 1\end{bmatrix}\) (un vector fila de \(1 \times n\) compuesto únicamente por unos).

\(\frac{\partial E}{\partial \mathbf{b}} = \frac{\partial E}{\partial \mathbf{y}}\)

Resumen y explicaciones adicionales

1. Gradiente con respecto a los pesos: \(\frac{\partial E}{\partial \mathbf{W}} = \mathbf{x}^T \frac{\partial E}{\partial \mathbf{y}}\)
   • Se calcula como el producto matricial del vector de entrada transpuesto \(\mathbf{x}\) y el gradiente de la función de pérdida con respecto a la salida (\(\frac{\partial E}{\partial \mathbf{y}}\), que se expresa como un vector fila).
2. Gradiente con respecto a la entrada: \(\frac{\partial E}{\partial \mathbf{x}} = \frac{\partial E}{\partial \mathbf{y}} \mathbf{W}^T\)
   • Se calcula como el producto matricial del gradiente de la función de pérdida con respecto a la salida (\(\frac{\partial E}{\partial \mathbf{y}}\)) y la matriz de pesos transpuesta \(\mathbf{W}\). Este resultado se retropropaga al capa anterior para actualizar los pesos de esa capa.
3. Gradiente con respecto al sesgo: \(\frac{\partial E}{\partial \mathbf{b}} = \frac{\partial E}{\partial \mathbf{y}}\)
   • Es igual al gradiente de la función de pérdida con respecto a la salida.
4. Uso del gradiente: Los gradientes calculados se utilizan en algoritmos de optimización como el descenso por gradiente (Gradient Descent) para actualizar los pesos y sesgos. Cada parámetro se actualiza en la dirección opuesta al gradiente para minimizar la función de pérdida.
5. Notación: En la descripción anterior, se utilizó la notación de numerador para calcular el gradiente. También se puede usar la notación de denominador, pero al final se obtendrá la misma regla de actualización. Lo importante es usar una notación consistente. Este libro utiliza la notación de numerador.

A través de este proceso matemático, los modelos de aprendizaje profundo pueden aprender transformaciones no lineales complejas de datos de entrada a datos de salida.

2.3 Probabilidad y estadística

El aprendizaje profundo se basa profundamente en la teoría de probabilidad y estadística para manejar la incertidumbre de los datos. En este capítulo, examinaremos conceptos clave como distribuciones de probabilidad, valor esperado, teorema de Bayes y estimación de máxima verosimilitud. Estos conceptos son esenciales para comprender el proceso de aprendizaje e inferencia en los modelos.

2.3.1 Distribuciones de probabilidad y valor esperado

Desafío: ¿Cómo se puede modelar matemáticamente la incertidumbre de datos reales?

Angustia del investigador: Los primeros investigadores en aprendizaje automático reconocieron que los datos del mundo real no podían ser explicados por reglas deterministas. Esto se debe a que los datos contienen errores de medición, ruido y variaciones impredecibles. Se necesitaban herramientas matemáticas para cuantificar esta incertidumbre e incorporarla en los modelos.

Una distribución de probabilidad representa todos los posibles resultados y sus probabilidades de ocurrencia. Estas pueden dividirse en distribuciones de probabilidad discretas y continuas.

Distribuciones de probabilidad discretas

Las distribuciones de probabilidad discretas tratan con variables aleatorias que pueden tomar un número finito o contable de valores. Su característica distintiva es que se puede asignar una probabilidad clara a cada resultado posible.

Matemáticamente, las distribuciones de probabilidad discretas se representan mediante la función de masa de probabilidad (PMF).

\[P(X = x) = p(x)\]

Aquí, ( p(x) ) es la probabilidad de que ( X ) tenga el valor ( x ). Las principales propiedades son las siguientes:

1. Para todo ( x ), ( 0 ≤ p(x) ≤ 1 )
2. ( _{x} p(x) = 1 )

Ejemplos típicos incluyen la distribución de Bernoulli, la distribución binomial y la distribución de Poisson.

La función de masa de probabilidad de tirar un dado es la siguiente:

\[P(X = x) = \begin{cases} \frac{1}{6} & \text{si } x \in \{1, 2, 3, 4, 5, 6\} \\ 0 & \text{en otro caso} \end{cases}\]

Las distribuciones de probabilidad discretas se utilizan en el aprendizaje automático y el aprendizaje profundo para problemas de clasificación, aprendizaje por refuerzo, procesamiento del lenguaje natural y otros campos. A continuación se presentan los resultados de una simulación de tirar un dado.

Resultado	Frecuencia
1	10
2	8
3	12
4	9
5	11
6	10

from dldna.chapter_02.statistics import simulate_dice_roll

simulate_dice_roll()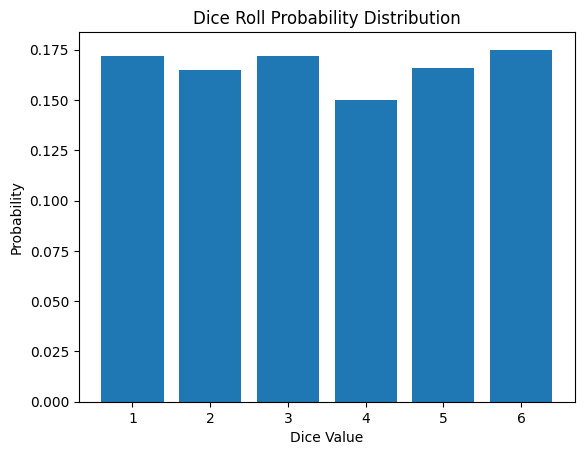

Distribución de probabilidad continua

La distribución de probabilidad continua trata los casos en los que una variable aleatoria puede tomar valores continuos. A diferencia de la distribución de probabilidad discreta, la probabilidad en un punto específico es 0 y se maneja la probabilidad para intervalos. Matemáticamente, la distribución de probabilidad continua se expresa mediante la función de densidad de probabilidad (Probability Density Function, PDF).

\[f(x) = \lim_{\Delta x \to 0} \frac{P(x < X \leq x + \Delta x)}{\Delta x}\]

Aquí, f(x) representa la densidad de probabilidad cerca de x. Las principales propiedades son las siguientes.

1. Para todo x, f(x) ≥ 0
2. \(\int_{-\infty}^{\infty} f(x) dx = 1\)

Ejemplos típicos incluyen la distribución normal, la distribución exponencial y la distribución gamma.

La función de densidad de probabilidad de la distribución normal es la siguiente.

\[f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

Aquí, μ es la media y σ es la desviación estándar.

La distribución de probabilidad continua se utiliza importante en diversos campos de aplicación del aprendizaje automático y el aprendizaje profundo, como problemas de regresión, procesamiento de señales y análisis de series temporales.

from dldna.chapter_02.statistics import plot_normal_distribution

plot_normal_distribution()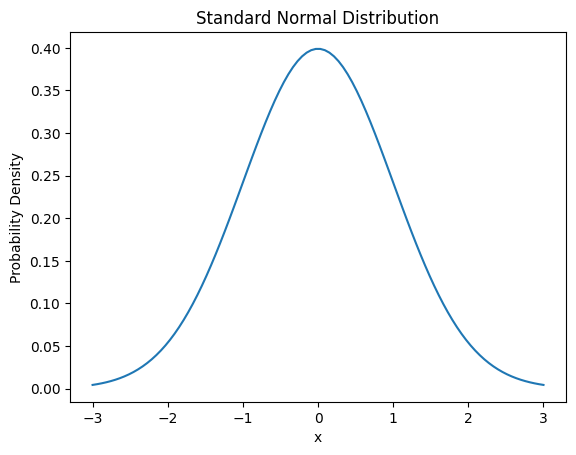

Valor esperado

El valor esperado es un concepto importante que indica la tendencia central de una distribución de probabilidad. Se puede interpretar como el promedio ponderado de todos los valores posibles de una variable aleatoria. En el caso de una distribución de probabilidad discreta, el valor esperado se calcula de la siguiente manera.

\[E[X] = \sum_{i} x_i P(X = x_i)\]

Donde \(x_i\) son los valores posibles de la variable aleatoria X y \(P(X = x_i)\) es la probabilidad de ese valor. Para una distribución de probabilidad continua, el valor esperado se calcula mediante integración.

\[E[X] = \int_{-\infty}^{\infty} x f(x) dx\]

Donde \(f(x)\) es la función de densidad de probabilidad. El valor esperado tiene las siguientes propiedades importantes:

1. Linealidad: \(E[aX + b] = aE[X] + b\)
2. Valor esperado del producto de variables aleatorias independientes: \(E[XY] = E[X]E[Y]\) (cuando X y Y son independientes)

En el aprendizaje profundo, el valor esperado se utiliza esencialmente para la minimización de funciones de pérdida o la estimación de parámetros del modelo. Por ejemplo, el error cuadrático medio (MSE) se define de la siguiente manera.

\[MSE = E[(Y - \hat{Y})^2]\]

Donde \(Y\) es el valor real y \(\hat{Y}\) es el valor predicho.

El concepto de valor esperado proporciona una base teórica para algoritmos de optimización como el descenso del gradiente estocástico (Stochastic Gradient Descent) y también se utiliza importantemente en la estimación de funciones de valor en el aprendizaje por refuerzo.

from dldna.chapter_02.statistics import calculate_dice_expected_value

calculate_dice_expected_value()

Expected value of dice roll: 3.5

Estos conceptos fundamentales de probabilidad y estadística juegan un papel crucial en el diseño, aprendizaje y evaluación de modelos de deep learning. En la siguiente sección, exploraremos el teorema de Bayes y la estimación de máxima verosimilitud basándonos en esto.

2.3.2 Teorema de Bayes y Estimación de Máxima Verosimilitud

Desafío: ¿Cómo estimar los parámetros del modelo lo mejor posible con datos limitados?

Angustia del investigador: Los estadísticos iniciales y los investigadores de aprendizaje automático a menudo se enfrentaban a la situación de tener que crear modelos con solo datos limitados. Estimar con precisión los parámetros del modelo en ausencia de suficientes datos era un problema muy difícil. Se necesitaba una forma de mejorar la precisión de las estimaciones utilizando no solo los datos, sino también conocimientos previos o creencias.

El teorema de Bayes y la estimación de máxima verosimilitud son conceptos fundamentales en probabilidad y estadística que se aplican ampliamente en el aprendizaje profundo para el entrenamiento e inferencia de modelos.

Teorema de Bayes

El teorema de Bayes proporciona un método para calcular probabilidades condicionales. Se utiliza para actualizar la probabilidad de una hipótesis dada nueva evidencia. La representación matemática del teorema de Bayes es como sigue:

\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]

Donde: - \(P(A|B)\) es la probabilidad de A dado B (probabilidad posterior) - \(P(B|A)\) es la probabilidad de B dado A (verosimilitud) - \(P(A)\) es la probabilidad de A (probabilidad a priori) - \(P(B)\) es la probabilidad de B (evidencia)

El teorema de Bayes se utiliza en el aprendizaje automático de las siguientes maneras:

1. Problemas de clasificación: Se usa para calcular la probabilidad de que una observación pertenezca a una clase específica en un clasificador Naive Bayes.
2. Estimación de parámetros: Se utiliza para calcular la distribución posterior de los parámetros del modelo.
3. Teoría de decisión: Se aplica para tomar decisiones óptimas bajo incertidumbre.

Estimación de Máxima Verosimilitud

La estimación de máxima verosimilitud (Maximum Likelihood Estimation, MLE) es un método para encontrar los parámetros del modelo que mejor explican los datos observados. En el contexto del aprendizaje profundo, esto implica encontrar los pesos y sesgos de una red neuronal que mejor expliquen los datos observados. Es decir, la estimación de máxima verosimilitud busca los parámetros que maximizan la probabilidad de que el modelo genere los datos de entrenamiento, lo cual está directamente relacionado con el proceso de entrenamiento del modelo. Matemáticamente, dado un conjunto de datos \(X = (x_1, ..., x_n)\), la función de verosimilitud para un parámetro \(\theta\) se define como:

\[L(\theta|X) = \prod_{i=1}^n P(x_i|\theta)\]

Para facilitar el cálculo, a menudo se utiliza el logaritmo de la función de verosimilitud:

\[\log L(\theta|X) = \sum_{i=1}^n \log P(x_i|\theta)\]

El uso del logaritmo de la verosimilitud tiene varias ventajas matemáticas importantes:

1. Conversión de multiplicación en suma: Debido a que \(\log(ab) = \log(a) + \log(b)\), el producto de probabilidades se convierte en una suma de logaritmos de probabilidades, lo que simplifica los cálculos y mejora la estabilidad numérica.
2. Mejor estabilidad numérica: Cuando se manejan valores de probabilidad muy pequeños, la multiplicación puede causar desbordamiento por debajo (underflow). El uso del logaritmo evita este problema.
3. Simplificación de derivadas: En el proceso de optimización, las derivadas son más fáciles de calcular cuando se utilizan funciones logarítmicas, especialmente en distribuciones exponenciales.
4. Función monótona creciente: Dado que la función logarítmica es monótona creciente, maximizar la verosimilitud y maximizar el logaritmo de la verosimilitud dan el mismo resultado.

Por estas razones, muchos algoritmos de aprendizaje automático, incluyendo los del aprendizaje profundo, utilizan el logaritmo de la verosimilitud para realizar optimización.

La estimación de máxima verosimilitud se utiliza en el aprendizaje profundo de las siguientes maneras: 1. Aprendizaje del modelo: el proceso de minimizar la función de pérdida al aprender los pesos de una red neuronal es, en esencia, equivalente a la estimación de máxima verosimilitud. 2. Modelado probabilístico: se utiliza para estimar la distribución de datos en modelos generativos. 3. Ajuste de hiperparámetros: puede ser utilizado para seleccionar los hiperparámetros del modelo.

El teorema de Bayes y la estimación de máxima verosimilitud están estrechamente relacionados. En la estimación bayesiana, cuando la distribución previa es uniforme, la estimación de máxima probabilidad a posteriori (MAP) se vuelve idéntica a la estimación de máxima verosimilitud. Matemáticamente, esto se expresa como \(P(\theta|X) \propto P(X|\theta)P(\theta)\) donde, si \(P(\theta)\) es constante, \(\operatorname{argmax}_{\theta} P(\theta|X) = \operatorname{argmax}_{\theta} P(X|\theta)P(\theta)\). Esto significa que cuando la distribución previa no proporciona información adicional sobre los parámetros, la estimación basada únicamente en los datos (MLE) coincide con la estimación bayesiana (MAP).

Estos conceptos son esenciales para comprender y optimizar el proceso de aprendizaje e inferencia en modelos de deep learning. En la siguiente sección, exploraremos los fundamentos de la teoría de la información.

Inmersión profunda: análisis detallado del teorema de Bayes

Teorema de Bayes - Análisis detallado

1. Derivación rigurosa del teorema de Bayes y espacio de probabilidad

• Espacio de probabilidad (Probability Space): El teorema de Bayes se define en el espacio de probabilidad \((\Omega, \mathcal{F}, P)\).
  • \(\Omega\): espacio muestral (Sample Space, conjunto de todos los resultados posibles)
  • \(\mathcal{F}\): espacio de eventos (Event Space, conjunto de subconjuntos del espacio muestral, \(\sigma\)-algebra)
  • \(P\): medida de probabilidad (Probability Measure, función que asigna una probabilidad a cada evento en el espacio de eventos)
• Definición rigurosa de la probabilidad condicional:
  • Para un evento \(B \in \mathcal{F}\) donde \(P(B) > 0\), la probabilidad condicional de un evento \(A \in \mathcal{F}\) dado \(B\) se define como: \(P(A|B) = \frac{P(A \cap B)}{P(B)}\)
• Probabilidad conjunta:
  • La probabilidad conjunta \(P(A \cap B)\) de dos eventos \(A, B \in \mathcal{F}\) representa la probabilidad de que ambos eventos ocurran simultáneamente.
  • Usando la definición de probabilidad condicional, se puede expresar como:
    • \(P(A \cap B) = P(A|B)P(B)\)
    • \(P(A \cap B) = P(B|A)P(A)\)
• Derivación del teorema de Bayes:
  1. \(P(A|B)P(B) = P(B|A)P(A)\) (dos expresiones de la probabilidad conjunta)
  2. \(P(A|B) = \frac{P(B|A)P(A)}{P(B)}\) (dividiendo ambos lados por \(P(B)\), \(P(B) > 0\))

2. Significado detallado y interpretación estadística de cada término del teorema de Bayes

• \(P(A|B)\): Probabilidad a posteriori (Posterior Probability)
  • Interpretación: Distribución de probabilidad actualizada para la hipótesis \(A\) después de obtener los datos observados \(B\). Representa el resultado de la inferencia basada en los datos.
  • Perspectiva bayesiana: La probabilidad a posteriori cuantifica la incertidumbre mediante la combinación de la probabilidad a priori y la verosimilitud, proporcionando una base para la toma de decisiones.
• \(P(B|A)\): Verosimilitud (Likelihood)
  • Interpretación: Probabilidad de observar los datos \(B\) dado que la hipótesis \(A\) es verdadera. Indica qué tan bien la hipótesis \(A\) explica los datos \(B\).
  • Perspectiva frecuentista vs. bayesiana:
    • Frecuentista: La verosimilitud es una función del parámetro (parameter) fijo que describe la distribución de los datos.
    • Bayesiana: La verosimilitud es una función que proporciona información sobre el parámetro dado los datos.
• \(P(A)\): Probabilidad a priori (Prior Probability)
  • Interpretación: Distribución de probabilidad que representa la creencia previa (prior belief) sobre la hipótesis \(A\) antes de obtener los datos observados \(B\).
  • Probabilidad a priori subjetiva vs. objetiva:
    • Subjetiva (Subjective): Establecida basada en el conocimiento experto, experiencias previas, etc.
    • Objetiva (Objective): Utiliza una distribución uniforme o un prior no informativo que contiene la mínima cantidad de información.
• \(P(B)\): evidencia (Evidence) o probabilidad marginal (Marginal Likelihood)
  • interpretación: probabilidad de que los datos observados \(B\) ocurran bajo todas las hipótesis posibles. Actúa como constante normalizadora (normalizing constant) para convertir \(P(A|B)\) en una distribución de probabilidad.
  • cálculo: \(P(B) = \sum_{A'} P(B|A')P(A')\) (para variables aleatorias discretas) \(P(B) = \int P(B|A)p(A) dA\) (para variables aleatorias continuas, donde \(p(A)\) es la función de densidad de probabilidad)
  • comparación de modelos: se usa para comparar la evidencia entre diferentes modelos, por ejemplo en el cálculo del factor de Bayes.

3. Teorema de Bayes y inferencia bayesiana (Bayesian Inference)

• punto clave: el teorema de Bayes es el principio fundamental de la inferencia bayesiana, que se utiliza para deducir la distribución de probabilidad de los parámetros o hipótesis dados los datos.
• proceso:
  1. Prior: se establece una distribución a priori \(p(\theta)\) para el parámetro \(\theta\).
  2. Likelihood: se define la probabilidad de observar los datos \(x\) dado el parámetro \(\theta\), \(p(x|\theta)\) (función de verosimilitud).
  3. Posterior: se calcula la distribución a posteriori \(p(\theta|x)\) utilizando el teorema de Bayes. \(p(\theta|x) = \frac{p(x|\theta)p(\theta)}{p(x)} = \frac{p(x|\theta)p(\theta)}{\int p(x|\theta')p(\theta') d\theta'}\)
  4. Inferencia: se realizan estimaciones, intervalos de confianza y pruebas de hipótesis sobre el parámetro basándose en la distribución a posteriori.
• actualización iterativa: es posible actualizar continuamente las creencias utilizando la distribución a posteriori previa como nueva distribución a priori cada vez que se recibe nuevo dato (actualización bayesiana secuencial).

4. Generalizaciones y aplicaciones del teorema de Bayes

• variables aleatorias continuas: aplicación del teorema de Bayes utilizando funciones de densidad de probabilidad.
• distribuciones a priori conjugadas (Conjugate Prior):
  • distribuciones a priori que aseguran que la distribución a posteriori pertenezca a la misma familia de distribuciones. Se usan por su comodidad en los cálculos (por ejemplo, distribución beta para datos bernoulli, distribución gamma para datos poisson).
• Bayes variacional (Variational Bayes):
  • método para aproximar distribuciones a posteriori complejas.
  • se busca una distribución manejable similar a la a posteriori y se minimiza la divergencia de Kullback-Leibler entre ambas distribuciones.
• MCMC (Markov Chain Monte Carlo):
  • método para estimar las características de la distribución a posteriori mediante el muestreo de esta.
  • incluye algoritmos como Metropolis-Hastings y Gibbs sampling.
• aplicaciones en deep learning:
  • Redes Neuronales Bayesianas: tratan los pesos de una red neuronal como variables aleatorias para cuantificar la incertidumbre en las predicciones.
  • Procesos Gaussianos: definen distribuciones a priori sobre espacios funcionales utilizando kernels y calculan distribuciones predictivas mediante el teorema de Bayes.

Inmersión profunda: análisis detallado de la estimación de máxima verosimilitud (MLE) y comparación con MAP (para estudiantes de posgrado)

Estimación de Máxima Verosimilitud (Maximum Likelihood Estimation, MLE) - Análisis profundo y comparación con MAP

1. Ejemplo concreto del cálculo de MLE

MLE es un método para encontrar el parámetro que mejor explica los datos observados. Se trata de encontrar el valor del parámetro que maximiza la verosimilitud de los datos observados.

• Función de Verosimilitud (Likelihood Function):

  • Si se asume que los datos \(x_1, x_2, ..., x_n\) son extraídos independientemente de una misma distribución de probabilidad (i.i.d), la función de verosimilitud se define como sigue. \[L(\theta; x_1, ..., x_n) = \prod_{i=1}^{n} p(x_i | \theta)\]
    • \(\theta\): parámetro (parameter)
    • \(p(x_i | \theta)\): probabilidad (o densidad de probabilidad) de que el dato \(x_i\) ocurra dado el parámetro \(\theta\)

• Función de Log-Verosimilitud (Log-Likelihood Function):

  • Para facilitar los cálculos, se utiliza la función de log-verosimilitud, que es el logaritmo de la función de verosimilitud. \[l(\theta; x_1, ..., x_n) = \log L(\theta; x_1, ..., x_n) = \sum_{i=1}^{n} \log p(x_i | \theta)\]
  • Ya que el logaritmo no cambia la posición del máximo valor, también se puede encontrar el parámetro que maximiza la log-verosimilitud.

• Procedimiento de cálculo de MLE:

  1. Definir la función de verosimilitud para los datos dados y el modelo de distribución de probabilidad.
  2. Aplicar el logaritmo a la función de verosimilitud para obtener la función de log-verosimilitud.
  3. Diferenciar la función de log-verosimilitud con respecto al parámetro \(\theta\).
  4. Encontrar el valor de \(\theta\) que hace que la derivada sea cero. (Si es necesario, usar la segunda derivada para determinar si es un máximo o mínimo)
  5. El valor de \(\theta\) encontrado es el estimador MLE.

• Ejemplo concreto:

  • Distribución Normal (Normal Distribution):
    • Supongamos que los datos \(x_1, ..., x_n\) siguen una distribución normal con media \(\mu\) y varianza \(\sigma^2\).
    • Función de log-verosimilitud: \[l(\mu, \sigma^2; x_1, ..., x_n) = -\frac{n}{2}\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^{n}(x_i - \mu)^2\]
    • Al diferenciar con respecto a \(\mu\) y \(\sigma^2\), y encontrar los puntos donde la derivada es cero, los estimadores MLE son:
      • \(\hat{\mu}_{MLE} = \frac{1}{n}\sum_{i=1}^{n} x_i\) (media de la muestra)
      • \(\hat{\sigma}^2_{MLE} = \frac{1}{n}\sum_{i=1}^{n} (x_i - \hat{\mu}_{MLE})^2\) (varianza de la muestra)
  • Distribución Bernoulli (Bernoulli Distribution):
    • Supongamos que los datos \(x_1, ..., x_n\) siguen una distribución de Bernoulli con probabilidad de éxito \(p\). (\(x_i = 1\) (éxito), \(x_i = 0\) (fracaso))
    • Función de log-verosimilitud: \[ l(p; x_1, ..., x_n) = \sum_{i=1}^n [x_i \log p + (1-x_i) \log (1-p)] \]
    • Al diferenciar con respecto a \(p\) y encontrar el punto donde la derivada es cero, el estimador MLE es:
      • \(\hat{p}_{MLE} = \frac{1}{n}\sum_{i=1}^{n} x_i\) (número de éxitos / número total de ensayos)

2. Ventajas y desventajas de MLE

• Ventajas:
  • Facilidad de cálculo: Es posible realizar estimaciones paramétricas con cálculos relativamente simples. (Especialmente en el caso de distribuciones de la familia exponencial)
  • Propiedades asintóticas (Asymptotic Properties): (Se explica más detalladamente a continuación)
    • Consistencia (Consistency): A medida que aumenta el tamaño de la muestra, la estimación MLE converge al parámetro real.
    • Normalidad asintótica (Asymptotic Normality): A medida que aumenta el tamaño de la muestra, la estimación MLE se aproxima a una distribución normal.
    • Eficiencia (Efficiency): Es un estimador insesgado con la varianza más pequeña asintóticamente (Cota inferior de Cramér–Rao).
• Desventajas:
  • Posibilidad de sobreajuste (Overfitting): En particular, cuando el tamaño de la muestra es pequeño, puede ajustarse excesivamente a los datos y disminuir el rendimiento general.
  • Sensibilidad a los valores atípicos (Outliers): Si existen valores atípicos, la estimación MLE puede distorsionarse significativamente.
  • No es aplicable a todas las distribuciones: MLE requiere un modelo probabilístico para ser aplicado (no se aplica a métodos no paramétricos).
  • Posibilidad de sesgo (Bias): En algunos casos, la estimación MLE puede estar sesgada (por ejemplo, en la estimación de la varianza de una distribución normal).

3. Comparación con la estimación de máxima probabilidad a posteriori (Maximum A Posteriori, MAP)

• MAP: Se basa en el teorema de Bayes y combina la probabilidad a priori y la verosimilitud para encontrar el parámetro que maximiza la probabilidad a posteriori.

• Estimación MAP: \[ \hat{\theta}_{MAP} = \arg\max_{\theta} p(\theta|x) = \arg\max_{\theta} \frac{p(x|\theta)p(\theta)}{p(x)} = \arg\max_{\theta} p(x|\theta)p(\theta) \]

  • \(p(\theta|x)\): Probabilidad a posteriori (Posterior Probability)
  • \(p(x|\theta)\): Verosimilitud (Likelihood)
  • \(p(\theta)\): Probabilidad a priori (Prior Probability)
  • \(p(x)\): Evidencia (Evidence, constante y por lo tanto se puede ignorar)

• MLE vs. MAP: | Característica | MLE | MAP | | ———————— | ——————————————————————– | ———————————————————————- | | Base | Frecuentista (Frequentist) | Bayesiana (Bayesian) | | Objetivo | Maximización de la verosimilitud | Maximización de la probabilidad a posteriori | | Probabilidad previa | No se considera | Se considera | | Resultado | Estimación puntual (Point Estimate) | Estimación puntual (generalmente) o estimación de distribución (en el caso de la inferencia bayesiana) | | Sobreajuste | Alta probabilidad de sobreajuste | Posible prevención del sobreajuste a través de la probabilidad previa (por ejemplo, efecto de regularización) | | Complejidad computacional | Generalmente baja | La complejidad puede aumentar según la probabilidad previa (especialmente si no es una distribución conjugada previa) |

• Influencia de la probabilidad previa:

  • Distribución previa no informativa (Non-informative Prior): Cuando la probabilidad previa sigue una distribución uniforme, como \(p(\theta) \propto 1\) (constante), la estimación MAP es idéntica a la estimación MLE.
  • Distribución previa informativa (Informative Prior): Cuando la probabilidad previa sigue una distribución específica (por ejemplo, normal o beta), la estimación MAP se ve influenciada por la probabilidad previa y difiere de la estimación MLE. Cuanto más fuerte es el prior belief representado por la distribución previa, más cercano será el posterior al prior.

4. Propiedad asintótica de MLE (Asymptotic Property)

• Consistencia (Consistency):
  • Cuando el tamaño de la muestra \(n\) tiende a infinito, el estimador MLE \(\hat{\theta}_{MLE}\) converge en probabilidad al parámetro real \(\theta_0\). \[\hat{\theta}_{MLE} \xrightarrow{p} \theta_0 \text{ as } n \rightarrow \infty\]
• Normalidad Asintótica (Asymptotic Normality):
  • Cuando el tamaño de la muestra \(n\) es suficientemente grande, la distribución del estimador MLE \(\hat{\theta}_{MLE}\) se aproxima a la siguiente distribución normal. \[\sqrt{n}(\hat{\theta}_{MLE} - \theta_0) \xrightarrow{d} N(0, I(\theta_0)^{-1})\]
    • \(I(\theta_0)\): Matriz de Información de Fisher (FIM)
      • \(I(\theta) = -E[\frac{\partial^2}{\partial \theta^2} l(\theta; x_1, ...,x_n)]\) (en el caso de un solo parámetro)
      • La FIM representa la curvatura de la función log-verosimilitud y significa la cantidad de información sobre el parámetro.
• Eficiencia (Efficiency):
  • El MLE es un estimador eficiente que asintóticamente alcanza el límite inferior de Cramér–Rao (CRLB). Tiene la varianza asintótica más pequeña en comparación con otros estimadores insesgados.

2.3.3 Fundamentos de la teoría de la información

Desafío: ¿Cómo medir la cantidad de información y cuantificar la incertidumbre?

Angustia del investigador: Claude Shannon se enfrentó a preguntas fundamentales sobre la transmisión eficiente y la compresión de la información en sistemas de comunicación. Necesitaba una base teórica para cuantificar la información, determinar hasta qué punto se podía comprimir los datos sin pérdida de información, y cómo transmitir la máxima cantidad de información de manera estable a través de canales ruidosos.

La teoría de la información es una teoría matemática que trata sobre la compresión, transmisión y almacenamiento de datos, y desempeña un papel crucial en la evaluación y optimización del rendimiento de los modelos en el aprendizaje profundo. En esta sección, exploraremos conceptos clave de la teoría de la información, como la entropía, la información mutua y la divergencia KL.

Entropía

La entropía es una medida de la incertidumbre de la información. La entropía H(P) de una distribución de probabilidad P se define como sigue:

\[H(P) = -\sum_{x} P(x) \log P(x)\]

Aquí, x representa todos los eventos posibles. Las principales características de la entropía son las siguientes.

1. No negatividad: \(H(P) ≥ 0\)
2. Máxima en distribuciones uniformes: La entropía es máxima cuando todas las probabilidades de los eventos son iguales.
3. Entropía cero para eventos seguros: Si \(P(x) = 1\), entonces \(H(P) = 0\)

En el aprendizaje profundo, la entropía se utiliza principalmente como base para la función de pérdida de entropía cruzada, que es común en problemas de clasificación. El siguiente ejemplo calcula la entropía para diferentes distribuciones de probabilidad y visualiza la entropía de una distribución binaria.

from dldna.chapter_02.information_theory import calculate_entropy
calculate_entropy()

Entropy of fair coin: 0.69
Entropy of biased coin: 0.33
Entropy of fair die: 1.39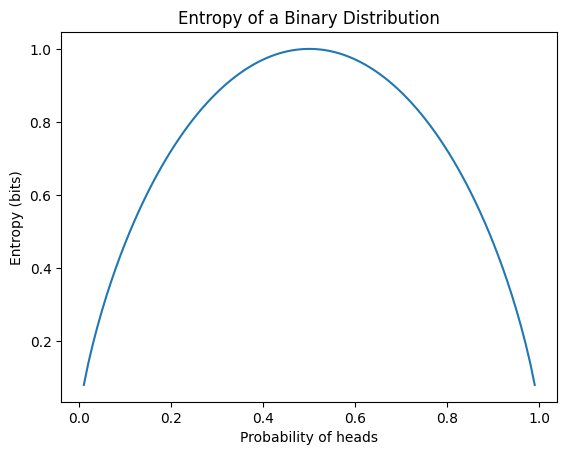

Información mutua

La información mutua (Mutual Information) mide la dependencia entre dos variables aleatorias X y Y. Matemáticamente, se define como sigue.

\[I(X;Y) = \sum_{x}\sum_{y} P(x,y) \log \frac{P(x,y)}{P(x)P(y)}\]

Las principales características de la información mutua son las siguientes:

1. No negatividad: \(I(X;Y) \ge 0\)
2. Simetría: \(I(X;Y) = I(Y;X)\)
3. Es cero cuando X y Y son independientes: Si X y Y son independientes, entonces \(I(X;Y) = 0\)

La información mutua se utiliza en diversas tareas de aprendizaje automático, como selección de características y reducción de dimensionalidad. El siguiente ejemplo calcula y visualiza la información mutua para una distribución de probabilidad conjunta simple.

from dldna.chapter_02.information_theory import mutual_information_example
mutual_information_example()

Mutual Information: 0.0058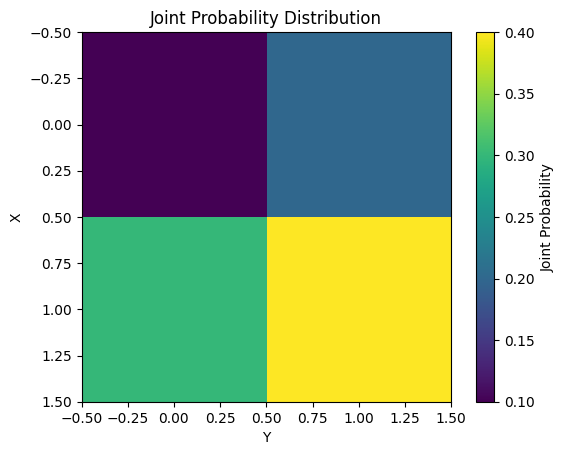

Divergencia KL

La divergencia KL (Kullback-Leibler) es un método para medir la diferencia entre dos distribuciones de probabilidad P y Q. La divergencia KL de Q con respecto a P se define como sigue.

\[D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\]

Las principales características de la divergencia KL son las siguientes:

1. No negatividad: \(D_{KL}(P||Q) \ge 0\)
2. Es cero solo si P = Q: \(D_{KL}(P||Q) = 0\) si y solo si \(P = Q\)
3. Asimetría: Generalmente \(D_{KL}(P||Q) \ne D_{KL}(Q||P)\)

La divergencia KL se utiliza en el aprendizaje profundo de las siguientes maneras:

1. Inferencia variacional: Se utiliza para minimizar la diferencia entre una distribución aproximada y una distribución real.
2. Compresión de modelos: Se utiliza en redes de maestro-alumno para la destilación de conocimiento.
3. Detección de anomalías: Se utiliza para medir la diferencia con respecto a la distribución de datos normales.

Los conceptos de la teoría de la información están estrechamente relacionados entre sí. Por ejemplo, la información mutua puede expresarse como la diferencia entre la entropía y la entropía condicional.

\(I(X;Y) = H(X) - H(X|Y)\)

Además, la divergencia KL se puede representar como la diferencia entre la entropía cruzada y la entropía.

\(D_{KL}(P||Q) = H(P,Q) - H(P)\)

Aquí, \(H(P,Q)\) es la entropía cruzada de \(P\) y \(Q\). A continuación se calcula la divergencia KL entre dos distribuciones de probabilidad y se visualizan las distribuciones.

from dldna.chapter_02.information_theory import kl_divergence_example
kl_divergence_example()

KL(P||Q): 0.0823
KL(Q||P): 0.0872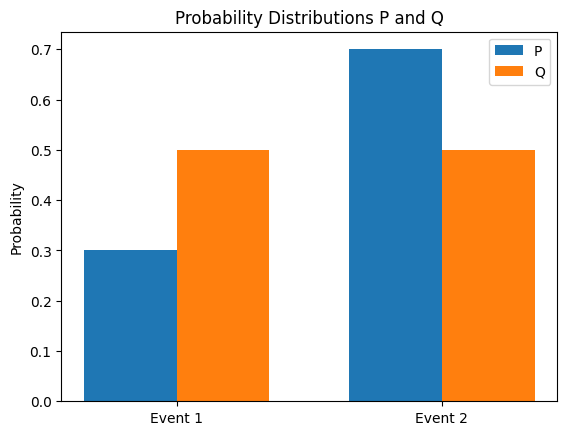

Estos conceptos de la teoría de la información se aplican ampliamente en el diseño y optimización de modelos de aprendizaje profundo. Por ejemplo, se utilizan de diversas maneras, como combinar el error de reconstrucción y la divergencia KL en la función de pérdida del autoencoder, o usar la divergencia KL como condición de restricción para la optimización de políticas en el aprendizaje por refuerzo.

En el siguiente capítulo examinaremos cómo estos conceptos de probabilidad, estadística y teoría de la información se aplican en modelos de aprendizaje profundo reales.

Inmersión profunda: conceptos clave de la teoría de la información

Teoría de la Información Conceptos Clave - Information Content, Cross Entropy, KL-Divergence, Mutual Information

1. Information Content (Self-information)

• Definición: La cantidad de información (Information Content, Self-information) representa la cantidad de información que se obtiene cuando ocurre un evento específico. Cuanto más raro es el evento, mayor será su contenido informativo.

• Fórmula: \[I(x) = -\log(P(x))\]

  • \(x\): evento
  • \(P(x)\): probabilidad de que ocurra el evento \(x\)
  • \(\log\): la base del logaritmo puede ser 2 (unidad: bits), \(e\) (unidad: nats), o 10, entre otras. En aprendizaje profundo, se suele usar el logaritmo natural (\(e\)).

• Explicación Intuitiva:

  • Rarez: Cuanto menor sea la probabilidad de un evento (raro), mayor será su cantidad de información. Por ejemplo, “el sol sale por el este” es un hecho obvio y tiene poco contenido informativo, mientras que “gané el premio mayor de la lotería hoy” es un evento muy raro y tiene mucho contenido informativo.
  • Reducción de Incertidumbre: La cantidad de información puede interpretarse como una medida de cuánto se reduce la incertidumbre antes del evento después de que este ocurre.

• Propiedades:

  • \(0 \le P(x) \le 1\) por lo tanto, \(I(x) \ge 0\).
  • Si \(P(x) = 1\) (evento seguro), entonces \(I(x) = 0\).
  • Cuanto menor sea \(P(x)\), mayor será \(I(x)\).
  • Para dos eventos independientes \(x\) y \(y\), \(I(x, y) = I(x) + I(y)\) (aditividad de la cantidad de información).

2. Cross Entropy

• Definición: La entropía cruzada (Cross Entropy) es una medida que indica cuán diferentes son dos distribuciones de probabilidad \(P\) y \(Q\). Si \(P\) es la distribución verdadera y \(Q\) es la distribución estimada, la entropía cruzada representa el número promedio de bits necesarios para representar \(P\) utilizando \(Q\).

• Derivación:

  1. Cantidad de Información: La cantidad de información del evento \(x\) que sigue la distribución verdadera \(P\): \(I(x) = -\log P(x)\)
  2. Cantidad de Información Promedio (Entropía): La cantidad de información promedio (entropía) para la distribución verdadera \(P\): \(H(P) = -\sum_{x} P(x) \log P(x)\)
  3. Uso de Distribución Estimada: Al usar la distribución estimada \(Q\) para representar la distribución verdadera \(P\), la cantidad de información para cada evento \(x\): \(-\log Q(x)\)
  4. Entropía Cruzada: La cantidad de información promedio al usar la distribución estimada \(Q\) para representar la distribución verdadera \(P\): \[H(P, Q) = -\sum_{x} P(x) \log Q(x)\]

• Explicación Intuitiva:

  • Cuanto más similares sean \(P\) y \(Q\), menor será la entropía cruzada.
  • Si \(P = Q\), la entropía cruzada alcanza su valor mínimo (entropía \(H(P)\)).
  • Cuanto más diferentes sean \(P\) y \(Q\), mayor será la entropía cruzada. Es decir, si la distribución estimada no refleja bien la distribución real, se produce una pérdida de información.

• Binary Cross Entropy (BCE):

  • Se utiliza en problemas de clasificación binaria con dos clases (0 o 1).
  • \(P = [p, 1-p]\) (distribución de probabilidad de la clase real, donde \(p\) es la probabilidad de la clase 1)
  • \(Q = [q, 1-q]\) (distribución de probabilidad de la clase predicha, donde \(q\) es la probabilidad de predecir la clase 1)
  • \[H(P, Q) = -[p \log q + (1-p) \log (1-q)]\]

• Categorical Cross Entropy (CCE):

  • Se utiliza en problemas de clasificación multiclase con múltiples clases.
  • \(P = [p_1, p_2, ..., p_k]\) (distribución de probabilidad real de la clase, \(p_i\) es la probabilidad de la clase \(i\), one-hot encoding)
  • \(Q = [q_1, q_2, ..., q_k]\) (distribución de probabilidad predicha de la clase, \(q_i\) es la probabilidad de predecir la clase \(i\), softmax)
  • \[H(P, Q) = -\sum_{i=1}^{k} p_i \log q_i\]

3. Cross Entropy y Likelihood

• Likelihood (verosimilitud): La probabilidad de que los datos dados ocurran en un modelo específico (parámetros).
• Negative Log-Likelihood (NLL): El valor logarítmico negativo de la verosimilitud.
• Relación entre Cross Entropy y NLL:
  • En problemas de clasificación, cuando se considera la salida del modelo (distribución de probabilidad predicha) como \(Q\) y las etiquetas reales (one-hot encoding) como \(P\), la Cross Entropy es igual a la Negative Log-Likelihood.
  • Minimizar la Cross Entropy es equivalente a maximizar la Likelihood (Estimación del Máximo de Verosimilitud, MLE).
• Uso en Deep Learning:
  • En deep learning, utilizar la Cross Entropy como función de pérdida para problemas de clasificación equivale a entrenar el modelo para que su salida siga la distribución de las etiquetas reales (desde una perspectiva MLE).

4. Relación entre KL-Divergence y Cross Entropy

• KL-Divergence (Divergencia Kullback-Leibler):

  • Otra manera de medir la diferencia entre dos distribuciones de probabilidad \(P\) y \(Q\) (no es una distancia, es asimétrica).
  • La KL-Divergence de \(P\) a \(Q\) representa la cantidad adicional de información necesaria para representar \(P\) usando \(Q\).
  • \[D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)} = \sum_{x} P(x)[\log P(x) - \log Q(x)]\]

• Relación entre KL-Divergence y Cross Entropy:

  \[D_{KL}(P||Q) = \sum_{x} P(x) \log P(x) - \sum_{x} P(x) \log Q(x) = -\sum_{x} P(x) \log Q(x) - (-\sum_{x} P(x) \log P(x))\] \[D_{KL}(P||Q) = H(P, Q) - H(P)\]

  • \(H(P,Q)\): Cross Entropy

  • \(H(P)\): Entropy

  • La KL-Divergence es la diferencia entre la Cross Entropy y la Entropy de \(P\).

  • Cuando \(P\) está fija, minimizar la Cross Entropy es equivalente a minimizar la KL-Divergence.

5. Relación entre Mutual Information y Conditional Entropy

• Mutual Information (Información Mutua):

  • Una medida que indica cuánta información comparten dos variables aleatorias \(X\) y \(Y\).
  • Indica cuánto se reduce la incertidumbre de \(Y\) al conocer \(X\) (o viceversa).
  • \[I(X;Y) = \sum_{x, y} P(x, y) \log \frac{P(x, y)}{P(x)P(y)}\]
    • \(P(x,y)\): distribución de probabilidad conjunta (Joint Probability Distribution)
    • \(P(x)\), \(P(y)\): distribuciones de probabilidad marginales (Marginal Probability Distribution)

• Entropía Condicional (entropía condicional):

  • Representa la incertidumbre de la variable aleatoria \(X\) dado que se conoce la variable aleatoria \(Y\). \[H(X|Y) = -\sum_{y} P(y) \sum_{x} P(x|y) \log P(x|y) = -\sum_{x,y} P(x,y) \log P(x|y)\]

• Relación entre Información Mutua y Entropía Condicional: \[I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)\]

  • La cantidad de información mutua entre \(X\) y \(Y\) es igual a la entropía de \(X\) menos la entropía condicional de \(X\) dado \(Y\).
  • Muestra cuánto disminuye la incertidumbre sobre \(X\) al conocer \(Y\).

6. Divergencia Jensen–Shannon

• Divergencia Jensen–Shannon (JSD):
  • Otra forma de medir la distancia entre dos distribuciones de probabilidad \(P\) y \(Q\). A diferencia de la divergencia KL, es simétrica (symmetric) y acotada (entre 0 y 1).
  • \[JSD(P||Q) = \frac{1}{2}D_{KL}(P||M) + \frac{1}{2}D_{KL}(Q||M)\]
    • \(M = \frac{1}{2}(P + Q)\): distribución media de \(P\) y \(Q\)
• Características:
  • Simetría: \(JSD(P||Q) = JSD(Q||P)\)
  • Acotación: \(0 \le JSD(P||Q) \le 1\) (cuando se usa logaritmo base 2)
  • La raíz cuadrada de JSD satisface las condiciones de una función métrica.

2.3.4 Función de pérdida

La función de pérdida (Loss Function) es una función que mide cuánto difiere la predicción del modelo de aprendizaje automático de los valores reales. El objetivo del entrenamiento del modelo es encontrar los parámetros (pesos y sesgos) que minimicen el valor de esta función de pérdida. La elección de una función de pérdida adecuada tiene un gran impacto en el rendimiento del modelo, por lo tanto, debe seleccionarse cuidadosamente según el tipo de problema y las características de los datos.

Definición de la función de pérdida

En general, la función de pérdida \(L\) se puede expresar como sigue cuando \(\theta\) son los parámetros del modelo y \((x_i, y_i)\) es un punto de datos. (Aquí, \(y_i\) es el valor real y \(f(x_i; \theta)\) es el valor predicho por el modelo)

\(L(\theta) = \frac{1}{N} \sum_{i=1}^{N} l(y_i, f(x_i; \theta))\)

\(N\) es el número de puntos de datos, y \(l\) es la función que representa la pérdida para un punto de datos individual (loss term).

Funciones de pérdida principales

A continuación se presentan las funciones de pérdida más comúnmente utilizadas en aprendizaje automático y aprendizaje profundo.

1. Error cuadrático medio (Mean Squared Error, MSE)

• Fórmula: \(MSE = \frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2\) (\(y_i\): valor real, \(\hat{y}_i\): valor predicho)
• Características:
  • Dado que se eleva al cuadrado el error, es sensible a los valores atípicos (outliers).
  • Es diferenciable y una función convexa, lo que facilita encontrar la solución óptima mediante métodos de descenso de gradiente.
• Uso: Se utiliza principalmente en problemas de regresión.

2. Error absoluto medio (Mean Absolute Error, MAE)

• Fórmula: \(MAE = \frac{1}{N} \sum_{i=1}^N |y_i - \hat{y}_i|\)
• Características:
  • Es menos sensible a los valores atípicos que el MSE.
  • No es diferenciable en x=0, pero puede ser manejado por frameworks de aprendizaje profundo mediante diferenciación automática.
• Uso: Se utiliza en problemas de regresión.

3. Pérdida de entropía cruzada (Cross-Entropy Loss)

• Fórmula:
  • Clasificación binaria (Binary Classification): \(L = -\frac{1}{N} \sum_{i=1}^N [y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)]\)
  • Clasificación multiclase (Multi-class Classification): \(L = -\frac{1}{N} \sum_{i=1}^N \sum_{c=1}^{C} y_{ic} \log(\hat{y}_{ic})\) (\(C\): número de clases)
• Características:
  • Tiende a converger más rápidamente en problemas de clasificación.
  • Se utiliza junto con la función de activación softmax en la capa de salida.
• Uso: Problemas de clasificación (clasificación binaria, clasificación multiclase)

4. Pérdida del borde (Hinge Loss)

• Fórmula: \(L = \max(0, 1 - y \cdot f(x))\) (\(y\): {-1, 1} clase real, \(f(x)\): valor predicho por el modelo)
• Características:
  • Maximiza el margen (margin) entre “correcto” y “incorrecto”.
  • No es diferenciable en x=1.
• Uso: Se utiliza principalmente en problemas de clasificación binaria, como en las máquinas de vectores de soporte (SVM).

Criterios para elegir la función de pérdida

• Tipo de problema: La elección de la función de pérdida adecuada depende de si el problema es de regresión o clasificación.
• Características de los datos: Factores como la presencia de valores atípicos y el desequilibrio de clases pueden influir en la selección de la función de pérdida apropiada.
• Modelo: La elección de la función de pérdida también puede depender del modelo que se esté utilizando.

Funciones de pérdida adicionales

• Divergencia Kullback-Leibler (KLD): mide la diferencia entre dos distribuciones de probabilidad P y Q. Se utiliza principalmente en modelos generativos como el Variational Autoencoder (VAE).
• Focal Loss: una función de pérdida que ajusta la Cross-Entropy para funcionar bien con datos desequilibrados. Se utiliza principalmente en problemas de detección de objetos.
• Huber Loss: combina las características del MSE y el MAE, es robusto a los valores atípicos y diferenciable.
• Log-Cosh Loss: similar al Huber Loss, pero con la ventaja de ser dos veces diferenciable en todos los puntos.
• Contrastive Loss: utilizado en redes Siamesas, aprende incrustaciones que colocan pares de muestras similares cerca y pares de muestras no similares lejos entre sí.
• Triplet Loss: utiliza tres muestras: Anchor, Positive y Negative, para aprender incrustaciones que minimicen la distancia entre el Anchor y la muestra Positive mientras maximiza la distancia entre el Anchor y la muestra Negative.
• CTC Loss: una función de pérdida utilizada en reconocimiento de voz, reconocimiento de escritura, etc., cuando las longitudes de las secuencias de entrada y salida difieren.

Haga clic para ver el contenido (deep dive: análisis detallado de la función de pérdida)

Análisis profundo de la función de pérdida

Función de pérdida y estimación de máxima verosimilitud (Maximum Likelihood Estimation, MLE)

Muchos modelos de aprendizaje automático pueden explicarse desde la perspectiva de la estimación de máxima verosimilitud (MLE). El MLE es un método para encontrar los parámetros del modelo que mejor explican los datos observados. Si se asume que los datos son independientes e idénticamente distribuidos (i.i.d.), la función de verosimilitud se define como sigue.

\(L(\theta) = P(D|\theta) = \prod_{i=1}^{N} P(y_i | x_i; \theta)\)

Aquí, \(D = \{(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)\}\) es el conjunto de datos de entrenamiento, \(\theta\) son los parámetros del modelo. \(P(y_i | x_i; \theta)\) es la probabilidad (o densidad de probabilidad) de que el modelo genere \(y_i\) dado \(x_i\).

El objetivo del MLE es encontrar los parámetros \(\theta\) que maximizan la función de verosimilitud \(L(\theta)\). En la práctica, es más conveniente computacionalmente maximizar la función de log-verosimilitud (log-likelihood function).

\(\log L(\theta) = \sum_{i=1}^{N} \log P(y_i | x_i; \theta)\)

• MSE y MLE: En el caso de un modelo de regresión lineal, si se asume que los errores siguen una distribución normal con media 0 y varianza \(\sigma^2\), entonces la MLE es equivalente a minimizar el MSE.

  \(P(y_i | x_i; \theta) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - f(x_i; \theta))^2}{2\sigma^2}\right)\)

  La función de log-verosimilitud es la siguiente. \(\log L(\theta) = -\frac{N}{2}\log(2\pi\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^{N}(y_i - f(x_i;\theta))^2\)

  Excluyendo las constantes, y asumiendo que \(\sigma^2\) es constante, maximizar la función de log-verosimilitud es equivalente a minimizar el MSE.

• Cross-Entropy y MLE: En problemas de clasificación, los valores de salida \(\hat{y}_i\) pueden interpretarse como parámetros de una distribución de Bernoulli (clasificación binaria) o multinomial (clasificación multiclase). En este caso, la MLE es equivalente a minimizar la Loss de Cross-Entropy.

  • Clasificación binaria (distribución de Bernoulli): Si \(\hat{y_i}\) representa la probabilidad que el modelo predice para \(y_i=1\), \(P(y_i|x_i;\theta) = \hat{y_i}^{y_i} (1 - \hat{y_i})^{(1-y_i)}\) Log-verosimilitud: \(\log L(\theta) = \sum_{i=1}^{N} [y_i \log(\hat{y}_i) + (1 - y_i)\log(1 - \hat{y}_i)]\)

  • Clasificación multiclase (Distribución Categórica/Multinomial): \(P(y_i | x_i; \theta) = \prod_{j=1}^{C} \hat{y}_{ij}^{y_{ij}}\) (codificación one-hot) Log-verosimilitud: \(\log L(\theta) = \sum_{i=1}^N \sum_{j=1}^C y_{ij} \log(\hat{y}_{ij})\)

  Por lo tanto, minimizar la Loss de Cross-Entropy es un proceso equivalente a encontrar los parámetros que mejor modelan la distribución de los datos según MLE.

Funciones de pérdida adicionales (KLD, Focal Loss)

• Divergencia Kullback-Leibler (KLD):

• Descripción: Mide la diferencia entre dos distribuciones de probabilidad P y Q. P representa la distribución de los datos reales, y Q representa la distribución estimada por el modelo.

  • Fórmula: \(D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\)
  • Características:
    • Asimétrica (asymmetric): \(D_{KL}(P||Q) \neq D_{KL}(Q||P)\)
    • Siempre mayor o igual a 0: \(D_{KL}(P||Q) \ge 0\), solo cuando \(P=Q\) se tiene que \(D_{KL}(P||Q) = 0\)
    • Problemas de definición donde P(x) = 0
  • Relación con VAEs:
    • En los autoencoders variacionales (Variational Autoencoder, VAE), la divergencia KL se utiliza para hacer que la distribución a posteriori de las variables latentes sea similar a una distribución previa, como la normal.
    • La función de pérdida del VAE consta de una pérdida de reconstrucción y un término de divergencia KL.

• Focal Loss:

  • Descripción: Se propuso para abordar problemas de desequilibrio de clases, especialmente entre ejemplos “fáciles” (easy examples) y ejemplos “difíciles” (hard examples), modificando la Cross-Entropy Loss.
  • Fórmula: \(FL(p_t) = -\alpha_t (1 - p_t)^\gamma \log(p_t)\)
    • \(p_t\): probabilidad predicha por el modelo para la clase correcta
    • \(\gamma\): parámetro de enfoque (\(\gamma \ge 0\), generalmente 2)
    • \(\alpha_t\): pesos por clase (opcional)
  • Características:
    • Si \(\gamma = 0\), es igual a la Cross-Entropy Loss normal.
    • Si \(\gamma > 0\), disminuye la pérdida de los ejemplos bien clasificados (\(p_t\) alto) y mantiene alta la pérdida de los mal clasificados (\(p_t\) bajo). Es decir, se centra más en los ejemplos difíciles durante el aprendizaje.
    • Se pueden ajustar los pesos por clase usando \(\alpha_t\) (por ejemplo, dando un peso mayor a las clases con menos muestras).
  • Aplicación en detección de objetos:
    • En problemas de detección de objetos, las áreas de fondo (negative) son mucho más numerosas que las áreas de objeto (positive), lo que provoca un desequilibrio de clases grave.
    • El Focal Loss ayuda a mitigar este desequilibrio, haciendo que el modelo de detección de objetos se centre más en los objetos reales y no tanto en el fondo durante el aprendizaje.

Diferentes funciones de pérdida (avanzado)

• Huber Loss: Es una función de pérdida que combina las ventajas del MSE y el MAE. Usa el error cuadrático cuando el error es menor a un valor específico (\(\delta\)), y el error absoluto cuando el error es grande, lo que la hace robusta frente a valores atípicos y diferenciable.

  \(L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 & \text{si } |y - \hat{y}| \le \delta \\ \delta(|y - \hat{y}| - \frac{1}{2}\delta) & \text{en otro caso} \end{cases}\)

• Log-Cosh Loss: Se define como \(\log(\cosh(y - \hat{y}))\). Similar al Huber Loss, es robusta frente a valores atípicos y tiene la ventaja de ser dos veces diferenciable en todos los puntos.

• Quantile Loss: Se utiliza para minimizar el error de predicción en un cuantil específico.

• Contrastive Loss, Triplet Loss: Se utilizan en redes Siamesas, redes Triplet, y se usan para ajustar la distancia entre pares/tripletas de muestras similares. (Consulte los documentos relevantes para más detalles)

• Connectionist Temporal Classification (CTC) Loss: Se utiliza cuando la alineación (alignment) entre secuencias de entrada y salida no es clara, como en el reconocimiento de voz y escritura.

Guía para la selección de funciones de pérdida (avanzado)

• Manejo de valores atípicos: Si hay muchos valores atípicos y se requiere robustez frente a ellos, puede considerar MAE, Huber Loss, Quantile Loss.
• Diferenciabilidad: Para la optimización basada en el descenso del gradiente, es necesario una función de pérdida diferenciable. Sin embargo, incluso con funciones no diferenciables como Hinge Loss y MAE, se pueden usar subgradientes (subdiferenciales) o la diferenciación automática de marcos de deep learning para resolverlo.
• Modelado probabilístico: Si desea interpretar las salidas del modelo como una distribución de probabilidad, Cross-Entropy Loss es adecuado.
• Desbalanceo de clases: En caso de un desbalanceo de clases severo, puede considerar Focal Loss, Weighted Cross-Entropy.
• Salidas múltiples: Si hay varias salidas y existe una correlación entre ellas, puede combinar las funciones de pérdida para cada salida.

Las funciones de pérdida son un elemento crucial que determina el rendimiento de los modelos de deep learning. Se requiere la capacidad de seleccionar una función de pérdida adecuada considerando las características del problema, la distribución de los datos y la estructura del modelo, e incluso diseñar nuevas funciones de pérdida si es necesario.

Haga clic para ver el contenido (deep dive: diseño de nuevas funciones de pérdida)

Diseño de nuevas funciones de pérdida

Las funciones de pérdida existentes (MSE, Entropía Cruzada, etc.) no siempre son la mejor opción. Dependiendo de las exigencias específicas del problema, la distribución de los datos y la estructura del modelo, puede ser necesario diseñar nuevas funciones de pérdida. El diseño de nuevas funciones de pérdida es una parte importante de la investigación en deep learning y tiene el potencial de mejorar significativamente el rendimiento del modelo.

Casos en los que se necesitan nuevas funciones de pérdida

• Estructura especial de los datos: Cuando los datos no siguen distribuciones comunes (Gaussiana, Bernoulli, etc.) o tienen una estructura especial (por ejemplo: orden, rareza, estructura jerárquica, estructura de grafo).
• Restricciones especiales del problema: Cuando se desea imponer restricciones específicas a las predicciones del modelo (por ejemplo: monotonicidad, rareza, equidad, robustez).
• Limitaciones de las funciones de pérdida existentes: Cuando las funciones de pérdida existentes no funcionan bien en un problema específico (por ejemplo: sensibilidad a los valores atípicos, desequilibrio de clases) o no reflejan adecuadamente el objetivo deseado. Cuando se desea optimizar directamente una métrica específica.
• Optimización multiobjetivo: Cuando es necesario combinar varias funciones de pérdida para optimizarlas simultáneamente (por ejemplo: equilibrar precisión predictiva y complejidad del modelo).
• Modelos generativos: Los modelos generativos tienen como objetivo aprender la distribución de los datos, por lo que requieren funciones de pérdida diferentes a las usadas en problemas de clasificación/regresión comunes.

Principios para el diseño de nuevas funciones de pérdida

Al diseñar nuevas funciones de pérdida, se deben considerar los siguientes principios:

1. Definición del problema y objetivos: Se debe definir claramente el problema que se desea resolver y el objetivo final del modelo. La función de pérdida es un elemento clave que define lo que el modelo debe aprender (por ejemplo: si solo se trata de aumentar la precisión de clasificación, mejorar las predicciones para una clase específica, ajustar la ratio de False Positive/False Negative, etc.).

2. Validez matemática:

   • Diferenciabilidad (Differentiability): Para la optimización basada en el descenso del gradiente, la función de pérdida debe ser diferenciable (casi) en todos los puntos. Si existen puntos no diferenciables, se deben poder usar subgradientes (subdiferenciales).
   • Convexidad (Convexity): Si la función de pérdida es convexa, se puede garantizar que se encuentra el mínimo global. En el caso de funciones no convexas, se debe diseñar para encontrar buenos mínimos locales.
   • Prevención del desvanecimiento/explotación del gradiente: Gradientes demasiado grandes o pequeños pueden hacer que el aprendizaje sea inestable. Se debe tener cuidado de que en situaciones específicas, como el problema “dying ReLU” o el desvanecimiento del gradiente con sigmoid/tanh, el gradiente no se haga 0 o muy pequeño.
   • Invariancia a la escala: El valor de la función de pérdida no debe cambiar significativamente según la escala de los datos de entrada o de los parámetros.

3. Interpretabilidad: Si la función de pérdida tiene un significado intuitivo, puede ser útil para analizar y depurar el proceso de aprendizaje del modelo. Cada término (term) debe tener un rol y un significado claros. El significado e impacto de los hiperparámetros también deben ser claros.

4. Eficiencia computacional: La función de pérdida se calcula en cada iteración y para todos (o mini-lotes) los puntos de datos, por lo que si el costo de cálculo es muy alto, la velocidad de aprendizaje puede disminuir significativamente.

Metodología para el diseño de nuevas funciones de pérdida

1. Modificación/Combinación de funciones de pérdida existentes:

   • Adición de pesos: se asignan mayores pesos a ciertos puntos de datos, clases o salidas (por ejemplo: Weighted Cross-Entropy, Focal Loss).
   • Adición de términos de regularización: se agregan términos de regularización para limitar la complejidad del modelo o fomentar ciertas propiedades (por ejemplo: L1 regularization, L2 regularization, Elastic Net). También se pueden agregar términos de regularización para suavizar las salidas.
   • Combinación de múltiples funciones de pérdida: se combinan linealmente varias funciones de pérdida existentes o se combinan de otras maneras (por ejemplo: Multi-task learning).
   • Label Smoothing Soft/Hard: la Regularización por Suavizado de Etiquetas evita que el modelo sea demasiado confiado en las respuestas correctas.

2. Diseño basado en modelado probabilístico:

   • Estimación de Máxima Verosimilitud (MLE): se diseña la función de pérdida desde la perspectiva de estimar los parámetros de una distribución asumida para los datos (por ejemplo: MSE es MLE bajo la suposición de una distribución gaussiana, Cross-Entropy es MLE bajo la suposición de una distribución Bernoulli/multinomial).
   • Inferencia Variacional: se diseña la función de pérdida (ELBO, Evidence Lower Bound) para aproximar una distribución posterior intractable usando métodos de inferencia aproximada (por ejemplo: Variational Autoencoder).
   • Verosimilitud Implícita: en modelos generativos donde es difícil calcular la verosimilitud explícitamente, se utilizan métodos sin verosimilitud (por ejemplo: GAN).

3. Diseño de funciones de pérdida especializadas para problemas específicos:

   • Función de Pérdida de Ranking: se diseña una función de pérdida adecuada para problemas de clasificación por ranking (por ejemplo: pairwise ranking loss, listwise ranking loss, margin ranking loss).
   • Función de Pérdida de Detección de Objetos: en problemas de detección de objetos, se diseña una función de pérdida que considere la regresión del bounding box y la clasificación de clases simultáneamente (por ejemplo: las funciones de pérdida de YOLO, SSD, Faster R-CNN).
   • Función de Pérdida de Segmentación: en problemas de segmentación de imágenes, se diseña una función de pérdida que prediga la clase de cada píxel y minimice la diferencia con el mapa de segmentación ground truth (por ejemplo: Dice Loss, IoU Loss, Tversky Loss).
   • Función de Pérdida de Modelos Generativos: funciones de pérdida para generadores y discriminadores en modelos generativos como GAN, VAE (por ejemplo: Wasserstein distance, Adversarial Loss).
   • Función de Pérdida de Aprendizaje Métrico: Contrastive Loss, Triplet Loss, N-pair Loss, etc.
   • Función de Pérdida de Secuencia: CTC Loss, Cross-Entropy en modelos sequence-to-sequence, etc.
   • Función de Pérdida de Datos de Grafo: funciones de pérdida utilizadas en Graph Neural Networks (clasificación de nodos, predicción de enlaces, clasificación de grafos, etc.)

Precauciones al diseñar nuevas funciones de pérdida

• Complejidad excesiva: una función de pérdida demasiado compleja puede dificultar el aprendizaje y causar sobreajuste (overfitting). Es mejor comenzar con funciones de pérdida simples e incrementar gradualmente la complejidad.
• Ajuste de hiperparámetros: una nueva función de pérdida a menudo incluye hiperparámetros adicionales (por ejemplo, \(\gamma\) en Focal Loss, pesos en combinaciones ponderadas). Es importante ajustar estos hiperparámetros adecuadamente y encontrar sus valores óptimos mediante técnicas como la validación cruzada (cross-validation).
• Fundamento teórico/empírico: al proponer una nueva función de pérdida, es necesario presentar un fundamento teórico (por ejemplo, características matemáticas específicas del problema, relación con el MLE) o empírico (por ejemplo, resultados experimentales) que explique por qué la función de pérdida funciona bien.

Diseñar una nueva función de pérdida es un proceso creativo, pero también requiere un enfoque cuidadoso. Es importante comprender profundamente la naturaleza del problema, diseñar sobre principios matemáticos/estadísticos y validar el rendimiento a través de experimentos rigurosos.

En este capítulo hemos examinado las bases matemáticas del aprendizaje profundo. Hemos visto cómo los conceptos de diferentes campos, como el álgebra lineal, el cálculo, la probabilidad y estadística, y la teoría de la información, se utilizan en el diseño, el aprendizaje y el análisis de los modelos de aprendizaje profundo. Estas herramientas matemáticas son esenciales para comprender las complejas estructuras de redes neuronales, desarrollar algoritmos de aprendizaje eficientes, evaluar y mejorar el rendimiento del modelo. También desempeñan un papel importante en encontrar nuevas vías de avance en la investigación de aprendizaje profundo.

Ejercicios de práctica

1. Álgebra lineal

Básico

1. Calcule el producto escalar (dot product) de los vectores \(\mathbf{a} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\) y \(\mathbf{b} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\).

2. Calcule el producto \(\mathbf{Ab}\) de la matriz \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) y el vector \(\mathbf{b} = \begin{bmatrix} 5 \\ 6 \end{bmatrix}\).

3. Genere una matriz identidad (identity matrix) de tamaño 2x2.

4. Escriba las definiciones de la norma L1 y la norma L2 de un vector, y calcule la norma L1 y la norma L2 del vector \(\mathbf{v} = \begin{bmatrix} 3 \\ -4 \end{bmatrix}\).

Aplicado

1. Encuentre los valores propios (eigenvalues) y vectores propios (eigenvectors) de la matriz \(\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\).

2. Determine si existe la matriz inversa de la matriz dada, y si es así, calcule la inversa. \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)

3. Dada una transformación lineal \(T(\mathbf{x}) = \mathbf{Ax}\), explique cómo se transforman los vectores base \(\mathbf{e_1} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) y \(\mathbf{e_2} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}\), y visualice el resultado. (Donde, \(\mathbf{A} = \begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix}\))

4. Calcule el rango (rank) de la siguiente matriz. \(\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\)

Avanzado

1. Escriba la definición de descomposición en valores singulares (Singular Value Decomposition, SVD) y realice la descomposición SVD de la matriz dada. \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}\)

2. Explique el objetivo y el proceso del análisis de componentes principales (Principal Component Analysis, PCA) y realice un PCA en el conjunto de datos dado para reducir la dimensionalidad a una dimensión.

   import numpy as np
   data = np.array([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]])

3. Encuentre las bases del espacio nulo (null space) y del espacio de columnas (column space) de la siguiente matriz. \(\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\)

4. Escriba la definición de descomposición QR y realice la descomposición QR de la matriz dada. (La descomposición QR es un método numéricamente estable que se usa para encontrar soluciones a ecuaciones lineales o resolver problemas de valores propios.) \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)

Haga clic para ver el contenido (solución)

Soluciones a los Ejercicios

1. Álgebra Lineal

Básico

1. Producto interno: \(\mathbf{a} \cdot \mathbf{b} = (1)(3) + (2)(4) = 3 + 8 = 11\)

2. Producto matriz-vector: \(\mathbf{Ab} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 5 \\ 6 \end{bmatrix} = \begin{bmatrix} (1)(5) + (2)(6) \\ (3)(5) + (4)(6) \end{bmatrix} = \begin{bmatrix} 17 \\ 39 \end{bmatrix}\)

3. Matriz identidad 2x2: \(\mathbf{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

4. Normas L1, L2:

   • Norma L1 (Distancia de Manhattan): \(||\mathbf{v}||_1 = \sum_{i} |v_i|\)
   • Norma L2 (Distancia Euclidiana): \(||\mathbf{v}||_2 = \sqrt{\sum_{i} v_i^2}\)

   \(\mathbf{v} = \begin{bmatrix} 3 \\ -4 \end{bmatrix}\) \(||\mathbf{v}||_1 = |3| + |-4| = 3 + 4 = 7\) \(||\mathbf{v}||_2 = \sqrt{(3)^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)

Aplicado

1. Valores propios, vectores propios: \(\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\)

   • Ecuación característica: \(\det(\mathbf{A} - \lambda\mathbf{I}) = 0\) \((2-\lambda)^2 - (1)(1) = 0\) \(\lambda^2 - 4\lambda + 3 = 0\) \((\lambda - 3)(\lambda - 1) = 0\) \(\lambda_1 = 3\), \(\lambda_2 = 1\)

   • Vector propio (λ = 3): \((\mathbf{A} - 3\mathbf{I})\mathbf{v} = 0\) \(\begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\) \(x = y\), \(\mathbf{v_1} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) (o cualquier múltiplo constante)

   • Vector propio (λ = 1): \((\mathbf{A} - \mathbf{I})\mathbf{v} = 0\) \(\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\) \(x = -y\), \(\mathbf{v_2} = \begin{bmatrix} -1 \\ 1 \end{bmatrix}\) (o cualquier múltiplo constante)

2. Matriz inversa: \(\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)

• Determinación de existencia: \(\det(\mathbf{A}) = (1)(4) - (2)(3) = 4 - 6 = -2 \neq 0\). Existe la matriz inversa.
  • Cálculo de la matriz inversa: \(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \begin{bmatrix} 4 & -2 \\ -3 & 1 \end{bmatrix} = \frac{1}{-2} \begin{bmatrix} 4 & -2 \\ -3 & 1 \end{bmatrix} = \begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \end{bmatrix}\)

3. Visualización de la transformación lineal:
   • \(T(\mathbf{e_1}) = \mathbf{A}\mathbf{e_1} = \begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}\)
   • \(T(\mathbf{e_2}) = \mathbf{A}\mathbf{e_2} = \begin{bmatrix} 2 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} -1 \\ 1 \end{bmatrix}\)
   • Visualización: Se trazan en el plano de coordenadas las transformaciones de los vectores base originales \(\mathbf{e_1}\), \(\mathbf{e_2}\) a \(\begin{bmatrix} 2 \\ 1 \end{bmatrix}\), \(\begin{bmatrix} -1 \\ 1 \end{bmatrix}\) respectivamente.
4. Cálculo del rango: \(\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\) Al convertirlo a la forma escalonada por filas, dos filas tienen valores no nulos, por lo que el rango es 2. (La tercera fila puede expresarse como una combinación lineal de la primera y segunda filas)

Ampliación

1. SVD: \(\mathbf{A} = \mathbf{U\Sigma V^T}\)

   • \(\mathbf{U}\): Matriz ortogonal que tiene los vectores propios de \(\mathbf{A}\mathbf{A}^T\) como columnas
   • \(\mathbf{\Sigma}\): Matriz diagonal con los valores singulares (raíces cuadradas de los valores propios de \(\mathbf{A}\mathbf{A}^T\)) en la diagonal principal
   • \(\mathbf{V}\): Matriz ortogonal que tiene los vectores propios de \(\mathbf{A}^T\mathbf{A}\) como columnas

   (Se omite el proceso de cálculo. Es posible calcularlo usando bibliotecas como NumPy: U, S, V = np.linalg.svd(A))

2. PCA:

   ```python import numpy as np

   data = np.array([[1, 2], [2, 3], [3, 4], [4, 5], [5, 6]])

   1. Centrar los datos (restar la media)

   mean = np.mean(data, axis=0) centered_data = data - mean

   2. Calcular la matriz de covarianza

   covariance_matrix = np.cov(centered_data.T)

   3. Calcular los valores propios y vectores propios

   eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)

   4. Seleccionar componentes principales (vector propio correspondiente al mayor valor propio)

   Ordenar los valores propios en orden descendente y seleccionar el vector propio correspondiente al mayor valor propio

   sorted_indices = np.argsort(eigenvalues)[::-1] # Índices de ordenación descendente largest_eigenvector = eigenvectors[:, sorted_indices[0]] # 5. Proyección a una dimensión projected_data = centered_data.dot(largest_eigenvector)

print(projected_data)

3. **Espacios nulo y columna:**
$\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$

*   **Espacio nulo (Null Space):** Encontrar $\mathbf{x}$ que satisface $\mathbf{Ax} = 0$.
    Al transformar a forma escalonada reducida, la solución es:
    $\mathbf{x} = t\begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}$ (t es una constante arbitraria).
    Por lo tanto, la base del espacio nulo es $\begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}$

*   **Espacio columna (Column Space):** Espacio generado por las combinaciones lineales de los vectores columna de la matriz $\mathbf{A}$.
    Los vectores columna correspondientes a las columnas pivote en la forma escalonada reducida son bases.
    $\begin{bmatrix} 1 \\ 4 \\ 7 \end{bmatrix}$, $\begin{bmatrix} 2 \\ 5 \\ 8 \end{bmatrix}$

4. **Descomposición QR:**
$\mathbf{A} = \mathbf{QR}$
*   $\mathbf{Q}$: Matriz con vectores columna ortonormales
*   $\mathbf{R}$: Matriz triangular superior (upper triangular matrix)

(El proceso de cálculo puede usar el proceso de ortogonalización de Gram-Schmidt o bibliotecas como NumPy para calcular: `Q, R = np.linalg.qr(A)`)
:::

## Ejercicios de práctica

### 2 Cálculo y optimización

#### Básico

1.  Encuentre la derivada $f'(x)$ de la función $f(x) = x^3 - 6x^2 + 9x + 1$.

2.  Encuentre las derivadas parciales $\frac{\partial f}{\partial x}$ y $\frac{\partial f}{\partial y}$ de la función $f(x, y) = x^2y + 2xy^2$.

3.  Utilice la regla de la cadena para encontrar la derivada $f'(x)$ de la función $f(x) = \sin(x^2)$.

#### Aplicado

1.  Encuentre el gradiente $\nabla f$ de la función $f(x, y) = e^{x^2 + y^2}$ y calcule su valor en el punto (1, 1).

2.  Encuentre todos los puntos críticos de la función $f(x) = x^4 - 4x^3 + 4x^2$ y determine si cada uno es un máximo local, un mínimo local o un punto de silla.

3.  Encuentre la matriz jacobiana de la siguiente función:
    $f(x, y) = \begin{bmatrix} x^2 + y^2 \\ 2xy \end{bmatrix}$

#### Avanzado

1.  Utilice el método de los multiplicadores de Lagrange para encontrar los valores máximos y mínimos de la función $f(x, y) = xy$ sujeta a la restricción $g(x, y) = x^2 + y^2 - 1 = 0$.

2.  Utilice el método del descenso por gradiente para encontrar el mínimo de la función $f(x) = x^4 - 4x^3 + 4x^2$. (Valor inicial $x_0 = 3$, tasa de aprendizaje $\alpha = 0.01$, número de iteraciones 100)

3.  Expresione el gradiente $\nabla f$ de la función $f(\mathbf{x}) = \mathbf{x}^T \mathbf{A} \mathbf{x}$ en términos de $\mathbf{A}$ y $\mathbf{x}$. (Donde $\mathbf{A}$ es una matriz simétrica)

4.  Utilice el método de Newton para encontrar las raíces de la ecuación $x^3 - 2x - 5 = 0$.

::: {.callout-note collapse="true" title="Haga clic para ver el contenido (solución)"}
## Soluciones de problemas de práctica

### 2 Cálculo y optimización

#### Básico

1.  **Derivada:**
    $f(x) = x^3 - 6x^2 + 9x + 1$
    $f'(x) = 3x^2 - 12x + 9$

2.  **Derivadas parciales:**
    $f(x, y) = x^2y + 2xy^2$
    $\frac{\partial f}{\partial x} = 2xy + 2y^2$
    $\frac{\partial f}{\partial y} = x^2 + 4xy$

3.  **Regla de la cadena:**
    $f(x) = \sin(x^2)$
    $f'(x) = \cos(x^2) \cdot (2x) = 2x\cos(x^2)$

#### Aplicado

1.  **Gradiente:**
    $f(x, y) = e^{x^2 + y^2}$
    $\nabla f = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} = \begin{bmatrix} 2xe^{x^2 + y^2} \\ 2ye^{x^2 + y^2} \end{bmatrix}$
    $\nabla f(1, 1) = \begin{bmatrix} 2e^2 \\ 2e^2 \end{bmatrix}$

2.  **Puntos críticos, clasificación de valores extremos:**
    $f(x) = x^4 - 4x^3 + 4x^2$
    $f'(x) = 4x^3 - 12x^2 + 8x = 4x(x-1)(x-2)$
    Puntos críticos: $x = 0, 1, 2$

    $f''(x) = 12x^2 - 24x + 8$
    *   $f''(0) = 8 > 0$: mínimo local
    *   $f''(1) = -4 < 0$: máximo local
    *   $f''(2) = 8 > 0$: mínimo local

3.  **Matriz jacobiana:**
    $f(x, y) = \begin{bmatrix} x^2 + y^2 \\ 2xy \end{bmatrix}$
    $\mathbf{J} = \begin{bmatrix} \frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \\ \frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} \end{bmatrix} = \begin{bmatrix} 2x & 2y \\ 2y & 2x \end{bmatrix}$

#### Avanzado

1.  **Método de multiplicadores de Lagrange:**
    $L(x, y, \lambda) = xy - \lambda(x^2 + y^2 - 1)$
    $\frac{\partial L}{\partial x} = y - 2\lambda x = 0$
    $\frac{\partial L}{\partial y} = x - 2\lambda y = 0$
    $\frac{\partial L}{\partial \lambda} = x^2 + y^2 - 1 = 0$

    *   $x = \pm \frac{1}{\sqrt{2}}$, $y = \pm \frac{1}{\sqrt{2}}$, $\lambda = \pm \frac{1}{2}$
    *   Máximo: $f(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = f(-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) = \frac{1}{2}$
    *   Mínimo: $f(\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}) = f(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) = -\frac{1}{2}$

2.  **Descenso por gradiente:**

    ```python
    def gradient_descent(f, df, x0, alpha, iterations):
        x = x0
        for i in range(iterations):
            x = x - alpha * df(x)
        return x
    ```
f = lambda x: x**4 - 4*x**3 + 4*x**2
df = lambda x: 4*x**3 - 12*x**2 + 8*x

x_min = gradient_descent(f, df, 3, 0.01, 100)
print(x_min) # converge aproximadamente a 2

3. Gradiente (en forma de matriz): \(f(\mathbf{x}) = \mathbf{x}^T \mathbf{A} \mathbf{x}\) \(\nabla f = (\mathbf{A} + \mathbf{A}^T)\mathbf{x}\). Como \(\mathbf{A}\) es una matriz simétrica, \(\nabla f = 2\mathbf{A}\mathbf{x}\)

4. Método de Newton: \(f(x) = x^3 - 2x - 5\) \(f'(x) = 3x^2 - 2\) \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\)

def newton_method(f, df, x0, iterations):
    x = x0
    for i in range(iterations):
        x = x - f(x) / df(x)
    return x

f = lambda x: x**3 - 2*x - 5
df = lambda x: 3*x**2 - 2

root = newton_method(f, df, 2, 5) # valor inicial x0 = 2, 5 iteraciones
print(root)

Ejercicios de práctica

3 Probabilidad y estadística

Básico

1. Calcule la probabilidad de que aparezca cara dos veces cuando se lanza una moneda tres veces.

2. Calcule la probabilidad de que salga un número par cuando se lanza un dado.

3. Escriba la función de densidad de probabilidad (PDF) de una distribución normal y explique el significado de la media y la varianza.

Aplicación

1. Explique el teorema de Bayes (Bayes’ theorem) y aplíquelo al siguiente problema.

   • Si la prevalencia de una enfermedad es del 1% y la precisión de la prueba diagnóstica (sensibilidad y especificidad) es del 99%, ¿cuál es la probabilidad de que realmente se tenga la enfermedad si el resultado de la prueba es positivo?

2. Explique el concepto de estimación de máxima verosimilitud (Maximum Likelihood Estimation, MLE) y calcule el MLE para la probabilidad de que aparezca cara cuando se lanza una moneda cinco veces y cae tres veces.

3. Escriba la definición de valor esperado (expectation) y escriba las fórmulas para calcular el valor esperado de variables aleatorias discretas y continuas, respectivamente.

Avanzado

1. Escriba la definición de entropía (entropy) y calcule la entropía para la siguiente distribución de probabilidad.

   • P(X=1) = 0.5, P(X=2) = 0.25, P(X=3) = 0.25

2. Si la distribución conjunta de probabilidad (joint probability distribution) de dos variables aleatorias X e Y es la siguiente, calcule la información mutua (mutual information) I(X;Y).

   P(X=0, Y=0) = 0.1, P(X=0, Y=1) = 0.2
   P(X=1, Y=0) = 0.3, P(X=1, Y=1) = 0.4

3. Si las distribuciones de probabilidad P y Q son las siguientes, calcule la divergencia KL (Kullback-Leibler divergence) \(D_{KL}(P||Q)\).

   • P(X=1) = 0.6, P(X=2) = 0.4
   • Q(X=1) = 0.8, Q(X=2) = 0.2

4. Escriba la función de masa de probabilidad (PMF) de la distribución de Poisson y dé un ejemplo de cuándo se utiliza.

Haga clic para ver el contenido (solución)

Soluciones de Ejercicios

3 Probabilidad y Estadística

Básico

1. Lanzamiento de Moneda: Probabilidad = (Número de casos en los que caen 2 caras en 3 lanzamientos) * (Probabilidad de cara)^2 * (Probabilidad de cruz)^1 = 3C2 * (1/2)^2 * (1/2)^1 = 3 * (1/4) * (1/2) = 3/8

2. Lanzamiento de Dados: Probabilidad = (Número de casos en los que cae un número par) / (Número total de casos) = 3 / 6 = 1/2

3. Distribución Normal: \(f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)

   • \(\mu\): Media (centro de la distribución)
   • \(\sigma\): Desviación estándar (dispersión de la distribución)

Aplicaciones

1. Teorema de Bayes: \(P(A|B) = \frac{P(B|A)P(A)}{P(B)}\)

   • \(P(A)\): Probabilidad de tener una enfermedad (probabilidad a priori) = 0.01
   • \(P(B|A)\): Probabilidad de que la prueba sea positiva si se tiene la enfermedad (sensibilidad) = 0.99
   • \(P(B|\neg A)\): Probabilidad de que la prueba sea positiva si no se tiene la enfermedad (1 - especificidad) = 0.01 (asumiendo una especificidad de 0.99)
   • \(P(B)\): Probabilidad de que la prueba sea positiva = \(P(B|A)P(A) + P(B|\neg A)P(\neg A) = (0.99)(0.01) + (0.01)(0.99) = 0.0198\)

   \(P(A|B) = \frac{(0.99)(0.01)}{0.0198} = 0.5\) (50%)

2. Estimación de Máxima Verosimilitud (MLE):

• Función de verosimilitud: \(L(p) = p^3 (1-p)^2\) (p es la probabilidad de que caiga cara)
  • Derivada: \(\frac{dL}{dp} = 3p^2(1-p)^2 - 2p^3(1-p)\)
  • Igualando a cero y resolviendo para p, se obtiene \(p = \frac{3}{5}\)

3. Divergencia de Kullback-Leibler: \(D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\)

Avanzado

1. Entropía: Entropía es una medida de la incertidumbre, desorden o cantidad de información en una distribución de probabilidad. \(H(P) = -\sum_{x} P(x) \log P(x)\) (la base del logaritmo suele ser 2 o el logaritmo natural e)

   \(H(P) = -(0.5 \log 0.5 + 0.25 \log 0.25 + 0.25 \log 0.25)\) (usando logaritmos de base 2) \(H(P) \approx 1.5\) bits

2. Información Mutua: \(I(X;Y) = \sum_{x}\sum_{y} P(x,y) \log \frac{P(x,y)}{P(x)P(y)}\)

   • \(P(X=0) = 0.1 + 0.2 = 0.3\)
   • \(P(X=1) = 0.3 + 0.4 = 0.7\)
   • \(P(Y=0) = 0.1 + 0.3 = 0.4\)
   • \(P(Y=1) = 0.2 + 0.4 = 0.6\)

   \(I(X;Y) = (0.1)\log\frac{0.1}{(0.3)(0.4)} + (0.2)\log\frac{0.2}{(0.3)(0.6)} + (0.3)\log\frac{0.3}{(0.7)(0.4)} + (0.4)\log\frac{0.4}{(0.7)(0.6)}\) \(I(X;Y) \approx 0.0867\) (usando logaritmos de base 2)

3. Divergencia KL: \(D_{KL}(P||Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}\) \(D_{KL}(P||Q) = 0.6 \log \frac{0.6}{0.8} + 0.4 \log \frac{0.4}{0.2} \approx 0.083\)

4. Distribución de Poisson:

   • Función de masa de probabilidad (PMF): \(P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}\) (\(k\) es el número de ocurrencias, \(\lambda\) es la tasa media de ocurrencia por unidad de tiempo/espacio)
   • Ejemplos de uso:
     • Número de llamadas recibidas en un centro de llamadas durante un período específico
     • Número de accidentes de tráfico ocurridos en una zona específica
     • Número de errores tipográficos encontrados en un libro
     • Número de visitantes que acceden a un sitio web
     • Desintegración radiactiva, mutaciones genéticas

Referencias

Materiales esenciales de referencia

1. Linear Algebra and Its Applications (Gilbert Strang, 4th Edition):
   • Este es un libro de texto que cubre los conceptos básicos y aplicaciones del álgebra lineal. Explica claramente el contenido esencial necesario para el aprendizaje profundo.
   • Curso de Álgebra Lineal de Gilbert Strang (MIT OCW)
2. Calculus (James Stewart, 8th Edition):
   • Este libro de texto explica detalladamente los principios básicos del cálculo. Proporciona el conocimiento previo necesario para comprender los algoritmos de optimización en el aprendizaje profundo.
3. Probability and Statistics for Engineering and the Sciences (Jay L. Devore, 9th Edition):
   • Este libro de texto explica los conceptos básicos de probabilidad y estadística junto con aplicaciones ingenieriles. Ayuda a comprender la modelización probabilística y la inferencia de incertidumbre en el aprendizaje profundo.
4. Pattern Recognition and Machine Learning (Christopher Bishop):
   • Este es un libro de texto clásico sobre reconocimiento de patrones y aprendizaje automático. Aborda a fondo los temas teóricos del aprendizaje profundo, como la modelización probabilística, la inferencia bayesiana y la teoría de la información.
5. The Elements of Statistical Learning (Trevor Hastie, Robert Tibshirani, Jerome Friedman):
   • Este libro de texto explica claramente los conceptos clave de la teoría del aprendizaje estadístico. Es útil para comprender el rendimiento generalizador y los problemas de sobreajuste en los modelos de aprendizaje profundo.
   • The Elements of Statistical Learning (PDF gratuito)
6. Deep Learning (Ian Goodfellow, Yoshua Bengio, Aaron Courville):
   • Este es un libro de texto que abarca los conceptos básicos y las técnicas más recientes del aprendizaje profundo. Introduce brevemente la base matemática necesaria para el aprendizaje profundo.
   • Deep Learning Book (PDF gratuito)
7. Understanding Machine Learning: From Theory to Algorithms (Shai Shalev-Shwartz, Shai Ben-David):
   • Este libro de texto proporciona una base sólida en la teoría del aprendizaje automático. Explica conceptos importantes para comprender el rendimiento generalizador de los modelos de aprendizaje profundo, como la teoría PAC, la dimensión VC y el compromiso sesgo-varianza.
8. Information Theory, Inference, and Learning Algorithms (David J.C. MacKay):
   • Este libro de texto explica los principios del aprendizaje automático centrados en la teoría de la información y la inferencia bayesiana. Ayuda a comprender la interpretación probabilística y los modelos generativos en el aprendizaje profundo.
   • Information Theory, Inference, and Learning Algorithms (PDF gratuito)
9. Mathematics for Machine Learning (Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong)
   • Este libro de texto aborda ampliamente los conocimientos matemáticos necesarios para el aprendizaje automático.
10. Matrix Computations (Gene H. Golub, Charles F. Van Loan, 4th Edition):
    • Este libro de texto trata exhaustivamente métodos numéricos relacionados con operaciones de matrices. Proporciona el conocimiento necesario para implementar y mejorar los algoritmos de optimización en el aprendizaje profundo.
11. Linear Algebra and Its Applications (Gilbert Strang, 4th Edition):
    • Libro de texto que aborda los conceptos básicos y aplicaciones del álgebra lineal. Explica claramente el contenido esencial para el aprendizaje profundo. - Curso de Álgebra Lineal de Gilbert Strang (MIT OCW)
12. Calculus (James Stewart, 8th Edition):
    • Libro de texto que explica detalladamente los principios básicos del cálculo. Proporciona el conocimiento de fondo necesario para comprender los algoritmos de optimización en el aprendizaje profundo.
13. Probability and Statistics for Engineering and the Sciences (Jay L. Devore, 9th Edition):
    • Libro de texto que explica los conceptos básicos de probabilidad y estadística junto con sus aplicaciones ingenieriles. Ayuda a comprender la modelización probabilística y la inferencia de incertidumbre en el aprendizaje profundo.
14. Pattern Recognition and Machine Learning (Christopher Bishop):
    • Libro de texto clásico sobre reconocimiento de patrones y aprendizaje automático. Aborda profundamente los conceptos teóricos del aprendizaje profundo, incluyendo modelización probabilística, inferencia bayesiana e información teórica.
15. The Elements of Statistical Learning (Trevor Hastie, Robert Tibshirani, Jerome Friedman):
    • Libro de texto que explica claramente los conceptos clave de la teoría del aprendizaje estadístico. Es útil para comprender el rendimiento generalizado y los problemas de sobreajuste en los modelos de aprendizaje profundo. - The Elements of Statistical Learning (Free PDF)
16. Deep Learning (Ian Goodfellow, Yoshua Bengio, Aaron Courville):
    • Libro de texto que abarca exhaustivamente los conceptos básicos y las tecnologías más recientes del aprendizaje profundo. Introduce brevemente la base matemática necesaria para el aprendizaje profundo. - Libro de Aprendizaje Profundo (Free PDF)
17. Understanding Machine Learning: From Theory to Algorithms (Shai Shalev-Shwartz, Shai Ben-David):
    • Libro de texto que establece firmemente los fundamentos teóricos del aprendizaje automático. Explica conceptos importantes para comprender el rendimiento generalizado de los modelos de aprendizaje profundo, como la teoría PAC, la dimensión VC y el trade-off sesgo-varianza.
18. Information Theory, Inference, and Learning Algorithms (David J.C. MacKay):
    • Libro de texto que explica los principios del aprendizaje automático centrados en la teoría de la información y la inferencia bayesiana. Ayuda a comprender la interpretación probabilística y los modelos generativos en el aprendizaje profundo. - Information Theory, Inference, and Learning Algorithms (Free PDF)
19. Mathematics for Machine Learning (Marc Peter Deisenroth, A. Aldo Faisal, y Cheng Soon Ong)
    • Aborda ampliamente el conocimiento matemático necesario para el aprendizaje automático.
20. Matrix Computations (Gene H. Golub, Charles F. Van Loan, 4th Edition): - Es un libro de texto que trata profundamente los métodos numéricos relacionados con las operaciones matriciales. Proporciona el conocimiento necesario para implementar y mejorar el rendimiento de los algoritmos de optimización en deep learning.