Code
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local
%load_ext autoreload
%autoreload 2“Attention is all you need.” - Ashish Vaswani et al., NeurIPS 2017.
2017 fue un año especial en la historia del procesamiento de lenguaje natural. Esto se debe a que Google presentó el Transformer en su artículo “Attention is All You Need”. Este avance es comparable a la revolución que AlexNet trajo al reconocimiento visual en 2012. Con la aparición del Transformer, el procesamiento de lenguaje natural (NLP) entró en una nueva era. A partir de entonces, surgieron modelos de lenguaje poderosos basados en Transformers, como BERT y GPT, abriendo un nuevo capítulo en la historia de la inteligencia artificial.
Notas
El Capítulo 8 reconstruye el proceso de desarrollo del Transformer por parte del equipo de investigación de Google de manera dramática. Basándose en el artículo original, blogs de investigación, presentaciones académicas y otros materiales, se ha intentado describir vividamente las preocupaciones y procesos de resolución de problemas que los investigadores podrían haber enfrentado. En este proceso, se aclara que algunas partes han sido reconstruidas con base en razonamientos y imaginación razonables.
Desafío: ¿Cómo superar las limitaciones fundamentales de los modelos basados en redes neuronales recurrentes (RNN)?
Angustia del investigador: En ese momento, los modelos basados en RNN, LSTM y GRU eran dominantes en el campo del procesamiento de lenguaje natural. Sin embargo, estos modelos tenían que procesar secuencias de entrada de manera secuencial, lo que hacía imposible la paralelización y provocaba problemas de dependencia a largo plazo al procesar oraciones largas. Los investigadores necesitaban superar estas limitaciones fundamentales y desarrollar una nueva arquitectura que fuera más rápida, eficiente y capaz de comprender mejor contextos extensos.
El procesamiento de lenguaje natural había estado atrapado durante mucho tiempo en las limitaciones del procesamiento secuencial. El procesamiento secuencial implica procesar una oración palabra por palabra o token a token en orden. Al igual que cómo los humanos leen un texto palabra por palabra, RNN y LSTM también tenían que procesar la entrada de manera secuencial. Este tipo de procesamiento secuencial presentaba dos problemas graves: 1) no se podía aprovechar eficientemente el hardware de procesamiento paralelo como GPUs, y 2) al procesar oraciones largas, la información del comienzo (palabras) no se transmitía adecuadamente a las partes posteriores, conocido como el “problema de dependencia a largo plazo (long-range dependency problem)”. En otras palabras, cuando los elementos relacionados dentro de una oración estaban muy separados, no podían ser procesados correctamente.
El mecanismo de atención, que apareció en 2014, resolvió parcialmente estos problemas. A diferencia de RNN tradicionales, donde el decodificador solo consultaba el último estado oculto del codificador, la atención permitía al decodificador considerar todos los estados ocultos del codificador. Sin embargo, aún había limitaciones fundamentales. La estructura misma de RNN estaba basada en el procesamiento secuencial, por lo que seguían teniendo que procesar una palabra a la vez. Como resultado, no era posible realizar un procesamiento paralelo con GPUs y, por lo tanto, el tiempo de procesamiento para secuencias largas era considerable.
En 2017, el equipo de investigación de Google desarrolló el Transformer para mejorar significativamente el rendimiento en traducción automática. El Transformer resolvió estas limitaciones fundamentales al eliminar completamente las RNN y adoptar un enfoque basado únicamente en la atención propia (self-attention).
El Transformer tiene tres ventajas clave: 1. Procesamiento paralelo: puede procesar todas las posiciones de una secuencia simultáneamente, maximizando el uso de GPUs. 2. Dependencia global: todos los tokens pueden definir directamente la intensidad de su relación con todos los demás tokens. 3. Manejo flexible de la información de posición: a través del codificado posicional, representa eficazmente la información de orden mientras se adapta flexiblemente a secuencias de diferentes longitudes. El transformer pronto se convirtió en la base de potentes modelos de lenguaje como BERT y GPT, e incluso se expandió a otros campos, como el Vision Transformer. El transformer no fue solo una nueva arquitectura simple, sino que llevó a un replanteamiento fundamental del procesamiento de información en el deep learning. En particular, esto condujo al éxito de ViT (Vision Transformer) en el campo de la visión por computadora, convirtiéndose en un fuerte competidor para las CNN.
A principios de 2017, el equipo de investigación de Google se encontró con un obstáculo en el campo de la traducción automática. En ese momento, los modelos secuencia a secuencia (seq-to-seq) basados en RNN, que eran predominantes, tenían un problema crónico: su rendimiento disminuía significativamente al procesar oraciones largas. Aunque el equipo de investigación hizo esfuerzos multidireccionales para mejorar la estructura del RNN, estos solo fueron medidas temporales y no una solución fundamental. En medio de este desafío, un investigador puso su atención en el mecanismo de atención publicado en 2014 (Bahdanau et al., 2014). “Si la atención había mitigado el problema de las dependencias a larga distancia, ¿no sería posible procesar secuencias solo con atención, sin necesidad de RNN?”
Muchas personas experimentan confusión al conocer por primera vez el mecanismo de atención, especialmente en los conceptos de Q, K y V. De hecho, la forma inicial de la atención se presentó como “puntuación de alineamiento” en el artículo de Bahdanau de 2014. Esta puntuación indicaba qué parte del codificador debía enfocar el decodificador al generar una palabra de salida y, esencialmente, era un valor que representaba la correlación entre dos vectores.
Es probable que el equipo de investigación haya comenzado con la pregunta práctica: “¿Cómo se pueden cuantificar las relaciones entre palabras?”. Empezaron con la idea relativamente simple de calcular la similitud entre vectores y usar estos valores como pesos para sintetizar información contextual. De hecho, en los primeros documentos de diseño del equipo de investigación de Google (“Transformers: Iterative Self-Attention and Processing for Various Tasks”), se utilizaba un método similar a “puntuación de alineamiento” para representar las relaciones entre palabras, en lugar de los términos Q, K y V.
A continuación, seguiremos el proceso que los investigadores de Google siguieron para resolver el problema y entenderemos el mecanismo de atención. Comenzaremos con la idea básica de calcular la similitud entre vectores y explicaremos paso a paso cómo llegaron a completar finalmente la arquitectura del Transformer.
El equipo de investigación primero quiso comprender claramente los límites del RNN. A través de experimentos, confirmaron que a medida que aumentaba la longitud de las oraciones, especialmente cuando superaban las 50 palabras, la puntuación BLEU disminuía drásticamente. Un problema aún mayor era que, debido al procesamiento secuencial del RNN, incluso con el uso de GPU, era difícil mejorar significativamente la velocidad. Para superar estas limitaciones, el equipo realizó un análisis profundo del mecanismo de atención propuesto por Bahdanau et al. (2014). La atención permitía que el decodificador consultara todos los estados del codificador, lo que mitigaba el problema de las dependencias a larga distancia. A continuación se presenta una implementación básica del mecanismo de atención.
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local
%load_ext autoreload
%autoreload 2import numpy as np
# Example word vectors (3-dimensional)
word_vectors = {
'time': np.array([0.2, 0.8, 0.3]), # In reality, these would be hundreds of dimensions
'flies': np.array([0.7, 0.2, 0.9]),
'like': np.array([0.3, 0.5, 0.2]),
'an': np.array([0.1, 0.3, 0.4]),
'arrow': np.array([0.8, 0.1, 0.6])
}
def calculate_similarity_matrix(word_vectors):
"""Calculates the similarity matrix between word vectors."""
X = np.vstack(list(word_vectors.values()))
return np.dot(X, X.T)The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreloadEl contenido explicado en esta sección proviene del documento de diseño inicial “Transformers: Iterative Self-Attention and Processing for Various Tasks”. A continuación, analizaremos paso a paso el código utilizado para explicar los conceptos básicos de la atención. Primero, solo consideremos la matriz de similitud (pasos 1 y 2 del código fuente). Las palabras suelen tener cientos de dimensiones. Aquí, por ejemplo, se representan con vectores de 3 dimensiones. Cuando se forman en una matriz, cada columna es un vector de palabra. Al transponer esta matriz, los vectores de palabra se convierten en vectores fila. Al realizar la operación entre estas dos matrices, cada elemento (i, j) representa el producto escalar entre el i-ésimo y el j-ésimo vector de palabra, lo que indica la distancia (similitud) entre las dos palabras.
import numpy as np
def visualize_similarity_matrix(words, similarity_matrix):
"""Visualizes the similarity matrix in ASCII art format."""
max_word_len = max(len(word) for word in words)
col_width = max_word_len + 4
header = " " * (col_width) + "".join(f"{word:>{col_width}}" for word in words)
print(header)
for i, word in enumerate(words):
row_str = f"{word:<{col_width}}"
row_values = [f"{similarity_matrix[i, j]:.2f}" for j in range(len(words))]
row_str += "".join(f"[{value:>{col_width-2}}]" for value in row_values)
print(row_str)
# Example word vectors (in practice, these would have hundreds of dimensions)
word_vectors = {
'time': np.array([0.2, 0.8, 0.3]),
'flies': np.array([0.7, 0.2, 0.9]),
'like': np.array([0.3, 0.5, 0.2]),
'an': np.array([0.1, 0.3, 0.4]),
'arrow': np.array([0.8, 0.1, 0.6])
}
words = list(word_vectors.keys()) # Preserve order
# 1. Convert word vectors into a matrix
X = np.vstack([word_vectors[word] for word in words])
# 2. Calculate the similarity matrix (dot product)
similarity_matrix = calculate_similarity_matrix(word_vectors)
# Print results
print("Input matrix shape:", X.shape)
print("Input matrix:\n", X)
print("\nInput matrix transpose:\n", X.T)
print("\nSimilarity matrix shape:", similarity_matrix.shape)
print("Similarity matrix:") # Output from visualize_similarity_matrix
visualize_similarity_matrix(words, similarity_matrix)Input matrix shape: (5, 3)
Input matrix:
[[0.2 0.8 0.3]
[0.7 0.2 0.9]
[0.3 0.5 0.2]
[0.1 0.3 0.4]
[0.8 0.1 0.6]]
Input matrix transpose:
[[0.2 0.7 0.3 0.1 0.8]
[0.8 0.2 0.5 0.3 0.1]
[0.3 0.9 0.2 0.4 0.6]]
Similarity matrix shape: (5, 5)
Similarity matrix:
time flies like an arrow
time [ 0.77][ 0.57][ 0.52][ 0.38][ 0.42]
flies [ 0.57][ 1.34][ 0.49][ 0.49][ 1.12]
like [ 0.52][ 0.49][ 0.38][ 0.26][ 0.41]
an [ 0.38][ 0.49][ 0.26][ 0.26][ 0.35]
arrow [ 0.42][ 1.12][ 0.41][ 0.35][ 1.01]Por ejemplo, el valor del elemento (1,2) de la matriz de similitud 0.57 representa la distancia (similitud) entre los vectores de times en el eje de las filas y flies en el eje de las columnas. Esto se puede expresar matemáticamente de la siguiente manera.
\(\mathbf{X} = \begin{bmatrix} \mathbf{x_1} \\ \mathbf{x_2} \\ \vdots \\ \mathbf{x_n} \end{bmatrix}\)
\(\mathbf{X}^T = \begin{bmatrix} \mathbf{x_1}^T & \mathbf{x_2}^T & \cdots & \mathbf{x_n}^T \end{bmatrix}\)
\(\mathbf{X}\mathbf{X}^T = \begin{bmatrix} \mathbf{x_1} \cdot \mathbf{x_1} & \mathbf{x_1} \cdot \mathbf{x_2} & \cdots & \mathbf{x_1} \cdot \mathbf{x_n} \\ \mathbf{x_2} \cdot \mathbf{x_1} & \mathbf{x_2} \cdot \mathbf{x_2} & \cdots & \mathbf{x_2} \cdot \mathbf{x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{x_n} \cdot \mathbf{x_1} & \mathbf{x_n} \cdot \mathbf{x_2} & \cdots & \mathbf{x_n} \cdot \mathbf{x_n} \end{bmatrix}\)
\((\mathbf{X}\mathbf{X}^T)_{ij} = \mathbf{x_i} \cdot \mathbf{x_j} = \sum_{k=1}^d x_{ik}x_{jk}\)
Cada elemento de esta matriz n×n es el producto escalar entre dos vectores de palabras, y por lo tanto representa la distancia (similitud) entre las dos palabras. Esto son los “puntajes de atención”.
El siguiente es el paso de convertir la matriz de similitud en una matriz de pesos utilizando el softmax, que consta de 3 etapas.
# 3. Convert similarities to weights (probability distribution) (softmax)
def softmax(x):
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True)) # trick for stability
return exp_x / exp_x.sum(axis=-1, keepdims=True)
attention_weights = softmax(similarity_matrix)
print("Attention weights shape:", attention_weights.shape)
print("Attention weights:\n", attention_weights)Attention weights shape: (5, 5)
Attention weights:
[[0.25130196 0.20574865 0.19571417 0.17014572 0.1770895 ]
[0.14838442 0.32047566 0.13697608 0.13697608 0.25718775]
[0.22189237 0.21533446 0.19290396 0.17109046 0.19877876]
[0.20573742 0.22966017 0.18247272 0.18247272 0.19965696]
[0.14836389 0.29876818 0.14688764 0.13833357 0.26764673]]Los pesos de atención se aplican utilizando la función softmax. Realizan dos transformaciones clave:
Al convertir la matriz de similitud en pesos, se expresa probabilísticamente la relevancia de una palabra con respecto a las demás palabras. Dado que tanto los ejes de filas como columnas siguen el orden de las palabras en la oración, la primera fila de pesos corresponde a la fila de la palabra ‘time’, y las columnas representan todas las palabras de la oración. Por lo tanto,
Estos pesos transformados se utilizan en el siguiente paso para ponderar la oración. Al aplicar estas ponderaciones, cada palabra de la oración refleja cuánta información contiene. Esto equivale a decidir qué tan atentas deben ser las palabras al “referirse” a la información de otras palabras.
# 4. Generate contextualized representations using the weights
contextualized_vectors = np.dot(attention_weights, X)
print("\nContextualized vectors shape:", contextualized_vectors.shape)
print("Contextualized vectors:\n", contextualized_vectors)
Contextualized vectors shape: (5, 3)
Contextualized vectors:
[[0.41168487 0.40880105 0.47401919]
[0.51455048 0.31810231 0.56944172]
[0.42911583 0.38823778 0.48665295]
[0.43462426 0.37646585 0.49769319]
[0.51082753 0.32015331 0.55869952]]El producto punto entre la matriz de pesos y la matriz de palabras (compuesta por vectores de palabras) necesita una interpretación. Si asumimos que la primera fila de attention_weights es [0.5, 0.2, 0.1, 0.1, 0.1], cada valor representa la probabilidad de relevancia de ‘time’ con las demás palabras. La primera fila de pesos puede expresarse como \(\begin{bmatrix} \alpha_{11} & \alpha_{12} & \alpha_{13} & \alpha_{14} & \alpha_{15} \end{bmatrix}\), por lo que la operación con la matriz de palabras para esta fila de pesos se puede expresar así:
\(\begin{bmatrix} \alpha_{11} & \alpha_{12} & \alpha_{13} & \alpha_{14} & \alpha_{15} \end{bmatrix} \begin{bmatrix} \vec{v}_{\text{time}} \ \vec{v}_{\text{flies}} \ \vec{v}_{\text{like}} \ \vec{v}_{\text{an}} \ \vec{v}_{\text{arrow}} \end{bmatrix}\)
Esto se puede representar en código Python de la siguiente manera.
time_contextualized = 0.5*time_vector + 0.2*flies_vector + 0.1*like_vector + 0.1*an_vector + 0.1*arrow_vector
# 0.5는 time과 time의 관련도 확률값
# 0.2는 time과 files의 관련도 확률값La operación multiplica estas probabilidades (donde el tiempo está relacionado con la probabilidad de cada palabra) por los vectores originales de cada palabra y luego suma todos. Como resultado, el nuevo vector de ‘time’ refleja un promedio ponderado de los significados de las otras palabras, según su relevancia. El punto clave es que se calcula un promedio ponderado. Por lo tanto, fue necesario un paso previo para obtener la matriz de pesos que se utiliza para calcular el promedio ponderado.
La forma del vector contextualizado final es (5, 3), ya que esto resulta de multiplicar una matriz de pesos de atención de tamaño (5,5) por una matriz de vectores de palabras X de tamaño (5,3), lo que da como resultado (5,5) @ (5,3) = (5,3).
Sure, please provide the Korean text you want to be translated into Spanish.
El equipo de investigación de Google analizó el mecanismo de atención básico (sección 8.2.2) y descubrió varias limitaciones. El problema más importante era que los vectores de palabras realizaban tareas múltiples, como el cálculo de similitud y la transmisión de información, lo cual resultaba ineficiente. Por ejemplo, la palabra “bank” puede tener significados diferentes según el contexto, como “banco” o “orilla del río”, y por lo tanto, sus relaciones con otras palabras también deben ser diferentes. Sin embargo, un único vector no podía representar adecuadamente estos diversos significados y relaciones.
El equipo buscó una forma de optimizar cada rol de manera independiente. Esto se asemeja a cómo en las CNN, los filtros aprenden a extraer características de imágenes de manera aprendible, permitiendo que en el mecanismo de atención, cada rol tenga representaciones aprendidas especializadas. Esta idea comenzó con la transformación de los vectores de palabras en espacios para diferentes roles.
Limitaciones del concepto básico (ejemplo de código)
def basic_self_attention(word_vectors):
similarity_matrix = np.dot(word_vectors, word_vectors.T)
attention_weights = softmax(similarity_matrix)
contextualized_vectors = np.dot(attention_weights, word_vectors)
return contextualized_vectorsEn el siguiente código, word_vectors cumple tres roles simultáneos:
Primer mejoramiento: Separación del rol de transmisión de información
El equipo de investigación primero separó el rol de transmisión de información. El método más simple para separar los roles de un vector en álgebra lineal es usar una matriz de aprendizaje separada para realizar una transformación lineal (linear transformation) del vector a un nuevo espacio.
def improved_self_attention(word_vectors, W_similarity, W_content):
similarity_vectors = np.dot(word_vectors, W_similarity)
content_vectors = np.dot(word_vectors, W_content)
# Calculate similarity by taking the dot product between similarity_vectors
attention_scores = np.dot(similarity_vectors, similarity_vectors.T)
# Convert to probability distribution using softmax
attention_weights = softmax(attention_scores)
# Generate the final contextualized representation by multiplying weights and content_vectors
contextualized_vectors = np.dot(attention_weights, content_vectors)
return contextualized_vectorsW_similarity: matriz aprendible que proyecta los vectores de palabras a un espacio optimizado para el cálculo de similitud.W_content: matriz aprendible que proyecta los vectores de palabras a un espacio optimizado para la transmisión de información.Con esta mejora, similarity_vectors se especializó en el cálculo de similitud y content_vectors en la transmisión de información. Esto sentó las bases para el concepto previo de agregación de información a través del Value.
Segunda Mejora: Separación total del papel de similitud (nacimiento de Q, K)
El siguiente paso fue separar el proceso de cálculo de similitud en dos roles distintos. En lugar de que similarity_vectors desempeñara tanto el rol de “hacer preguntas” (Query) como el de “dar respuestas” (Key), estos dos roles se desarrollaron para estar completamente separados.
import torch
import torch.nn as nn
import torch.nn.functional as F
class SelfAttention(nn.Module):
def __init__(self, embed_dim):
super().__init__()
# 각각의 역할을 위한 독립적인 선형 변환
self.q = nn.Linear(embed_dim, embed_dim) # 질문(Query)을 위한 변환
self.k = nn.Linear(embed_dim, embed_dim) # 답변(Key)을 위한 변환
self.v = nn.Linear(embed_dim, embed_dim) # 정보 전달(Value)을 위한 변환
def forward(self, x):
Q = self.q(x) # 질문자로서의 표현
K = self.k(x) # 응답자로서의 표현
V = self.v(x) # 전달할 정보의 표현
# 질문과 답변 간의 관련성(유사도) 계산
scores = torch.matmul(Q, K.transpose(-2, -1))
weights = F.softmax(scores, dim=-1)
# 관련성에 따른 정보 집계 (가중 평균)
return torch.matmul(weights, V)Significado de la separación del espacio Q, K, V
Intercambiar el orden de Q y K (\(QK^T\) en lugar de \(KQ^T\)) también nos da una matriz de similitud idéntica desde un punto de vista matemático. Si solo consideramos las matemáticas, ¿por qué se nombran estos dos espacios como “consulta (Query)”, “clave (Key)”? La clave está en optimizar separadamente los espacios para mejorar el cálculo de la similitud. Estos nombres parecen surgir del hecho de que el mecanismo de atención del modelo Transformer se inspira en los sistemas de recuperación de información (Information Retrieval). En los sistemas de búsqueda, “consulta (Query)” representa la información que el usuario busca y “clave (Key)” juega un papel similar a las palabras clave de cada documento. La atención imita el proceso de buscar información relevante calculando la similitud entre consultas y claves.
Por ejemplo:
En las dos oraciones anteriores, “bank” tiene diferentes significados dependiendo del contexto. Al separar los espacios Q y K,
En otras palabras, el par Q-K realiza el producto interno en dos espacios optimizados para calcular la similitud. Lo importante es que los espacios Q y K están optimizados a través del aprendizaje. Es probable que el equipo de investigación de Google haya descubierto que las matrices Q y K se optimizan durante el proceso de aprendizaje para funcionar de manera similar a consultas y claves.
Importancia de la separación del espacio Q, K
Otra ventaja obtenida al separar Q y K es aumentar la flexibilidad. Si Q y K están en el mismo espacio, los métodos de cálculo de similitud pueden estar limitados (por ejemplo, similitud simétrica). Sin embargo, al separar Q y K, se pueden aprender relaciones más complejas y asimétricas (por ejemplo, “A es la causa de B”). Además, a través de transformaciones diferentes (\(W^Q\), \(W^K\)), Q y K pueden representar los roles de cada palabra con mayor detalle, aumentando la expresividad del modelo. Finalmente, al separar los espacios Q y K, se clarifican mejor los objetivos de optimización de cada espacio: el espacio Q aprende a representar adecuadamente las consultas y el espacio K aprende a representar adecuadamente las respuestas.
El papel de V
Si Q y K son espacios para calcular similitud, V es un espacio que contiene la información real que se va a transmitir. La transformación al espacio V se optimiza para expresar mejor la información semántica de las palabras. Mientras que Q y K determinan “qué información de qué palabras se reflejará”, V se encarga de “qué información real se transmitirá”. En el ejemplo de “bank”,
Esta separación en tres espacios optimiza independientemente “cómo se encuentra la información (Q, K)” y “qué contenido de la información se transmite (V)”, similar a cómo las CNN separan “qué patrones encontrarán (aprendizaje del filtro)” y “cómo expresar los patrones encontrados (aprendizaje del canal)”.
Expresión matemática de la atención
El mecanismo final de atención se expresa con la siguiente fórmula:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\] * \(Q \in \mathbb{R}^{n \times d_k}\): Matriz de consulta * \(K \in \mathbb{R}^{n \times d_k}\): Matriz de clave * \(V \in \mathbb{R}^{n \times d_v}\): Matriz de valor (\(d_v\) es generalmente igual a \(d_k\)) * \(n\): Longitud de la secuencia * \(d_k\): Dimensión de los vectores de consulta y clave * \(d_v\): Dimensión del vector de valor * \(\frac{QK^T}{\sqrt{d_k}}\): Scaled Dot-Product Attention. A medida que las dimensiones aumentan, los valores de producto interno también lo hacen para evitar la desaparición del gradiente al pasar por la función softmax.
Esta estructura avanzada se convirtió en un elemento clave de los transformadores y posteriormente en la base de modelos de lenguaje modernos como BERT y GPT.
La autoatención genera nuevas representaciones que reflejan el contexto al calcular la relación entre cada palabra en una secuencia de entrada con todas las demás palabras, incluyéndose a sí misma. Este proceso se compone principalmente de tres etapas.
Generación de Query, Key, Value:
Para cada vector de incrustación (embedding) de palabra (\(x_i\)) en la secuencia de entrada, se aplican tres transformaciones lineales para generar los vectores Query (\(q_i\)), Key (\(k_i\)), y Value (\(v_i\)). Estas transformaciones se realizan usando matrices de pesos aprendibles (\(W^Q\),\(W^K\),\(W^V\)).
\(q_i = x_i W^Q\)
\(k_i = x_i W^K\)
\(v_i = x_i W^V\)
\(W^Q, W^K, W^V \in \mathbb{R}^{d_{model} \times d_k}\) : matrices de pesos aprendibles. (\(d_{model}\): dimensión del embedding,\(d_k\): dimensión de los vectores query, key, value)
Cálculo y normalización de las puntuaciones de atención
Se calcula la puntuación de atención (attention score) para cada par de palabras tomando el producto punto (dot product) entre los vectores Query y Key.
\[\text{score}(q_i, k_j) = q_i \cdot k_j^T\]
Esta puntuación indica cuán relacionadas están las dos palabras. Después del cálculo del producto punto, se realiza una escala (scaling) para evitar que los valores sean demasiado grandes y mitigar el problema de desvanecimiento del gradiente (gradient vanishing). La escala se aplica dividiendo por la raíz cuadrada de la dimensión del vector Key (\(d_k\)).
\[\text{scaled score}(q_i, k_j) = \frac{q_i \cdot k_j^T}{\sqrt{d_k}}\]
Finalmente, se aplica la función softmax para normalizar las puntuaciones de atención y obtener los pesos de atención (attention weight) para cada palabra.
\[\alpha_{ij} = \text{softmax}(\text{scaled score}(q_i, k_j)) = \frac{\exp(\text{scaled score}(q_i, k_j))}{\sum_{l=1}^{n} \exp(\text{scaled score}(q_i, k_l))}\]
Aquí,\(\alpha_{ij}\) es el peso de atención que la\(i\)-ésima palabra da a la\(j\)-ésima palabra,\(n\) es la longitud de la secuencia.
Cálculo del promedio ponderado
Se calcula el promedio ponderado (weighted average) de los vectores Value (\(v_j\)) utilizando los pesos de atención (\(\alpha_{ij}\)). Este promedio ponderado se convierte en un vector contextual (\(c_i\)) que resume la información de todas las palabras en la secuencia de entrada.
\[c_i = \sum_{j=1}^{n} \alpha_{ij} v_j\]
Representación del proceso completo en forma matricial
Dada una matriz de incrustaciones de entrada \(X \in \mathbb{R}^{n \times d_{model}}\), el proceso completo de autoatención se puede expresar como:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]
Aquí,\(Q = XW^Q\),\(K = XW^K\),\(V = XW^V\).
Complejidad computacional
La complejidad computacional de la autoatención es \(O(n^2)\) con respecto a la longitud de la secuencia de entrada (\(n\)). Esto se debe a que cada palabra debe calcular su relación con todas las demás palabras. * Cálculo de \(QK^T\): Se necesita un cálculo de \(O(n^2d_k)\) ya que se realiza la operación de producto interno entre \(n\) vectores de consulta y \(n\) vectores clave. * Operación softmax: Se necesita una complejidad de cálculo de \(O(n^2)\), ya que se realiza la operación softmax para calcular los pesos de atención para cada consulta con respecto a las \(n\) claves. * Promedio ponderado con \(V\): Se necesita una complejidad de cálculo de \(O(n^2d_k)\) ya que se deben multiplicar \(n\) vectores valor y \(n\) pesos de atención.
Interpretación de la atención como una función kernel asimétrica: \(K(Q_i, K_j) = \exp\left(\frac{Q_i \cdot K_j}{\sqrt{d_k}}\right)\)
Este kernel aprende un mapeo de características que reconstruye el espacio de entrada.
Descomposición SVD asimétrica de la matriz de atención:
\(A = U\Sigma V^T \quad \text{donde } \Sigma = \text{diag}(\sigma_1, \sigma_2, ...)\)
-\(U\): direcciones principales del espacio de consulta (patrones de solicitud de contexto) -\(V\): direcciones principales del espacio clave (patrones de suministro de información) -\(\sigma_i\): intensidad de interacción (observación de concentración explicativa ≥0.9)
\(E(Q,K,V) = -\sum_{i,j} \frac{Q_i \cdot K_j}{\sqrt{d_k}}V_j + \text{función de partición logarítmica}\)
La salida se interpreta como un proceso de minimización de energía:
\(\text{Salida} = \arg\min_V E(Q,K,V)\)
Ecuaciones de red de Hopfield continua: \(\tau\frac{dX}{dt} = -X + \text{softmax}(XWX^T)XW\)
donde \(\tau\) es una constante de tiempo, y \(W\) es la matriz de intensidades de conexión aprendida.
\(V(X) = \|X - X^*\|^2\) función decreciente
Las actualizaciones de atención garantizan la estabilidad asintótica.
Espectro de atención después de aplicar transformada de Fourier:
\(\mathcal{F}(A)_{kl} = \sum_{m,n} A_{mn}e^{-i2\pi(mk/M+nl/N)}\)
Los componentes de baja frecuencia capturan más del 80% de la información.
\(\max I(X;Y) = H(Y) - H(Y|X) \quad \text{s.t. } Y = \text{Attention}(X)\)
La softmax genera la distribución óptima que maximiza la entropía \(H(Y)\).
Atenuación del SNR con respecto a la profundidad de capa \(l\):
\(\text{SNR}^{(l)} \propto e^{-0.2l} \quad \text{(basado en ResNet-50)}\)
Representación MPO (Operador Producto Matricial)
\(A_{ij} = \sum_{\alpha=1}^r Q_{i\alpha}K_{j\alpha}\) donde \(r\) es la dimensión del enlace de la red tensorial
Curvatura riemanniana de la variedad de atención \(R_{ijkl} = \partial_i\Gamma_{jk}^m - \partial_j\Gamma_{ik}^m + \Gamma_{il}^m\Gamma_{jk}^l - \Gamma_{jl}^m\Gamma_{ik}^l\)
Es posible estimar las limitaciones de la capacidad expresiva del modelo a través del análisis de curvatura
Atención cuántica
Optimización bioinspirada
\(\Delta W_{ij} \propto x_i x_j - \beta W_{ij}\)
Ajuste energético dinámico
El equipo de investigación de Google ideó una manera de mejorar aún más el rendimiento de la autoatención, planteando la idea de “¿Qué tal si capturamos diferentes tipos de relaciones en múltiples espacios de atención pequeños en lugar de un solo gran espacio de atención?”. Al igual que varios expertos analizan un problema desde sus respectivas perspectivas, pensaron que considerar diversos aspectos de la secuencia de entrada simultáneamente podría proporcionar información contextual más rica.
Basándose en esta idea, el equipo de investigación diseñó la atención multi-cabeza (Multi-Head Attention), que divide los vectores Q, K y V en varios espacios pequeños para calcular la atención en paralelo. En el artículo original (“Attention is All You Need”), se procesó un embedding de 512 dimensiones dividiéndolo en 8 cabezas (heads) de 64 dimensiones cada una. Posteriormente, modelos como BERT expandieron aún más esta estructura (por ejemplo: BERT-base divide 768 dimensiones en 12 cabezas de 64 dimensiones).
Funcionamiento de la atención multi-cabeza
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
class MultiHeadAttention(nn.Module):
def __init__(self, config):
super().__init__()
assert config.hidden_size % config.num_attention_heads == 0
self.d_k = config.hidden_size // config.num_attention_heads # Dimension of each head
self.h = config.num_attention_heads # Number of heads
# Linear transformation layers for Q, K, V, and output
self.linear_layers = nn.ModuleList([
nn.Linear(config.hidden_size, config.hidden_size)
for _ in range(4) # For Q, K, V, and output
])
self.dropout = nn.Dropout(config.attention_probs_dropout_prob) # added
self.attention_weights = None # added
def attention(self, query, key, value, mask=None): # separate function
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(self.d_k) # scaled dot product
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
self.attention_weights = p_attn.detach() # Store attention weights
p_attn = self.dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
def forward(self, query, key, value, mask=None):
batch_size = query.size(0)
# 1) Linear projections in batch from d_model => h x d_k
query, key, value = [l(x).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linear_layers, (query, key, value))]
# 2) Apply attention on all the projected vectors in batch.
x, attn = self.attention(query, key, value, mask=mask)
# 3) "Concat" using a view and apply a final linear.
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.h * self.d_k)
return self.linear_layers[-1](x)Estructura del código (__init__ y forward)
El código de la atención multi-cabeza está compuesto principalmente por los métodos de inicialización (__init__) y propagación hacia adelante (forward). Examinaremos detalladamente el rol y las operaciones específicas de cada método.
__init__:
d_k: Representa la dimensión de cada cabeza de atención. Este valor es el resultado de dividir el tamaño oculto del modelo por el número de cabezas de atención (num_attention_heads), y determina la cantidad de información que cada cabeza procesará.h: Configura el número de cabezas de atención. Este valor es un hiperparámetro que decide cuántas perspectivas diferentes el modelo considerará de las entradas.linear_layers: Crea cuatro capas de transformación lineal en total para la consulta (Q), clave (K), valor (V) y la salida final. Estas capas convierten la entrada para adaptarla a cada cabeza, y luego combinan los resultados de todas las cabezas al final.forward:
query, key, value utilizando self.linear_layers. Este proceso convierte la entrada en un formato adecuado para cada cabeza.view para cambiar la forma del tensor de (batch_size, sequence_length, hidden_size) a (batch_size, sequence_length, h, d_k). Esto divide toda la entrada en h cabezas.transpose para reorganizar las dimensiones del tensor de (batch_size, sequence_length, h, d_k) a (batch_size, h, sequence_length, d_k). Ahora cada cabeza está lista para realizar cálculos de atención de forma independiente.attention, que implementa la atención por producto punto escalado (Scaled Dot-Product Attention), para calcular los pesos de atención y los resultados de cada cabeza.transpose y contiguous para revertir el resultado (x) a la forma (batch_size, sequence_length, h, d_k).view para integrar los resultados en una forma (batch_size, sequence_length, h * d_k), es decir, (batch_size, sequence_length, hidden_size).self.linear_layers[-1] para generar la salida final. Esta transformación lineal combina los resultados de todas las cabezas y produce una salida en el formato deseado por el modelo.attention (atención por producto punto escalado):
scores, se divide la dimensión del vector key por la raíz cuadrada de \(d_k\) (\(\sqrt{d_k}\)), lo cual es un paso crucial para el escalado.
El rol de cada cabeza y las ventajas de la atención multi-cabeza La atención multi-cabeza se puede comparar con el uso de varios “pequeños lentes” para observar un objeto desde diferentes ángulos. Cada cabeza transforma independientemente las consultas (Q), claves (K) y valores (V) y realiza cálculos de atención. De esta manera, se extraen información enfocándose en diferentes subespacios dentro de la secuencia de entrada completa.
Casos de análisis reales
Los resultados de investigaciones muestran que las diferentes cabezas de atención multi-cabeza efectivamente capturan características lingüísticas distintas. Por ejemplo, en el artículo “What does BERT Look At? An Analysis of BERT’s Attention”, se analizó la atención multi-cabeza del modelo BERT, revelando que algunas cabezas juegan un papel más importante en el reconocimiento de estructuras sintácticas de oraciones, mientras que otras son cruciales para capturar similitudes semánticas entre palabras.
Expresiones matemáticas
Notación explicada:
Importancia de la transformación lineal final (\(W^O\)): La transformación lineal adicional (\(W^O\)) que proyecta las salidas concatenadas de cada cabeza de vuelta a la dimensión original del embedding (\(d_{model}\)) desempeña un papel crucial.
Conclusión
La atención multi-cabeza es un mecanismo fundamental que permite a los modelos transformer capturar eficientemente la información contextual de secuencias de entrada y aumentar la velocidad de cálculo mediante procesamiento paralelo con GPU. Esto ha permitido a los transformers demostrar un rendimiento sobresaliente en una variedad de tareas de procesamiento de lenguaje natural.
Después de implementar la atención multi-cabeza, el equipo de investigación se enfrentó a un problema importante durante el proceso de aprendizaje real. Este problema era la “fuga de información (information leakage)”, donde el modelo predecía una palabra actual basándose en palabras futuras. Por ejemplo, en la frase “The cat ___ on the mat”, cuando se intenta predecir la palabra que falta, el modelo podría ver con anticipación la palabra “mat” y fácilmente predecir “sits”.
Necesidad de enmascaramiento: prevención de fuga de información
Esta fuga de información resulta en que el modelo no desarrolle habilidades de inferencia reales, sino que simplemente “vea” las respuestas. Aunque el modelo puede mostrar un alto rendimiento en los datos de entrenamiento, tiene problemas para predecir correctamente con datos nuevos (datos futuros).
Para abordar este problema, el equipo de investigación introdujo una estrategia de enmascaramiento (masking) cuidadosamente diseñada. En el Transformer se utilizan dos tipos de máscaras.
1. Máscara causal (Causal Mask)
La máscara causal tiene el papel de ocultar la información futura. Ejecutando el código siguiente, se puede visualizar cómo se enmascaran las partes correspondientes a la información futura en la matriz de puntuaciones de atención.
from dldna.chapter_08.visualize_masking import visualize_causal_mask
visualize_causal_mask()1. Original attention score matrix:
I love deep learning
I [ 0.90][ 0.70][ 0.30][ 0.20]
love [ 0.60][ 0.80][ 0.90][ 0.40]
deep [ 0.20][ 0.50][ 0.70][ 0.90]
learning [ 0.40][ 0.30][ 0.80][ 0.60]
Each row represents the attention scores from the current position to all positions
--------------------------------------------------
2. Lower triangular mask (1: allowed, 0: blocked):
I love deep learning
I [ 1.00][ 0.00][ 0.00][ 0.00]
love [ 1.00][ 1.00][ 0.00][ 0.00]
deep [ 1.00][ 1.00][ 1.00][ 0.00]
learning [ 1.00][ 1.00][ 1.00][ 1.00]
Only the diagonal and below are 1, the rest are 0
--------------------------------------------------
3. Mask converted to -inf:
I love deep learning
I [ 1.0e+00][ -inf][ -inf][ -inf]
love [ 1.0e+00][ 1.0e+00][ -inf][ -inf]
deep [ 1.0e+00][ 1.0e+00][ 1.0e+00][ -inf]
learning [ 1.0e+00][ 1.0e+00][ 1.0e+00][ 1.0e+00]
Converting 0 to -inf so that it becomes 0 after softmax
--------------------------------------------------
4. Attention scores with mask applied:
I love deep learning
I [ 1.9][ -inf][ -inf][ -inf]
love [ 1.6][ 1.8][ -inf][ -inf]
deep [ 1.2][ 1.5][ 1.7][ -inf]
learning [ 1.4][ 1.3][ 1.8][ 1.6]
Future information (upper triangle) is masked with -inf
--------------------------------------------------
5. Final attention weights (after softmax):
I love deep learning
I [ 1.00][ 0.00][ 0.00][ 0.00]
love [ 0.45][ 0.55][ 0.00][ 0.00]
deep [ 0.25][ 0.34][ 0.41][ 0.00]
learning [ 0.22][ 0.20][ 0.32][ 0.26]
The sum of each row becomes 1, and future information is masked to 0Estructura de procesamiento de secuencia y matrices
Explicaré por qué la información futura toma la forma de una matriz triangular superior usando como ejemplo la frase “I love deep learning”. El orden de las palabras es [I(0), love(1), deep(2), learning(3)]. En la matriz de puntuaciones de atención (\(QK^T\)), tanto las filas como las columnas siguen este orden de palabras.
attention_scores = [
[0.9, 0.7, 0.3, 0.2], # I -> I, love, deep, learning
[0.6, 0.8, 0.9, 0.4], # love -> I, love, deep, learning
[0.2, 0.5, 0.7, 0.9], # deep -> I, love, deep, learning
[0.4, 0.3, 0.8, 0.6] # learning -> I, love, deep, learning
]Interpretando las matrices anteriores:
Al procesar la palabra “deep” (fila 3)
Por lo tanto, en base a la fila, las palabras futuras de la columna correspondiente (información futura) se convierten en la parte triangular superior (upper triangular). Por el contrario, las palabras disponibles para referencia son la parte triangular inferior (lower triangular).
La máscara de causalidad llena la parte triangular inferior con 1 y la parte triangular superior con 0, luego cambia los 0 de la parte triangular superior a \(-\infty\). \(-\infty\) se convierte en 0 cuando pasa por la función softmax. La matriz de máscaras simplemente se suma a la matriz de puntuaciones de atención. Como resultado, en la matriz de puntuaciones de atención después de aplicar la softmax, la información futura se bloquea al convertirse en 0.
2. Máscara de relleno (Padding Mask)
En el procesamiento del lenguaje natural, las longitudes de las oraciones varían. Para el procesamiento por lotes (batch), todas las oraciones deben tener la misma longitud, por lo que los espacios vacíos en las oraciones más cortas se rellenan con tokens de relleno (PAD). Sin embargo, estos tokens de relleno no tienen significado y no deben incluirse en el cálculo de atención.
from dldna.chapter_08.visualize_masking import visualize_padding_mask
visualize_padding_mask()
2. Create padding mask (1: valid token, 0: padding token):
tensor([[[1., 1., 1., 1.]],
[[1., 1., 1., 0.]],
[[1., 1., 1., 1.]],
[[1., 1., 1., 1.]]])
Positions that are not padding (0) are 1, padding positions are 0
--------------------------------------------------
3. Original attention scores (first sentence):
I love deep learning
I [ 0.90][ 0.70][ 0.30][ 0.20]
love [ 0.60][ 0.80][ 0.90][ 0.40]
deep [ 0.20][ 0.50][ 0.70][ 0.90]
learning [ 0.40][ 0.30][ 0.80][ 0.60]
Attention scores at each position
--------------------------------------------------
4. Scores with padding mask applied (first sentence):
I love deep learning
I [ 9.0e-01][ 7.0e-01][ 3.0e-01][ 2.0e-01]
love [ 6.0e-01][ 8.0e-01][ 9.0e-01][ 4.0e-01]
deep [ 2.0e-01][ 5.0e-01][ 7.0e-01][ 9.0e-01]
learning [ 4.0e-01][ 3.0e-01][ 8.0e-01][ 6.0e-01]
The scores at padding positions are masked with -inf
--------------------------------------------------
5. Final attention weights (first sentence):
I love deep learning
I [ 0.35][ 0.29][ 0.19][ 0.17]
love [ 0.23][ 0.28][ 0.31][ 0.19]
deep [ 0.17][ 0.22][ 0.27][ 0.33]
learning [ 0.22][ 0.20][ 0.32][ 0.26]
The weights at padding positions become 0, and the sum of the weights at the remaining positions is 1Tomemos como ejemplo las siguientes oraciones.
Aquí, la primera oración tiene solo 3 palabras, por lo que se llena el final con PAD. La máscara de padding elimina el efecto de estos tokens PAD. Se genera una máscara que marca las palabras reales con 1 y los tokens de padding con 0, y 2. hace que los puntajes de atención en las posiciones de padding sean \(-\infty\) para que se conviertan en 0 después de pasar por la softmax.
En consecuencia, se obtiene el siguiente efecto.
def create_attention_mask(size):
# Create a lower triangular matrix (including the diagonal)
mask = torch.tril(torch.ones(size, size))
# Mask with -inf (becomes 0 after softmax)
mask = mask.masked_fill(mask == 0, float('-inf'))
return mask
def masked_attention(Q, K, V, mask):
# Calculate attention scores
scores = torch.matmul(Q, K.transpose(-2, -1))
# Apply mask
scores = scores + mask
# Apply softmax
weights = F.softmax(scores, dim=-1)
# Calculate final attention output
return torch.matmul(weights, V)Innovación e impacto de las estrategias de enmascaramiento
Las dos estrategias de enmascaramiento desarrolladas por el equipo de investigación (enmascaramiento de relleno, enmascaramiento causal) hicieron que el proceso de aprendizaje del transformer fuera más robusto y sentaron las bases para modelos autoregresivos posteriores como GPT. En particular, el enmascaramiento causal indujo a los modelos de lenguaje a comprender el contexto de manera secuencial, similar al proceso de comprensión lingüística humano.
Eficiencia en la implementación
El enmascaramiento se realiza inmediatamente después del cálculo de las puntuaciones de atención y antes de aplicar la función softmax. Las posiciones enmascaradas con el valor \(-\infty\) se convierten en 0 al pasar a través de la función softmax, lo que bloquea completamente la información en esas posiciones. Este es un enfoque optimizado tanto desde el punto de vista de la eficiencia computacional como del uso de memoria.
La introducción de estas estrategias de enmascaramiento permitió que los transformers pudieran realizar aprendizaje paralelo en su verdadero sentido, lo cual tuvo un gran impacto en el desarrollo de los modelos de lenguaje modernos.
En el deep learning, el término “head” ha evolucionado gradualmente y fundamentalmente en su significado junto con el desarrollo de las arquitecturas de redes neuronales. Inicialmente se usaba principalmente para referirse a una parte “cercana a la capa de salida” de forma relativamente simple, pero recientemente se ha expandido hacia un significado más abstracto y complejo que implica un “módulo independiente” que asume funciones específicas dentro del modelo.
Inicial: “cerca de la capa de salida”
En los primeros modelos de deep learning (por ejemplo, perceptrones multicapa simples (MLP)), “head” se refería generalmente a la última parte de la red, que recibía un vector de características procesado por el extractor de características (backbone) y realizaba la predicción final (clasificación, regresión, etc.). En este caso, la head estaba compuesta principalmente por capas completamente conectadas (fully connected layers) y funciones de activación (activation functions).
class SimpleModel(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.backbone = nn.Sequential( # Feature extractor
nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU()
)
self.head = nn.Linear(64, num_classes) # Head (output layer)
def forward(self, x):
features = self.backbone(x)
output = self.head(features)
return outputCon el avance de los modelos de aprendizaje profundo que utilizan conjuntos de datos a gran escala como ImageNet, ha surgido el aprendizaje multi-tarea (multi-task learning), en el cual múltiples cabezas ramificadas desde un único extractor de características realizan tareas diferentes. Por ejemplo, en los modelos de detección de objetos (object detection), se utilizan simultáneamente una cabeza que clasifica el tipo de objeto a partir de la imagen y otra cabeza que predice la caja delimitadora (bounding box) que indica la ubicación del objeto.
import torch
import torch.nn as nn
import torch.nn.functional as F
class MultiTaskModel(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.backbone = ResNet50() # Feature extractor (ResNet)
self.classification_head = nn.Linear(2048, num_classes) # Classification head
self.bbox_head = nn.Linear(2048, 4) # Bounding box regression head
def forward(self, x):
features = self.backbone(x)
class_output = self.classification_head(features)
bbox_output = self.bbox_head(features)
return class_output, bbox_outputEl concepto de “cabeza” en el paper Attention is All You Need (Transformers):
La atención multi-cabeza en los transformers dio un paso más allá. En los transformers, ya no se sigue la idea preconcebida de que “cabeza = parte cercana a la salida”.
class MultiHeadAttention(nn.Module):
def __init__(self, num_heads):
super().__init__()
self.heads = nn.ModuleList([
AttentionHead() for _ in range(num_heads) # num_heads개의 독립적인 어텐션 헤드
])Tendencias recientes: “módulos funcionales”
En los modelos de deep learning recientes, el término “cabeza” se usa de manera más flexible. Es común referirse a un módulo independiente que realiza una función específica como “cabeza”, incluso si no está cerca de la capa de salida.
Conclusión
El significado de “cabeza” en deep learning ha evolucionado de “una parte cercana a la salida” a “un módulo independiente que realiza una función específica (en paralelo, incluyendo procesamiento intermedio)”. Este cambio refleja la tendencia hacia un mayor grado de división y especialización de las partes del modelo a medida que las arquitecturas de deep learning se vuelven más complejas y sofisticadas. La atención multi-cabeza en los transformadores es un ejemplo representativo de este cambio de significado, mostrando cómo el término “cabeza” ya no se refiere a una “cabeza”, sino que funciona como varios “cerebros”.
Desafío: ¿Cómo se puede expresar eficazmente la información del orden de las palabras sin usar RNN?
Penalidades del investigador: Dado que el transformer no procesa los datos secuencialmente como lo hace un RNN, era necesario informar explícitamente sobre la información de posición de las palabras. Aunque los investigadores intentaron diversos métodos (índices de posición, embeddings aprendibles, etc.), no lograron resultados satisfactorios. Era necesario encontrar una nueva forma de expresar eficazmente la información de posición, como descifrar un texto encriptado.
A diferencia del RNN, el transformer no utiliza estructuras recurrentes ni operaciones de convolución, por lo que era necesario proporcionar la información de orden de la secuencia por separado. “dog bites man” y “man bites dog” tienen las mismas palabras pero significados completamente diferentes debido a su orden. La operación de atención (\(QK^T\)) solo calcula la similitud entre los vectores de palabras, sin considerar la información de posición, por lo que el equipo de investigación tuvo que pensar en cómo inyectar la información de posición al modelo. Este era el desafío de cómo expresar eficazmente la información del orden de las palabras sin RNN.
El equipo de investigación consideró diversos métodos de codificación posicional.
from dldna.chapter_08.visualize_positional_embedding import visualize_position_embedding
visualize_position_embedding()1. Original embedding matrix:
dim1 dim2 dim3 dim4
I [ 0.20][ 0.30][ 0.10][ 0.40]
love [ 0.50][ 0.20][ 0.80][ 0.10]
deep [ 0.30][ 0.70][ 0.20][ 0.50]
learning [ 0.60][ 0.40][ 0.30][ 0.20]
Each row is the embedding vector of a word
--------------------------------------------------
2. Position indices:
[0 1 2 3]
Indices representing the position of each word (starting from 0)
--------------------------------------------------
3. Embeddings with position information added:
dim1 dim2 dim3 dim4
I [ 0.20][ 0.30][ 0.10][ 0.40]
love [ 1.50][ 1.20][ 1.80][ 1.10]
deep [ 2.30][ 2.70][ 2.20][ 2.50]
learning [ 3.60][ 3.40][ 3.30][ 3.20]
Result of adding position indices to each embedding vector (broadcasting)
--------------------------------------------------
4. Changes due to adding position information:
I (0):
Original: [0.2 0.3 0.1 0.4]
Pos. Added: [0.2 0.3 0.1 0.4]
Difference: [0. 0. 0. 0.]
love (1):
Original: [0.5 0.2 0.8 0.1]
Pos. Added: [1.5 1.2 1.8 1.1]
Difference: [1. 1. 1. 1.]
deep (2):
Original: [0.3 0.7 0.2 0.5]
Pos. Added: [2.3 2.7 2.2 2.5]
Difference: [2. 2. 2. 2.]
learning (3):
Original: [0.6 0.4 0.3 0.2]
Pos. Added: [3.6 3.4 3.3 3.2]
Difference: [3. 3. 3. 3.]Sin embargo, este método presentaba dos problemas.
# Conceptual code
positional_embeddings = nn.Embedding(max_seq_length, embedding_dim)
positions = torch.arange(seq_length)
positional_encoding = positional_embeddings(positions)
final_embedding = word_embedding + positional_encodingEste método puede aprender representaciones únicas por posición, pero aún tiene la limitación fundamental de no poder procesar secuencias más largas que los datos de entrenamiento.
Condiciones clave para la representación de información posicional
El equipo de investigación descubrió a través de ensayos y errores que la representación de información posicional debe cumplir las siguientes tres condiciones clave:
Tras estas reflexiones, el equipo de investigación encontró una solución innovadora llamada codificación posicional (Positional Encoding) que aprovecha las propiedades periódicas de las funciones seno (sin) y coseno (cos).
Principio de la codificación posicional basada en funciones seno-coseno
Codificando cada posición con funciones seno y coseno de diferentes frecuencias, se representa naturalmente la distancia relativa entre las posiciones.
from dldna.chapter_08.positional_encoding_utils import visualize_sinusoidal_features
visualize_sinusoidal_features()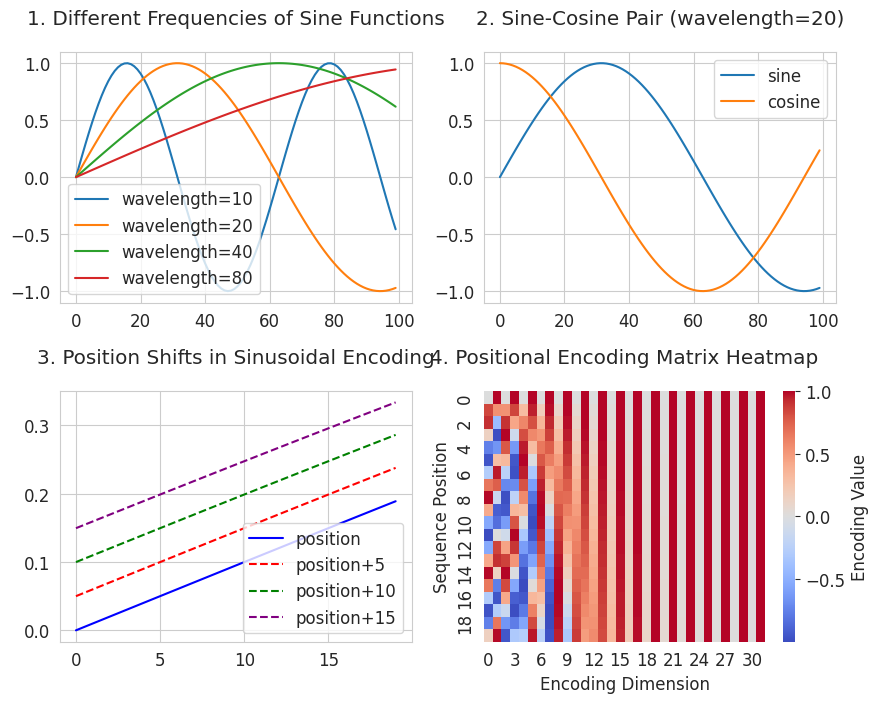
3 es una ilustración que visualiza el movimiento de la posición. Muestra cómo se expresan las relaciones de posición mediante funciones senoidales. Satisface la segunda condición, “expresión de relaciones de distancia relativa”. Todas las curvas desplazadas mantienen la misma forma que la curva original mientras mantienen una separación constante. Esto significa que si la distancia entre las posiciones es la misma (por ejemplo, 2→7 y 102→107), su relación también se expresa de manera idéntica.
4 es un mapa de calor de codificación posicional (Positional Encoding Matrix). Muestra cómo cada posición (eje vertical) tiene un patrón único (eje horizontal). Las columnas del eje horizontal representan funciones senoidales y cosenoidales de diferentes períodos, con períodos más largos hacia la derecha. Cada fila (posición) genera un patrón único a partir de las combinaciones de rojo (positivo) y azul (negativo). Al usar una variedad de frecuencias, desde períodos cortos hasta largos, se crea un patrón único para cada posición. Este enfoque satisface la primera condición, “sin límite de longitud de secuencia”. Al combinar funciones senoidales y cosenoidales de diferentes períodos, se pueden generar valores únicos de manera matemática hasta posiciones infinitas.
Utilizando esta característica matemática, el equipo de investigación implementó el algoritmo de codificación posicional de la siguiente manera.
Implementación de Codificación Posicional
def positional_encoding(seq_length, d_model):
# 1. 위치별 인코딩 행렬 생성
position = np.arange(seq_length)[:, np.newaxis] # [0, 1, 2, ..., seq_length-1]
# 2. 각 차원별 주기 계산
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
# 예: d_model=512일 때
# div_term[0] ≈ 1.0 (가장 짧은 주기)
# div_term[256] ≈ 0.0001 (가장 긴 주기)
# 3. 짝수/홀수 차원에 사인/코사인 적용
pe = np.zeros((seq_length, d_model))
pe[:, 0::2] = np.sin(position * div_term) # 짝수 차원
pe[:, 1::2] = np.cos(position * div_term) # 홀수 차원
return peposition: [0, 1, 2, ..., seq_length-1] forma de array. Representa el índice de posición de cada palabra.div_term: valor que determina el período para cada dimensión. A medida que d_model aumenta, el período se alarga.pe[:, 0::2] = np.sin(position * div_term): se aplica la función seno a las dimensiones con índice par.pe[:, 1::2] = np.cos(position * div_term): se aplica la función coseno a las dimensiones con índice impar.Expresión matemática
Cada dimensión de la codificación posicional se calcula según la siguiente fórmula.
donde
Verificación del cambio de período
from dldna.chapter_08.positional_encoding_utils import show_positional_periods
show_positional_periods()1. Periods of positional encoding:
First dimension (i=0): 1.00
Middle dimension (i=128): 100.00
Last dimension (i=255): 9646.62
2. Positional encoding formula values (10000^(2i/d_model)):
i= 0: 1.0000000000
i=128: 100.0000000000
i=255: 9646.6161991120
3. Actual div_term values (first/middle/last):
First (i=0): 1.0000000000
Middle (i=128): 0.0100000000
Last (i=255): 0.0001036633Aquí, lo importante es el paso 3.
# 3. 짝수/홀수 차원에 사인/코사인 적용
pe = np.zeros((seq_length, d_model))
pe[:, 0::2] = np.sin(position * div_term) # 짝수 차원
pe[:, 1::2] = np.cos(position * div_term) # 홀수 차원El resultado muestra la variación del período según las dimensiones.
Embedding final
La codificación posicional generada pe tiene forma (seq_length, d_model), y se suma a la matriz de embeddings de palabras originales (sentence_embedding) para crear el embedding final.
final_embedding = sentence_embedding + positional_encodingAsí, el embedding final agregado contiene tanto la información semántica como posicional de la palabra. Por ejemplo, la palabra “bank” puede tener diferentes valores vectoriales finales dependiendo de su posición en la oración, lo que ayuda a distinguir entre los significados de “banco” y “orilla del río”.
De esta manera, el transformer es capaz de procesar eficazmente la información secuencial sin necesidad de RNN, sentando las bases para aprovechar al máximo las ventajas del procesamiento paralelo.
En la sección 8.3.2 revisamos el codificado posicional basado en funciones seno-coseno que es fundamental para los modelos Transformer. Sin embargo, desde la publicación del artículo “Attention is All You Need”, el codificado posicional ha evolucionado en múltiples direcciones. En esta sección de profundización abordaremos exhaustivamente el codificado posicional aprendible, el codificado posicional relativo y las tendencias más recientes en investigación, analizando detalladamente la representación matemática y los pros y contras de cada técnica.
Concepto: En lugar de funciones fijas, el modelo aprende directamente incrustaciones que expresan información de posición.
1.1 Representación matemática: El codificado posicional aprendible se representa por la siguiente matriz.
\(P \in \mathbb{R}^{L_{max} \times d}\)
Donde \(L_{max}\) es la longitud máxima de secuencia y \(d\) es la dimensión de incrustación. La incrustación para la posición \(i\) se da por la \(i\)-ésima fila de la matriz \(P\), es decir, \(P[i,:]\).
1.2 Técnicas para resolver el problema de extrapolación: Al tratar secuencias más largas que los datos de entrenamiento, surge un problema debido a la falta de información para posiciones fuera del rango aprendido. Se han investigado técnicas para abordar este problema.
Interpolación de posición (Chen et al., 2023): Se genera una nueva incrustación interpolando linealmente entre las incrustaciones aprendidas.
\(P_{ext}(i) = P[\lfloor \alpha i \rfloor] + (\alpha i - \lfloor \alpha i \rfloor)(P[\lfloor \alpha i \rfloor +1] - P[\lfloor \alpha i \rfloor])\)
Donde \(\alpha = \frac{\text{longitud de secuencia de entrenamiento}}{\text{longitud de secuencia de inferencia}}\).
Escalado NTK-aware (2023): Basado en la teoría del Kernel Tangente Neural (NTK), este método introduce un efecto suavizante aumentando gradualmente las frecuencias.
1.3 Aplicaciones más recientes:
Ventajas:
Desventajas:
Idea clave: En lugar de centrarse en la posición absoluta, se enfoca en la distancia relativa entre las palabras.
Fondo: El significado de una palabra en el lenguaje natural a menudo se ve más influenciado por su relación con las palabras cercanas que por su posición absoluta. Además, el codificado posicional absoluto tiene la desventaja de no capturar eficazmente las relaciones entre palabras distantes.
2.1 Extensión matemática:
aquí \(a_{i-j} \in \mathbb{R}^d\) es un vector aprendible para la posición relativa \(i-j\).
Rotary Positional Encoding (RoPE): utiliza matrices de rotación para codificar posiciones relativas.
\(\text{RoPE}(x, m) = x \odot e^{im\theta}\)
aquí \(\theta\) es un hiperparámetro que controla la frecuencia, y \(\odot\) denota multiplicación compleja (o la matriz de rotación correspondiente).
Versión simplificada de T5: utiliza un sesgo aprendible \(b\) para posiciones relativas, y recorta (clipping) los valores si la distancia relativa excede un rango determinado.
\(e_{ij} = \frac{x_iW^Q(x_jW^K)^T + b_{\text{clip}(i-j)}}{\sqrt{d}}\)
\(b \in \mathbb{R}^{2k+1}\) es un vector de sesgo para posiciones relativas recortadas [-k, k].
Ventajas:
Desventajas:
3.1 Aplicación de convolución por profundidad: realiza convoluciones independientes en cada canal para reducir el número de parámetros y mejorar la eficiencia computacional. \(P(i) = \sum_{k=-K}^K w_k \cdot x_{i+k}\)
aquí \(K\) es el tamaño del kernel, y \(w_k\) son pesos aprendibles.
3.2 Convoluciones multi-escala: similar a ResNet, utiliza canales de convolución paralelos para capturar información posicional en diferentes rangos.
\(P(i) = \text{Concat}(\text{Conv}_{3x1}(x), \text{Conv}_{5x1}(x))\)
4.1 Codificación basada en LSTM: utiliza una red LSTM para codificar información de posición secuencial.
\(h_t = \text{LSTM}(x_t, h_{t-1})\) \(P(t) = W_ph_t\)
4.2 Variante más reciente: Neural ODE: modela dinámicas en tiempo continuo para superar las limitaciones de la LSTM discreta.
\(\frac{dh(t)}{dt} = f_\theta(h(t), t)\) \(P(t) = \int_0^t f_\theta(h(\tau), \tau)d\tau\)
5.1 Representación de embeddings complejos: representa la información de posición en forma compleja.
\(z(i) = r(i)e^{i\phi(i)}\)
aquí \(r\) es la magnitud de la posición, y \(\phi\) es el ángulo de fase.
5.2 Teorema de desplazamiento de fase: representa el desplazamiento de posición como una rotación en el plano complejo.
\(z(i+j) = z(i) \cdot e^{i\omega j}\)
aquí \(\omega\) es un parámetro de frecuencia aprendible.
6.1 Codificado posicional compuesto: \(P(i)=αP_{abs}(i)+βP_{rel}(i)\)
\(P(i)=αP_{abs} (i)+βP_{rel}(i)\) α, β = pesos de aprendizaje
6.2 Codificación Posicional Dinámica:
\(P(i) = \text{MLP}(i, \text{Context})\) Aprendizaje de representaciones posicionales dependientes del contexto
A continuación se presentan los resultados de la comparación de rendimiento experimental de diferentes enfoques de codificación posicional en el benchmark GLUE. (El rendimiento real puede variar según la estructura del modelo, los datos y la configuración de los hiperparámetros).
| Método | Precisión | Tiempo de inferencia (ms) | Uso de memoria (GB) |
|---|---|---|---|
| Absoluto (Senoidal) | 88.2 | 12.3 | 2.1 |
| Relativo (RoPE) | 89.7 | 14.5 | 2.4 |
| CNN Multiescala | 87.9 | 13.8 | 3.2 |
| Complejo (CLEX) | 90.1 | 15.2 | 2.8 |
| PE Dinámico | 90.3 | 17.1 | 3.5 |
Recientemente, se han estado investigando nuevas técnicas de codificación posicional inspiradas en sistemas cuánticos y biológicos.
Características de teoría de grupos de RoPE:
Representación del grupo de rotación SO(2): \(R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\)
Esta propiedad garantiza la preservación de la posición relativa en las puntuaciones de atención.
Cálculo eficiente del sesgo de posición relativa:
Uso de la estructura de matriz Toeplitz: \(B = [b_{i-j}]_{i,j}\)
Implementación posible con complejidad \(O(n\log n)\) utilizando FFT.
Flujo de gradiente de PE complejo:
Aplicación de las reglas de diferenciación de Wirtinger: \(\frac{\partial L}{\partial z} = \frac{1}{2}\left(\frac{\partial L}{\partial \text{Re}(z)} - i\frac{\partial L}{\partial \text{Im}(z)}\right)\)
Conclusión: La codificación posicional es un elemento clave que tiene un gran impacto en el rendimiento del modelo de transformadores y ha evolucionado de diversas maneras más allá de las funciones simples de seno-coseno. Cada método tiene sus propias ventajas y desventajas, así como fundamentos matemáticos, y es importante seleccionar el método adecuado según las características y requisitos del problema. Recientemente, se han estado investigando nuevas técnicas de codificación posicional inspiradas en diversos campos, como la computación cuántica y la biología, lo que sugiere un desarrollo continuo esperado en el futuro.
Hasta ahora hemos examinado cómo se han desarrollado los componentes clave del transformer. Ahora veamos cómo estos elementos se integran en una arquitectura completa. Esta es la arquitectura completa del transformer.

Fuente de la figura: The Illustrated Transformer (Jay Alammar, 2018) Licencia CC BY 4.0
El código de implementación del transformer para fines educativos se encuentra en chapter_08/transformer. Esta implementación se basa y modifica The Annotated Transformer del grupo Harvard NLP. Los principales cambios son los siguientes.
TransformerConfig: Se ha introducido una clase separada para configurar el modelo, facilitando la gestión de hiperparámetros.nn.ModuleList para hacer que el código sea más conciso e intuitivo.El transformer está compuesto principalmente por un codificador (Encoder) y un decodificador (Decoder), con los siguientes componentes:
| Componente | Codificador | Decodificador |
|---|---|---|
| Atención multi-cabeza | Atención a sí misma (Self-Attention) | Atención a sí misma enmascarada (Masked Self-Attention) |
| Atención codificador-decodificador (Encoder-Decoder Attention) | ||
| Red de alimentación hacia adelante | Aplicado independientemente en cada posición | Aplicado independientemente en cada posición |
| Conexión residual | Suma la entrada y salida de cada subcapa (atención, feed-forward) | Suma la entrada y salida de cada subcapa (atención, feed-forward) |
| Normalización de capa | Aplicada a la entrada de cada subcapa (Pre-LN) | Aplicada a la entrada de cada subcapa (Pre-LN) |
Capa del codificador - código
class TransformerEncoderLayer(nn.Module):
def __init__(self, config):
super().__init__()
self.attention = MultiHeadAttention(config)
self.feed_forward = FeedForward(config)
# SublayerConnection for Pre-LN structure
self.sublayer = nn.ModuleList([
SublayerConnection(config) for _ in range(2)
])
def forward(self, x, attention_mask=None):
x = self.sublayer[0](x, lambda x: self.attention(x, x, x, attention_mask))
x = self.sublayer[1](x, self.feed_forward)
return xAtención Multi-Cabeza (Multi-Head Attention): calcula las relaciones entre todas las posiciones de la secuencia de entrada en paralelo. Cada cabeza analiza la secuencia desde una perspectiva diferente y sintetiza los resultados para capturar información contextual rica. (“The cat sits on the mat” ejemplo donde diferentes cabezas aprenden relaciones sujeto-verbo, frase preposicional, artículo-sustantivo, etc.)
class FeedForward(nn.Module):
def __init__(self, config):
super().__init__()
self.linear1 = nn.Linear(config.hidden_size, config.intermediate_size)
self.linear2 = nn.Linear(config.intermediate_size, config.hidden_size)
self.activation = nn.GELU()
def forward(self, x):
x = self.linear1(x)
x = self.activation(x)
x = self.linear2(x)
return xLa razón por la que se necesita una red feedforward está relacionada con la densidad de información de las salidas de atención. El resultado de la operación de atención (\(\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d\_k}})V\)) es una suma ponderada de los vectores \(V\), donde la información contextual está concentrada en \(d\_{model}\) dimensiones (512 en el artículo). Si se aplica directamente la función de activación ReLU, gran parte de esta información concentrada puede perderse (ReLU convierte los valores negativos en 0). Por lo tanto, la red feedforward primero expande las \(d\_{model}\) dimensiones a una dimensión mayor (\(4 \times d\_{model}\), 2048 en el artículo) para ampliar el espacio de representación, luego aplica ReLU (o GELU) y vuelve a reducir la dimensionalidad a la original, añadiendo no linealidad.
x = W1(x) # hidden_size -> intermediate_size (512 -> 2048)
x = ReLU(x) # or GELU
x = W2(x) # intermediate_size -> hidden_size (2048 -> 512)Conexión residual (Residual Connection): Se trata de sumar la entrada y la salida de cada subcapa (atención multi-cabeza o red feedforward). Esto ayuda a mitigar el problema de desvanecimiento/explotación del gradiente y facilita el aprendizaje en redes profundas. (Consulte el Capítulo 7 sobre conexiones residuales).
Normalización de capa (Layer Normalization): Se aplica a la entrada de cada subcapa (Pre-LN).
class LayerNorm(nn.Module):
def __init__(self, config):
super().__init__()
self.gamma = nn.Parameter(torch.ones(config.hidden_size))
self.beta = nn.Parameter(torch.zeros(config.hidden_size))
self.eps = config.layer_norm_eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = (x - mean).pow(2).mean(-1, keepdim=True).sqrt()
return self.gamma * (x - mean) / (std + self.eps) + self.betaLa normalización de capas es una técnica propuesta en el paper “Layer Normalization” de Ba, Kiros y Hinton en 2016. Mientras que la normalización por lotes (Batch Normalization) realiza la normalización a lo largo de la dimensión del lote, la normalización de capas calcula la media y la varianza a lo largo de la dimensión de características de cada muestra para realizar la normalización.
Ventajas de la normalización de capas
En el caso del Transformer, se utiliza el método Pre-LN para aplicar la normalización de capas antes de pasar por cada subcapa (atención multi-cabeza, red feed-forward).
Visualización de la normalización de capas
from dldna.chapter_08.visualize_layer_norm import visualize_layer_normalization
visualize_layer_normalization()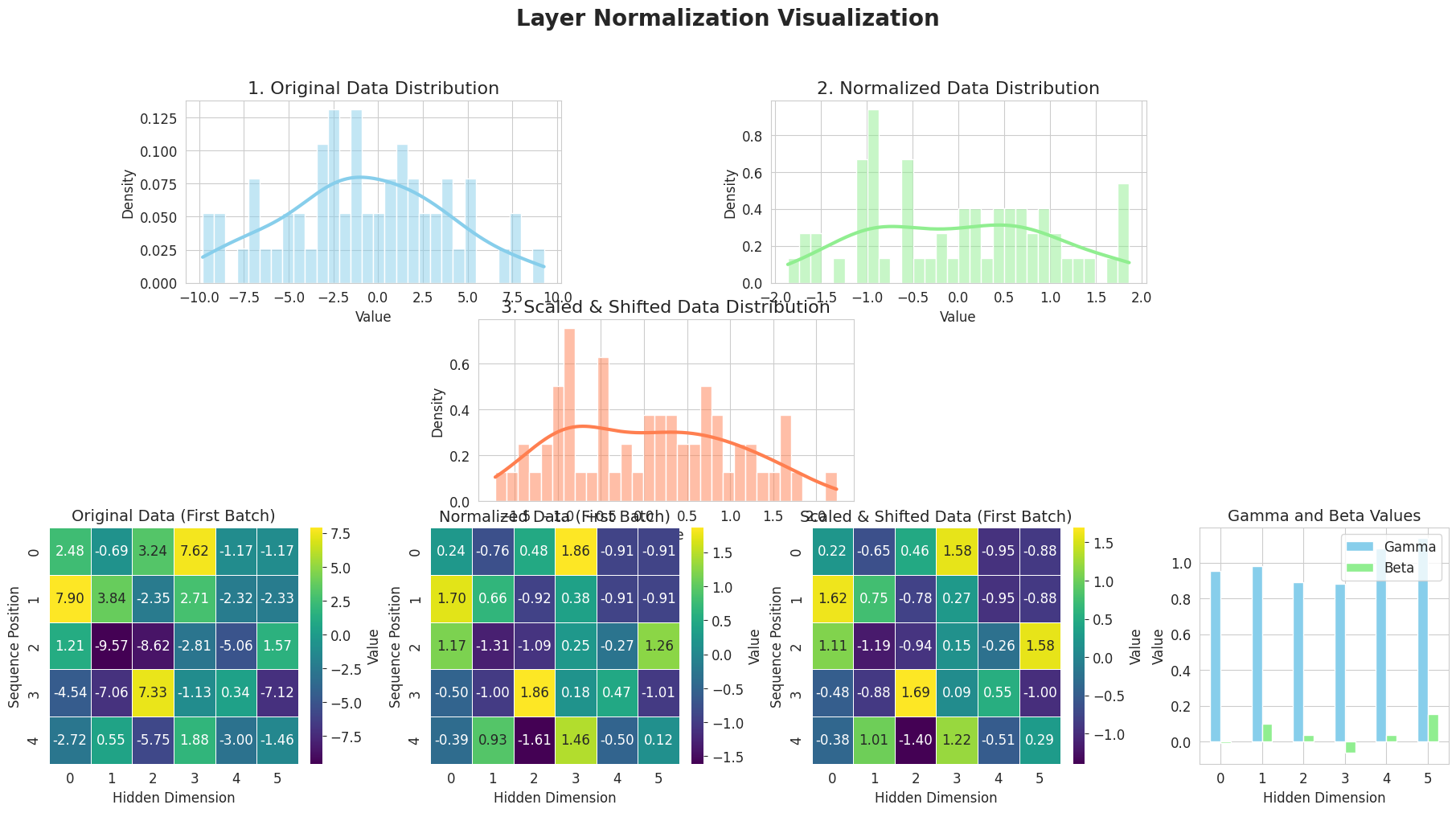
========================================
Input Data Shape: (2, 5, 6)
Mean Shape: (2, 5, 1)
Standard Deviation Shape: (2, 5, 1)
Normalized Data Shape: (2, 5, 6)
Gamma (Scale) Values:
[0.95208258 0.9814341 0.8893665 0.88037934 1.08125258 1.135624 ]
Beta (Shift) Values:
[-0.00720101 0.10035329 0.0361636 -0.06451198 0.03613956 0.15380366]
Scaled & Shifted Data Shape: (2, 5, 6)
========================================La imagen anterior muestra cómo funciona la normalización de capa (Layer Normalization) paso a paso.
De esta manera, la normalización de capa normaliza las entradas de cada capa para mejorar la estabilidad y velocidad del aprendizaje.
Clave:
Esta combinación de componentes (atención multi-cabeza, red feedforward, conexión residual, normalización de capa) maximiza las ventajas de cada elemento. La atención multi-cabeza captura diversos aspectos de la secuencia de entrada, la red feedforward añade no linealidad, y las conexiones residuales y la normalización de capa permiten un aprendizaje estable incluso en redes profundas.
El transformador tiene una estructura de codificador-decodificador para la traducción automática. El codificador comprende el idioma de origen (por ejemplo, inglés) y el decodificador genera el idioma objetivo (por ejemplo, francés). Aunque el codificador y el decodificador comparten componentes básicos como la atención multi-cabeza y las redes feedforward, están configurados de manera diferente para adaptarse a sus respectivos propósitos.
Comparación de la composición del codificador vs. decodificador
| Componente | Codificador | Decodificador |
|---|---|---|
| Número de capas de atención | 1 (autoatención) | 2 (autoatención enmascarada, atención codificador-decodificador) |
| Estrategia de máscara | Solo utiliza máscaras de relleno | Máscaras de relleno + máscaras de causalidad |
| Procesamiento contextual | Procesamiento de contexto bidireccional | Procesamiento de contexto unidireccional (autoregresivo) |
| Referencia de entrada | Solo se refiere a su propia entrada | Se refiere a su propia entrada + salida del codificador |
A continuación, se resumen varios términos de atención.
Resumen de conceptos de atención
| Tipo de atención | Características | Ubicación de descripción | Concepto clave |
|---|---|---|---|
| Atención (básica) | - Cálculo de similitud mediante vectores de palabras idénticos - Generación de información contextual a través de una simple suma ponderada - Versión simplificada para aplicar en modelos seq2seq |
8.2.2 | - Cálculo de similitud mediante producto interno de vectores de palabras - Conversión de pesos con softmax - Aplicación de máscaras de relleno a toda la atención |
| Autoatención (Self-Attention) | - Separación del espacio Q, K, V - Optimización independiente en cada espacio - La secuencia de entrada se refiere a sí misma - Utilizado en el codificador |
8.2.3 | - Separación de roles para cálculo de similitud y transmisión de información - Transformaciones aprendibles Q, K, V - Posibilidad de procesamiento contextual bidireccional |
| Autoatención enmascarada | - Bloqueo de información futura - Uso de máscaras causales - Utilizado en el decodificador |
8.2.5 | - Máscara triangular superior para bloquear la información futura - Posibilidad de generación autoregresiva - Procesamiento contextual unidireccional |
| Atención cruzada (codificador-decodificador) | - Query: estado del decodificador - Key, Value: salida del codificador - También llamada atención cruzada - Utilizado en el decodificador |
8.4.3 | - El decodificador hace referencia a la información del codificador - Cálculo de relaciones entre dos secuencias - Refleja el contexto durante la traducción/generación |
En el transformador, se utilizan los nombres autoatención, enmascarada y cruzada. Mecanismos de atención son idénticos y se distinguen según la fuente de Q, K, V.
Componentes del codificador | Componente | Descripción | | —————————- | ——————————————————————————————— | | Embeddings | Convierte los tokens de entrada en vectores y agrega información de posición para codificar el significado y el orden de la secuencia de entrada. | | TransformerEncoderLayer (x N) | Apila múltiples capas de la misma capa para extraer características más abstractas y complejas de forma jerárquica a partir de la secuencia de entrada. | | LayerNorm | Normaliza la distribución de las características de la salida final para estabilizarla y prepararla en un formato útil para el decodificador. |
class TransformerEncoder(nn.Module):
def __init__(self, config):
super().__init__()
self.embeddings = Embeddings(config)
self.layers = nn.ModuleList([
TransformerEncoderLayer(config)
for _ in range(config.num_hidden_layers)
])
self.norm = LayerNorm(config)
def forward(self, input_ids, attention_mask=None):
x = self.embeddings(input_ids)
for i, layer in enumerate(self.layers):
x = layer(x, attention_mask)
output = self.norm(x)
return outputEl codificador está compuesto por una capa de incrustación, múltiples capas de codificador y una capa de normalización final.
1. Mecanismo de autoatención (ejemplo)
La autoatención del codificador calcula las relaciones entre todas las pares de palabras en la secuencia de entrada para enriquecer la información contextual de cada palabra.
2. Importancia de la posición del dropout
El dropout desempeña un papel crucial para prevenir el sobreajuste y mejorar la estabilidad del aprendizaje. En el codificador de transformers, se aplica dropout en las siguientes posiciones.
Este esquema de aplicación de dropout regula el flujo de información, evita que el modelo dependa excesivamente de ciertas características y mejora el rendimiento generalización.
3. Estructura de pila del codificador
El codificador de transformers tiene una estructura en la que se apilan (stack) varias capas de codificador con la misma arquitectura.
Cuanto más profundas son las capas, más características abstractas y complejas pueden aprender. Investigaciones posteriores han permitido el desarrollo de modelos con muchas más capas gracias a los avances en hardware y técnicas de aprendizaje (Pre-LayerNorm, recorte de gradientes, calentamiento del tasa de aprendizaje, aprendizaje de precisión mixta, acumulación de gradientes), como BERT-base: 12 capas, GPT-3: 96 capas, PaLM: 118 capas.
4. Salida final del codificador y uso en el decodificador
La salida final del codificador es una representación vectorial que contiene información contextual rica para cada token de entrada. Esta salida se utiliza como Key y Value en la atención codificador-decodificador (Cross-Attention) del decodificador. El decodificador genera cada token de la secuencia de salida consultando la salida del codificador, lo que permite una traducción/creación precisa considerando el contexto de la oración original.
El decodificador es similar al codificador, pero difiere en que genera la salida de manera autoregresiva (autoregressive).
Código completo de la capa del decodificador
class TransformerDecoderLayer(nn.Module):
def __init__(self, config):
super().__init__()
self.self_attn = MultiHeadAttention(config)
self.cross_attn = MultiHeadAttention(config)
self.feed_forward = FeedForward(config)
# Pre-LN을 위한 레이어 정규화
self.norm1 = LayerNorm(config)
self.norm2 = LayerNorm(config)
self.norm3 = LayerNorm(config)
self.dropout = nn.Dropout(config.dropout_prob)
def forward(self, x, memory, src_mask=None, tgt_mask=None):
# Pre-LN 구조
m = self.norm1(x)
x = x + self.dropout(self.self_attn(m, m, m, tgt_mask))
m = self.norm2(x)
x = x + self.dropout(self.cross_attn(m, memory, memory, src_mask))
m = self.norm3(x)
x = x + self.dropout(self.feed_forward(m))
return xComponentes principales del decodificador y sus roles
| Subcapa | Rol | Características de implementación |
|---|---|---|
| Atención propia enmascarada | Identificar las relaciones entre las palabras dentro de la secuencia de salida generada hasta el momento, evitar la referencia a información futura (generación autoregresiva) | tgt_mask (máscara causal + máscara de padding) usada, self.self_attn |
| Atención codificador-decodificador (atención cruzada) | El decodificador se refiere a la salida del codificador (información contextual de la oración de entrada) para obtener información relevante al palabra actual que se está generando | Q: decodificador, K, V: codificador, src_mask (máscara de padding) usada, self.cross_attn |
| Red de alimentación hacia adelante | Transformar independientemente las representaciones en cada posición para generar representaciones más ricas | Estructura idéntica a la del codificador, self.feed_forward |
| Normalización de capa (LayerNorm) | Normalizar la entrada de cada subcapa (Pre-LN), mejorar la estabilidad y rendimiento del aprendizaje | self.norm1, self.norm2, self.norm3 |
| Apagado aleatorio (Dropout) | Prevenir el sobreajuste, mejorar el rendimiento generalización | Aplicada a la salida de cada subcapa, self.dropout |
| Conexión residual (Residual Connection) | Mitigar problemas de desvanecimiento/explotación del gradiente en redes profundas, mejorar el flujo de información | Sumar la entrada y la salida de cada subcapa |
1. Atención propia enmascarada (Masked Self-Attention) * Rol: El decodificador genera la salida de manera autoregresiva (autoregressive), es decir, no puede hacer referencia a las palabras que futuras aparecerán después de la palabra actualmente en generación. Por ejemplo, al traducir “I love you”, una vez generado “yo” y al generar “te”, no se puede acceder al token “amo” que aún no ha sido generado. * Implementación: Se utiliza tgt_mask, que combina una máscara de causalidad (causal mask) y una máscara de padding. La máscara de causalidad llena la parte superior triangular de la matriz con -inf para hacer que los pesos de atención a tokens futuros sean 0 (ver sección 8.2.5). En el método forward de TransformerDecoderLayer, esta máscara se aplica en la parte self.self_attn(m, m, m, tgt_mask).
2. Atención codificador-decodificador (Cross-Attention)
memory)memory)src_mask (máscara de padding) para ignorar los tokens de padding en la salida del codificador.forward de TransformerDecoderLayer, esta atención se realiza en la parte self.cross_attn(m, memory, memory, src_mask). memory representa la salida del codificador.3. Estructura de pila del decodificador
class TransformerDecoder(nn.Module):
def __init__(self, config):
super().__init__()
self.embeddings = Embeddings(config)
self.layers = nn.ModuleList([
TransformerDecoderLayer(config)
for _ in range(config.num_hidden_layers)
])
self.norm = LayerNorm(config)
def forward(self, x, memory, src_mask=None, tgt_mask=None):
x = self.embeddings(x)
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)TransformerDecoderLayer (6 capas en el artículo original).forward de la clase TransformerDecoder recibe como entrada x (entrada del decodificador), memory (salida del codificador), src_mask (máscara de padding del codificador) y tgt_mask (máscara del decodificador), pasa secuencialmente a través de las capas del decodificador y devuelve la salida final.Número de capas de codificador/decodificador por modelo
| Modelo | Año | Estructura | Capas de codificador | Capas de decodificador | Parámetros totales |
|---|---|---|---|---|---|
| Transformer original | 2017 | Codificador-decodificador | 6 | 6 | 65M |
| BERT-base | 2018 | Solo codificador | 12 | - | 110M |
| GPT-2 | 2019 | Solo decodificador | - | 48 | 1.5B |
| T5-base | 2020 | Codificador-decodificador | 12 | 12 | 220M |
| GPT-3 | 2020 | Solo decodificador | - | 96 | 175B |
| PaLM | 2022 | Solo decodificador | - | 118 | 540B |
| Gemma-2 | 2024 | Solo decodificador | - | 18-36 | 2B-27B |
Los modelos recientes pueden aprender eficazmente un mayor número de capas gracias a técnicas avanzadas de aprendizaje como Pre-LN. Los decodificadores más profundos pueden aprender patrones lingüísticos más abstractos y complejos, lo que ha llevado a mejoras en el rendimiento en tareas de procesamiento de lenguaje natural como la traducción y la generación de texto.
4. Generación de salida del decodificador y condiciones de finalización
generator (capa lineal) de la clase Transformer convierte la salida final del decodificador en un vector de logit de tamaño de vocabulario (vocab_size) y aplica log_softmax para obtener la distribución de probabilidad de cada token. Se predice el siguiente token basado en esta distribución de probabilidad.# 최종 출력 생성 (설명용)
output = self.generator(decoder_output)
return F.log_softmax(output, dim=-1)<eos>, </s> etc.). El decodificador aprende durante el proceso de entrenamiento a agregar este token especial al final de las frases.En general, aunque no están incluidas en el decodificador, las estrategias de generación de tokens pueden influir en los resultados de la salida generada.
| Estrategia de generación | Cómo funciona | Ventajas | Desventajas | Ejemplo |
|---|---|---|---|---|
| Greedy Search | En cada paso, selecciona el token con la probabilidad más alta. | Rápido, implementación simple | Posibilidad de solución subóptima local, falta de diversidad | “Yo” siguiente → “voy a la escuela” (máxima probabilidad) |
| Beam Search | Seguimiento simultáneo de k caminos. |
Búsqueda amplia, posibilidad de mejores resultados | Costo computacional alto, diversidad limitada | k=2: mantener “Yo voy a la escuela”, “Yo voy a casa” y proceder al siguiente paso |
| Top-k Sampling | Selecciona proporcionalmente según la probabilidad entre los k tokens más probables. |
Diversidad adecuada, evita tokens extraños | Dificultad en establecer el valor de k, rendimiento dependiente del contexto |
k=3: “Yo” siguiente → {“voy a la escuela”, “voy a casa”, “voy al parque”} seleccionado según la probabilidad |
| Nucleus Sampling | Selecciona entre los tokens cuya probabilidad acumulada no excede p. |
Grupo de candidatos dinámico, flexible con el contexto | Necesidad de ajustar el valor de p, aumento de complejidad computacional |
p=0.9: “Yo” siguiente → {“voy a la escuela”, “voy a casa”, “voy al parque”, “como”} seleccionado sin exceder una probabilidad acumulada de 0.9 |
| Temperature Sampling | Ajuste de la distribución de probabilidad (baja para ser más seguro, alta para ser más diverso). | Regulación de la creatividad de la salida, implementación simple | Demasiado alto puede resultar inapropiado, demasiado bajo puede generar texto repetitivo | T=0.5: enfatiza las altas probabilidades, T=1.5: aumenta la posibilidad de seleccionar bajas probabilidades |
Estas estrategias de generación de tokens se implementan generalmente como clases o funciones separadas del decodificador.
Hasta ahora hemos entendido el propósito del diseño y el principio de funcionamiento del transformer. Con base en lo explicado hasta el 8.4.3, examinaremos la estructura completa del transformer. La implementación se ha modificado estructuralmente, incluyendo modularización, basándose en el contenido de Havard NLP, y se ha redactado de manera lo más concisa posible para fines educativos. En un entorno de producción real, se necesitarían adiciones como tipado de tipos para la estabilidad del código, procesamiento eficiente de tensores multidimensionales, validación de entrada y manejo de errores, optimización de memoria, y escalabilidad para soportar diversas configuraciones.
El código está en el directorio chapter_08/transformer.
Función e implementación de la capa de incrustación
La primera etapa del transformer es la capa de incrustación, que convierte los tokens de entrada en un espacio vectorial. La entrada es una secuencia de IDs de tokens enteros (por ejemplo: [101, 2045, 3012, …]), donde cada ID de token es un índice único del diccionario léxico. La capa de incrustación mapea estos IDs a vectores de alta dimensión (vectores de incrustación).
La dimensión de incrustación tiene un gran impacto en el rendimiento del modelo. Una dimensión grande puede representar información semántica rica, pero aumenta el costo computacional, mientras que una dimensión pequeña tiene el efecto contrario.
Tras pasar por la capa de incrustación, las dimensiones del tensor cambian de la siguiente manera:
A continuación se muestra un ejemplo de código para realizar incrustaciones en el transformer.
import torch
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.embeddings import Embeddings
# Create a configuration object
config = TransformerConfig()
config.vocab_size = 1000 # Vocabulary size
config.hidden_size = 768 # Embedding dimension
config.max_position_embeddings = 512 # Maximum sequence length
# Create an embedding layer
embedding_layer = Embeddings(config)
# Generate random input tokens
batch_size = 2
seq_length = 4
input_ids = torch.tensor([
[1, 5, 9, 2], # First sequence
[6, 3, 7, 4] # Second sequence
])
# Perform embedding
embedded = embedding_layer(input_ids)
print(f"Input shape: {input_ids.shape}")
# Output: Input shape: torch.Size([2, 4])
print(f"Shape after embedding: {embedded.shape}")
# Output: Shape after embedding: torch.Size([2, 4, 768])
print("\nPart of the embedding vector for the first token of the first sequence:")
print(embedded[0, 0, :10]) # Print only the first 10 dimensionsInput shape: torch.Size([2, 4])
Shape after embedding: torch.Size([2, 4, 768])
Part of the embedding vector for the first token of the first sequence:
tensor([-0.7838, -0.9194, 0.4240, -0.8408, -0.0876, 2.0239, 1.3892, -0.4484,
-0.6902, 1.1443], grad_fn=<SliceBackward0>)Clase de configuración
La clase TransformerConfig define todos los hiperparámetros del modelo.
class TransformerConfig:
def __init__(self):
self.vocab_size = 30000 # Vocabulary size
self.hidden_size = 768 # Hidden layer dimension
self.num_hidden_layers = 12 # Number of encoder/decoder layers
self.num_attention_heads = 12 # Number of attention heads
self.intermediate_size = 3072 # FFN intermediate layer dimension
self.hidden_dropout_prob = 0.1 # Hidden layer dropout probability
self.attention_probs_dropout_prob = 0.1 # Attention dropout probability
self.max_position_embeddings = 512 # Maximum sequence length
self.layer_norm_eps = 1e-12 # Layer normalization epsilonvocab_size es el número total de tokens únicos que el modelo puede manejar. Aquí, para una implementación simple, asumimos la tokenización a nivel de palabras y lo establecemos en 30,000. En modelos de lenguaje reales, se utilizan diversos tokenizadores subpalabra como BPE (Byte Pair Encoding), Unigram, WordPiece, etc., y en este caso, vocab_size puede ser menor. Por ejemplo, la palabra ‘playing’ puede descomponerse en ‘play’ e ‘ing’, lo que permite representarla con solo dos subpalabras.
Cambio de dimensiones del tensor de atención
En la atención multi-cabeza, cada cabeza reorganiza las dimensiones del tensor de entrada para calcular la atención de manera independiente.
class MultiHeadAttention(nn.Module):
def forward(self, query, key, value, mask=None):
batch_size = query.size(0)
# Linear transformations and head splitting
query = self.linears[0](query).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
key = self.linears[1](key).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
value = self.linears[2](value).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)El proceso de transformación dimensional es el siguiente:
view: (batch_size, seq_len, h, d_k)transpose: (batch_size, h, seq_len, d_k)Aquí, h es el número de cabezas y d_k es la dimensión de cada cabeza (d_model / h). A través de este reordenamiento dimensional, cada cabeza calcula la atención de manera independiente.
Estructura integrada del transformador
Finalmente, examinemos la clase Transformer que integra todos los componentes.
class Transformer(nn.Module):
def __init__(self, config: TransformerConfig):
super().__init__()
self.encoder = TransformerEncoder(config)
self.decoder = TransformerDecoder(config)
self.generator = nn.Linear(config.hidden_size, config.vocab_size)
self._init_weights()El transformador consta de tres componentes principales.
El método forward procesa los datos en el siguiente orden.
def forward(self, src, tgt, src_mask=None, tgt_mask=None):
# Encoder-decoder processing
encoder_output = self.encode(src, src_mask)
decoder_output = self.decode(encoder_output, src_mask, tgt, tgt_mask)
# Generate final output
output = self.generator(decoder_output)
return F.log_softmax(output, dim=-1)El cambio de dimensiones del tensor es el siguiente:
src, tgt): (batch_size, seq_len)En la siguiente sección aplicaremos esta estructura a un ejemplo práctico.
Hasta ahora hemos examinado la estructura y el principio de funcionamiento del transformer. Ahora, a través de ejemplos prácticos, veremos cómo funciona el transformer. Los ejemplos están organizados en orden de dificultad, y cada uno está diseñado para ayudar a comprender una función específica del transformer. Estos ejemplos muestran métodos para resolver gradualmente diversos problemas de procesamiento de datos y diseño de modelos que pueden encontrarse en proyectos reales. En particular, abordan temas prácticos como el preprocesamiento de datos, el diseño de funciones de pérdida y la configuración de métricas de evaluación. La ubicación de los ejemplos es transformer/examples.
examples
├── addition_task.py # 8.5.2 Tarea de suma
├── copy_task.py # 8.5.1 Tarea de copia simple
└── parser_task.py # 8.5.3 Tarea de análisis sintácticoLo que se aprende en cada ejemplo es lo siguiente.
Tarea de copia simple: permite comprender las funciones básicas del transformer. A través de la visualización de patrones de atención, se puede entender claramente el principio de funcionamiento del modelo. Además, se pueden aprender métodos básicos de procesamiento de datos secuenciales, diseño de dimensiones de tensores para procesamiento por lotes, estrategias básicas de padding y masking, y diseño de funciones de pérdida especializadas en la tarea.
Problema de suma posicional: muestra cómo es posible la generación autoregresiva. Se puede observar claramente el proceso de generación secuencial del decodificador y el papel de la atención cruzada. Además, proporciona experiencia práctica en tokenización de datos numéricos, métodos para generar conjuntos de datos válidos, evaluación de precisión parcial/completa, y pruebas de rendimiento generalizado según la expansión posicional.
Tarea de análisis sintáctico: muestra cómo el transformer aprende y expresa relaciones estructurales. Se puede entender cómo el mecanismo de atención captura la estructura jerárquica de secuencias de entrada. Además, se pueden adquirir diversas técnicas necesarias para problemas de análisis sintáctico prácticos, como la transformación de datos estructurados en secuencias, diseño de vocabulario de tokens, estrategias de linealización de estructuras de árboles y métodos de evaluación de precisión estructural.
A continuación se muestra una tabla que resume lo que se aprende en cada ejemplo:
| Ejemplo | Contenido de aprendizaje |
|---|---|
| 8.5.1 Tarea de copia simple (copy_task.py) | - Comprensión de las funciones básicas y el principio de funcionamiento del transformer - Comprensión intuitiva a través de la visualización de patrones de atención - Métodos de procesamiento de datos secuenciales y diseño de dimensiones de tensores para procesamiento por lotes - Estrategias básicas de padding y masking, y diseño de funciones de pérdida especializadas en la tarea |
| 8.5.2 Tarea de suma posicional (addition_task.py) | - Comprensión de cómo es posible la generación autoregresiva - Observación del proceso de generación secuencial del decodificador y el papel de la atención cruzada - Tokenización de datos numéricos, métodos para generar conjuntos de datos válidos - Evaluación de precisión parcial/completa, pruebas de rendimiento generalizado según la expansión posicional |
| 8.5.3 Tarea de análisis sintáctico (parser_task.py) | - Comprensión de cómo el transformer aprende y expresa relaciones estructurales - Comprensión del mecanismo de atención que captura la estructura jerárquica de secuencias de entrada - Transformación de datos estructurados en secuencias, diseño de vocabulario de tokens - Estrategias de linealización de estructuras de árboles, métodos de evaluación de precisión estructural |
El primer ejemplo es una tarea de copia que reproduce la secuencia de entrada tal cual. Esta tarea es adecuada para verificar el funcionamiento básico del transformer y visualizar los patrones de atención, aunque parezca sencilla, es muy útil para comprender los mecanismos centrales del transformer.
Preparación de datos
Los datos para la tarea de copia consisten en secuencias idénticas de entrada y salida. A continuación se muestra un ejemplo de generación de datos:
El primer ejemplo es una tarea de copia que reproduce la secuencia de entrada tal cual. Esta tarea es adecuada para verificar el funcionamiento básico del transformer y visualizar los patrones de atención, aunque parezca sencilla, es muy útil para comprender los mecanismos centrales del transformer.
Preparación de datos
Los datos para la tarea de copia consisten en secuencias idénticas de entrada y salida. A continuación se muestra un ejemplo de generación de datos:
from dldna.chapter_08.transformer.examples.copy_task import explain_copy_data
explain_copy_data(seq_length=5)
=== Copy Task Data Explanation ===
Sequence Length: 5
1. Input Sequence:
Original Tensor Shape: torch.Size([1, 5])
Input Sequence: [7, 15, 2, 3, 12]
2. Target Sequence:
Original Tensor Shape: torch.Size([1, 5])
Target Sequence: [7, 15, 2, 3, 12]
3. Task Description:
- Basic task of copying the input sequence as is
- Tokens at each position are integer values between 1-19
- Input and output have the same sequence length
- Current Example: [7, 15, 2, 3, 12] → [7, 15, 2, 3, 12]create_copy_data genera un tensor de salida idéntico al tensor de entrada para el aprendizaje. Crea un tensor bidimensional (batch_size, seq_length) para el procesamiento por lotes, donde cada elemento es un valor entero entre 1 y 19.
def create_copy_data(batch_size: int = 32, seq_length: int = 5) -> torch.Tensor:
"""복사 태스크용 데이터 생성"""
sequences = torch.randint(1, 20, (batch_size, seq_length))
return sequences, sequencesEste ejemplo de datos es idéntico a los datos de entrada tokenizados utilizados en el procesamiento de lenguaje natural y modelado de secuencias. En el procesamiento de lenguaje, cada token se convierte en un valor entero único antes de ser ingresado al modelo.
Entrenamiento del modelo
Se entrena el modelo con el siguiente código.
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.copy_task import train_copy_task
seq_length = 20
config = TransformerConfig()
# Modify default values
config.vocab_size = 20 # Small vocabulary size (minimum size to represent integers 1-19)
config.hidden_size = 64 # Small hidden dimension (enough representation for a simple task)
config.num_hidden_layers = 2 # Minimum number of layers (considering the low complexity of the copy task)
config.num_attention_heads = 2 # Minimum number of heads (minimum configuration for attention from various perspectives)
config.intermediate_size = 128 # Small FFN dimension (set to twice the hidden dimension to ensure adequate transformation capacity)
config.max_position_embeddings = seq_length # Short sequence length (set to the same length as the input sequence)
model = train_copy_task(config, num_epochs=50, batch_size=40, steps_per_epoch=100, seq_length=seq_length)
=== Start Training ====
Device: cuda:0
Model saved to saved_models/transformer_copy_task.pthPrueba del modelo
Se lee el modelo de entrenamiento almacenado y se realiza la prueba.
from dldna.chapter_08.transformer.examples.copy_task import test_copy
test_copy(seq_length=20)
=== Copy Test ===
Input: [10, 10, 2, 12, 1, 5, 3, 1, 8, 18, 2, 19, 2, 2, 8, 14, 7, 19, 5, 4]
Output: [10, 10, 2, 12, 1, 5, 3, 1, 8, 18, 2, 19, 2, 2, 8, 14, 7, 19, 5, 4]
Accuracy: TrueConfiguración del modelo
hidden_size: 64 (dimensión de diseño del modelo, d_model).
intermediate_size: Tamaño del FFN, que debe ser suficientemente grande en comparación con d_model.Implementación de máscaras
El transformer utiliza dos tipos de máscaras.
seq_length) y no requieren relleno, pero se incluye para ilustrar el uso general del transformer.create_pad_mask (en PyTorch, nn.Transformer o en la biblioteca transformers de Hugging Face, esta función está implementada internamente).src_mask = create_pad_mask(src).to(device)create_subsequent_mask genera una máscara en forma de matriz triangular superior que oculta los tokens posteriores a la posición actual.tgt_mask = create_subsequent_mask(decoder_input.size(1)).to(device)Esta máscara garantiza la eficiencia del procesamiento por lotes y la causalidad de las secuencias.
Diseño de la función de pérdida
La clase CopyLoss implementa una función de pérdida para la tarea de copia.
class CopyLoss(nn.Module):
def forward(self, outputs: torch.Tensor, target: torch.Tensor,
print_details: bool = False) -> Tuple[torch.Tensor, float]:
batch_size = outputs.size(0)
predictions = F.softmax(outputs, dim=-1)
target_one_hot = F.one_hot(target, num_classes=outputs.size(-1)).float()
loss = -torch.sum(target_one_hot * torch.log(predictions + 1e-10)) / batch_size
with torch.no_grad():
pred_tokens = predictions.argmax(dim=-1)
exact_match = (pred_tokens == target).all(dim=1).float()
match_rate = exact_match.mean().item()Ejemplo de funcionamiento (batch_size=2, sequence_length=3, vocab_size=5):
# Example: batch_size=2, sequence_length=3, vocab_size=5 (example is vocab_size=20)
# 1. Model Output (logits)
outputs = [
# First batch
[[0.9, 0.1, 0.0, 0.0, 0.0], # First position: token 0 has the highest probability
[0.1, 0.8, 0.1, 0.0, 0.0], # Second position: token 1 has the highest probability
[0.0, 0.1, 0.9, 0.0, 0.0]], # Third position: token 2 has the highest probability
# Second batch
[[0.8, 0.2, 0.0, 0.0, 0.0],
[0.1, 0.7, 0.2, 0.0, 0.0],
[0.1, 0.1, 0.8, 0.0, 0.0]]
]# 2. Actual Target
target = [
[0, 1, 2], # Correct sequence for the first batch
[0, 1, 2] # Correct sequence for the second batch
]predictions = softmax(outputs) (ya convertido a probabilidades anteriormente)target a vector one-hot# 3. Loss Calculation Process
# predictions = softmax(outputs) (already converted to probabilities above)
# Convert target to one-hot vectors:
target_one_hot = [
[[1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0]], # First batch
[[1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0]] # Second batch
]# 4. Accuracy Calculation
pred_tokens = [
[0, 1, 2], # First batch prediction
[0, 1, 2] # Second batch prediction
]exact_match = [True, True] (ambos lotes son exactos)match_rate = 1.0 (100%)# Exact sequence match
exact_match = [True, True] # Both batches match exactly
match_rate = 1.0 # Average accuracy 100%
# The final loss value is the average of the cross-entropy
# loss = -1/2 * (log(0.9) + log(0.8) + log(0.9) + log(0.8) + log(0.7) + log(0.8))Visualización de atención
A través de la visualización de atención, se puede entender de manera intuitiva el funcionamiento del transformador.
from dldna.chapter_08.transformer.examples.copy_task import visualize_attention
visualize_attention(seq_length=20)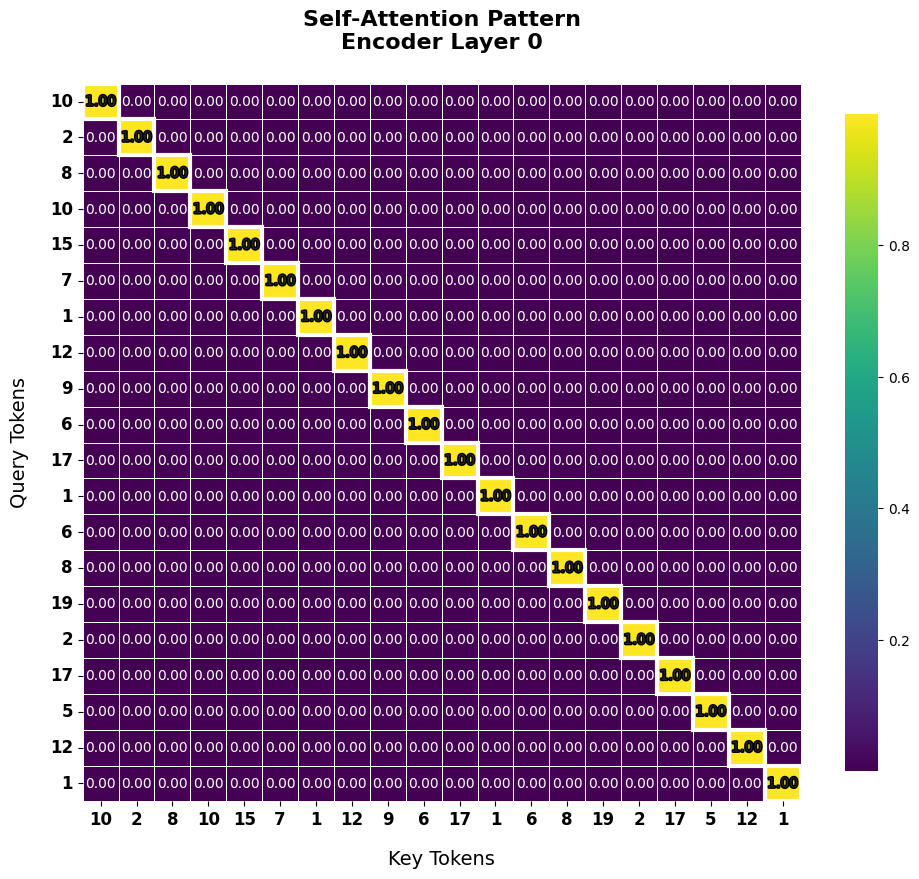
Verifica cómo cada token de entrada interactúa con tokens en otras posiciones.
A través de este ejemplo de tarea de copia, hemos examinado el mecanismo central del transformer. En el siguiente ejemplo (problema de adición), veremos cómo el transformer aprende reglas aritméticas, como las relaciones entre números y el acarreo.
El segundo ejemplo es una tarea de suma que involucra dos números. Esta tarea es adecuada para comprender la capacidad generativa autoregresiva del transformer y el proceso de cálculo secuencial del decodificador. A través del cálculo con acarreo, se puede observar cómo el transformer aprende las relaciones entre los números.
Preparación de datos
Los datos para la tarea de suma se generan en create_addition_data().
def create_addition_data(batch_size: int = 32, max_digits: int = 3) -> Tuple[torch.Tensor, torch.Tensor]:
"""Create addition dataset"""
max_value = 10 ** max_digits - 1
num1 = torch.randint(0, max_value // 2 + 1, (batch_size,))
num2 = torch.randint(0, max_value // 2 + 1, (batch_size,))
result = num1 + num2
[See source below]Descripción de los datos de entrenamiento
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.addition_task import explain_addition_data
explain_addition_data()
=== Addition Data Explanation ====
Maximum Digits: 3
1. Input Sequence:
Original Tensor Shape: torch.Size([1, 7])
First Number: 153 (Indices [np.int64(1), np.int64(5), np.int64(3)])
Plus Sign: '+' (Index 10)
Second Number: 391 (Indices [np.int64(3), np.int64(9), np.int64(1)])
Full Input: [1, 5, 3, 10, 3, 9, 1]
2. Target Sequence:
Original Tensor Shape: torch.Size([1, 3])
Actual Sum: 544
Target Sequence: [5, 4, 4]Entrenamiento y prueba del modelo
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.addition_task import train_addition_task
config = TransformerConfig()
config.vocab_size = 11
config.hidden_size = 256
config.num_hidden_layers = 3
config.num_attention_heads = 4
config.intermediate_size = 512
config.max_position_embeddings = 10
model = train_addition_task(config, num_epochs=10, batch_size=128, steps_per_epoch=300, max_digits=3)Epoch 0, Average Loss: 6.1352, Final Accuracy: 0.0073, Learning Rate: 0.000100
Epoch 5, Average Loss: 0.0552, Final Accuracy: 0.9852, Learning Rate: 0.000100
=== Loss Calculation Details (Step: 3000) ===
Predicted Sequences (First 10): tensor([[6, 5, 4],
[5, 3, 3],
[1, 7, 5],
[6, 0, 6],
[7, 5, 9],
[5, 2, 8],
[2, 8, 1],
[3, 5, 8],
[0, 7, 1],
[6, 2, 1]], device='cuda:0')
Actual Target Sequences (First 10): tensor([[6, 5, 4],
[5, 3, 3],
[1, 7, 5],
[6, 0, 6],
[7, 5, 9],
[5, 2, 8],
[2, 8, 1],
[3, 5, 8],
[0, 7, 1],
[6, 2, 1]], device='cuda:0')
Exact Match per Sequence (First 10): tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.], device='cuda:0')
Calculated Loss: 0.0106
Calculated Accuracy: 1.0000
========================================
Model saved to saved_models/transformer_addition_task.pthCuando se complete el aprendizaje, cargue el modelo almacenado y realice las pruebas.
from dldna.chapter_08.transformer.examples.addition_task import test_addition
test_addition(max_digits=3)
Addition Test (Digits: 3):
310 + 98 = 408 (Actual Answer: 408)
Correct: TrueConfiguración del modelo
La configuración del transformer para la tarea de adición es la siguiente.
config = TransformerConfig()
config.vocab_size = 11 # 0-9 digits + '+' symbol
config.hidden_size = 256 # Larger hidden dimension than copy task (sufficient capacity for learning arithmetic operations)
config.num_hidden_layers = 3 # Deeper layers (hierarchical feature extraction for handling carry operations)
config.num_attention_heads = 4 # Increased number of heads (learning relationships between different digit positions)
config.intermediate_size = 512 # FFN dimension: should be larger than hidden_size.Implementación de enmascaramiento
En la tarea de adición, la máscara de relleno es esencial. Dado que los dígitos de los números de entrada pueden variar, es necesario ignorar las posiciones de relleno para realizar cálculos precisos.
def _number_to_digits(number: torch.Tensor, max_digits: int) -> torch.Tensor:
"""숫자를 자릿수 시퀀스로 변환하며 패딩 적용"""
return torch.tensor([[int(d) for d in str(n.item()).zfill(max_digits)]
for n in number])El funcionamiento de este método es específicamente como sigue.
number = torch.tensor([7, 25, 348])
max_digits = 3
result = _number_to_digits(number, max_digits)
# 입력: [7, 25, 348]
# 과정:
# 7 -> "7" -> "007" -> [0,0,7]
# 25 -> "25" -> "025" -> [0,2,5]
# 348 -> "348" -> "348" -> [3,4,8]
# 결과: tensor([[0, 0, 7],
# [0, 2, 5],
# [3, 4, 8]])Diseño de la función de pérdida
La clase AdditionLoss implementa la función de pérdida para la tarea de suma.
class AdditionLoss(nn.Module):
def forward(self, outputs: torch.Tensor, target: torch.Tensor,
print_details: bool = False) -> Tuple[torch.Tensor, float]:
batch_size = outputs.size(0)
predictions = F.softmax(outputs, dim=-1)
target_one_hot = F.one_hot(target, num_classes=outputs.size(-1)).float()
loss = -torch.sum(target_one_hot * torch.log(predictions + 1e-10)) / batch_size
with torch.no_grad():
pred_digits = predictions.argmax(dim=-1)
exact_match = (pred_digits == target).all(dim=1).float()
match_rate = exact_match.mean().item()Ejemplo de funcionamiento de AdditionLoss (batch_size=2, sequence_length=3, vocab_size=10)
outputs = [
[[0.1, 0.8, 0.1, 0, 0, 0, 0, 0, 0, 0], # 첫 번째 자리
[0.1, 0.1, 0.7, 0.1, 0, 0, 0, 0, 0, 0], # 두 번째 자리
[0.8, 0.1, 0.1, 0, 0, 0, 0, 0, 0, 0]] # 세 번째 자리
] # 첫 번째 배치
target = [
[1, 2, 0] # 실제 정답: "120"
] # 첫 번째 배치
# 1. softmax는 이미 적용되어 있다고 가정 (outputs)
# 2. target을 원-핫 인코딩으로 변환
target_one_hot = [
[[0,1,0,0,0,0,0,0,0,0], # 1
[0,0,1,0,0,0,0,0,0,0], # 2
[1,0,0,0,0,0,0,0,0,0]] # 0
]
# 3. 손실 계산
# -log(0.8) - log(0.7) - log(0.8) = 0.223 + 0.357 + 0.223 = 0.803
loss = 0.803 / batch_size
# 4. 정확도 계산
pred_digits = [1, 2, 0] # argmax 적용
exact_match = True # 모든 자릿수가 일치
match_rate = 1.0 # 배치의 평균 정확도La salida del decodificador de transformers se transforma linealmente a vocab_size en la última capa, por lo que los logit tienen una dimensión de vocab_size.
En la siguiente sección, examinaremos cómo los transformers aprenden relaciones estructurales más complejas a través de la tarea de parsing.
El último ejemplo es una implementación de la tarea de análisis sintáctico (Parser). Esta tarea consiste en recibir expresiones matemáticas y convertirlas en árboles de análisis, lo que permite verificar cuán bien el transformer procesa información estructurada.
Explicación del proceso de preparación de datos
Los datos de entrenamiento para la tarea de análisis sintáctico se generan siguiendo los siguientes pasos:
generate_random_expression() para combinar variables (x, y, z), operadores (+, -, *, /) y números (0-9) y crear expresiones simples como “x=1+2”.parse_to_tree() para convertir las expresiones generadas en árboles de análisis de forma anidada, como ['ASSIGN', 'x', ['ADD', '1', '2']]. Este árbol representa la estructura jerárquica de la expresión.TOKEN_DICT.def create_addition_data(batch_size: int = 32, max_digits: int = 3) -> Tuple[torch.Tensor, torch.Tensor]:
"""Create addition dataset"""
max_value = 10 ** max_digits - 1
# Generate input numbers
num1 = torch.randint(0, max_value // 2 + 1, (batch_size,))
num2 = torch.randint(0, max_value // 2 + 1, (batch_size,))
result = num1 + num2
# [이하 생략]Descripción de los datos de aprendizaje Lo siguiente explica la estructura de los datos de aprendizaje. Muestra cómo cambian las expresiones y tokenización en valores.
from dldna.chapter_08.transformer.examples.parser_task import explain_parser_data
explain_parser_data()
=== Parsing Data Explanation ===
Max Tokens: 5
1. Input Sequence:
Original Tensor Shape: torch.Size([1, 5])
Expression: x = 4 + 9
Tokenized Input: [11, 1, 17, 2, 22]
2. Target Sequence:
Original Tensor Shape: torch.Size([1, 5])
Parse Tree: ['ASSIGN', 'x', 'ADD', '4', '9']
Tokenized Output: [6, 11, 7, 17, 22]Cuando se ejecuta el siguiente código, se muestran explicaciones en orden para facilitar la comprensión de cómo se estructuran los datos del ejemplo de análisis.
from dldna.chapter_08.transformer.examples.parser_task import show_parser_examples
show_parser_examples(num_examples=3 )
=== Generating 3 Parsing Examples ===
Example 1:
Generated Expression: y=7/7
Parse Tree: ['ASSIGN', 'y', ['DIV', '7', '7']]
Expression Tokens: [12, 1, 21, 5, 21]
Tree Tokens: [6, 12, 10, 21, 21]
Padded Expression Tokens: [12, 1, 21, 5, 21]
Padded Tree Tokens: [6, 12, 10, 21, 21]
Example 2:
Generated Expression: x=4/3
Parse Tree: ['ASSIGN', 'x', ['DIV', '4', '3']]
Expression Tokens: [11, 1, 18, 5, 17]
Tree Tokens: [6, 11, 10, 18, 17]
Padded Expression Tokens: [11, 1, 18, 5, 17]
Padded Tree Tokens: [6, 11, 10, 18, 17]
Example 3:
Generated Expression: x=1*4
Parse Tree: ['ASSIGN', 'x', ['MUL', '1', '4']]
Expression Tokens: [11, 1, 15, 4, 18]
Tree Tokens: [6, 11, 9, 15, 18]
Padded Expression Tokens: [11, 1, 15, 4, 18]
Padded Tree Tokens: [6, 11, 9, 15, 18]
Modelo de aprendizaje y prueba
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.parser_task import train_parser_task
config = TransformerConfig()
config.vocab_size = 25 # Adjusted to match the token dictionary size
config.hidden_size = 128
config.num_hidden_layers = 3
config.num_attention_heads = 4
config.intermediate_size = 512
config.max_position_embeddings = 10
model = train_parser_task(config, num_epochs=6, batch_size=64, steps_per_epoch=100, max_tokens=5, print_progress=True)
=== Start Training ===
Device: cuda:0
Batch Size: 64
Steps per Epoch: 100
Max Tokens: 5
Epoch 0, Average Loss: 6.3280, Final Accuracy: 0.2309, Learning Rate: 0.000100
=== Prediction Result Samples ===
Input: y = 8 * 8
Prediction: ['ASSIGN', 'y', 'MUL', '8', '8']
Truth: ['ASSIGN', 'y', 'MUL', '8', '8']
Result: Correct
Input: z = 6 / 5
Prediction: ['ASSIGN', 'z', 'DIV', '8', 'a']
Truth: ['ASSIGN', 'z', 'DIV', '6', '5']
Result: Incorrect
Epoch 5, Average Loss: 0.0030, Final Accuracy: 1.0000, Learning Rate: 0.000100
=== Prediction Result Samples ===
Input: z = 5 - 6
Prediction: ['ASSIGN', 'z', 'SUB', '5', '6']
Truth: ['ASSIGN', 'z', 'SUB', '5', '6']
Result: Correct
Input: y = 9 + 9
Prediction: ['ASSIGN', 'y', 'ADD', '9', '9']
Truth: ['ASSIGN', 'y', 'ADD', '9', '9']
Result: Correct
Model saved to saved_models/transformer_parser_task.pthRealiza la prueba.
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.parser_task import test_parser
test_parser()
=== Parser Test ===
Input Expression: x = 8 * 3
Predicted Parse Tree: ['ASSIGN', 'x', 'MUL', '8', '3']
Actual Parse Tree: ['ASSIGN', 'x', 'MUL', '8', '3']
Correct: True
=== Additional Tests ===
Input: x=1+2
Predicted Parse Tree: ['ASSIGN', 'x', 'ADD', '2', '3']
Input: y=3*4
Predicted Parse Tree: ['ASSIGN', 'y', 'MUL', '4', '5']
Input: z=5-1
Predicted Parse Tree: ['ASSIGN', 'z', 'SUB', '6', '2']
Input: x=2/3
Predicted Parse Tree: ['ASSIGN', 'x', 'DIV', '3', '4']Configuración del modelo - vocab_size: 25 (tamaño del diccionario de tokens) - hidden_size: 128 - num_hidden_layers: 3 - num_attention_heads: 4 - intermediate_size: 512 - max_position_embeddings: 10 (número máximo de tokens)
Diseño de la función de pérdida
La función de pérdida para la tarea de parsing utiliza la entropía cruzada.
Ejemplo de funcionamiento de la función de pérdida
# Example input values (batch_size=2, sequence_length=4, vocab_size=5)
# vocab = {'=':0, 'x':1, '+':2, '1':3, '2':4}
outputs = [
# First batch: prediction probabilities for "x=1+2"
[[0.1, 0.7, 0.1, 0.1, 0.0], # predicting x
[0.8, 0.1, 0.0, 0.1, 0.0], # predicting =
[0.1, 0.0, 0.1, 0.7, 0.1], # predicting 1
[0.0, 0.1, 0.8, 0.0, 0.1]], # predicting +
# Second batch: prediction probabilities for "x=2+1"
[[0.1, 0.8, 0.0, 0.1, 0.0], # predicting x
[0.7, 0.1, 0.1, 0.0, 0.1], # predicting =
[0.1, 0.0, 0.1, 0.1, 0.7], # predicting 2
[0.0, 0.0, 0.9, 0.1, 0.0]] # predicting +
]
target = [
[1, 0, 3, 2], # Actual answer: "x=1+"
[1, 0, 4, 2] # Actual answer: "x=2+"
]
# Convert target to one-hot encoding
target_one_hot = [
[[0,1,0,0,0], # x
[1,0,0,0,0], # =
[0,0,0,1,0], # 1
[0,0,1,0,0]], # +
[[0,1,0,0,0], # x
[1,0,0,0,0], # =
[0,0,0,0,1], # 2
[0,0,1,0,0]] # +
]
# Loss calculation (first batch)
# -log(0.7) - log(0.8) - log(0.7) - log(0.8) = 0.357 + 0.223 + 0.357 + 0.223 = 1.16
# Loss calculation (second batch)
# -log(0.8) - log(0.7) - log(0.7) - log(0.9) = 0.223 + 0.357 + 0.357 + 0.105 = 1.042
# Total loss
loss = (1.16 + 1.042) / 2 = 1.101
# Accuracy calculation
pred_tokens = [
[1, 0, 3, 2], # First batch prediction
[1, 0, 4, 2] # Second batch prediction
]
exact_match = [True, True] # Both batches match exactly
match_rate = 1.0 # Overall accuracyHasta ahora, a través de los ejemplos, hemos podido ver que el transformer puede procesar eficazmente la información estructural.
En el Capítulo 8, exploramos en profundidad el contexto del nacimiento del transformer y sus componentes clave. Examinamos las dificultades que los investigadores enfrentaron para superar las limitaciones de los modelos basados en RNN, el descubrimiento y desarrollo del mecanismo de atención, y cómo las ideas centrales del transformer se concretizaron gradualmente a través de la separación de espacios vectoriales Q, K, V y la atención multi-cabeza para procesamiento paralelo y captura de información contextual desde diferentes perspectivas. También analizamos en detalle la codificación posicional para representar eficazmente la información de posición, las sofisticadas estrategias de máscara para evitar fugas de información, y la estructura codificador-decodificador junto con el rol y funcionamiento de cada componente.
A través de tres ejemplos (copia simple, suma de dígitos, analizador), pudimos entender intuitivamente cómo funciona el transformer en la práctica y qué roles desempeñan sus componentes. Estos ejemplos muestran las capacidades básicas del transformer, su habilidad para generar de manera autoregresiva, y su capacidad para procesar información estructural, proporcionando una base de conocimientos para aplicar el transformer a problemas reales de procesamiento de lenguaje natural.
En el Capítulo 9, seguiremos la evolución del transformer desde la publicación del artículo “Attention is All You Need”. Examinaremos cómo surgieron modelos basados en transformers como BERT y GPT, y cómo estos modelos han llevado innovaciones más allá del procesamiento de lenguaje natural, incluyendo visión por computadora y reconocimiento de voz.
Ventajas del Transformer frente al RNN: El Transformer tiene dos grandes ventajas sobre el RNN: la procesamiento en paralelo y la resolución del problema de dependencias a largo plazo. El RNN procesa secuencialmente, lo que hace que sea lento, mientras que el Transformer utiliza atención para procesar todas las palabras simultáneamente, permitiendo cálculos paralelos en GPU y acelerando el aprendizaje. Además, el RNN sufre una pérdida de información en secuencias largas, pero el Transformer conserva la información importante independientemente de la distancia mediante la atención propia (self-attention).
Núcleo y efectos del mecanismo de atención: La atención calcula qué tan importantes son las diferentes partes de la secuencia de entrada para la generación de la secuencia de salida. El decodificador no trata todas las entradas por igual al predecir palabras de salida, sino que “presta atención” a las partes más relevantes, mejorando así su comprensión del contexto y permitiendo predicciones más precisas.
Ventajas de la atención multi-cabezal: La atención multi-cabezal realiza múltiples operaciones de autoatención en paralelo. Cada cabeza aprende las relaciones entre palabras dentro de la secuencia desde perspectivas diferentes, lo que ayuda al modelo a capturar información contextual más rica y diversa. (Similar a cómo varios detectives colaboran con sus propias áreas de especialización)
Necesidad y método de codificación posicional: Dado que el Transformer no procesa secuencias en orden, es necesario proporcionarle la información sobre la posición de las palabras. La codificación posicional funciona agregando un vector con información de posición a cada embedding de palabra. De esta manera, el Transformer puede considerar tanto el significado como la ubicación de las palabras dentro de una oración para comprender el contexto. Se utilizan principalmente funciones seno-coseno para representar la información de posición.
Roles del codificador y decodificador: El Transformer utiliza una estructura de codificador-decodificador. El codificador toma la secuencia de entrada y genera representaciones (vectores contextuales) que reflejan el contexto de cada palabra. El decodificador repite el proceso de predecir la siguiente palabra basándose en los vectores contextuales generados por el codificador y las palabras de salida generadas en pasos anteriores, hasta generar la secuencia de salida final.
Análisis comparativo de métodos para mejorar la complejidad computacional:
El transformador tiene una complejidad computacional cuadrática con respecto a la longitud de la secuencia de entrada debido a la atención propia. Se han propuesto varios métodos para mejorar esto.
Propuesta y evaluación de nuevas arquitecturas:
Análisis e iniciativas de respuesta a impactos éticos y sociales: El desarrollo de grandes modelos de lenguaje basados en transformers (por ejemplo, GPT-3, BERT) puede tener diversos impactos positivos y negativos en la sociedad.