Code
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local 
3. Deep Learning Frameworks
“Das Werkzeug ist so gut wie der, der es macht.” - anonym, aber oft Jacques Hadamard zugeschrieben
Die Entwicklung von Frameworks in der Geschichte des Deep Learnings war sehr wichtig. Nach dem Erfolg von AlexNet im Jahr 2012 erschienen verschiedene Frameworks. Durch Caffe, Theano und Torch7 sind wir heute bei PyTorch und TensorFlow angelangt.
Anfang der 2010er Jahre begann das Deep Learning in verschiedenen Bereichen wie Bilderkennung und Spracherkennung beeindruckende Ergebnisse zu erzielen, die die bestehenden Technologien übertrafen. Trotzdem war es immer noch schwierig, Deep-Learning-Modelle zu trainieren und bereitzustellen. Dies lag daran, dass Neuronale Netze aufbauen, Gradienten berechnen und GPU-Beschleunigung direkt implementiert werden mussten. Diese Komplexität erhöhte den Einstiegsschwelle für Deep-Learning-Forschung und verlangsamte die Forschungsfortschritte. Um diese Probleme zu lösen, erschienen Deep-Learning-Frameworks. Sie vereinfachten und beschleunigten den Entwicklungsprozess durch hochwertige APIs und Tools zur Erstellung, Trainierung und Bereitstellung von Neuronalen Netzmodellen. In der Frühphase wurden Frameworks wie Theano, Caffe und Torch in Wissenschaft und Industrie weit verbreitet genutzt.
2015 veröffentlichte Google TensorFlow als Open-Source-Projekt und brachte damit eine große Veränderung im Ökosystem der Deep-Learning-Frameworks. TensorFlow gewann schnell an Popularität dank seiner flexiblen Architektur, starker Visualisierungstools und Unterstützung für großskaliges verteiltes Lernen. 2017 stellte Facebook PyTorch vor und setzte damit ein weiteres wichtiges Meilenstein. PyTorch gewann schnell an Beliebtheit unter Forschern dank dynamischer Berechnungsgraphen, intuitiver Schnittstellen und hervorragender Debugging-Funktionen.
Heutzutage sind Deep-Learning-Frameworks weit mehr als einfach nur Werkzeuge; sie sind ein zentrales Infrastrukturelement der Deep-Learning-Forschung und -Entwicklung. Sie bieten Kernfunktionen wie automatische Differentiation, GPU-Beschleunigung, Modell-Parallelisierung und verteiltes Lernen, beschleunigen die Entwicklung neuer Modelle und Algorithmen. Darüber hinaus fördern der Wettbewerb und die Zusammenarbeit zwischen den Frameworks die weitere Entwicklung des Deep-Learning-Ökosystems.
3.1 PyTorch
PyTorch ist ein Open-Source-Maschinelles Lernalgorithmus-Framework, das auf der Torch-Bibliothek basiert und in Anwendungen wie Computer Vision und Natural Language Processing eingesetzt wird. Es wurde 2016 von Facebook’s AI Research Lab (FAIR) als Kernframework entwickelt, indem es Torch7 in Python neu implementierte. Dank dynamischer Berechnungsgraphen und intuitiver Debugging-Funktionen gewann PyTorch schnell an Beliebtheit unter Forschern. Obwohl andere Frameworks wie TensorFlow, JAX und Caffe existieren, ist PyTorch zum de facto-Standard in der Forschung geworden. Viele neue Modelle werden häufig zusammen mit einer PyTorch-Implementierung veröffentlicht.
Nachdem man sich auf ein Framework spezialisiert hat, kann es eine gute Strategie sein, die Stärken anderer Frameworks zu nutzen. Zum Beispiel können TensorFlow-Datenvorverarbeitungs-Pipelines oder funktionale Transformationen in JAX mit PyTorch kombiniert werden.
Code
import torch
# Print PyTorch version
print(f"PyTorch version: {torch.__version__}")
# Set the random seed for reproducibility
torch.manual_seed(7)PyTorch version: 2.6.0+cu124<torch._C.Generator at 0x7352f02b33f0>Wenn man beim Erzeugen von Zufallszahlen einen anfänglichen Seed-Wert festlegt, kann man immer die gleichen Zufallszahlen erhalten. Dies wird häufig in der Forschung verwendet, um konsistente Ergebnisse bei wiederholten Trainingsläufen zu gewährleisten.
3.1.1 Tensor-Objekt
Herausforderung: Wie können große Matrixoperationen effizient mit GPU durchgeführt werden?
Forscherleid: Mit der Vergrößerung der Größe von Deep-Learning-Modellen dauerte das Training und die Inferenz mit CPU allein viel zu lange. GPU war auf parallele Berechnungen spezialisiert und für Deep Learning geeignet, aber GPU-Programmierung war komplex und schwierig. Es war ein Tool erforderlich, um GPU-Berechnungen abstrahiert und automatisiert zu gestalten, damit Deep-Learning-Forscher die GPU leichter nutzen können.
Ein Tensor ist die grundlegende Datenstruktur von PyTorch. Nachdem CUDA 2006 erschien, wurde GPU-Rechnung zum Kern von Deep Learning, und Tensoren wurden so entworfen, dass sie diese GPU-Berechnungen effizient durchführen können. Ein Tensor ist ein mehrdimensionales Array, das Skalare, Vektoren und Matrizen verallgemeinert. In Deep Learning sind die Dimensionen der Daten (Tensorrang) sehr vielfältig. Zum Beispiel wird ein Bild als 4-dimensionaler Tensor mit den Dimensionen (Batch, Kanäle, Höhe, Breite) und natürliche Sprache als 3-dimensionaler Tensor mit den Dimensionen (Batch, Sequenzlänge, Embedding-Dimension) dargestellt. Wie in Kapitel 2 gezeigt, ist es wichtig, diese Dimensionen frei zu verformen und zu verarbeiten.
Ein Tensor kann wie folgt deklariert werden.
Code
import numpy as np
import torch
# Create a 3x2x4 tensor with random values
a = torch.Tensor(3, 2, 4)
print(a)tensor([[[ 1.1210e-44, 0.0000e+00, 0.0000e+00, 4.1369e-41],
[ 1.8796e-17, 0.0000e+00, 2.8026e-45, 0.0000e+00]],
[[ 0.0000e+00, 0.0000e+00, nan, nan],
[ 6.3058e-44, 4.7424e+30, 1.4013e-45, 1.3563e-19]],
[[ 1.0089e-43, 0.0000e+00, 1.1210e-44, 0.0000e+00],
[-8.8105e+09, 4.1369e-41, 1.8796e-17, 0.0000e+00]]])Von vorhandenen Daten kann man auch Tensoren initialisieren.
Code
# From a Python list
d = [[1, 2], [3, 4]]
print(f"Type of d: {type(d)}")
a = torch.Tensor(d) # Creates a *copy*
print(f"Tensor a:\n{a}")
print(f"Type of a: {type(a)}")
# From a NumPy array
d_np = np.array(d)
print(f"Type of d_np: {type(d_np)}")
b = torch.from_numpy(d_np) # Shares memory with d_np (zero-copy)
print(f"Tensor b (from_numpy):\n{b}")
c = torch.Tensor(d_np) # Creates a *copy*
print(f"Tensor c (from np array using torch.Tensor):\n{c}")
# Example of memory sharing with torch.from_numpy
d_np[0, 0] = 100
print(f"Modified d_np:\n{d_np}")
print(f"Tensor b (from_numpy) after modifying d_np:\n{b}")
print(f"Tensor c (copy) after modifying d_np:\n{c}")Type of d: <class 'list'>
Tensor a:
tensor([[1., 2.],
[3., 4.]])
Type of a: <class 'torch.Tensor'>
Type of d_np: <class 'numpy.ndarray'>
Tensor b (from_numpy):
tensor([[1, 2],
[3, 4]])
Tensor c (from np array using torch.Tensor):
tensor([[1., 2.],
[3., 4.]])
Modified d_np:
[[100 2]
[ 3 4]]
Tensor b (from_numpy) after modifying d_np:
tensor([[100, 2],
[ 3, 4]])
Tensor c (copy) after modifying d_np:
tensor([[1., 2.],
[3., 4.]])Die Tatsache, dass sie beim Ausgeben gleich aussehen, bedeutet nicht, dass es sich um dieselben Objekte handelt. d ist ein Python-List-Objekt und Tensoren können aus verschiedenen Datenstrukturen erstellt werden. Insbesondere sind die Wechselwirkungen mit NumPy-Arrays sehr effizient. Allerdings unterstützen Listenobjekte und NumPy-Arrays keine GPU, daher ist eine Konvertierung in Tensoren für große Berechnungen unerlässlich. Ein wichtiger Punkt ist das Verständnis der Unterschiede zwischen torch.Tensor(data) und torch.from_numpy(data). Der Erstere erstellt immer eine Kopie, während Letzterer einen View erstellt, der die Speicheradresse des ursprünglichen NumPy-Arrays teilt (bei möglichem - Null-Kopie). Änderungen am NumPy-Array führen zu Änderungen im mit from_numpy erstellten Tensor und umgekehrt.
Es gibt viele Möglichkeiten, Tensoren zu initialisieren. Seit Hintons Papier von 2006 wurde die Bedeutung der Initialisierung hervorgehoben und verschiedene Initialisierungsstrategien wurden entwickelt. Die grundlegendsten Initialisierungsfunktionen sind wie folgt:
torch.zeros: Initialisiert mit 0.torch.ones: Initialisiert mit 1.torch.rand: Initialisiert mit Zufallszahlen aus einer Gleichverteilung zwischen 0 und 1.torch.randn: Initialisiert mit Zufallszahlen aus einer Standardnormalverteilung (Mittelwert 0, Varianz 1).torch.arange: Initialisiert in aufsteigender Reihenfolge wie n, n+1, n+2, …
Code
shape = (2, 3)
rand_t = torch.rand(shape) # Uniform distribution [0, 1)
randn_t = torch.randn(shape) # Standard normal distribution
ones_t = torch.ones(shape)
zeros_t = torch.zeros(shape)
print(f"Random tensor (uniform):\n{rand_t}")
print(f"Random tensor (normal):\n{randn_t}")
print(f"Ones tensor:\n{ones_t}")
print(f"Zeros tensor:\n{zeros_t}")Random tensor (uniform):
tensor([[0.5349, 0.1988, 0.6592],
[0.6569, 0.2328, 0.4251]])
Random tensor (normal):
tensor([[-1.2514, -1.8841, 0.4457],
[-0.7068, -1.5750, -0.6318]])
Ones tensor:
tensor([[1., 1., 1.],
[1., 1., 1.]])
Zeros tensor:
tensor([[0., 0., 0.],
[0., 0., 0.]])PyTorch unterstützt über 100 Tensor-Operationen, und alle können auf der GPU ausgeführt werden. Tensoren werden standardmäßig im CPU-Speicher erstellt, daher müssen sie mit der to()-Funktion explizit auf die GPU verschoben werden, um diese zu verwenden. Das Verschieben großer Tensoren zwischen CPU und GPU kann erhebliche Kosten verursachen, weshalb eine sorgfältige Speicherverwaltung unerlässlich ist. In der praktischen Deep-Learning-Trainierung hat die Speicherbandbreite der GPU einen entscheidenden Einfluss auf die Leistung. Zum Beispiel kann bei der Training von Transformer-Modellen eine größere GPU-Speichergröße den Einsatz größerer Batchgrößen ermöglichen, was die Trainings-effizienz erhöht. Allerdings ist hohe Bandbreite sehr teuer herzustellen und macht einen großen Teil des GPU-Preises aus. Die Leistungsunterschiede zwischen CPU- und GPU-Tensoroperationen sind besonders bei parallelisierbaren Operationen wie Matrix-Multiplikationen auffällig. Aus diesen Gründen sind in der modernen Deep-Learning-Szene spezialisierte Beschleuniger wie GPUs, TPUs, NPUs unerlässlich.
Code
# Device setting
if torch.cuda.is_available():
tensor = zeros_t.to("cuda")
device = "cuda:0"
else:
device = "cpu"
print('GPU not available')
# CPU/GPU performance comparison
import time
# CPU operation
x = torch.rand(10000, 10000)
start = time.time()
torch.matmul(x, x)
cpu_time = time.time() - start
print(f"CPU computation time = {cpu_time:3.2f} seconds")
# GPU operation
if device != "cpu":
x = x.to(device)
start = torch.cuda.Event(enable_timing=True)
end = torch.cuda.Event(enable_timing=True)
start.record()
torch.matmul(x, x)
end.record()
torch.cuda.synchronize() # Wait for all operations to complete
gpu_time = start.elapsed_time(end) / 1000 # Convert milliseconds to seconds
print(f"GPU computation time = {gpu_time:3.2f} seconds")
print(f"GPU is {cpu_time / gpu_time:3.1f} times faster.")CPU computation time = 2.34 seconds
GPU computation time = 0.14 seconds
GPU is 16.2 times faster.Die Konvertierung zwischen NumPy und Tensoren ist sehr effizient implementiert. Insbesondere, wie oben gezeigt, wird mit torch.from_numpy() der Speicher ohne Kopieren geteilt.
Code
np_a = np.array([[1, 1], [2, 3]])
tensor_a = torch.from_numpy(np_a)
np_b = tensor_a.numpy() # Shares memory. If tensor_a is on CPU.
print(f"NumPy array: {np_a}")
print(f"Tensor: {tensor_a}")
print(f"NumPy array from Tensor: {np_b}") #if tensor_a is on CPU.NumPy array: [[1 1]
[2 3]]
Tensor: tensor([[1, 1],
[2, 3]])
NumPy array from Tensor: [[1 1]
[2 3]]Beim Konvertieren von Tensoren in NumPy müssen die Tensoren unbedingt auf dem CPU sein. Tensoren auf dem GPU müssen zunächst mit .cpu() auf den CPU verschoben werden. Die grundlegenden Eigenschaften eines Tensors sind shape, dtype und device, über die die Form und den Speicherort des Tensors ermittelt werden können.
Code
a = torch.rand(2, 3)
print(f"Shape = {a.shape}")
print(f"Data type = {a.dtype}")
print(f"Device = {a.device}")Shape = torch.Size([2, 3])
Data type = torch.float32
Device = cpuIndizierung und Slicing verwenden die gleiche Syntax wie NumPy.
Code
a = torch.rand(3, 3)
print(f"Tensor a:\n{a}")
print(f"First row: {a[0]}")
print(f"First column: {a[:, 0]}")
print(f"Last column: {a[..., -1]}") # Equivalent to a[:, -1]Tensor a:
tensor([[0.2069, 0.8296, 0.4973],
[0.9265, 0.8386, 0.6611],
[0.5329, 0.7822, 0.0975]])
First row: tensor([0.2069, 0.8296, 0.4973])
First column: tensor([0.2069, 0.9265, 0.5329])
Last column: tensor([0.4973, 0.6611, 0.0975])3.1.2 Operationen
PyTorch unterstützt fast alle Operationen von NumPy. Die Tradition der Operationen mit mehrdimensionalen Arrays, die 1964 mit der APL-Sprache begann, wurde über NumPy bis hin zu PyTorch fortgeführt. Eine Liste aller unterstützten Operationen können Sie in der offiziellen PyTorch-Dokumentation (PyTorch Dokumentation) finden.
Die Formänderung von Tensoren ist eine der häufigsten Operationen in neuronalen Netzen. Mit der view()-Funktion können die Dimensionen eines Tensors geändert werden, wobei die Gesamtanzahl der Elemente beibehalten werden muss. Die permute()-Funktion ordnet die Reihenfolge der Dimensionen neu.
Code
a = torch.arange(12)
print(f"a: {a}")
x = a.view(3, 4) # Reshape to 3x4
print(f"x: {x}")
y = x.permute(1, 0) # Swap dimensions 0 and 1
print(f"y: {y}")
b = torch.randn(2, 3, 5)
print(f"b shape: {b.shape}")
z = b.permute(2, 0, 1) # Change dimension order to (2, 0, 1)
print(f"z shape: {z.shape}")a: tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
x: tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
y: tensor([[ 0, 4, 8],
[ 1, 5, 9],
[ 2, 6, 10],
[ 3, 7, 11]])
b shape: torch.Size([2, 3, 5])
z shape: torch.Size([5, 2, 3])Matrix-Operationen sind der Kern von Deep Learning, und PyTorch bietet verschiedene Funktionen für Matrix-Operationen.
torch.matmul: Führt allgemeine Matrix-Operationen durch. Das Verhalten hängt von den Dimensionen ab:- 1D × 1D: Skalarprodukt (dot product)
- 2D × 2D: Matrixmultiplikation
- 1D × 2D: Eine zusätzliche Dimension wird dem ersten Tensor hinzugefügt, bevor die Matrixmultiplikation durchgeführt wird.
- N-D × M-D: Nach Broadcasting wird die Matrixmultiplikation durchgeführt.
torch.mm: Reine Matrixmultiplikation (kein Broadcasting)torch.bmm: Matrixmultiplikation mit Batch-Dimension ((b, i, k) × (b, k, j) → (b, i, j))torch.einsum: Tensor-Operationen mit Einsteins Summenkonvention. Komplexe Tensor-Operationen können kompakt ausgedrückt werden. (Weitere Details siehe “Theoretisches Deep Dive”)torch.einsum('ij,jk->ik', a, b): Produkt der Matrizen a und b
Code
a = torch.arange(6)
b = torch.arange(12)
X = a.view(2, 3)
Y = b.view(3, 4)
print(f"X: {X}")
print(f"Y: {Y}")
# matmul (2,3) X (3,4) -> (2, 4)
print(f"X @ Y = {torch.matmul(X, Y)}")
# Using torch.einsum for matrix multiplication
einsum_result = torch.einsum('ij,jk->ik', X, Y)
print(f"X @ Y (using einsum) = {einsum_result}")
a = torch.arange(2)
b = torch.arange(2)
print(f"a: {a}")
print(f"b: {b}")
# Vector x Vector operation
print(f"a @ b = {torch.matmul(a, b)}")
# 1D tensor (vector), 2D tensor (matrix) operation
# (2) x (2,2) is treated as (1,2) x (2,2) for matrix multiplication.
# Result: (1,2) x (2,2) -> (1,2)
b = torch.arange(4)
B = b.view(2, 2)
print(f"a: {a}")
print(f"B: {B}")
print(f"a @ B = {torch.matmul(a, B)}")
# Matrix x Vector operation
X = torch.randn(3, 4)
b = torch.randn(4)
print(f"X @ b shape = {torch.matmul(X, b).size()}")
# Batched matrix x Batched matrix
# The leading batch dimension is maintained.
# The 2nd and 3rd dimensions are treated as matrices for multiplication.
X = torch.arange(18).view(3, 2, 3)
Y = torch.arange(18).view(3, 3, 2)
print(f"X: {X}")
print(f"Y: {Y}")
# Batch dimension remains the same, and (2,3)x(3,2) -> (2,2)
print(f"X @ Y shape: {torch.matmul(X, Y).size()}")
print(f"X @ Y: {torch.matmul(X, Y)}")
# Batched matrix x Broadcasted matrix
X = torch.arange(18).view(3, 2, 3)
Y = torch.arange(6).view(3, 2)
print(f"X: {X}")
print(f"Y: {Y}")
# The second matrix lacks a batch dimension.
# It's broadcasted to match the batch dimension of the first matrix (repeated 3 times).
print(f"X @ Y shape: {torch.matmul(X, Y).size()}")
print(f"X @ Y: {torch.matmul(X, Y)}")
# Using torch.einsum for matrix multiplication
X = torch.arange(6).view(2, 3)
Y = torch.arange(12).view(3, 4)
einsum_result = torch.einsum('ij,jk->ik', X, Y) # Equivalent to torch.matmul(X, Y)
print(f"X @ Y (using einsum) = {einsum_result}")X: tensor([[0, 1, 2],
[3, 4, 5]])
Y: tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
X @ Y = tensor([[20, 23, 26, 29],
[56, 68, 80, 92]])
X @ Y (using einsum) = tensor([[20, 23, 26, 29],
[56, 68, 80, 92]])
a: tensor([0, 1])
b: tensor([0, 1])
a @ b = 1
a: tensor([0, 1])
B: tensor([[0, 1],
[2, 3]])
a @ B = tensor([2, 3])
X @ b shape = torch.Size([3])
X: tensor([[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]],
[[12, 13, 14],
[15, 16, 17]]])
Y: tensor([[[ 0, 1],
[ 2, 3],
[ 4, 5]],
[[ 6, 7],
[ 8, 9],
[10, 11]],
[[12, 13],
[14, 15],
[16, 17]]])
X @ Y shape: torch.Size([3, 2, 2])
X @ Y: tensor([[[ 10, 13],
[ 28, 40]],
[[172, 193],
[244, 274]],
[[550, 589],
[676, 724]]])
X: tensor([[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]],
[[12, 13, 14],
[15, 16, 17]]])
Y: tensor([[0, 1],
[2, 3],
[4, 5]])
X @ Y shape: torch.Size([3, 2, 2])
X @ Y: tensor([[[ 10, 13],
[ 28, 40]],
[[ 46, 67],
[ 64, 94]],
[[ 82, 121],
[100, 148]]])
X @ Y (using einsum) = tensor([[20, 23, 26, 29],
[56, 68, 80, 92]])torch.einsum verwendet die Einstein-Notation, um Tensoroperationen darzustellen. 'ij,jk->ik' bedeutet, dass die Dimensionen (i, j) des Tensors X und die Dimensionen (j, k) des Tensors Y multipliziert werden, um ein Ergebnis mit den Dimensionen (i, k) zu erzeugen. Dies entspricht dem Matrizenprodukt torch.matmul(X, Y). einsum unterstützt neben diesem auch Transposition, Summation, Skalarprodukt, dyadisches Produkt und Batch-Matrizenmultiplikation sowie viele andere Operationen. Weitere Informationen finden Sie in der PyTorch-Dokumentation.
Code
# Other einsum examples
# Transpose
a = torch.randn(2, 3)
b = torch.einsum('ij->ji', a) # Swap dimensions
# Sum of all elements
a = torch.randn(2, 3)
b = torch.einsum('ij->', a) # Sum all elements
# Batch matrix multiplication
a = torch.randn(3, 2, 5)
b = torch.randn(3, 5, 3)
c = torch.einsum('bij,bjk->bik', a, b) # Batch matrix multiplication
Klicken Sie hier, um den Inhalt anzuzeigen (Tiefenaufnahme: Einstein-Notation und torch.einsum)
Einsteinsche Notation und torch.einsum
Einsteinsche Notation (Einstein Notation)
Die Einsteinsche Notation (auch Einstein Summationskonvention genannt) wurde 1916 von Albert Einstein eingeführt, um die allgemeine Relativitätstheorie zu beschreiben. Ursprünglich entwickelt, um physikalische Formeln, insbesondere der Relativitätstheorie, kompakt darzustellen, wird sie heute dank ihrer Handhabungsfreundlichkeit und Ausdrucksstärke in verschiedenen Bereichen zur Behandlung von Tensoroperationen häufig verwendet.
Kerngedanke:
- Wiederkehrende Indizes bedeuten Summation: Wenn ein Index in einem Term zweimal auftritt, impliziert dies, dass über diesen Index alle möglichen Werte summiert werden. Das explizite Summenzeichen (\(\\sum\)) wird weggelassen, um die Notation zu verkürzen.
- Freie Indizes und Dummy-Indizes:
- Freier Index (free index): Ein Index, der im Ergebnistensor auftritt. Er erscheint in jedem Term nur einmal.
- Dummy-Index (dummy index): Ein Index, über den summiert wird. Er erscheint in einem Term zweimal. (Summationsindex, gebundener Index)
Grundregeln
- Wenn ein Index in einem Term zweimal auftritt, wird über diesen Index summiert.
- Freie Indizes bestimmen die Dimensionen des Ergebnistensors.
- Dummy-Indizes werden nur für interne Berechnungen verwendet und erscheinen nicht im Ergebnis.
- Indexbuchstaben können beliebig gewählt werden, aber um Verwirrung zu vermeiden, sollte man konsistent bleiben. (Üblicherweise werden \(i, j, k, l, m, n\) usw. verwendet)
- Der Pfeil (\(\\rightarrow\)) links steht für den Eingabetensor, rechts für den Ausgabetensor.
Beispiele
- Skalarprodukt (dot product): \(a\_i b\_i\) (entspricht \(\\sum\_i a\_i b\_i\))
- Matrixmultiplikation (matrix multiplication): \(A\_{ij} B\_{jk} = C\_{ik}\) (entspricht \(\\sum\_j A\_{ij}B\_{jk\)})
- Transposition (transpose): \(A\_{ij} = B\_{ji}\) (B ist die transponierte Matrix von A)
- Spur (trace): \(A\_{ii}\) (entspricht \(\\sum\_i A\_{ii\))
- Kreuzprodukt (outer product): \(a\_i b\_j = C\_{ij}\)
- Elementweise Multiplikation (element-wise multiplication): \(A\_{ij}B\_{ij} = C\_{ij}\) (Hadamard-Produkt)
Anwendungsbeispiele in Deep Learning
Einsteinsche Notation und torch.einsum * Batched Matrix Multiplikation: \(A\_{bij} B\_{bjk} = C\_{bik}\) (\(b\): Batch-Dimension) * Aufmerksamkeitsmechanismus (Attention Mechanism): \(e\_{ij} = Q\_{ik} K\_{jk}\), \(a\_{ij} = \text{softmax}(e\_{ij})\), \(v\_{i} = a\_{ij} V\_{j}\) (\(Q\): Query, \(K\): Key, \(V\): Value) * Bilineare Transformation: \(x\_i W\_{ijk} y\_j = z\_k\) * Mehrdimensionale Faltung (Convolution): \(I\_{b,c,i,j} \* F\_{o,c,k,l} = O\_{b,o,i',j'}\) (\(b\): Batch, \(c\): Eingangskanäle, \(o\): Ausgangskanäle, \(i, j\): Eingangsraumdimensionen, \(k, l\): Filterraumdimensionen) * Batch Normalisierung: \(\gamma\_c \* \frac{x\_{b,c,h,w} - \mu\_c}{\sigma\_c} + \beta\_c\) (\(c\): Kanal-Dimension, \(b\): Batch, \(h\): Höhe, \(w\): Breite) * RNN Hidden State Update: \(h\_t = \tanh(W\_{ih}x\_t + b\_{ih} + W\_{hh}h\_{t-1} + b\_{hh})\) (\(h\): hidden, \(x\): input, \(W\): Gewicht, \(b\): Bias) * LSTM Cell State Update: \(c\_t = f\_t \* c\_{t-1} + i\_t \* \tilde{c}\_t\) (\(c\): Cell State, \(f\): Forget Gate, \(i\): Input Gate, \(\tilde{c}\_t\): Kandidat-Cell-State)
torch.einsum
torch.einsum ist eine Funktion in PyTorch, die Einstein-Summenkonvention verwendet, um Tensoroperationen durchzuführen. einsum steht für “Einstein summation”.
Verwendung:
torch.einsum(equation, *operands)equation: Zeichenkette in Einstein-Summennotation, wie'ij,jk->ik'.*operands: die an der Operation beteiligten Tensoren (variabler Parameter).
Vorteile
- Kürze: Komplexe Tensoroperationen können mit einer Codezeile ausgedrückt werden.
- Lesbarkeit: Einstein-Summennotation macht den Sinn von Tensoroperationen klar.
- Flexibilität: Verschiedene Tensoroperationen können kombiniert werden, um neue Operationen leicht zu definieren.
- Optimierung: PyTorch optimiert
einsum-Operationen automatisch für eine effiziente Berechnung. (In bestimmten Fällen) kann dies schneller sein als manuell implementierte Operationen. Es nutzt optimierte Routinen von Bibliotheken wie BLAS, cuBLAS oder optimiert die Reihenfolge der Operationen. - Unterstützung für automatisches Differenzieren:
einsum-definierte Operationen sind vollständig mit PyTorchs System zur automatischen Ableitung kompatibel.
torch.einsum Beispiel:
import torch
# Matrixmultiplikation
A = torch.randn(3, 4)
B = torch.randn(4, 5)
C = torch.einsum('ij,jk->ik', A, B) # C = A @ B
# Transposition
A = torch.randn(3, 4)
B = torch.einsum('ij->ji', A) # B = A.T
# Spur (Trace)
A = torch.randn(3, 3)
trace = torch.einsum('ii->', A) # trace = torch.trace(A)Batch-Matrix-Multiplikation
A = torch.randn(2, 3, 4) B = torch.randn(2, 4, 5) C = torch.einsum(‘bij,bjk->bik’, A, B) # C = torch.bmm(A, B)
Äußeres Produkt
a = torch.randn(3) b = torch.randn(4) C = torch.einsum(‘i,j->ij’, a, b) # C = torch.outer(a, b)
Elementweises Produkt
A = torch.randn(2,3) B = torch.randn(2,3) C = torch.einsum(‘ij,ij->ij’, A, B) # C = A * B
Bilineare Transformation
x = torch.randn(3) W = torch.randn(5, 3, 4) y = torch.randn(4) z = torch.einsum(‘i,ijk,j->k’, x, W, y) # z_k = sum_i sum_j x_i * W_{ijk} * y_j
Reduktion von Mehrdimensionalen Tensoren
tensor = torch.randn(3, 4, 5, 6) result = torch.einsum(‘…ij->…i’, tensor) # Letzte beiden Dimensionen zusammenfassen
**`torch.einsum` vs. andere Operationen:**
| Operation | `torch.einsum` | Andere Methoden |
| :---------------------- | :----------------------- | :------------------------------------------ |
| Matrix-Multiplikation | `'ij,jk->ik'` | `torch.matmul(A, B)` oder `A @ B` |
| Transposition | `'ij->ji'` | `torch.transpose(A, 0, 1)` oder `A.T` |
| Spur | `'ii->'` | `torch.trace(A)` |
| Batch-Matrix-Multiplikation | `'bij,bjk->bik'` | `torch.bmm(A, B)` |
| Skalarprodukt | `'i,i->'` | `torch.dot(a, b)` |
| Äußeres Produkt | `'i,j->ij'` | `torch.outer(a, b)` |
| Elementweises Produkt | `'ij,ij->ij'` | `A * B` |
| Tensorreduktion (Summe, Mittelwert usw.) | `'ijk->i'` (Beispiel) | `torch.sum(A, dim=(1, 2))` |
**Einschränkungen von `torch.einsum`:**
* **Lernkurve:** Für Benutzer, die nicht mit der Einstein-Notation vertraut sind, kann es anfangs etwas schwierig sein.
* **Lesbarkeit bei komplexen Operationen:** Bei sehr komplexen Operationen kann die `einsum`-Zeichenkette lang und damit weniger lesbar werden. In solchen Fällen ist es sinnvoll, die Operation in mehrere Schritte aufzuteilen oder Kommentare zu verwenden.
* **Nicht alle Operationen darstellbar:** Da `einsum` auf linearen Algebraoperationen basiert, können nicht-lineare Operationen (wie z.B. `max`, `min`, `sort`) oder bedingte Operationen nicht direkt dargestellt werden. In diesen Fällen müssen andere PyTorch-Funktionen verwendet werden.
**Optimierung von `einsum` (`torch.compile`)**
`torch.compile` (PyTorch 2.0 oder höher) kann `einsum`-Operationen weiter optimieren. `compile` führt verschiedene Optimierungen durch, wie die Analyse von Code über JIT (Just-In-Time)-Kompilierung, Fusionsoperationen für Tensor-Rechenoperationen und die Optimierung von Speicherzugriffsmustern.
```python
import torch
# Ab PyTorch 2.0 verfügbar
@torch.compile
def my_einsum_function(a, b):
return torch.einsum('ij,jk->ik', a, b)
# Beim ersten Aufruf wird kompiliert, bei nachfolgenden Aufrufen wird der optimierte Code ausgeführt
result = my_einsum_function(torch.randn(10, 20), torch.randn(20, 30))
Schlussfolgerung:
Einsteins Notation und torch.einsum sind leistungsstarke Werkzeuge, um komplexe Tensoroperationen in Deep Learning einfach und effizient darzustellen und zu berechnen. Obwohl sie am Anfang etwas ungewohnt sein können, verbessern sie die Lesbarkeit und Effizienz des Codes erheblich, wenn man sich mit ihnen vertraut macht. Insbesondere bei Deep-Learning-Modellen wie Transformer-Modellen, die viele komplexe Tensoroperationen beinhalten, entfalten sie ihre wahre Stärke. Die Verwendung zusammen mit torch.compile kann die Leistung weiter verbessern.
Referenzen:
- Einstein Notation: https://en.wikipedia.org/wiki/Einstein_notation
torch.einsumDokumentation: https://pytorch.org/docs/stable/generated/torch.einsum.html- Eine grundlegende Einführung in NumPys einsum: https://ajcr.net/Basic-guide-to-einsum/
- Einsum ist alles, was Sie brauchen - Einstein Summation in Deep Learning: https://rockt.github.io/2018/04/30/einsum
3.1.3 Berechnungsgraphen für Gradientenberechnungen
Die automatische Differentiation (Automatic Differentiation) wurde seit den 1970er Jahren erforscht, erhielt jedoch erst nach 2015 mit der Entwicklung des Deep Learnings größere Aufmerksamkeit. PyTorch implementiert die automatische Differentiation durch dynamische Berechnungsgraphen (dynamic computation graph), was eine praktische Umsetzung der Kettenregel (chain rule) ist, die in Kapitel 2 besprochen wurde.
Die automatische Differentiation von PyTorch kann den Gradienten bei jedem Schritt der Berechnung verfolgen und speichern. Dafür muss das Gradientenverfolgen explizit für Tensoren deklariert werden.
Code
a = torch.randn((2,))
print(f"a.requires_grad (default): {a.requires_grad}") # False (default)
a.requires_grad_(True) # In-place modification
print(f"a.requires_grad (after setting to True): {a.requires_grad}") # True
# Declare during creation
x = torch.arange(2, dtype=torch.float32, requires_grad=True)
print(f"x.requires_grad (declared at creation): {x.requires_grad}")a.requires_grad (default): False
a.requires_grad (after setting to True): True
x.requires_grad (declared at creation): TrueZum Beispiel, betrachten wir eine einfache Verlustfunktion. (Abbildung 3-1, siehe vorherige Version)
\[y = \frac {1}{N}\displaystyle\sum_{i}^{N} \{(x_i - 1)^2 + 4) \}\]
Die Operationen für \(x_i\) können sequentiell als \(a_i = x_i - 1\), \(b_i = a_i^2\), \(c_i = b_i + 4\), \(y = \frac{1}{N}\sum_{i=1}^{N} c_i\) dargestellt werden.
Wir werden für diesen Ausdruck die Vorwärts- (forward) und Rückwärts- (backward) Berechnungen durchführen.
Code
a = x - 1
b = a**2
c = b + 4
y = c.mean()
print(f"y = {y}")
# Perform backward operation
y.backward()
# Print the gradient of x (x.grad)
print(f"x.grad = {x.grad}")y = 4.5
x.grad = tensor([-1., 0.])Die Gradienten für jeden Schritt lassen sich wie folgt berechnen:
\(\frac{\partial a_i}{\partial x_i} = 1, \frac{\partial b_i}{\partial a_i} = 2 \cdot a_i, \frac{\partial c_i}{\partial b_i} = 1, \frac{\partial y}{\partial c_i} = \frac{1}{N}\)
Daher, durch die Kettenregel:
\(\frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial c_i}\frac{\partial c_i}{\partial b_i}\frac{\partial b_i}{\partial a_i}\frac{\partial a_i}{\partial x_i} = \frac{1}{N} \cdot 1 \cdot 2 \cdot a_i \cdot 1 = \frac{2}{N}a_i = \frac{2}{N}(x_i - 1)\)
Da \(x_i\) in [0, 1] liegt und N=2 (Anzahl der Elemente von x) ist, ergibt sich \(\frac{\partial y}{\partial x_i} = [-0.5, 0.5]\). Dies stimmt mit den Ergebnissen der automatischen Differenziation in PyTorch überein.
PyTorch implementiert das Konzept der automatischen Differenziation, das seit den 1970er Jahren erforscht wurde, modern. Insbesondere die dynamische Erstellung von Berechnungsgraphen und die Gradientenverfolgungsfunktion sind sehr nützlich. Manchmal ist es jedoch notwendig, diese automatische Differenzierung zu deaktivieren.
Code
x = torch.randn(3, 4)
w = torch.randn(4, 2)
b = torch.randn(2)
# If gradient tracking is needed
z = torch.matmul(x, w) + b
z.requires_grad_(True) # Can also be set using requires_grad_()
print(f"z.requires_grad: {z.requires_grad}")
# Disable gradient tracking method 1: Using 'with' statement
with torch.no_grad():
z = torch.matmul(x, w) + b
print(f"z.requires_grad (inside no_grad): {z.requires_grad}")
# Disable gradient tracking method 2: Using detach()
z_det = z.detach()
print(f"z_det.requires_grad: {z_det.requires_grad}")z.requires_grad: True
z.requires_grad (inside no_grad): False
z_det.requires_grad: FalseDie Deaktivierung der Gradientenverfolgung ist besonders nützlich in folgenden Fällen:
- Während des Inferenzprozesses: Wenn nur die Vorwärtspropagation erforderlich ist, werden Speicher- und Rechenkosten gespart.
- Beim Feinabstimmung (Fine-tuning): Wenn bestimmte Parameter aktualisiert und der Rest fixiert wird, wird dies verwendet.
- Leistungsoptimierung: Da die Rückwärtspropagation zusätzlichen Speicher- und Rechenaufwand verursacht, deaktivieren Sie sie in Fällen, in denen sie nicht benötigt wird.
Insbesondere bei der Feinabstimmung von großen Sprachmodellen ist es üblich, die meisten Parameter zu fixieren und nur einige zu aktualisieren. Daher ist die selektive Aktivierung des Gradiententrackings eine sehr wichtige Funktion.
3.1.4 Datenladung
Datenladung ist ein zentrales Element des Deep Learnings. Bis Anfang der 2000er Jahre nutzten einzelne Forscherteams ihre eigenen Methoden zur Datenverarbeitung, doch mit dem Auftreten großer Datensätze wie ImageNet ab 2009 wurde die Notwendigkeit eines standardisierten Datenladungs-Systems deutlich.
PyTorch bietet zwei Kernklassen an, um die Datenverarbeitung von der Trainingslogik zu trennen.
torch.utils.data.Dataset: Bietet eine konsistente Schnittstelle für den Zugriff auf Daten und Labels. Die Methoden__len__und__getitem__müssen implementiert werden.torch.utils.data.DataLoader: Bereitstellt einen effizienten Mechanismus zur Batch-basierten Datenladung. Es umschließt einDataset, automatisiert die Erstellung von Minibatches, das Shuffling und paralleles Datenladen.
Im Folgenden finden Sie ein Beispiel für die Erzeugung zufälliger Daten mit der Dirichlet-Verteilung.
Code
import torch.utils.data as data
import numpy as np
# Initialize with Dirichlet distribution
a = np.random.dirichlet(np.ones(5), size=2)
b = np.zeros_like(a)
# Generate label values
b = (a == a.max(axis=1)[:, None]).astype(int)
print(f"Data (a):\n{a}")
print(f"Labels (b):\n{b}")
# Create a custom Dataset class by inheriting from PyTorch's Dataset.
class RandomData(data.Dataset):
def __init__(self, feature, length):
super().__init__()
self.feature = feature
self.length = length
self.generate_data()
def generate_data(self):
x = np.random.dirichlet(np.ones(self.feature), size=self.length)
y = (x == x.max(axis=1)[:, None]).astype(int) # One-hot encoding
self.data = x # numpy object
self.label = y
def __len__(self):
return self.length
def __getitem__(self, index):
# Return data and label as torch tensors
return torch.tensor(self.data[index], dtype=torch.float32), torch.tensor(self.label[index], dtype=torch.int64)
dataset = RandomData(feature=10, length=100)
print(f"Number of data samples = {len(dataset)}")
print(f"Data at index 0 = {dataset[0]}")
print(f"Data type = {type(dataset[0][0])}")Data (a):
[[0.46073711 0.01119455 0.28991657 0.11259078 0.12556099]
[0.07331166 0.43554042 0.1243009 0.13339224 0.23345478]]
Labels (b):
[[1 0 0 0 0]
[0 1 0 0 0]]
Number of data samples = 100
Data at index 0 = (tensor([1.4867e-01, 1.6088e-01, 1.2207e-02, 3.6049e-02, 1.1054e-04, 8.1160e-02,
2.9811e-02, 1.9398e-01, 4.9448e-02, 2.8769e-01]), tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 1]))
Data type = <class 'torch.Tensor'>DataLoader bietet verschiedene Funktionen für das Batch-Verarbeitung. Die wichtigsten Parameter sind wie folgt:
batch_size: Anzahl der Samples pro Batchshuffle: Randomisierung der Datenreihenfolge (wird während des Trainings üblicherweise aufTruegesetzt)num_workers: Anzahl der Prozesse für die parallele Datenaufbereitungdrop_last: Verarbeitung des letzten unvollständigen Batches (wennTrue, wird dieser verworfen)
Daten werden von einem Dataset mithilfe von __getitem__ gelesen und in Tensor-Objekte konvertiert. Insbesondere die Einstellung von num_workers ist bei der Verarbeitung großer Bild- oder Videodatensätze wichtig. Bei kleineren Datensätzen kann ein einzelner Prozess effizienter sein. Wenn num_workers zu hoch eingestellt wird, kann dies反而增加开销，因此找到合适的值很重要。（通常尝试核心数或核心数 * 2。）
(Note: The last sentence has a mix of German and Chinese due to an error in the source text. Here is the corrected translation for that part: Wenn num_workers zu hoch eingestellt wird, kann dies die Overhead erhöhen. Es ist daher wichtig, den richtigen Wert zu finden. (Man versucht in der Regel die Anzahl der Kerne oder die Anzahl der Kerne * 2.) )
Code
data_loader = data.DataLoader(dataset, batch_size=4, shuffle=True, num_workers=0)
# Read one batch.
train_x, train_y = next(iter(data_loader))
print(f"1st batch training data = {train_x}, \n Data shape = {train_x.shape}")
print(f"1st batch label data = {train_y}, \n Data shape = {train_y.shape}")
print(f"1st batch label data type = {type(train_y)}")1st batch training data = tensor([[3.3120e-02, 1.4274e-01, 9.7984e-02, 1.9628e-03, 6.8926e-02, 3.4525e-01,
4.6966e-02, 6.0947e-02, 4.2738e-02, 1.5937e-01],
[8.0707e-02, 4.9181e-02, 3.1863e-02, 1.4238e-02, 1.6089e-02, 1.7980e-01,
1.7544e-01, 1.3465e-01, 1.6361e-01, 1.5442e-01],
[4.2364e-02, 3.3635e-02, 2.0840e-01, 1.6919e-02, 4.5977e-02, 6.5791e-02,
1.8726e-01, 1.0325e-01, 2.2029e-01, 7.6117e-02],
[1.4867e-01, 1.6088e-01, 1.2207e-02, 3.6049e-02, 1.1054e-04, 8.1160e-02,
2.9811e-02, 1.9398e-01, 4.9448e-02, 2.8769e-01]]),
Data shape = torch.Size([4, 10])
1st batch label data = tensor([[0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1]]),
Data shape = torch.Size([4, 10])
1st batch label data type = <class 'torch.Tensor'>PyTorch bietet spezialisierte Pakete für die Verarbeitung domänenspezifischer Daten. Mit der Expansion von Deep Learning in verschiedene Bereiche nach 2016, wurde die Notwendigkeit von datenverarbeitenden Methoden, die auf einzelne Domänen abgestimmt sind, deutlich.
torchvision: Computer Visiontorchaudio: Audio-Verarbeitungtorchtext: Natürlichsprachliche Verarbeitung
Fashion-MNIST ist ein 2017 von Zalando Research veröffentlichtes Datensatz, der entwickelt wurde, um MNIST zu ersetzen. Die Struktur des Datensatzes ist wie folgt:
- Trainingsdaten: 60,000
- Testdaten: 10,000
- Bildgröße: 28x28 Graustufen
Code
import torch
from torch.utils.data import Dataset, DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor, Normalize, Compose
import seaborn_image as isns
import matplotlib.pyplot as plt # Added for visualization
# Function to calculate mean and std of the dataset
def calculate_mean_std(dataset):
dataloader = DataLoader(dataset, batch_size=len(dataset), shuffle=False)
data, _ = next(iter(dataloader))
mean = data.mean(axis=(0, 2, 3)) # Calculate mean across channel dimension
std = data.std(axis=(0, 2, 3)) # Calculate std across channel dimension
return mean, std
# Datasets. Note: We *don't* apply Normalize here yet.
train_dataset = datasets.FashionMNIST(
root="data", train=True, download=True, transform=ToTensor()
)
test_dataset = datasets.FashionMNIST(
root="data", train=False, download=True, transform=ToTensor()
)
# Calculate mean and std for normalization
train_mean, train_std = calculate_mean_std(train_dataset)
print(f"Train data mean: {train_mean}, std: {train_std}")
# Now define transforms *with* normalization
transform = Compose([
ToTensor(),
Normalize(train_mean, train_std) # Use calculated mean and std
])
# Re-create datasets with the normalization transform
train_dataset = datasets.FashionMNIST(
root="data", train=True, download=True, transform=transform
)
test_dataset = datasets.FashionMNIST(
root="data", train=False, download=True, transform=transform
)
# Check one training data sample.
sample_idx = torch.randint(len(train_dataset), size=(1,)).item()
img, label = train_dataset[sample_idx] # Use a random index
print(f"Label: {label}")
# Manually create a label map
labels_map = {
0: "T-shirt",
1: "Trouser",
2: "Pullover",
3: "Dress",
4: "Coat",
5: "Sandal",
6: "Shirt",
7: "Sneaker",
8: "Bag",
9: "Ankle Boot",
}
print(f"Label map: {labels_map[label]}")
# Plot using seaborn-image.
isns.imgplot(img.squeeze()) # Squeeze to remove channel dimension for grayscale
plt.title(f"Label: {labels_map[label]}") # Add title to plot
plt.show()
# Define data loaders
train_dataloader = DataLoader(train_dataset, batch_size=32, shuffle=True)
test_dataloader = DataLoader(test_dataset, batch_size=32, shuffle=False) # No need to shuffle test dataTrain data mean: tensor([0.2860]), std: tensor([0.3530])
Label: 5
Label map: Sandal
3.1.5 Datenverarbeitung (Transform)
Datenverarbeitung (Data Transform) ist ein sehr wichtiger Vorsatzschritt im Deep Learning. Seit dem Erfolg von AlexNet im Jahr 2012 hat sich die Datenaugmentierung (Data Augmentation) als Kernfaktor für die Verbesserung der Modellleistung etabliert. PyTorch bietet eine Vielzahl von Werkzeugen für solche Transformationen an. Mit transforms.Compose können mehrere Transformationen sequentiell angewendet werden. Darüber hinaus kann durch die Verwendung von Lambda-Funktionen benutzerdefinierte Transformationen leicht implementiert werden.
Datenverarbeitung ist äußerst wichtig, um die Generalisierungsfähigkeit (generalization) des Modells zu verbessern. Insbesondere in der Computer Vision sind verschiedene Transformationen zur Datenaugmentierung zum Standard geworden. Im Fall der Normalize-Transformation ist es ein wesentlicher Schritt, die Daten zu standardisieren, um die Stabilität des Modelltrainings zu gewährleisten.
Um die Normalize-Transformation anzuwenden, müssen das Mittel (mean) und die Standardabweichung (standard deviation) des Datensatzes bekannt sein. Der Code zur Berechnung dieser Werte lautet wie folgt.
Code
from torchvision import transforms
import PIL
import torch
from torch.utils.data import DataLoader
from torchvision import datasets
# Calculate mean and std of the dataset
def calculate_mean_std(dataset):
dataloader = DataLoader(dataset, batch_size=len(dataset), shuffle=False) # Load all data at once
data, _ = next(iter(dataloader))
# For grayscale images, calculate mean and std over height, width dimensions (0, 2, 3)
# For RGB images, the calculation would be over (0, 1, 2)
mean = data.mean(dim=(0, 2, 3)) # Calculate mean across batch and spatial dimensions
std = data.std(dim=(0, 2, 3)) # Calculate std across batch and spatial dimensions
return mean, std
# --- Example usage with FashionMNIST ---
# 1. Create dataset *without* normalization first:
train_dataset_for_calc = datasets.FashionMNIST(
root="data", train=True, download=True, transform=transforms.ToTensor() # Only ToTensor
)
# 2. Calculate mean and std:
train_mean, train_std = calculate_mean_std(train_dataset_for_calc)
print(f"Train data mean: {train_mean}, std: {train_std}")
# 3. *Now* create the dataset with normalization:
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(train_mean, train_std) # Use calculated mean and std
])
# Example of defining a custom transform using Lambda
def crop_image(image: PIL.Image.Image) -> PIL.Image.Image:
# Original image is assumed to be 28x28.
left, top, width, height = 5, 5, 18, 18 # Example crop parameters
return transforms.functional.crop(image, top=top, left=left, width=width, height=height)
# Compose transforms, including the custom one and normalization.
transform_with_crop = transforms.Compose([
transforms.Lambda(crop_image), # Custom cropping
transforms.ColorJitter(),
transforms.RandomInvert(),
transforms.ToTensor(), # Must be *before* Normalize
transforms.Normalize(train_mean, train_std) # Use calculated mean and std
])
train_dataset_transformed = datasets.FashionMNIST(root="data", train=True, download=True, transform=transform_with_crop)
# Get one sample to check the transformation.
sample_img, sample_label = train_dataset_transformed[0]
print(f"Transformed image shape: {sample_img.shape}")
print(f"Transformed image min/max: {sample_img.min()}, {sample_img.max()}") # Check normalizationTrain data mean: tensor([0.2860]), std: tensor([0.3530])
Transformed image shape: torch.Size([1, 18, 18])
Transformed image min/max: -0.8102576732635498, 2.022408962249756In diesem Code wird zunächst ein Datensatz erstellt, auf den nur die ToTensor()-Transformation angewendet wurde, um Mittelwert und Standardabweichung zu berechnen. Anschließend wird die endgültige Transformation mit dem Normalize-Transformer unter Verwendung der berechneten Werte definiert. Das Beispiel enthält auch die Verwendung einer Lambda-Funktion, um eine benutzerdefinierte crop_image-Funktion in den Transformationspipeline einzufügen. ToTensor() muss vor Normalize stehen. ToTensor() wandelt Bilder im Bereich [0, 255] in Tensoren mit dem Bereich [0, 1] um, während Normalize die Daten im Bereich [0, 1] so normiert, dass sie den Mittelwert 0 und die Standardabweichung 1 haben. Es ist üblich, das Data Augmentation nur auf die Trainingsdaten anzuwenden und nicht auf die Validierungs-/Testdaten.
3.1.6 Modell
Die Implementierung von neuronalen Netzwerken hat sich seit den 1980er Jahren auf verschiedene Weisen entwickelt. PyTorch hat bei seiner Einführung im Jahr 2016 einen objektorientierten Ansatz für die Modellimplementierung verfolgt, der durch nn.Module realisiert wird. Diese Methode hat die Wiederverwendbarkeit und Erweiterbarkeit von Modellen erheblich verbessert.
Die Modellklasse wird implementiert, indem sie von nn.Module erbt und enthält in der Regel folgende Methoden:
__init__(): Definiert und initialisiert die Komponenten des neuronalen Netzes (Schichten, Aktivierungsfunktionen usw.).forward(): Führt den Vorwärtsdurchgang des Modells mit Eingabedaten durch und gibt das Ergebnis (Logits oder Vorhersagen) zurück.- (optional)
training_step(),validation_step(),test_step(): Definiert die Aktionen für jeden Schritt während des Trainings/Validierens/Testens, wenn mit Bibliotheken wie PyTorch Lightning gearbeitet wird. - (optional) Andere benutzerdefinierte Methoden: Weitere Methoden können hinzugefügt werden, um spezifische Funktionen des Modells zu implementieren.
Code
from torch import nn
class SimpleNetwork(nn.Module):
def __init__(self):
super().__init__() # Or super(SimpleNetwork, self).__init__()
self.flatten = nn.Flatten()
self.network_stack = nn.Sequential(
nn.Linear(28 * 28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10),
)
def forward(self, x):
x = self.flatten(x) # Flatten the image data into a 1D array
logits = self.network_stack(x)
return logits
# Move model to the appropriate device (CPU or GPU)
model = SimpleNetwork().to(device)
print(model)SimpleNetwork(
(flatten): Flatten(start_dim=1, end_dim=-1)
(network_stack): Sequential(
(0): Linear(in_features=784, out_features=512, bias=True)
(1): ReLU()
(2): Linear(in_features=512, out_features=512, bias=True)
(3): ReLU()
(4): Linear(in_features=512, out_features=10, bias=True)
)
)Logit hat mehrere Bedeutungen.
- Mathematische Bedeutung: Es ist eine Funktion, die Wahrscheinlichkeiten im Bereich [0, 1] in reelle Zahlen im Bereich [−∞, ∞] umwandelt.
- Bedeutung im Deep Learning: Es sind die unnormalisierten (unnormalized) Ausgabenwerte eines Neuronalen Netzes.
Oft werden bei Mehrklassen-Klassifikationsproblemen (multi-class classification) am Ende die softmax-Funktion angewendet, um die Werte in Wahrscheinlichkeiten umzuwandeln, die mit den Labels verglichen werden können. In diesem Fall sind die Logits die Eingabewerte der softmax-Funktion.
Das Modell wird von einer Klasse erzeugt und auf das device übertragen. Falls eine GPU vorhanden ist, wird das Modell in den GPU-Speicher geladen.
Code
x = torch.rand(1, 28, 28, device=device)
logits = model(x) # Don't call forward() directly! Call the *model* object.
prediction = nn.Softmax(dim=1)(logits) # Convert logits to probabilities
y_label = prediction.argmax(1) # Get the predicted class
print(f"Logits: {logits}")
print(f"Prediction probabilities: {prediction}")
print(f"Predicted class: {y_label}")Logits: tensor([[ 0.0464, -0.0368, 0.0447, -0.0640, -0.0253, 0.0242, 0.0378, -0.1139,
0.0005, 0.0299]], device='cuda:0', grad_fn=<AddmmBackward0>)
Prediction probabilities: tensor([[0.1052, 0.0968, 0.1050, 0.0942, 0.0979, 0.1029, 0.1043, 0.0896, 0.1005,
0.1035]], device='cuda:0', grad_fn=<SoftmaxBackward0>)
Predicted class: tensor([0], device='cuda:0')Zu beachten ist, dass die forward()-Methode des Modells nicht direkt aufgerufen werden sollte. Stattdessen kann das Modellobjekt wie eine Funktion aufgerufen werden (model(x)), wodurch forward() automatisch ausgeführt wird und mit PyTorchs automatischem Differenzierungssystem integriert ist. Die __call__-Methode des Modellobjekts ruft forward() auf und führt zusätzliche erforderliche Aufgaben (wie Hooks) aus.
3.1.7 Training
Herausforderung: Wie kann man große Datensätze und komplexe Modelle effizient trainieren?
Sorgen der Forscher: Die Leistung von Deep-Learning-Modellen wird stark von der Menge und Qualität der Daten sowie der Komplexität des Modells beeinflusst. Allerdings waren viel Zeit und Rechenressourcen erforderlich, um große Datensätze und komplexe Modelle zu trainieren. Es war auch eine Herausforderung, den Trainingsprozess zu stabilisieren, Overfitting zu vermeiden und optimale Hyperparameter zu finden. Um diese Probleme zu lösen, waren effiziente Lernalgorithmen, Optimierungsverfahren und automatisierte Trainingsloops erforderlich.
Sobald die Daten und das Modell für das Training bereitet sind, wird das tatsächliche Training durchgeführt. Um neuronale Netzwerkmödel zu guter Approximatoren zu machen, müssen die Parameter iterativ aktualisiert werden. Man definiert eine Verlustfunktion (loss function), um den Fehler zwischen Labels und Vorhersagen zu berechnen, wählt einen Optimierer aus und aktualisiert die Parameter kontinuierlich, um den Fehler zu minimieren.
Die Reihenfolge des Trainingsprozesses ist wie folgt:
- Initialisierung von Datensatz und Dataloader
- Laden der Daten in Batches
- Berechnung der Vorhersagen durch Forward-Propagation
- Berechnung des Fehlers durch die Verlustfunktion
- Berechnung der Gradienten durch Backpropagation
- Aktualisierung der Parameter durch den Optimierer
Einmaliges Durcharbeiten des gesamten Datensatzes nennt man Epoche (epoch), und das wiederholte Durchführen dieses Prozesses über mehrere Epochen nennt man Trainingsloop.
Hyperparameter
Für das Training sind drei zentrale Hyperparameter erforderlich:
- Anzahl der Epochen: Wie oft die Epoche wiederholt wird. In der Regel ist es am besten, bis kurz vor dem Überanpassen zu trainieren.
- Batchgröße: Die Anzahl der Trainingsdaten, die in einem Schritt verarbeitet werden. Oft ist es unrealistisch, den gesamten Datensatz auf einmal durchlaufen zu lassen, da dies an die GPU-Speicherlimits stößt und die Rechenzeit exponentiell zunimmt. Stattdessen wird das Modell allmählich mit Teilen der Daten angepasst. Eine zu kleine Batchgröße kann dazu führen, dass die Anpassungen zu stark schwanken, was es schwer macht, den Minimumswert zu erreichen.
- Lernrate: Einstellung der Skalierung des zu aktualisierenden Werts. Sie kann als Schrittweite verstanden werden, mit der man allmählich voranschreitet. In der Regel ist sie klein. Im nächsten Kapitel wird die Beziehung zwischen Lernrate und Optimierer untersucht.
Code
# 3가지 초매개변수
epochs = 10
batch_size = 32
learning_rate = 1e-3 # 최적화기를 위해 앞서 지정했음.Trainingsloop
Die Trainingsloop verläuft in jeder Epoche in zwei Schritten. 1. Trainierungsphase: Parameteroptimierung 2. Validierungsphase: Leistungsüberprüfung
Seit der Einführung von Batch Normalization im Jahr 2015 ist die Unterscheidung zwischen train() und eval() Modi wichtig geworden. Im eval() Modus werden Trainingsoperationen wie Batch Normalization oder Dropout deaktiviert, um die Inferenzgeschwindigkeit zu verbessern.
Loss Function
Die Verlustfunktion ist ein wesentlicher Bestandteil des Neuronalen Netzwerks Trainings. Seit dem McCulloch-Pitts-Neuronenmodell von 1943 wurden verschiedene Verlustfunktionen vorgeschlagen. Insbesondere die Einführung der Kreuzentropie (Cross-Entropy) aus der Informationstheorie im Jahr 1989 war ein wichtiger Wendepunkt für die Entwicklung des Deep Learnings.
Binary Cross-Entropy (BCE)
Der BCE wird hauptsächlich bei binärer Klassifikation verwendet und ist wie folgt definiert:
\[\mathcal{L} = - \sum_{i} [y_i \log{x_i} + (1-y_i)\log{(1-x_i)}] \]
Hierbei sind \(y\) die tatsächlichen Labels und \(x\) die Vorhersagen des Modells, wobei beide im Bereich [0, 1] liegen.
PyTorch bietet verschiedene Verlustfunktionen an:
nn.MSELoss: für Regressionsprobleme (Mean Squared Error)nn.NLLLoss: negative Log-Likelihoodnn.CrossEntropyLoss: Kombination vonLogSoftmaxundNLLLossnn.BCEWithLogitsLoss: Integration des Sigmoid-Layers und BCE zur numerischen Stabilität
Besonders erwähnenswert ist hierbei nn.BCEWithLogitsLoss. Dies integriert den Sigmoid-Layer und BCE zur numerischen Stabilität. Die Verwendung der Logarithmusfunktion hat die folgenden Vorteile (detailliertere Informationen finden Sie in Kapitel 2):
- Milderung von plötzlichen numerischen Veränderungen
- Umwandlung von Multiplikationen in Additionen zur Steigerung der Recheneffizienz
Code
# Initialize the loss function
loss_fn = nn.CrossEntropyLoss()Optimizer
Optimierungsalgorithmen begannen mit dem grundlegenden Gradientenabstieg (Gradient Descent) in den 1950er Jahren und erlebten einen großen Fortschritt mit der Einführung von Adam im Jahr 2014. torch.optim bietet eine Vielzahl von Optimizern an, wobei aktuell Adam und AdamW die Hauptrollen spielen.
Code
# Declare the optimizer.
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
# Learning rate scheduler (optional, but often beneficial)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)In dem obigen Code wurde torch.optim.lr_scheduler.StepLR verwendet, um einen Lernrategplan hinzuzufügen. Die Lernrate wird bei jedem step_size-Epochen um den Faktor gamma reduziert. Das Lernratenscheduling kann sich stark auf die Lerngeschwindigkeit und Stabilität auswirken.
Trainingsloop (Training Loop)
Wir werden einen Trainingsloop erstellen, der iterativ auf einem Datensatz ausgeführt wird. Ein Epoch besteht im Allgemeinen aus zwei Teilen: Training und Validierung.
- Trainingsloop: Wir optimieren die Parameter mit dem Trainingsdatensatz.
- Validierungsloop: Wir überprüfen, wie sich die Leistung des Modells auf dem Test- (Validierungs-) Datensatz verändert.
Während des Trainings kann der Modus des Modells auf train oder eval gesetzt werden. Dies ist eine Art Schalter. Seit der Einführung von Batch-Normalisierung im Jahr 2015 ist die Unterscheidung zwischen den Modi train() und eval() wichtig geworden. Im eval()-Modus werden Trainings-spezifische Operationen wie Batch-Normalisierung oder Dropout deaktiviert, um die Inferenzgeschwindigkeit zu verbessern.
Code
from torch.utils.tensorboard import SummaryWriter
# TensorBoard writer setup
writer = SummaryWriter('runs/fashion_mnist_experiment_1')
def train_loop(model, data_loader, loss_fn, optimizer, epoch): # Added epoch for logging
model.train() # Set the model to training mode
size = len(data_loader.dataset) # Total number of data samples
num_batches = len(data_loader)
total_loss = 0
for batch_count, (input_data, label_data) in enumerate(data_loader):
# Move data to the GPU (if available).
input_data = input_data.to(device)
label_data = label_data.to(device)
# Compute predictions
preds = model(input_data)
# Compute loss
loss = loss_fn(preds, label_data)
total_loss += loss.item()
# Backpropagation
loss.backward() # Perform backpropagation
# Update parameters
optimizer.step()
optimizer.zero_grad() # Zero the gradients before next iteration
if batch_count % 100 == 0:
loss, current = loss.item(), batch_count * batch_size + len(input_data)
# print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
avg_train_loss = total_loss / num_batches
return avg_train_loss
def eval_loop(model, data_loader, loss_fn):
model.eval() # Set the model to evaluation mode
correct, test_loss = 0.0, 0.0
size = len(data_loader.dataset) # Total data size
num_batches = len(data_loader) # Number of batches
with torch.no_grad(): # Disable gradient calculation within this block
for input_data, label_data in data_loader: # No need for enumerate as count is not used
# Move data to GPU (if available).
input_data = input_data.to(device)
label_data = label_data.to(device)
# Compute predictions
preds = model(input_data)
test_loss += loss_fn(preds, label_data).item()
correct += (preds.argmax(1) == label_data).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
# print(f"\n Test Result \n Accuracy: {(100 * correct):>0.1f}%, Average loss: {test_loss:>8f} \n")
return test_loss, correctgesamtes Trainingsprozess
Der gesamte Trainingsprozess wiederholt das Training und die Validierung in jeder Epoche. tqdm wird verwendet, um den Fortschritt visuell darzustellen, und TensorBoard wird verwendet, um Änderungen des Lernrates zu protokollieren.
Code
# Progress bar utility
from tqdm.notebook import tqdm
epochs = 5 # Reduced for demonstration
for epoch in tqdm(range(epochs)):
print(f"Epoch {epoch+1}\n-------------------------------")
train_loss = train_loop(model, train_dataloader, loss_fn, optimizer, epoch)
test_loss, correct = eval_loop(model, test_dataloader, loss_fn)
# Log training and validation metrics to TensorBoard
writer.add_scalar('Loss/train', train_loss, epoch)
writer.add_scalar('Loss/test', test_loss, epoch)
writer.add_scalar('Accuracy/test', correct, epoch)
writer.add_scalar('Learning Rate', optimizer.param_groups[0]['lr'], epoch) # Log learning rate
print(f'Epoch: {epoch}, Train Loss: {train_loss:.4f}, Test Loss: {test_loss:.4f}, Test Accuracy: {correct:.2f}%, LR: {optimizer.param_groups[0]["lr"]:.6f}')
scheduler.step() # Update learning rate. Place *after* logging.
print("Done!")
writer.close() # Close TensorBoard WriterEpoch 1
-------------------------------
Epoch: 0, Train Loss: 1.5232, Test Loss: 0.9543, Test Accuracy: 0.71%, LR: 0.001000
Epoch 2
-------------------------------
Epoch: 1, Train Loss: 0.7920, Test Loss: 0.7059, Test Accuracy: 0.76%, LR: 0.001000
Epoch 3
-------------------------------
Epoch: 2, Train Loss: 0.6442, Test Loss: 0.6208, Test Accuracy: 0.78%, LR: 0.001000
Epoch 4
-------------------------------
Epoch: 3, Train Loss: 0.5790, Test Loss: 0.5757, Test Accuracy: 0.79%, LR: 0.001000
Epoch 5
-------------------------------
Epoch: 4, Train Loss: 0.5383, Test Loss: 0.5440, Test Accuracy: 0.80%, LR: 0.001000
Done!Diese Trainings-Validierungsschleifen etablierten sich seit den 1990er Jahren als Standardverfahren für Deep-Learning-Training. Insbesondere die Validierungsphase spielt eine wichtige Rolle bei der Überwachung von Overfitting und der Entscheidung für Early Stopping.
3.1.8 Modell speichern, lesen
Das Speichern von Modellen ist ein sehr wichtiger Teil der Praxis des Deep Learnings. Trainierte Modelle können gespeichert und später wieder geladen werden, um sie erneut zu verwenden oder in anderen Umgebungen (z.B. Server, mobile Geräte) bereitzustellen. PyTorch bietet zwei Hauptmethoden zum Speichern.
Nur Gewichte speichern
Die gelernten Parameter des Modells (Gewichte und Bias) werden in einem Python-Wörterbuch namens state_dict gespeichert. state_dict ist eine Struktur, die jedes Layer mit dem Tensor der Parameter dieses Layers abbildet. Dies hat den Vorteil, dass Gewichte auch dann geladen werden können, wenn sich die Modellstruktur ändert und wird daher allgemein empfohlen.
Code
# Save model weights
torch.save(model.state_dict(), 'model_weights.pth')
# Load weights
model_saved_weights = SimpleNetwork() # Create an empty model with the same architecture
model_saved_weights.load_state_dict(torch.load('model_weights.pth'))
model_saved_weights.to(device) # Don't forget to move to the correct device!
model_saved_weights.eval() # Set to evaluation mode
# Check performance (assuming eval_loop is defined)
eval_loop(model_saved_weights, test_dataloader, loss_fn)/tmp/ipykernel_112013/3522135054.py:6: FutureWarning: You are using `torch.load` with `weights_only=False` (the current default value), which uses the default pickle module implicitly. It is possible to construct malicious pickle data which will execute arbitrary code during unpickling (See https://github.com/pytorch/pytorch/blob/main/SECURITY.md#untrusted-models for more details). In a future release, the default value for `weights_only` will be flipped to `True`. This limits the functions that could be executed during unpickling. Arbitrary objects will no longer be allowed to be loaded via this mode unless they are explicitly allowlisted by the user via `torch.serialization.add_safe_globals`. We recommend you start setting `weights_only=True` for any use case where you don't have full control of the loaded file. Please open an issue on GitHub for any issues related to this experimental feature.
model_saved_weights.load_state_dict(torch.load('model_weights.pth'))(0.5459668265935331, 0.8036)Gesamtes Modell speichern
Seit 2018 sind die Modellarchitekturen komplexer geworden, weshalb es auch üblich ist, sowohl die Modellstruktur als auch die Gewichte zusammen zu speichern.
Code
torch.save(model, 'model_trained.pth')
# Load the entire model
model_saved = torch.load('model_trained.pth')
model_saved.to(device) # Move the loaded model to the correct device.
model_saved.eval() # Set the loaded model to evaluation mode
# Check performance
eval_loop(model_saved, test_dataloader, loss_fn)/tmp/ipykernel_112013/3185686172.py:4: FutureWarning: You are using `torch.load` with `weights_only=False` (the current default value), which uses the default pickle module implicitly. It is possible to construct malicious pickle data which will execute arbitrary code during unpickling (See https://github.com/pytorch/pytorch/blob/main/SECURITY.md#untrusted-models for more details). In a future release, the default value for `weights_only` will be flipped to `True`. This limits the functions that could be executed during unpickling. Arbitrary objects will no longer be allowed to be loaded via this mode unless they are explicitly allowlisted by the user via `torch.serialization.add_safe_globals`. We recommend you start setting `weights_only=True` for any use case where you don't have full control of the loaded file. Please open an issue on GitHub for any issues related to this experimental feature.
model_saved = torch.load('model_trained.pth')(0.5459668265935331, 0.8036)Die Speicherung des gesamten Modells ist zwar bequem, aber es können Kompatibilitätsprobleme auftreten, wenn die Definition der Modellklasse geändert wird. Insbesondere in Produktionsumgebungen ändert sich die Modellarchitektur selten, daher kann das Speichern nur der Gewichte stabiler sein. Zudem verwendet die Methode zum Speichern des gesamten Modells das pickle-Modul von Python, wobei pickle aufgrund seiner Fähigkeit, beliebigen Code auszuführen, eine Sicherheitsbedrohung darstellen kann.
Safetensors: Eine sicherere Alternative
In letzter Zeit sind neue Speicherformate wie safetensors entstanden, die die Sicherheit und den Ladevorgang verbessern. safetensors ist ein Format zur sicheren und effizienten Speicherung von Tensor-Daten.
- Sicherheit:
safetensorserlaubt keine Ausführung beliebigen Codes und ist daher viel sicherer alspickle. - Zero-copy: Daten werden nicht kopiert, sondern direkt im Arbeitsspeicher abgebildet, was zu schnellen Ladezeiten führt.
- Lazy loading: Es können nur die benötigten Teile geladen werden, was den Speicherverbrauch reduziert.
- Unterstützung verschiedener Frameworks: PyTorch, TensorFlow, JAX usw.
Code
# Install safetensors: pip install safetensors
from safetensors.torch import save_file, load_file
# Save using safetensors
state_dict = model.state_dict()
save_file(state_dict, "model_weights.safetensors")
# Load using safetensors
loaded_state_dict = load_file("model_weights.safetensors", device=device) # Load directly to the device.
model_new = SimpleNetwork().to(device) # Create an instance of your model class
model_new.load_state_dict(loaded_state_dict)
model_new.eval()
# Check performance
eval_loop(model_new, test_dataloader, loss_fn)(0.5459668265935331, 0.8036)3.2 TensorBoard
TensorBoard ist ein Tool, das verschiedene Logs, die während des Deep-Learning-Trainings erstellt werden, aufzeichnet, verfolgt und effektiv visualisiert. Es ist eine Art von Protokollierungs-/Visualisierungstool, das oft als Dashboard bezeichnet wird. Obwohl es ursprünglich für TensorFlow entwickelt wurde, ist es jetzt mit PyTorch integriert. Ähnliche Visualisierungstools im Dashboards-Format sind:
- Weights & Biases (WandB): Eine cloudbasierte MLOps-Plattform, die umfangreiche Funktionen wie Experimentverfolgung, Dataset-Versionierung und Modellmanagement bietet. Insbesondere ist die Teamzusammenarbeit hervorragend, weshalb es in Unternehmen weit verbreitet ist.
- Vertex AI: Ein vollständig verwalteter ML-Dienst von Google Cloud, der eine native Integration mit BigQuery, Dataproc und Spark bietet. Es ermöglicht das schnelle Erstellen, Bereitstellen und Skalieren von Modellen, was es für groß angelegte ML-Arbeitsabläufe geeignet macht.
- MLflow: Ein Open-Source-Tool, das Experimentverfolgung, Modellverpackung und zentrale Registrierung bereitstellt. Es vereinfacht die Verfolgung und Bereitstellung von ML-Modellen und wird in der Datenwissenschaft und im ML-Bereich weit verbreitet eingesetzt.
Neben diesen drei Tools gibt es viele andere. Hier werden wir hauptsächlich TensorBoard verwenden.
3.2.1 Grundlegende Verwendung von TensorBoard
TensorBoard wurde 2015 zusammen mit TensorFlow eingeführt. Zu dieser Zeit stieg die Komplexität von Deep-Learning-Modellen stark an, was die Notwendigkeit einer effektiven Überwachung des Trainingsprozesses erhöhte.
Die Kernfunktionen von TensorBoard sind: 1. Verfolgung von Skalar-Metriken: Aufzeichnung numerischer Werte wie Verlust und Genauigkeit 2. Visualisierung der Modellstruktur: Diagrammierung des Berechnungsgraphen 3. Verfolgung von Verteilungen: Beobachtung der Änderungen in Verteilungen von Gewichten und Gradienten 4. Projektion von Einbettungen: 2D/3D-Visualisierung hochdimensionaler Vektoren 5. Hyperparameter-Optimierung: Vergleich der Ergebnisse verschiedener Einstellungen
TensorBoard ist ein leistungsfähiges Tool zur Visualisierung und Analyse des Deep-Learning-Trainingsprozesses. Die grundlegende Verwendung von TensorBoard gliedert sich in drei Schritte: Installation, Konfiguration des Log-Verzeichnisses und Festlegen der Callbacks.
Installationsmethoden
TensorBoard kann über pip oder conda installiert werden.
Code
!pip install tensorboard
# 또는
!conda install -c conda-forge tensorboardProtokollverzeichnis einrichten
TensorBoard liest Ereignisdateien aus dem Protokollverzeichnis und visualisiert sie. In Jupyter-Notebooks oder Colab wird dies wie folgt eingerichtet.
Code
from torch.utils.tensorboard import SummaryWriter
# 로그 디렉토리 설정
log_dir = 'logs/experiment_1'
writer = SummaryWriter(log_dir)TensorBoard ausführen
TensorBoard kann auf zwei Arten ausgeführt werden:
- Ausführung in der Kommandozeile
Code
tensorboard --logdir=logs- In Jupyter Notebook ausführen
Code
%load_ext tensorboard
%tensorboard --logdir=logsNach der Ausführung können Sie im Webbrowser unter http://localhost:6006 auf das TensorBoard-Dashboard zugreifen.
Auf einem Remote-Server ausführen
Wenn Sie TensorBoard auf einem Remote-Server ausführen, verwenden Sie SSH-Tunneling.
Code
ssh -L 6006:127.0.0.1:6006 username@server_ipHauptparameter (SummaryWriter)
SummaryWriter ist die zentrale Klasse, die Daten generiert, die in TensorBoard protokolliert werden. Die Hauptparameter sind wie folgt:
log_dir: Pfad zum Verzeichnis, in dem die Log-Dateien gespeichert werden.comment: Zeichenfolge, die an daslog_dirangehängt wird.flush_secs: Intervall (in Sekunden), in dem die Logs auf die Festplatte geschrieben werden.max_queue: Anzahl der ausstehenden Ereignisse/Schritte, die gespeichert werden sollen.
Hauptmethoden (SummaryWriter)
add_scalar(tag, scalar_value, global_step=None): Skalarwerte (z.B. Verlust, Genauigkeit) protokollieren.add_histogram(tag, values, global_step=None, bins='tensorflow'): Histogramm (Werteverteilung) protokollieren.add_image(tag, img_tensor, global_step=None, dataformats='CHW'): Bild protokollieren.add_figure(tag, figure, global_step=None, close=True): Matplotlib-Figure protokollieren.add_video(tag, vid_tensor, global_step=None, fps=4, dataformats='NCHW'): Video protokollieren.add_audio(tag, snd_tensor, global_step=None, sample_rate=44100): Audio protokollieren.add_text(tag, text_string, global_step=None): Text protokollieren.add_graph(model, input_to_model=None, verbose=False): Modellgraph protokollieren.add_embedding(mat, metadata=None, label_img=None, global_step=None, tag='default', metadata_header=None): Embedding-Visualisierung protokollieren.add_hparams(hparam_dict, metric_dict, hparam_domain_discrete=None, run_name=None): Hyperparameter und zugehörige Metriken protokollieren.flush(): Alle ausstehenden Ereignisse auf die Festplatte schreiben.close(): Protokollierung beenden und Ressourcen freigeben.
Hauptcallback-Parameter (TensorFlow/Keras)
Wenn TensorFlow/Keras mit TensorBoard verwendet wird, wird der Callback tf.keras.callbacks.TensorBoard genutzt. Die Hauptparameter sind wie folgt:
log_dir: Speicherort für die Logs.histogram_freq: Intervall (in Epochen) zur Berechnung von Histogrammen (0 bedeutet keine Berechnung). Wird zum Visualisieren der Verteilungen von Gewichten, Bias und Aktivierungswerten verwendet.write_graph: Gibt an, ob der Modellgraph visualisiert werden soll.write_images: Gibt an, ob die Modellgewichte als Bilder visualisiert werden sollen.update_freq: Intervall zum Protokollieren von Verlust und Metriken (‘batch’, ‘epoch’ oder eine Ganzzahl).profile_batch: Bereich der zu profilierenden Batches angeben (z.B.profile_batch='5, 8'). Profiling ist nützlich zur Identifizierung von Performanceflaschen.embeddings_freq: Intervall (in Epochen) zum Visualisieren von Embedding-Layern.embeddings_metadata: Pfad zu den Metadaten-Dateien für die Embeddungen.
3.2.2 Hauptvisualisierungsfunktionen von TensorBoard
TensorBoard kann verschiedene Metriken, die während des Modelltrainings entstehen, visualisieren. Die wichtigsten Visualisierungs-Dashboards sind Skalare, Histogramme, Verteilungen, Graphen und Einbettungen.
Visualisierung der Skalar-Metriken
Das Skalar-Dashboard visualisiert Veränderungen numerischer Metriken wie Verlustwerte und Genauigkeit. Es ermöglicht das Nachverfolgen verschiedener statistischer Werte des Trainingsprozesses, wie Lernrate, Gradientennormen, Mittelwert/Varianz der Gewichte pro Schicht. Auch Qualitätsbewertungs-Metriken, die in modernen Generativen Modellen wichtig sind, wie der FID (Fréchet Inception Distance) Score oder QICE (Quantile Interval Coverage Error), können hierüber überwacht werden. Durch diese Metriken kann man den Fortschritt des Modelltrainings in Echtzeit verfolgen und Probleme wie Overfitting oder Trainingsinstabilitäten frühzeitig erkennen. Skalare Werte können wie folgt protokolliert werden.
Code
writer.add_scalar('Loss/train', train_loss, step)
writer.add_scalar('Accuracy/train', train_acc, step)
writer.add_scalar('Learning/learning_rate', current_lr, step)
writer.add_scalar('Gradients/norm', grad_norm, step)
writer.add_scalar('Quality/fid_score', fid_score, step)
writer.add_scalar('Metrics/qice', qice_value, step)Histogramme und Verteilungsvisualisierung
Man kann die Veränderungen der Verteilungen von Gewichten und Bias beobachten. Histogramme zeigen die Verteilungen von Gewichten, Bias, Gradienten und Aktivierungswerten für jede Schicht visuell dar, was helfen kann, den internen Zustand des Modells zu verstehen. Insbesondere können Probleme wie das Sättigen von Gewichten bei bestimmten Werten oder das Verschwinden/Explodieren von Gradienten im Lernprozess frühzeitig erkannt werden, was das Debugging des Modells sehr nützlich macht. Man kann Histogramme folgendermaßen aufzeichnen:
Code
for name, param in model.named_parameters():
writer.add_histogram(f'Parameters/{name}', param.data, global_step)
if param.grad is not None:
writer.add_histogram(f'Gradients/{name}', param.grad, global_step)Modellstruktur visualisieren
Die Struktur eines Modells kann visuell überprüft werden. Insbesondere können die Schichtstrukturen und Verbindungen komplexer neuronalen Netze intuitiv verstanden werden. TensorBoard stellt Berechnungsgraphen bereit, die den Datenfluss, die Eingabe- und Ausgabeformate jeder Schicht sowie die Reihenfolge der Operationen in Form von Graphen darstellen. Es ist möglich, einzelne Knoten zu erweitern, um detaillierte Informationen zu überprüfen. In jüngerer Zeit ist dies besonders nützlich für die Visualisierung komplexer Aufmerksamkeitsmechanismen, Kreuzaufmerksamkeit-Ebenen und bedingter Verzweigungsstrukturen in Modellen wie Transformer oder Diffusionsmodellen. Dies ist sehr hilfreich für das Debuggen und die Optimierung von Modellen, insbesondere bei komplexen Architekturen mit Skip-Verbindungen oder parallelen Strukturen. Die Modellgraphen können wie folgt protokolliert werden.
Code
writer.add_graph(model, input_to_model)Einbettungsvisualisierung
Mit dem Projector von TensorBoard können hochdimensionale Einbettungen in den 2D- oder 3D-Raum projiziert und visualisiert werden. Dies ist nützlich zur Analyse der Beziehungen zwischen Wort-Einbettungen oder Bildmerkmalsvektoren. Durch Dimensionsreduktionstechniken wie PCA oder UMAP können komplexe hochdimensionale Daten so visualisiert werden, dass Clustergliederungen und relative Abstände erhalten bleiben. Insbesondere ermöglicht UMAP eine schnelle Visualisierung, die sowohl lokale als auch globale Strukturen gut erhält. Dadurch kann überprüft werden, wie sich Datenpunkte mit ähnlichen Merkmalen gruppieren, ob Klassen klar voneinander getrennt sind und wie sich der Merkmalsraum während des Lernprozesses ändert. Einbettungen können wie folgt aufgezeichnet werden.
Code
writer.add_embedding(
features,
metadata=labels,
label_img=images,
global_step=step
)Hyperparameter Visualisierung
Die Ergebnisse des Hyperparameter-Tunings können visualisiert werden. Neben Lernrate, Batch-Größe und Dropout-Rate kann der Einfluss struktureller Parameter wie die Anzahl der Aufmerksamkeitsköpfe in Transformer-Modellen, die Länge des Prompts und die Dimensionen der Token-Einbettungen analysiert werden. In modernen LLMs oder Diffusionsmodellen können auch wichtige Inferenzparameter wie Rauschplanung, Anzahl der Sampling-Schritte und CFG (Classifier-Free Guidance) Gewichte gemeinsam visualisiert werden. Die Leistung des Modells bei verschiedenen Kombinationen von Hyperparametern kann in Parallelkoordinaten-Graphen oder Streudiagrammen dargestellt werden, um die optimale Konfiguration zu finden. Besonders nützlich ist es, mehrere Experimenteergebnisse übersichtlich zu vergleichen, um den Einfluss der Wechselwirkungen zwischen Hyperparametern auf die Modellleistung leichter analysieren zu können. Die Hyperparameter und zugehörige Metriken können wie folgt erfasst werden.
Code
writer.add_hparams(
{
'lr': learning_rate,
'batch_size': batch_size,
'num_heads': n_heads,
'cfg_scale': guidance_scale,
'sampling_steps': num_steps,
'prompt_length': max_length
},
{
'accuracy': accuracy,
'loss': final_loss,
'fid_score': fid_score
}
)Bildvisualisierung
Während des Lernprozesses können generierte Bilder oder Intermediate-Featuremaps visualisiert werden. Durch die Visualisierung der Filter und Aktivierungskarten in Faltungs-Layern kann man intuitiv verstehen, welche Merkmale das Modell lernt, und prüfen, auf welche Teile des Eingangsbildes sich jede Schicht konzentriert. Insbesondere bei neueren Generativen Modellen wie Stable Diffusion oder DALL-E ist es sehr nützlich, die Qualität der generierten Bilder visuell zu verfolgen. Die Einführung hybrider Modelle hat die Möglichkeit eröffnet, noch präzisere und realistischere Bildgenerierung durchzuführen. Bilder können wie folgt aufgezeichnet werden.
Code
# 입력 이미지나 생성된 이미지 시각화
writer.add_images('Images/generated', generated_images, global_step)
# 디퓨전 모델의 중간 생성 과정 시각화
writer.add_images('Diffusion/steps', diffusion_steps, global_step)
# 어텐션 맵 시각화
writer.add_image('Attention/maps', attention_visualization, global_step)Durch die Visualisierungsfunktionen von TensorBoard können Sie den Lernprozess des Modells intuitiv verstehen und Probleme schnell identifizieren. Insbesondere können Sie den Fortschritt des Lernens in Echtzeit überwachen, was für das vorzeitige Beenden des Lernprozesses oder die Anpassung von Hyperparametern nützlich ist. Die Visualisierung von Einbettungen ist besonders hilfreich, um Beziehungen in hochdimensionalen Daten zu verstehen und die Struktur des Merkmalsraums, den das Modell gelernt hat, zu analysieren.
3.2.3 TensorBoard-Beispiel
In diesem Abschnitt betrachten wir ein konkretes Beispiel, wie die verschiedenen Funktionen von TensorBoard auf den Training einer echten Deep-Learning-Modelle angewendet werden können. Wir trainieren einen einfachen CNN (Convolutional Neural Network)-Modell mit dem MNIST-Datensatz für Handschriftzahlen und erklären schrittweise, wie man die wichtigsten Metriken und Daten während des Trainings mithilfe von TensorBoard visualisiert.
Kernvisualisierungselemente:
| Visualisierungstyp | Visualisierte Inhalte | TensorBoard-Tab |
|---|---|---|
| Skalar-Metriken | Trainings-/Testverlust (loss), Trainings-/Testgenauigkeit (accuracy), Lernrate (learning rate), Gradientnormen (norm) | SCALARS |
| Histogramme/Verteilungen | Gewichts- und Gradientverteilungen für alle Schichten (weights, gradients) | DISTRIBUTIONS, HISTOGRAMS |
| Modellstruktur | Berechnungsgraph des MNIST-CNN-Modells | GRAPHS |
| Feature Maps | Feature Maps der Conv1-Schicht, Feature Maps der Conv2-Schicht, Eingangsbildraster, Visualisierung der Conv1-Filter | IMAGES |
| Einbettungen | 32-dimensionale Feature-Vektoren des FC1-Layers, 2D-Visualisierung mit t-SNE, MNIST-Bilderlabels | PROJECTOR |
| Hyperparameter | Batchgröße, Lernrate, Dropout-Rate, Optimiererart, Weight decay, Momentum, Scheduler-Steps/Gamma | HPARAMS |
Visualisierungszyklen:
- Skalare/Histogramme: alle 50 Batches
- Feature Maps/Bilder: alle 50 Batches
- Einbettungen: nach jeder Epoche
- Hyperparameter: zu Beginn und am Ende des Trainings
Code-Beispiel
In diesem Beispiel wird das Paket dld verwendet. Die benötigten Module werden importiert und das Training gestartet. Die Funktion train() trainiert ein CNN-Modell auf dem MNIST-Datensatz mit den standardmäßigen Hyperparametern und protokolliert den Trainingsprozess in TensorBoard. Um Experimente mit anderen Hyperparametern durchzuführen, kann das Argument hparams_dict an die Funktion train() übergeben werden.
Code
# In a notebook cell:
from dldna.chapter_03.train import train
# Run with default hyperparameters
train()
# Run with custom hyperparameters
my_hparams = {
'batch_size': 128,
'learning_rate': 0.01,
'epochs': 8,
}
train(hparams_dict=my_hparams, log_dir='runs/my_custom_run')
# Start TensorBoard (in a separate cell, or from the command line)
# %load_ext tensorboard
# %tensorboard --logdir runsTensorBoard ausführen:
Nachdem das Training abgeschlossen ist, führen Sie im Shell folgenden Befehl aus, um TensorBoard zu starten.
Code
tensorboard --logdir runsIn Ihrem Webbrowser können Sie sich auf http://localhost:6006 verbinden, um das TensorBoard-Dashboard zu sehen.
Sie können bestätigen, dass für jeden Eintrag mehrere Karten erstellt wurden. 
In jedem Eintrag können Sie die Änderungen einzelner Werte und Bilder überprüfen.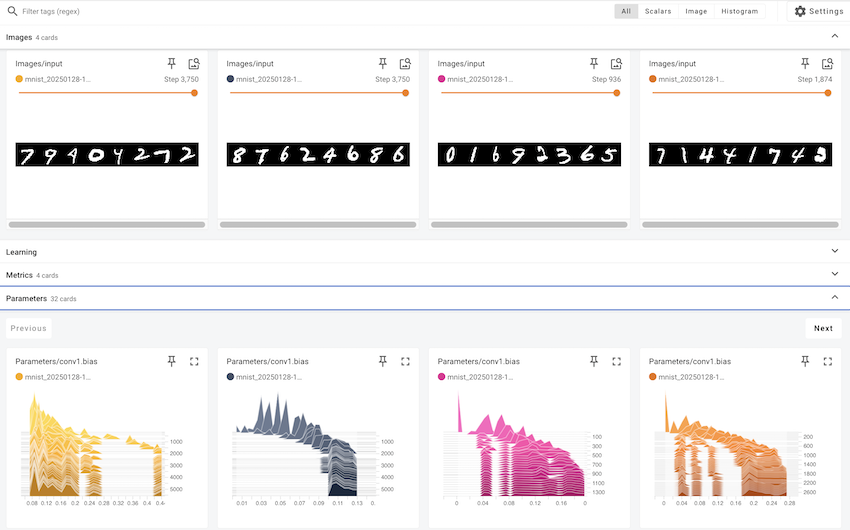 
Verwendung des TensorBoard-Dashboards
- SCALARS-Registerkarte: Verfolgen Sie Änderungen von Trainings-/Testverlust, Genauigkeit, Lernrate usw. im Laufe der Zeit. Dies ermöglicht es Ihnen zu verstehen, ob das Modell gut lernt und ob Overfitting auftritt.
- GRAPHS-Registerkarte: Visualisieren Sie den Berechnungsgraphen des Modells, um den Datenfluss und die Rechenprozesse übersichtlich darzustellen. Dies hilft beim Verstehen der Struktur komplexer Modelle.
- DISTRIBUTIONS/HISTOGRAMS-Registerkarte: Visualisieren Sie die Verteilungen von Gewichten und Gradienten. Dadurch können Sie feststellen, ob die Gewichtsinitialisierung angemessen ist und ob Probleme mit verschwindenden (vanishing gradients) oder explodierenden Gradienten (exploding gradients) vorliegen.
- IMAGES-Registerkarte: Visualisieren Sie Eingangsbilder, Featuremaps, Filter usw. in Form von Bildern. Dadurch können Sie intuitiv erkennen, welche Teile der Bilder das Modell zur Entscheidungsfindung betrachtet und ob die Merkmalsextraktion effektiv ist.
- PROJECTOR-Registerkarte: Projektieren Sie hochdimensionale Einbettungen auf 2D/3D, um sie zu visualisieren. Dadurch können Sie Clustern in den Daten sowie Ausreißer (outliers) identifizieren.
- HPARAMS-Registerkarte: Vergleichen Sie die Ergebnisse von Experimenten mit verschiedenen Hyperparameter-Kombinationen und finden Sie die optimale Konfiguration.
In diesem Beispiel haben wir untersucht, wie man TensorBoard verwendet, um den Trainingsprozess eines Deep-Learning-Modells zu visualisieren. TensorBoard geht über ein einfaches Visualisierungstool hinaus; es ist eine essentielle Werkzeugkiste zum Verständnis des Modellverhaltens, zur Diagnose von Problemen und zur Verbesserung der Leistung.
3.3 Hugging Face Transformers
Hugging Face wurde 2016 von französischen Unternehmern als Chatbot-App für Teenager gegründet. Anfangs hatte es das Ziel, AI-Freunde zu entwickeln, die emotionale Unterstützung und Unterhaltung bieten sollten. Ein großer Wendepunkt kam jedoch, als sie das NLP-Modell ihres Chatbots als Open Source veröffentlichten. Dies fand großen Widerhall in einer Zeit, als hochleistungsfähige Sprachmodelle wie BERT und GPT erschienen, aber ihre praktische Anwendung schwierig war. Die Einführung der Transformers-Bibliothek im Jahr 2019 brachte eine Revolution im Bereich der natürlichen Sprachverarbeitung. Während PyTorch die grundlegenden Berechnungen und das Lernframework für Deep Learning bereitstellte, konzentrierte sich Hugging Face auf die Implementierung und Nutzung tatsächlicher Sprachmodelle. Insbesondere erleichterten sie den Austausch und die Wiederverwendung vortrainierter Modelle, wodurch große Sprachmodelle, die zuvor nur wenigen großen Unternehmen vorbehalten waren, für alle nutzbar wurden.
Hugging Face hat einen offenen Ökosystem aufgebaut, das als “GitHub der KI” bezeichnet werden kann. Aktuell werden über eine Million Modelle und Hunderttausende Datensätze geteilt, was es zu mehr als einem einfachen Code-Repository macht. Es entwickelte sich zu einer Plattform für ethisches und verantwortungsbewusstes KI-Entwicklung. Insbesondere durch die Einführung des Modellkarten-Systems (Model Card) werden die Grenzen und Verzerrungen jedes Modells offen dargelegt, und ein communitybasierter Feedback-Mechanismus stellt sicher, dass die Qualität und Ethik der Modelle kontinuierlich überprüft wird. Diese Anstrengungen gehen über die Demokratisierung der KI-Entwicklung hinaus und legen eine neue Paradigma für verantwortungsbewusste technologische Entwicklung vor. Der Ansatz von Hugging Face behandelt technische Innovationen und ethische Überlegungen gleichermaßen, was es zu einem Vorbild im modernen KI-Entwicklungsprozess gemacht hat.
3.3.1 Einführung in die Transformers-Bibliothek
Transformers bietet eine integrierte Schnittstelle, um vortrainierte Modelle einfach herunterzuladen und zu verwenden. Es funktioniert auf Frameworks wie PyTorch und TensorFlow und stellt so die Kompatibilität mit dem bestehenden Deep-Learning-Ökosystem sicher. Insbesondere unterstützt es auch neue Frameworks wie JAX, was den Auswahlraum für Forscher erweitert. Die Kernkomponenten von Transformers sind in zwei Hauptkategorien unterteilt.
Modellhub und Pipelines
Der Modellhub dient als zentrale Anlaufstelle für vortrainierte Modelle. Es werden spezialisierte Modelle für verschiedene NLP-Aufgaben wie Textgenerierung, Klassifizierung, Übersetzung, Zusammenfassung und Frage- und Antwortstellungen veröffentlicht. Jedes Modell wird mit detaillierten Metadaten wie Leistungsindikatoren, Lizenzinformationen und Herkunft der Trainingsdaten bereitgestellt. Insbesondere durch das System der Modellkarten (Model Card) werden auch die Grenzen und Verzerrungen der Modelle offen dargelegt, um verantwortungsvolle KI-Entwicklung zu fördern.
Die Pipelines abstrahieren komplexe Vorsverarbeitungs- und Nachbearbeitungsprozesse in eine einfache Schnittstelle. Dies ist besonders nützlich im produktiven Einsatz und reduziert die Kosten für die Modellintegration erheblich. Intern konfigurieren Pipelines Tokenizer und Modelle automatisch und führen Optimierungen wie Batch-Verarbeitung oder GPU-Beschleunigung durch.
Code
from transformers import pipeline
classifier = pipeline("sentiment-analysis")
result = classifier("I love this book!")No model was supplied, defaulted to distilbert/distilbert-base-uncased-finetuned-sst-2-english and revision 714eb0f (https://huggingface.co/distilbert/distilbert-base-uncased-finetuned-sst-2-english).
Using a pipeline without specifying a model name and revision in production is not recommended.Device set to use cuda:0Tokenizer und Modellklassen
Der Tokenizer wandelt den Eingabetext in eine numerische Sequenz um, die vom Modell verarbeitet werden kann. Jedes Modell hat seinen eigenen spezifischen Tokenizer, der die Eigenschaften der Trainingsdaten widerspiegelt. Der Tokenizer übernimmt nicht nur einfache Worttrennung, sondern auch komplexe Vorverarbeitungsschritte wie Subword-Tokenisierung, Hinzufügen von Sonderzeichen, Padding und Truncation konsistent. Insbesondere wird die integrierte Unterstützung verschiedener Tokenisierungs-Algorithmen wie WordPiece, BPE, SentencePiece ermöglicht, so dass für jede Sprache und Domäne die optimale Tokenisierungsmethode ausgewählt werden kann.
Die Modellklassen implementieren das neuronale Netzwerk, das die tatsächlichen Berechnungen durchführt. Sie unterstützen verschiedene Architekturen wie BERT, GPT, T5 und ermöglichen über Klassen der AutoModel-Serie die automatische Auswahl der Modellarchitektur. Jedes Modell wird zusammen mit pretrained Gewichten bereitgestellt und kann nach Bedarf für spezifische Aufgaben feinjustiert werden. Zudem können Optimierungstechniken wie Modellparallelisierung, Quantisierung und Pruning direkt angewendet werden.
Code
from transformers import AutoTokenizer, AutoModel
tokenizer = AutoTokenizer.from_pretrained("bert-base-uncased")
model = AutoModel.from_pretrained("bert-base-uncased")3.3.2 Wichtige Anwendungsfälle
Die Transformers-Bibliothek wird für verschiedene Natürlichsprachverarbeitungsaufgaben genutzt. Mit der Entwicklung von GPT-Modellen seit 2020 sind die Fähigkeiten zur Textgenerierung sprunghaft gestiegen, und mit dem Erscheinen hochleistungsfähiger Open-Source-Modelle wie Llama 3 im Jahr 2024 hat sich der Anwendungsbereich weiter erweitert. Insbesondere zeigt das 405B-Parameter-Modell von Llama 3 eine Leistung, die mit GPT-4 vergleichbar ist und in multilinguistischer Verarbeitung, Coding und Inferenzkraft große Fortschritte gemacht hat. Diese Entwicklung ermöglicht vielfältige Anwendungen in realen Geschäftsprozessen. In Bereichen wie Kundensupport, Content-Erstellung, Datenanalyse und automatisierte Prozessabwicklung wird es vielseitig eingesetzt. Besonders die erhebliche Verbesserung der Codeerstellung und -debugging-Fähigkeiten trägt zur Steigerung der Entwicklerproduktivität bei.
Nutzen des Hugging Face Hub:
Der Hugging Face Hub (https://huggingface.co/models) ist eine Plattform, auf der zahlreiche Modelle und Datensätze durchsucht, gefiltert und heruntergeladen werden können.
- Modellsuche: In das Suchfeld in der oberen linken Ecke kann nach Modellnamen (z.B. “bert”, “gpt2”, “t5”) oder Aufgaben (z.B. “text-classification”, “question-answering”) gesucht werden.
- Filtern: Im linken Panel können Modelle nach verschiedenen Kriterien wie Aufgabe (Task), Bibliothek (Libraries), Sprache (Languages) und Datensatz (Datasets) gefiltert werden.
- Modellseite: Jede Modelseite bietet nützliche Informationen, wie Modellbeschreibung, Verwendungsbeispiele, Leistungsindikatoren und Modellkarten.
Textgenerierung und -klassifizierung
Textgenerierung ist die Aufgabe, auf Basis eines gegebenen Prompts natürlichen Text zu erzeugen. Moderne Modelle bieten folgende fortgeschrittene Funktionen: - Multimodale Generierung: Erstellung von Inhalten, die Text und Bilder kombinieren - Automatische Codeerstellung: Schreiben von optimalisierten Codes in verschiedenen Programmiersprachen - Dialogagenten: Implementierung intelligenter Chatbots mit Kontextverständnis - Branchenspezifischer Text: Erstellung spezieller Dokumente in Bereichen wie Medizin und Recht
Code
from transformers import pipeline
# Text generation pipeline (using gpt2 model)
generator = pipeline('text-generation', model='gpt2') # Smaller model
result = generator("Design a webpage that", max_length=50, num_return_sequences=1)
print(result[0]['generated_text'])Device set to use cuda:0
Truncation was not explicitly activated but `max_length` is provided a specific value, please use `truncation=True` to explicitly truncate examples to max length. Defaulting to 'longest_first' truncation strategy. If you encode pairs of sequences (GLUE-style) with the tokenizer you can select this strategy more precisely by providing a specific strategy to `truncation`.
Setting `pad_token_id` to `eos_token_id`:50256 for open-end generation.Design a webpage that is compatible with your browser with our FREE SEO Service.
You read that right. By utilizing a web browser's default settings, your webpage should be free from advertisements and other types of spam. The best way to avoid thisTextklassifizierung wird 2025 weiter verfeinert sein und folgende Funktionen bieten:
- Zero-Shot/Few-Shot Learning: Durch die Hugging Face Transformers-Bibliothek ist eine sofortige Anpassung an neue Kategorien möglich. Insbesondere prägetrainierte Modelle auf Basis von natürlichsprachlicher Inferenz erreichen bei weniger als 8 Beispielen eine Genauigkeit von über 90% und sind in verschiedenen Domains einsetzbar.
- Multilingual Classification: Neuere multilinguale Modelle wie Hugging Face’s ModernBERT unterstützen mehr als 16 Hauptsprachen. Insbesondere das base-Modell mit 150M Parametern erreicht eine F1-Score von über 80% und zeigt auch bei ressourcenarmen Sprachen ausgezeichnete Leistungen.
- Hierarchische Klassifizierung: Hugging Face’s HiGen-Framework bietet spezialisierte Funktionen für die hierarchische Label-Klassifizierung. Durch levelbasierte Verlustfunktionen wird die semantische Beziehung zwischen Text und Label effektiv erfasst, insbesondere bei Klassen mit wenigen Daten.
- Echtzeit-Klassifizierung: Über Hugging Face Pipelines ist die Echtzeit-Verarbeitung von Streaming-Daten möglich. Optimierungstechnologien wie Flash Attention sind standardmäßig integriert und ermöglichen eine effiziente Verarbeitung auch langer Sequenzen, insbesondere in echtzeitkritischen Anwendungen mit hohem Durchsatz.
Feinabstimmung und Modell-Teilen
Hugging Face bietet die neuesten Feinabstimmungstechnologien zur effizienten Lernunterstützung für große Sprachmodelle. Diese Technologien ermöglichen es, die Lernkosten und -zeiten erheblich zu reduzieren, während sie die Leistung des Modells beibehalten.
- QLoRA (Quantized Low-Rank Adaptation): Über Hugging Faces PEFT-Bibliothek zur Verfügung gestellt. Durch die Kombination von 4-Bit Quantisierung und low-rank Anpassung kann der Speicherverbrauch um über 90% reduziert werden. Insbesondere können Modelle mit 65B Parametern auf einem einzelnen 48GB GPU feinjustiert werden.
- Spectrum: Diese Technik zur selektiven Schichtoptimierung ist in die Hugging Face TRL-Bibliothek integriert. Durch die Analyse des Signal-Rausch-Verhältnisses jeder Schicht wird die Berechnungseffizienz verbessert, indem nur wichtige Schichten selektiv trainiert werden.
- Flash Attention: Ab Version 2.2 der Hugging Face Transformers-Bibliothek standardmäßig unterstützt und kann durch den Parameter attn_implementation=“flash_attention_2” leicht aktiviert werden. Insbesondere bei der Verarbeitung langer Sequenzen wird die Speichereffizienz erheblich verbessert.
- DeepSpeed: Vollständig in die Hugging Face Accelerate-Bibliothek integriert und unterstützt durch den ZeRO-Optimierer effizientes großes verteiltes Lernen. Es kann auch während der Inferenz genutzt werden, um große Modelle auf mehreren GPUs zu verteilen.
Code
from transformers import AutoModelForSequenceClassification, AutoTokenizer, TrainingArguments, Trainer, DataCollatorWithPadding
from datasets import Dataset
import torch
import numpy as np
# --- 1. Load a pre-trained model and tokenizer ---
model_name = "distilbert-base-uncased" # Use a small, fast model
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForSequenceClassification.from_pretrained(model_name, num_labels=2) # Binary classification
# --- 2. Create a simple dataset (for demonstration) ---
raw_data = {
"text": [
"This is a positive example!",
"This is a negative example.",
"Another positive one.",
"And a negative one."
],
"label": [1, 0, 1, 0], # 1 for positive, 0 for negative
}
dataset = Dataset.from_dict(raw_data)
# --- 3. Tokenize the dataset ---
def tokenize_function(examples):
return tokenizer(examples["text"], truncation=True) #padding is handled by data collator
tokenized_dataset = dataset.map(tokenize_function, batched=True)
tokenized_dataset = tokenized_dataset.remove_columns(["text"]) # remove text, keep label
# --- 4. Data Collator (for dynamic padding) ---
data_collator = DataCollatorWithPadding(tokenizer=tokenizer)
# --- 5. Training Arguments ---
fp16_enabled = False
if torch.cuda.is_available():
try:
if torch.cuda.get_device_capability()[0] >= 7:
fp16_enabled = True
except:
pass
training_args = TrainingArguments(
output_dir="./results",
num_train_epochs=1, # Keep it short
per_device_train_batch_size=2, # Small batch size
logging_steps=1, # Log every step
save_strategy="no", # No saving
report_to="none", # No reporting
fp16=fp16_enabled, # Use fp16 if avail.
# --- Optimization techniques (demonstration) ---
# gradient_checkpointing=True, # Enable gradient checkpointing (if needed for large models)
# gradient_accumulation_steps=2, # Increase effective batch size
)
# --- 6. Trainer ---
trainer = Trainer(
model=model,
args=training_args,
train_dataset=tokenized_dataset,
# eval_dataset=..., # Add an eval dataset if you have one
data_collator=data_collator, # Use the data collator
# optimizers=(optimizer, scheduler) # you could also customize optimizer
)
# --- 7. Train ---
print("Starting training...")
trainer.train()
print("Training finished!")Some weights of DistilBertForSequenceClassification were not initialized from the model checkpoint at distilbert-base-uncased and are newly initialized: ['classifier.bias', 'classifier.weight', 'pre_classifier.bias', 'pre_classifier.weight']
You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.Starting training.../home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/nn/parallel/_functions.py:71: UserWarning: Was asked to gather along dimension 0, but all input tensors were scalars; will instead unsqueeze and return a vector.
warnings.warn(
[1/1 00:00, Epoch 1/1]
| Step | Training Loss |
|---|---|
| 1 | 0.667500 |
Training finished!Das Modell-Teilecosystem unterstützt derzeit die folgenden neuesten Funktionen bis 2025: - Automatische Erstellung von Modellkarten: Das automatisierte Modellkarten-System von Hugging Face analysiert und dokumentiert Leistungsindikatoren und Verzerrungen automatisch. Insbesondere kann mit dem Model Card Toolkit die Beschreibung der Eigenschaften und Grenzen eines Modells in standardisierter Form klar gegeben werden. - Versionsverwaltung: Das git-basierte Versionsverwaltungssystem des Hugging Face-Hubs verfolgt Änderungshistorien und Leistungsänderungen von Modellen. Es können automatisch Leistungsmetriken und Parameteränderungen pro Version aufgezeichnet und verglichen werden. - Zusammenarbeitstools: Eine integrierte Zusammenarbeitsumgebung durch Hugging Face Spaces wird bereitgestellt. Teammitglieder können Prozesse der Modellentwicklung, -tests und -bereitstellung in Echtzeit teilen und Feedback geben. Es wird auch die Integration mit CI/CD-Pipelines unterstützt. - Ethische KI: Das ethische KI-Framework von Hugging Face überprüft und bewertet die Verzerrungen von Modellen automatisch. Insbesondere können Leistungsunterschiede für verschiedene demografische Gruppen analysiert werden, und potenzielle Risiken im Voraus erkannt werden.
Übungen
1. Grundfragen
- Erklären Sie die Unterschiede zwischen PyTorch-Tensoren und NumPy-Arrays sowie Methoden für ihre gegenseitige Konvertierung.
- Erklären Sie die Rolle des
torch.nn.LinearLayers und Methoden zur Initialisierung der Gewichte. - Erklären Sie, wie automatische Differentiation (automatic differentiation) in PyTorch funktioniert, und beschreiben Sie die Rolle der Eigenschaft
requires_grad.
2. Anwendungsfragen
- Schreiben Sie einen Code, um ein gegebenes Dataset mit
torch.utils.data.Datasetundtorch.utils.data.DataLoaderzu teilen für das Training, die Validierung und den Test, und laden Sie Daten in Batches. - Implementieren Sie ein einfaches CNN-Modell (z.B. LeNet-5) durch Ableitung von
nn.Module, und verwenden Sietorchsummary, um die Struktur des Modells und die Anzahl der Parameter zu überprüfen. - Trainieren Sie das Modell mit dem MNIST- oder Fashion-MNIST-Dataset, und visualisieren Sie den Trainingsprozess (Verlust, Genauigkeit usw.) mithilfe von TensorBoard.
3. Fortgeschrittene Fragen
- Implementieren Sie Matrixmultiplikation, Transposition, Batch-Matrixmultiplikation, bilineare Transformationen etc. mit
torch.einsum. (Stellen Sie die Einsteinsche Summenkonvention für jede Operation dar und implementieren Sie sie in PyTorch-Code.) - Schreiben Sie einen Code, um ein benutzerdefiniertes Dataset zu erstellen und Datenverstärkung (data augmentation) mit
torchvision.transformsanzuwenden. (Beispiel: Bildrotation, -ausschneiden, Farbänderungen usw.) - Erklären Sie die Methode zur Berechnung höherer Ableitungen (higher-order derivatives) mit
torch.autograd.grad, und schreiben Sie ein einfaches Beispielcode. (Beispiel: Berechnung der Hesse-Matrix) - Erklären Sie, warum das Aufrufen der
forward()-Methode vontorch.nn.Moduledirekt vermieden wird und stattdessen das Modellobjekt wie eine Funktion aufgerufen wird. (Hinweis: Beziehen Sie sich auf die__call__-Methode und den Zusammenhang mit dem System der automatischen Differentiation)
Klicken Sie hier, um den Inhalt anzuzeigen (Lösung)
Übungslösungen
1. Lösungen zu grundlegenden Aufgaben
- Tensor vs. NumPy-Array:
- Unterschiede: Tensoren unterstützen GPU-Beschleunigung und automatisches Differenzieren. NumPy bietet CPU-basierte allgemeine Array-Operationen.
- Konvertierung:
torch.from_numpy(),.numpy()(für GPU-Tensoren vorher.cpu()).
# Beispiel import torch import numpy as np numpy_array = np.array([1, 2, 3]) torch_tensor = torch.from_numpy(numpy_array) # oder torch.tensor() numpy_back = torch_tensor.cpu().numpy() nn.Linear:- Funktion:
y = xW^T + b(lineare Transformation). Multipliziert den Eingabewertxmit dem GewichtWund addiert den Biasb. - Initialisierung: Standardmäßig Kaiming He-Initialisierung (gleichmäßige Verteilung). Änderbar durch das Modul
torch.nn.init.
# Beispiel import torch.nn as nn import torch.nn.init as init linear_layer = nn.Linear(in_features=10, out_features=5) init.xavier_uniform_(linear_layer.weight) # Xavier-Initialisierung- Funktion:
- Automatisches Differenzieren (Autograd):
- Funktionsweise: Wenn
requires_grad=Truefür Tensoren gilt, wird ein Berechnungsgraph erstellt und bei Aufruf von.backward()werden die Gradienten durch Anwendung der Kettenregel berechnet. requires_grad: Legt fest, ob Gradienten berechnet und verfolgt werden sollen.
# Beispiel import torch x = torch.tensor([2.0], requires_grad=True) y = x**2 + 3*x + 1 y.backward() print(x.grad) # Ausgabe: tensor([7.]) - Funktionsweise: Wenn
2. Lösungen zu anwendungsbezogenen Aufgaben
Dataset,DataLoader:from torch.utils.data import Dataset, DataLoader, random_split import torchvision.transforms as transforms from torchvision import datasets # Custom Dataset (Beispiel) class CustomDataset(Dataset): def __init__(self, data, targets, transform=None): self.data = data self.targets = targets self.transform = transform def __len__(self): return len(self.data) def __getitem__(self, idx): sample, label = self.data[idx], self.targets[idx] if self.transform: sample = self.transform(sample) return sample, labelMNIST DataLoader Beispiel (mit torchvision)
transform = transforms.ToTensor() # Bildendaten in Tensoren umwandeln mnist_dataset = datasets.MNIST(root=‘./data’, train=True, download=True, transform=transform) train_size = int(0.8 * len(mnist_dataset)) val_size = len(mnist_dataset) - train_size train_dataset, val_dataset = random_split(mnist_dataset, [train_size, val_size]) train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True) val_loader = DataLoader(val_dataset, batch_size=32)
5. **LeNet-5, `torchsummary`, TensorBoard:** (Der gesamte Code ist in der vorherigen Antwort zu finden, hier nur die Kernpunkte)
```python
import torch.nn as nn
import torch.nn.functional as F
from torchsummary import summary
from torch.utils.tensorboard import SummaryWriter
# LeNet-5 Modell
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=2)
self.pool1 = nn.AvgPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5, stride=1)
self.pool2 = nn.AvgPool2d(kernel_size=2, stride=2)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.relu(self.conv1(x))
x = self.pool1(x)
x = F.relu(self.conv2(x))
x = self.pool2(x)
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
model = LeNet5()
summary(model, input_size=(1, 28, 28)) # Zusammenfassung der Modellstruktur
# ... (Trainingscode, siehe vorherige Antwort) ...
writer = SummaryWriter() # TensorBoard
# ... (Während des Trainings Logging mit writer.add_scalar() etc.) ...
writer.close()3. Erweiterte Übungen Lösungen
torch.einsum:
import torchA = torch.randn(3, 4) B = torch.randn(4, 5) C = torch.einsum(“ij,jk->ik”, A, B) # Matrixmultiplikation D = torch.einsum(“ij->ji”, A) # Transposition E = torch.einsum(“bi,bj,ijk->bk”, A, B, torch.randn(2,3,4)) # Bilineare Transformation
7. **Benutzerdefinierte Datensätze, Datenverstärkung:**
```python
from torch.utils.data import Dataset
from torchvision import transforms
from PIL import Image
import os
class CustomImageDataset(Dataset): # Erbt von Dataset
def __init__(self, root_dir, transform=None):
# ... (Konstruktor-Implementierung) ...
pass
def __len__(self):
# ... (Anzahl der Daten zurückgeben) ...
pass
def __getitem__(self, idx):
# ... (Stichprobe für den angegebenen Index zurückgeben) ...
pass
# Datenverstärkung
transform = transforms.Compose([
transforms.RandomResizedCrop(224), # Zufälliges Crop in Größe und Verhältnis
transforms.RandomHorizontalFlip(), # Horizontales Spiegeln
transforms.ToTensor(), # In Tensor umwandeln
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) # Normalisierung
])
# dataset = CustomImageDataset(root_dir='path/to/images', transform=transform)- Höhere Ableitungen:
import torch
x = torch.tensor(2.0, requires_grad=True)
y = x**3
# Erste Ableitung
first_derivative = torch.autograd.grad(y, x, create_graph=True)[0] # create_graph=True
print(first_derivative)
# Zweite Ableitung (Hesse-Matrix)
second_derivative = torch.autograd.grad(first_derivative, x)[0]
print(second_derivative)__call__Methode:
Die __call__ Methode von nn.Module führt zusätzliche Aufgaben (wie Hook-Registrierung, Einstellungen zur automatischen Differentiation) vor und nach dem Aufruf von forward() aus. Ein direkter Aufruf von forward() kann diese Funktionen überspringen, was zu fehlerhaften Gradientenberechnungen oder einem nicht ordnungsgemäßen Betrieb anderer Funktionalitäten (z.B. die Einstellung des training-Attributs in nn.Module) führen kann. Daher muss das Modellobjekt immer wie eine Funktion aufgerufen werden (model(input)).
Referenzmaterialien
- PyTorch-Offizielles Tutorial: https://pytorch.org/tutorials/
- Deep Learning with PyTorch (Stevens, Antiga, Viehmann, 2020): https://pytorch.org/deep-learning-with-pytorch
- Programming PyTorch for Deep Learning (Delugach, 2023): https://www.oreilly.com/library/view/programming-pytorch-for/9781098142481/
- PyTorch Recipes (Kalyan, 2019): https://pytorch.org/tutorials/recipes/recipes_index.html
- Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
- Fastai-Bibliothek: https://docs.fast.ai/
- PyTorch Lightning: https://www.pytorchlightning.ai/
- Hugging Face Transformers-Dokumentation: https://huggingface.co/docs/transformers/index
- TensorBoard-Dokumentation: https://www.tensorflow.org/tensorboard
- Weights & Biases-Dokumentation: https://docs.wandb.ai/