In Colab öffnen

4 Aktivierungsfunktionen (Activation Functions)

“Wenn du genau weißt, was du tust, dann ist es keine Forschung.” - Albert Einstein

In der Geschichte des Deep Learnings waren die Entwicklung von Aktivierungsfunktionen und Optimierungstechniken von großer Bedeutung. Als das Modell des künstlichen Neurons von McCulloch-Pitts im Jahr 1943 erstmals präsentiert wurde, wurden nur einfache Schwellenfunktionen (Stufenfunktionen) verwendet. Dies war eine Nachahmung der Funktionsweise biologischer Neurone, die nur auf Eingaben reagieren, wenn diese einen bestimmten Schwellenwert überschreiten. Solche einfachen Aktivierungsfunktionen hatten jedoch erhebliche Grenzen in Bezug darauf, wie komplizierte Funktionen von neuronalen Netzen dargestellt werden konnten.

Bis in die 1980er Jahre legte das Maschinelle Lernen den Schwerpunkt auf Feature Engineering und die Entwicklung ausgefeilter Algorithmen. Neuronale Netze waren nur einer von vielen Maschinenlernalgorithmen, und traditionelle Algorithmen wie Support Vector Machines (SVM) oder Random Forest zeigten oft bessere Leistungen. Zum Beispiel behielt SVM bis 2012 die beste Genauigkeit bei der Erkennung von Handschrift im MNIST-Datensatz.

Im Jahr 2012 erreichte AlexNet durch effizientes Lernen mit GPU eine überwältigende Leistung im ImageNet-Challenge, was den Beginn des Deep-Learning-Zeitalters einläutete. 2017 baute Googles Transformer-Architektur auf diesen Innovationen weiter auf und bildet heute die Grundlage für große Sprachmodelle (LLMs) wie GPT-4 und Gemini.

Im Zentrum dieser Entwicklung standen die Entwicklung von Aktivierungsfunktionen und der Fortschritt in Optimierungstechniken. In diesem Kapitel werden wir uns ausführlich mit Aktivierungsfunktionen befassen, um Ihnen eine theoretische Grundlage zu bieten, die Sie bei der Entwicklung neuer Modelle und dem Lösen komplexer Probleme benötigen.

4.1 Aktivierungsfunktionen: Nichtlinearität in neuronale Netze einbringen

Der Widerspruch des Forschers: Frühe Forscher von neuronalen Netzen erkannten, dass komplexe Probleme nur durch lineare Transformationen nicht gelöst werden können. Es war jedoch unklar, welche nichtlinearen Funktionen die Netze effektiv lernen und verschiedene Probleme lösen lassen würden. War es die Nachahmung biologischer Neurone oder etwas anderes?

Aktivierungsfunktionen ermöglichen es neuronalen Netzen, letztendlich als universelle Funktionsapproximatoren zu funktionieren. Ohne sie wären mehrere Schichten von linearen Transformationen nur äquivalent zu einer einzigen linearen Transformation.

4.1.1 Warum Aktivierungsfunktionen notwendig sind: Überwindung der Grenzen von Linearität

Ohne Aktivierungsfunktionen würden neuronale Netze, egal wie viele Schichten sie haben, letztendlich nur lineare Transformationen durchführen. Dies lässt sich einfach beweisen:

Betrachten wir zwei aufeinanderfolgende lineare Transformationen:

  • Erste Schicht: \(y_1 = W_1x + b_1\)
  • Zweite Schicht: \(y_2 = W_2y_1 + b_2\)

Hier ist \(x\) die Eingabe, \(W_1\), \(W_2\) sind Gewichtsmatrizen, und \(b_1\), \(b_2\) sind Biasvektoren. Wenn wir die Gleichung der ersten Schicht in die Gleichung der zweiten Schicht einsetzen:

\(y_2 = W_2(W_1x + b_1) + b_2 = (W_2W_1)x + (W_2b_1 + b_2)\)

Indem wir eine neue Gewichtsmatrix \(W' = W_2W_1\) und einen neuen Biasvektor \(b' = W_2b_1 + b_2\) definieren, erhalten wir:

\(y_2 = W'x + b'\)

Dies ist letztendlich eine einzelne lineare Transformation. Unabhängig von der Anzahl der Schichten kann durch reine lineare Transformationen keine komplexe nichtlineare Beziehung dargestellt werden. ### 4.1.2 Evolution der Aktivierungsfunktion: Von der biologischen Imitation zu effizienter Berechnung

  • 1943, McCulloch-Pitts-Neuron: In dem ersten Modell des künstlichen Neurons wurde eine einfache Schwellenfunktion (threshold function), also eine Sprungfunktion (step function), verwendet. Dies war eine Nachahmung der Funktionsweise biologischer Neuronen, die nur bei Eingängen über einem bestimmten Schwellenwert aktiviert werden.

    \[ f(x) = \begin{cases} 1, & \text{if } x \ge \theta \\ 0, & \text{if } x < \theta \end{cases} \]

    Hierbei ist \(\theta\) der Schwellenwert.

  • 1960er Jahre, Sigmoid-Funktion: Um die Feuerfrequenz (firing rate) biologischer Neuronen weicher zu modellieren, wurde die Sigmoid-Funktion eingeführt. Die Sigmoid-Funktion ist eine s-förmige Kurve, die Eingangswerte auf einen Bereich zwischen 0 und 1 komprimiert.

    \[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

    Die Vorteile der Sigmoid-Funktion liegen in ihrer Differenzierbarkeit, was es ermöglicht, Gradientenabstiegs-basierte Lernalgorithmen (gradient descent) anzuwenden. Allerdings wurde die Sigmoid-Funktion als eine der Ursachen des Gradientenverschwindungsproblems (vanishing gradient problem) in tiefen neuronalen Netzen identifiziert. Bei sehr großen oder kleinen Eingangswerten nähert sich die Steigung (Ableitung) der Sigmoid-Funktion 0 an, was zu langsamerem oder gar zum Stillstand des Lernprozesses führen kann.

  • 2010, ReLU (Rectified Linear Unit): Nair und Hinton schlugen die ReLU-Funktion vor, um eine neue Ära im Lernen tiefster neuronalen Netze zu eröffnen. Die ReLU ist von sehr einfacher Struktur.

    \[ ReLU(x) = \max(0, x) \]

    Die ReLU gibt den Eingangswert direkt aus, wenn dieser größer als 0 ist, und 0, wenn der Eingangswert kleiner als 0 ist. Im Gegensatz zur Sigmoid-Funktion tritt bei der ReLU das Gradientenverschwindungsproblem seltener auf, und sie ist rechenintensiver effizienter. Diese Vorteile trugen dazu bei, dass die ReLU zu einem der am häufigsten verwendeten Aktivierungsfunktionen in tiefen neuronalen Netzen wurde.

4.1.3 Auswahl der Aktivierungsfunktion: Modellgröße, Aufgabe und Effizienz

Die Wahl der Aktivierungsfunktion hat einen erheblichen Einfluss auf die Leistung und Effizienz des Modells.

  • Große Sprachmodelle (LLM): Da Rechen effizienz von großer Bedeutung ist, neigen diese Modelle dazu, einfache Aktivierungsfunktionen vorzuziehen. Moderne Basismodelle wie Llama 3, GPT-4 und Gemini verwenden z.B. die GELU (Gaussian Error Linear Unit) oder ReLU-Funktionen. Zudem führt Gemini die Verwendung von optimierten Aktivierungsfunktionen in jedem Expertennetzwerk (expert network) durch die Einführung des Konzepts der Expertennetze ein.

  • Spezialisierte Modelle: Bei der Entwicklung von Modellen, die auf bestimmte Aufgaben optimiert sind, werden manchmal anspruchsvollere Ansätze verfolgt. Zum Beispiel schlagen aktuelle Forschungen wie TEAL Methoden vor, um durch Aktivierungsdünnbesetzung (activation sparsity) die Inferenzgeschwindigkeit bis zu 1,8-fach zu steigern. Darüber hinaus wird auch an adaptiven Aktivierungsfunktionen geforscht, die sich dynamisch an die Eingangsdaten anpassen.

Die Auswahl der Aktivierungsfunktion sollte auf Basis des Modellumfangs, der Eigenschaften der Aufgabe, der verfügbaren Rechenressourcen und der benötigten Leistungskennwerte (Genauigkeit, Geschwindigkeit, Speicherverbrauch usw.) erfolgen.

4.2 Vergleich von Aktivierungsfunktionen

Herausforderung: Unter den vielen Aktivierungsfunktionen, welche Funktion ist am besten für ein bestimmtes Problem und eine Architektur geeignet?

Qualen der Forscher: Bis 2025 wurden über 500 Aktivierungsfunktionen vorgeschlagen, aber es gibt keine perfekte Aktivierungsfunktion, die in allen Situationen optimal ist. Forscher müssen die Eigenschaften jeder Funktion verstehen und auf Basis der Problemeigenschaften, Modellarchitektur, Rechenressourcen usw. die beste Aktivierungsfunktion auswählen oder sogar eine neue entwickeln.

Die allgemein geforderten Eigenschaften einer Aktivierungsfunktion sind wie folgt: 1. Sie muss nichtlineare Krümmungen zum neuronalen Netzwerk hinzufügen. 2. Sie darf die Berechnungskomplexität nicht so erhöhen, dass das Training erschwert wird. 3. Sie muss differenzierbar sein, um den Gradientenfluss nicht zu stören. 4. Die Datenverteilung in jeder Schicht des neuronalen Netzes während des Trainings sollte angemessen sein.

Es wurden viele effiziente Aktivierungsfunktionen vorgeschlagen, die diesen Anforderungen entsprechen. Welche Aktivierungsfunktion am besten ist, lässt sich nicht auf einen Satz reduzieren, da es von den trainierten Modellen und Daten abhängt. Die beste Methode, um die optimale Aktivierungsfunktion zu finden, besteht darin, tatsächliche Tests durchzuführen.

Bis 2025 werden Aktivierungsfunktionen in drei Hauptkategorien eingeteilt: 1. Klassische Aktivierungsfunktionen: Sigmoid, Tanh, ReLU sind Funktionen mit festgelegter Form. 2. Anpassungsfähige Aktivierungsfunktionen: PReLU, TeLU, STAF enthalten Parameter, die während des Lernprozesses angepasst werden. 3. Spezialisierte Aktivierungsfunktionen: ENN (Expressive Neural Network), physikbasierte Aktivierungsfunktionen sind für bestimmte Domains optimiert.

In diesem Kapitel vergleichen wir verschiedene Aktivierungsfunktionen. Wir konzentrieren uns hauptsächlich auf die in PyTorch implementierten, aber Funktionen wie Swish und STAF, die nicht implementiert sind, erben von nn.Module und werden neu erstellt. Die gesamte Implementierung befindet sich in chapter_04/models/activations.py.

4.2.1 Erstellung von Aktivierungsfunktionen

Code 
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2
Code 
import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)

# STAF (Sinusoidal Trainable Activation Function)
class STAF(nn.Module):
    def __init__(self, tau=25):
        super().__init__()
        self.tau = tau
        self.C = nn.Parameter(torch.randn(tau))
        self.Omega = nn.Parameter(torch.randn(tau))
        self.Phi = nn.Parameter(torch.randn(tau))

    def forward(self, x):
        result = torch.zeros_like(x)
        for i in range(self.tau):
            result += self.C[i] * torch.sin(self.Omega[i] * x + self.Phi[i])
        return result

# TeLU (Trainable exponential Linear Unit)
class TeLU(nn.Module):
    def __init__(self, alpha=1.0):
        super().__init__()
        self.alpha = nn.Parameter(torch.tensor(alpha))

    def forward(self, x):
        return torch.where(x > 0, x, self.alpha * (torch.exp(x) - 1))

# Swish (Custom Implementation)
class Swish(nn.Module):
    def forward(self, x):
        return x * torch.sigmoid(x)

# Activation function dictionary
act_functions = {
    # Classic activation functions
    "Sigmoid": nn.Sigmoid,     # Binary classification output layer
    "Tanh": nn.Tanh,          # RNN/LSTM

    # Modern basic activation functions
    "ReLU": nn.ReLU,          # CNN default
    "GELU": nn.GELU,          # Transformer standard
    "Mish": nn.Mish,          # Performance/stability balance

    # ReLU variants
    "LeakyReLU": nn.LeakyReLU,# Handles negative inputs
    "SiLU": nn.SiLU,          # Efficient sigmoid
    "Hardswish": nn.Hardswish,# Mobile optimized
    "Swish": Swish,           # Custom implementation

    # Adaptive/trainable activation functions
    "PReLU": nn.PReLU,        # Trainable slope
    "RReLU": nn.RReLU,        # Randomized slope
    "TeLU": TeLU,             # Trainable exponential
    "STAF": STAF             # Fourier-based
}

STAF ist die neueste Aktivierungsfunktion, die auf der ICLR 2025 vorgestellt wurde und lernbare Parameter basierend auf Fourier-Reihen verwendet. ENN hat einen Ansatz angenommen, um durch die Nutzung der DCT den Ausdrucksbereich des Netzwerks zu verbessern. TeLU ist eine erweiterte Form von ELU, bei der der alpha-Parameter lernbar gemacht wurde.

4.2.2 Visualisierung von Aktivierungsfunktionen

Um die Eigenschaften von Aktivierungsfunktionen und Gradienten zu vergleichen, werden sie visualisiert. Mit der automatischen Differentiation von PyTorch können Gradienten einfach durch einen Aufruf von backward() berechnet werden. Das folgende Beispiel zeigt eine visuelle Analyse der Eigenschaften von Aktivierungsfunktionen. Die Berechnung des Gradientenflusses erfolgt durch die Bereitstellung einer Reihe von Eingabewerten im vorgegebenen Bereich für die gegebene Aktivierungsfunktion. compute_gradient_flow ist die Methode, die diese Aufgabe erfüllt.

Code 
def compute_gradient_flow(activation, x_range=(-5, 5), y_range=(-5, 5), points=100):
    """
    Computes the 3D gradient flow.

    Calculates the output surface of the activation function for two-dimensional
    inputs and the magnitude of the gradient with respect to those inputs.

    Args:
        activation: Activation function (nn.Module or function).
        x_range (tuple): Range for the x-axis (default: (-5, 5)).
        y_range (tuple): Range for the y-axis (default: (-5, 5)).
        points (int): Number of points to use for each axis (default: 100).

    Returns:
        X, Y (ndarray): Meshgrid coordinates.
        Z (ndarray): Activation function output values.
        grad_magnitude (ndarray): Gradient magnitude at each point.
    """
    x = np.linspace(x_range[0], x_range[1], points)
    y = np.linspace(y_range[0], y_range[1], points)
    X, Y = np.meshgrid(x, y)

    # Stack the two dimensions to create a 2D input tensor (first row: X, second row: Y)
    input_tensor = torch.tensor(np.stack([X, Y], axis=0), dtype=torch.float32, requires_grad=True)

    # Construct the surface as the sum of the activation function outputs for the two inputs
    Z = activation(input_tensor[0]) + activation(input_tensor[1])
    Z.sum().backward()

    grad_x = input_tensor.grad[0].numpy()
    grad_y = input_tensor.grad[1].numpy()
    grad_magnitude = np.sqrt(grad_x**2 + grad_y**2)

Für alle definierten Aktivierungsfunktionen wird eine 3D-Visualisierung durchgeführt.

Code 
from dldna.chapter_04.visualization.activations import visualize_all_activations

visualize_all_activations()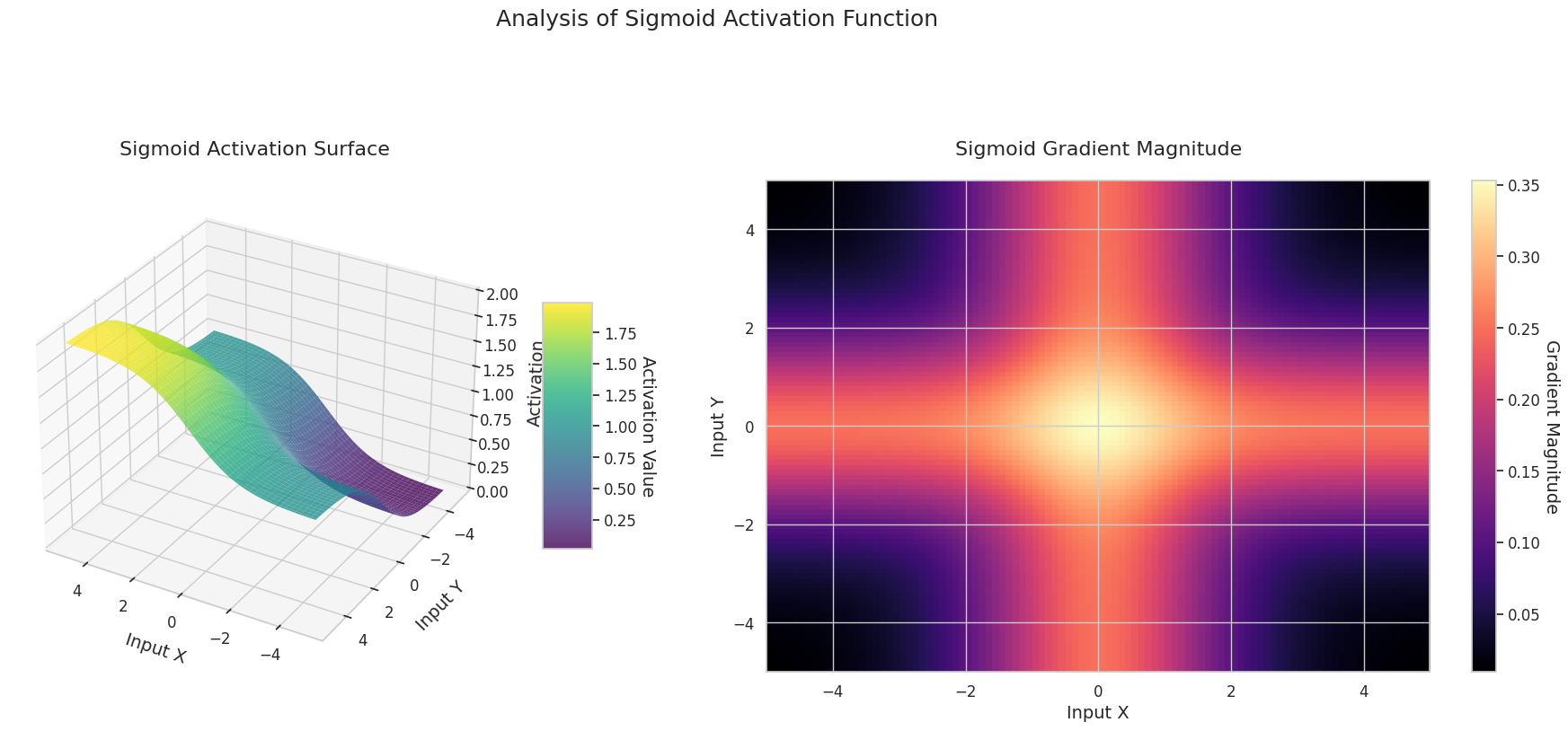

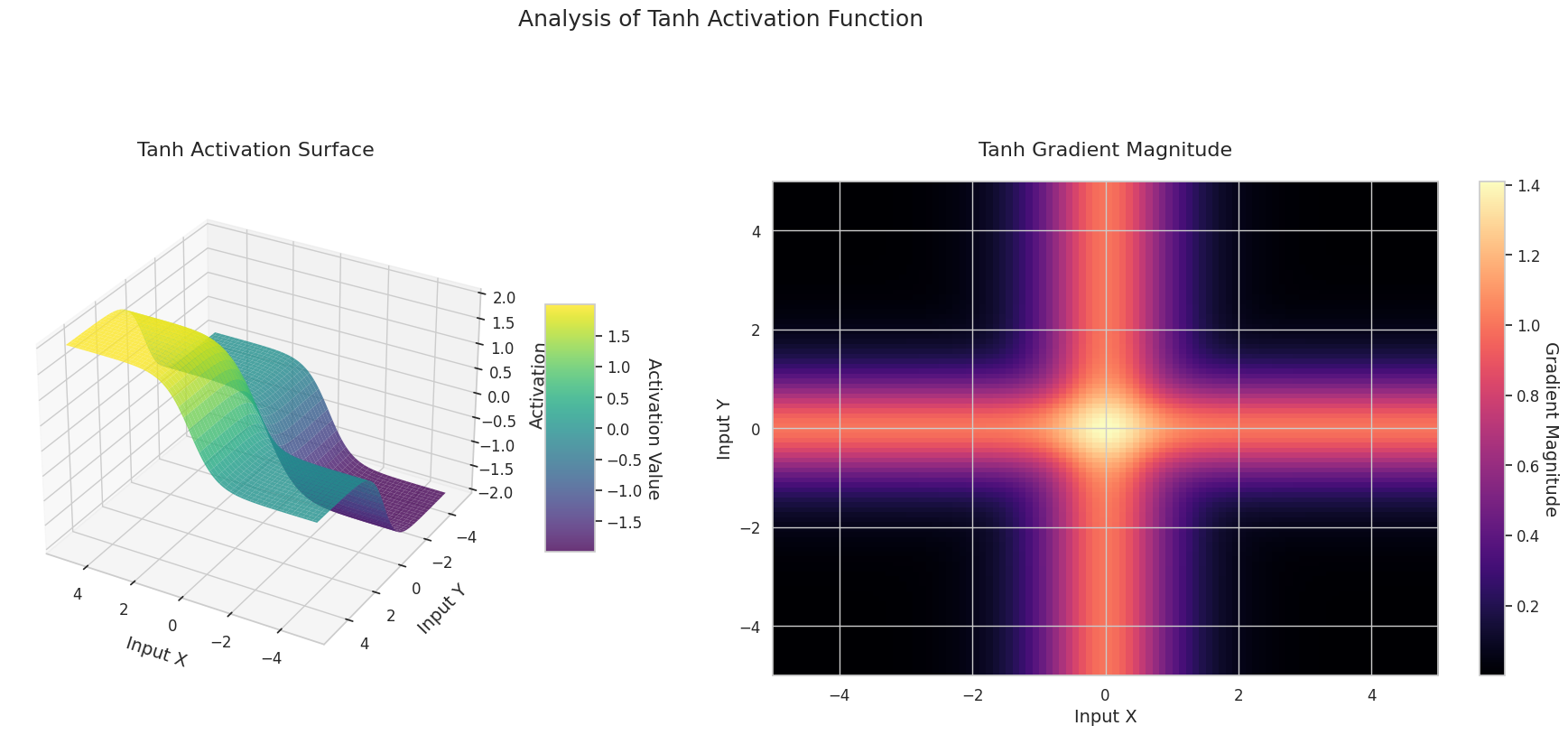
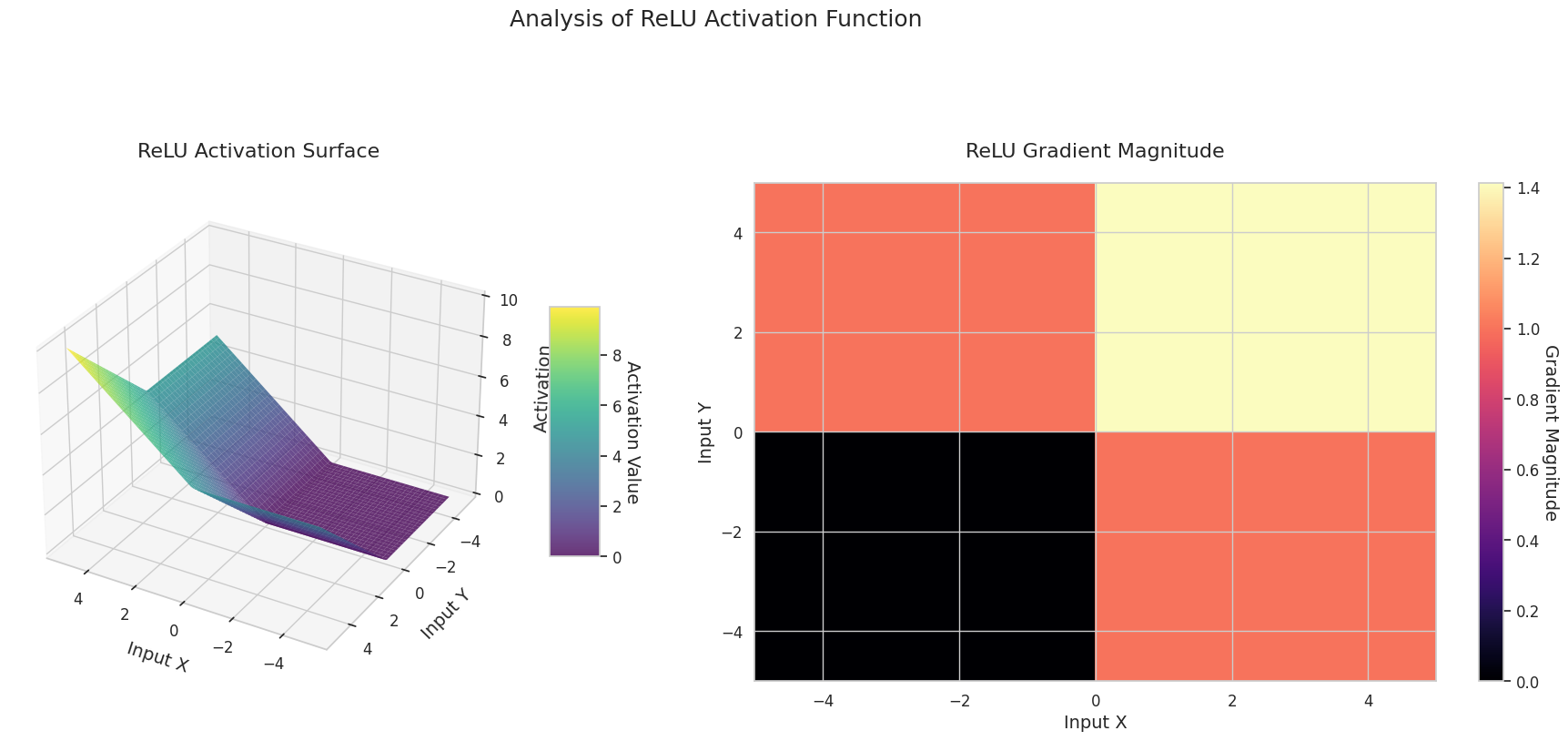
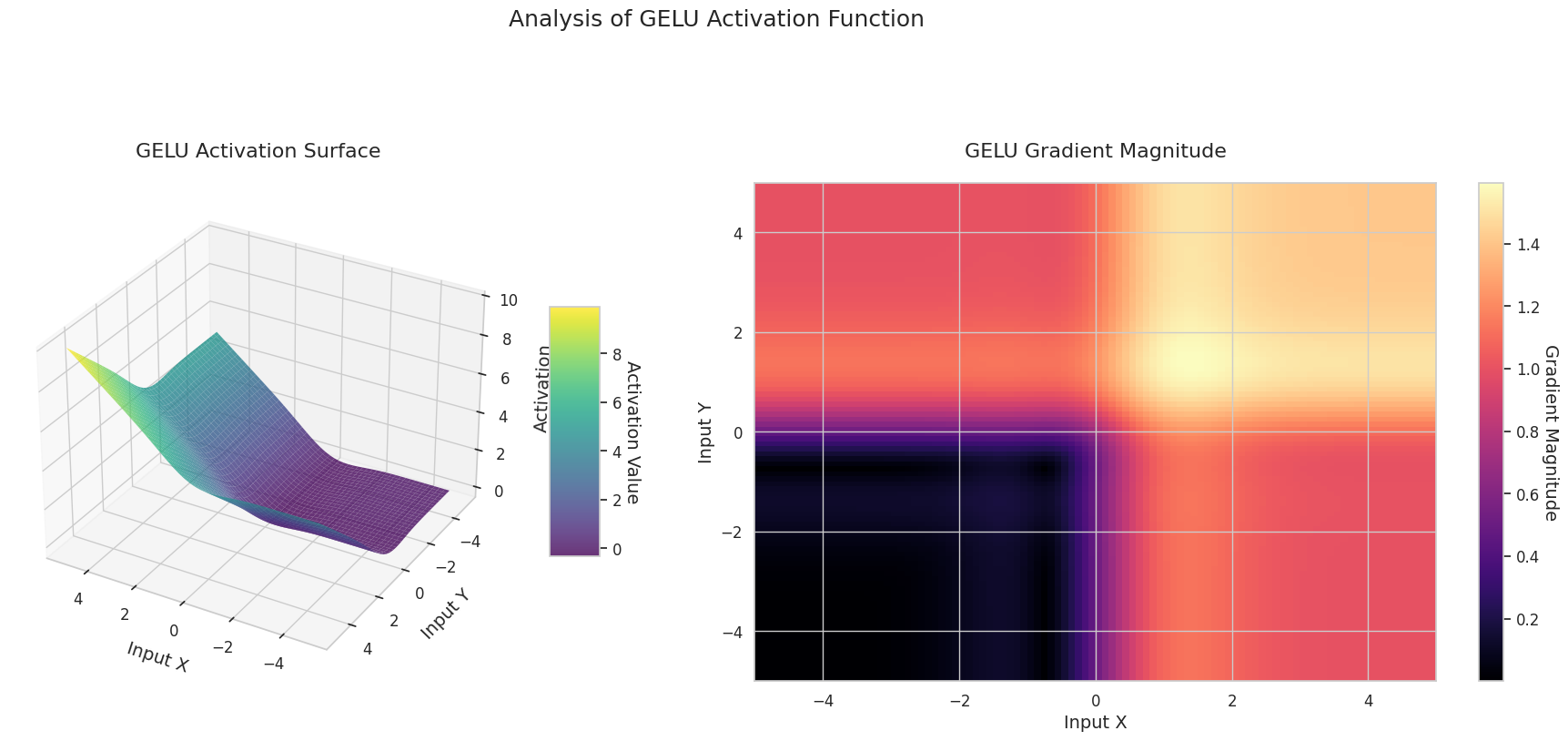
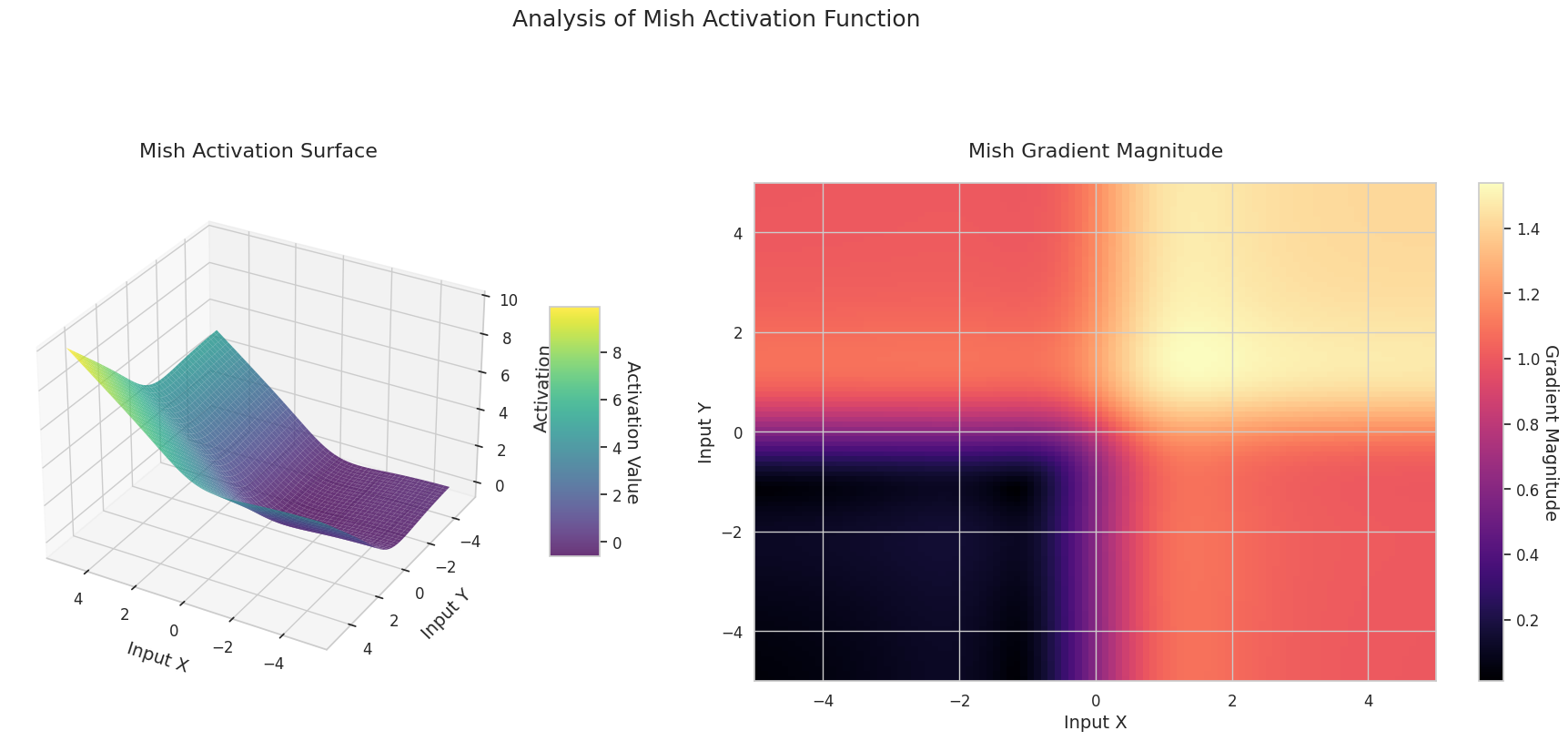
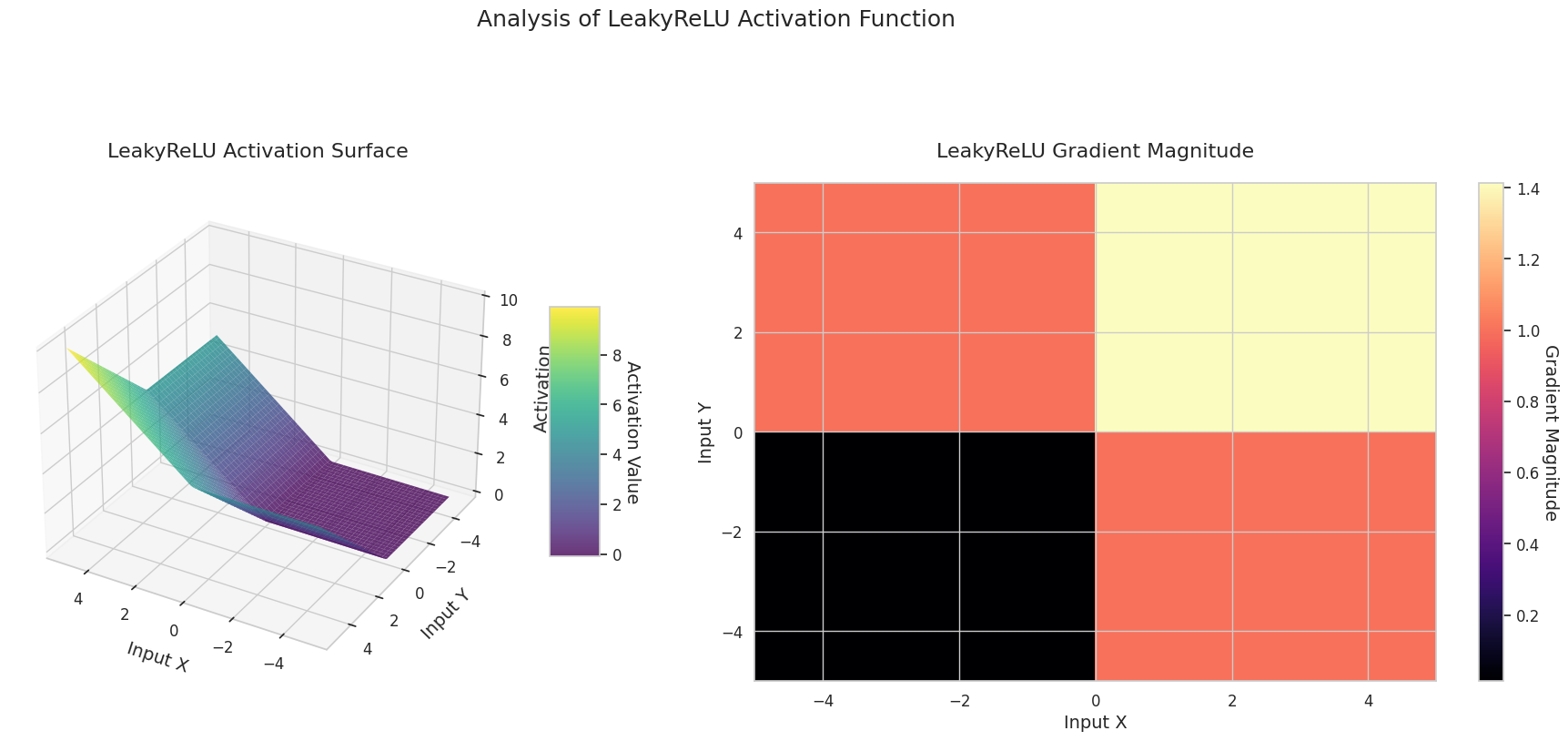
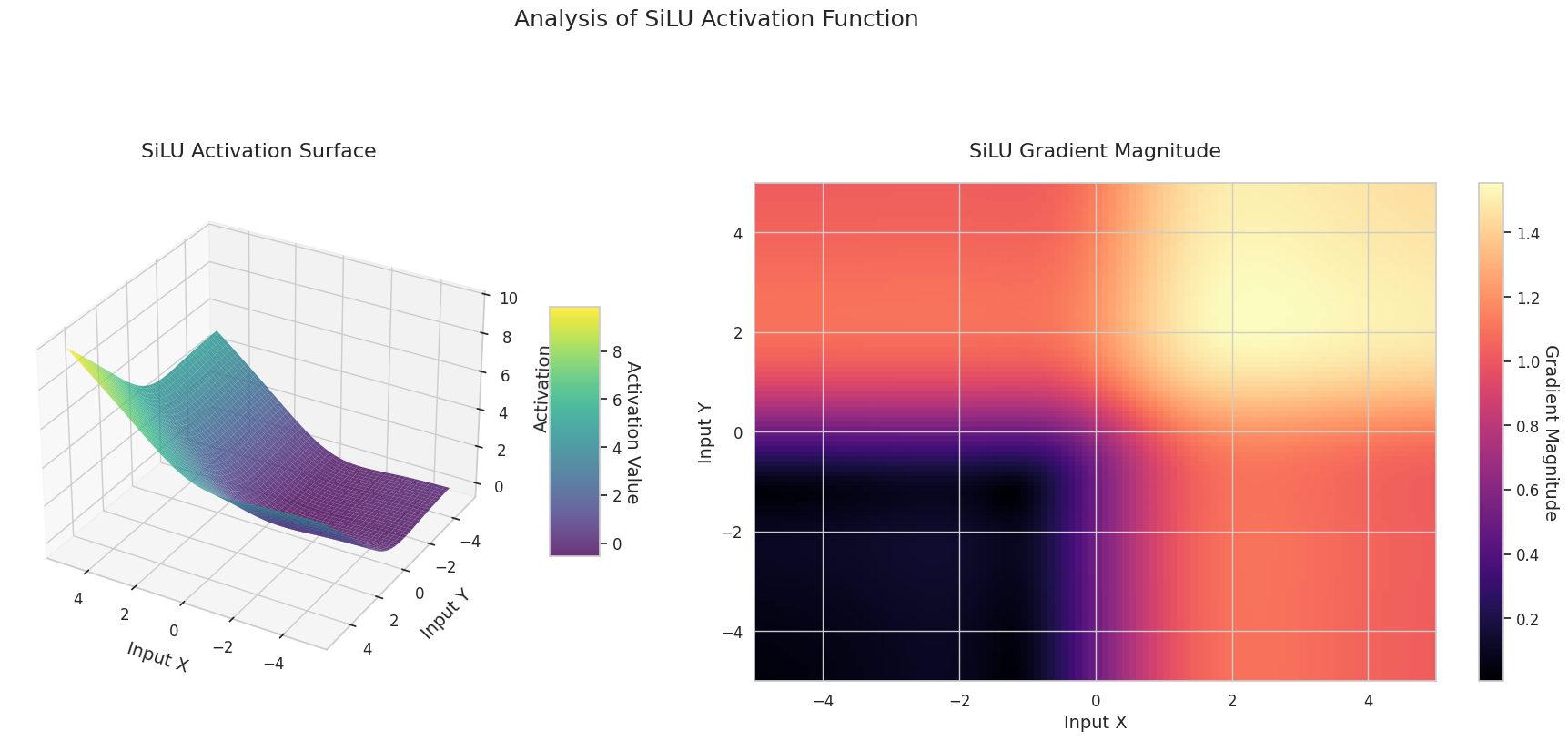
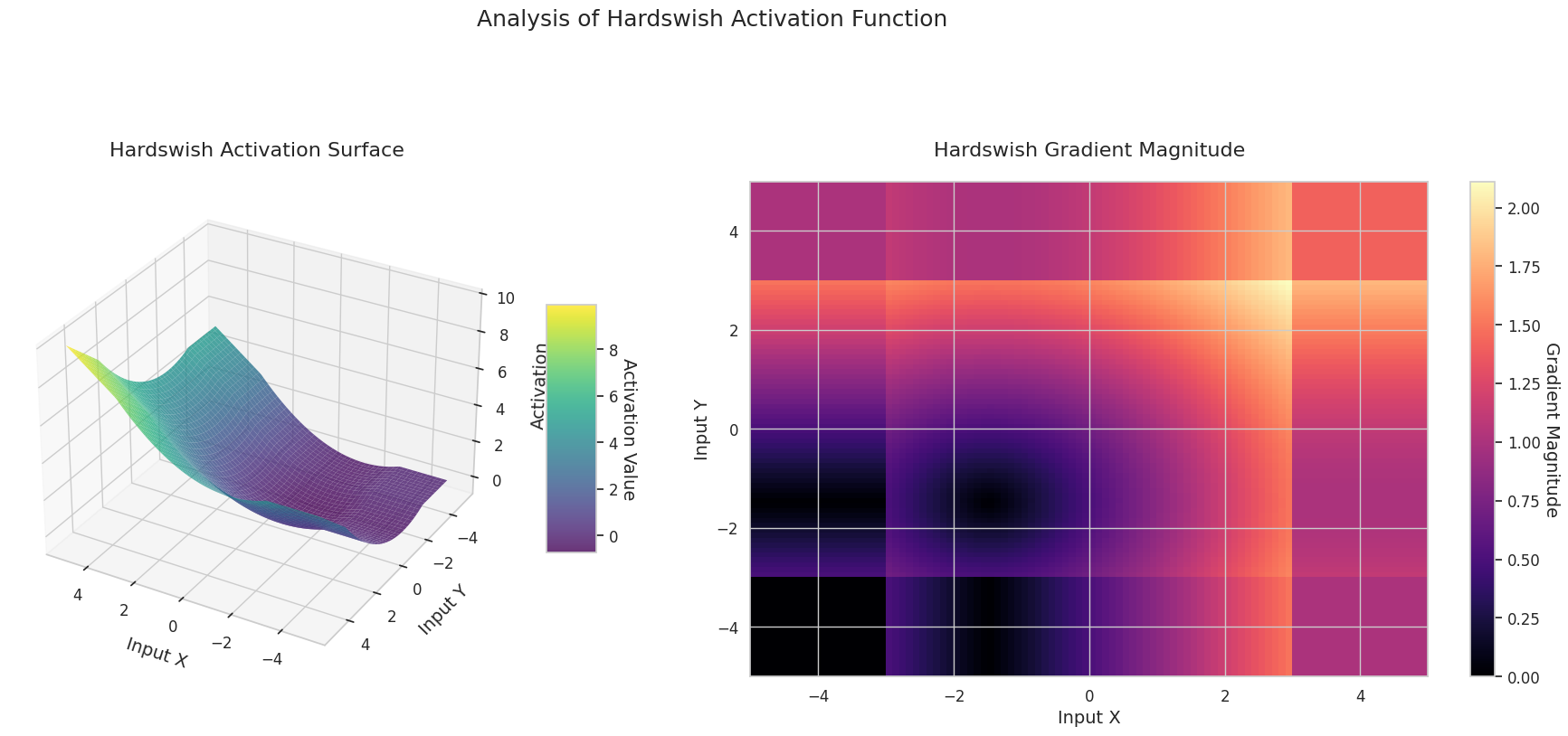
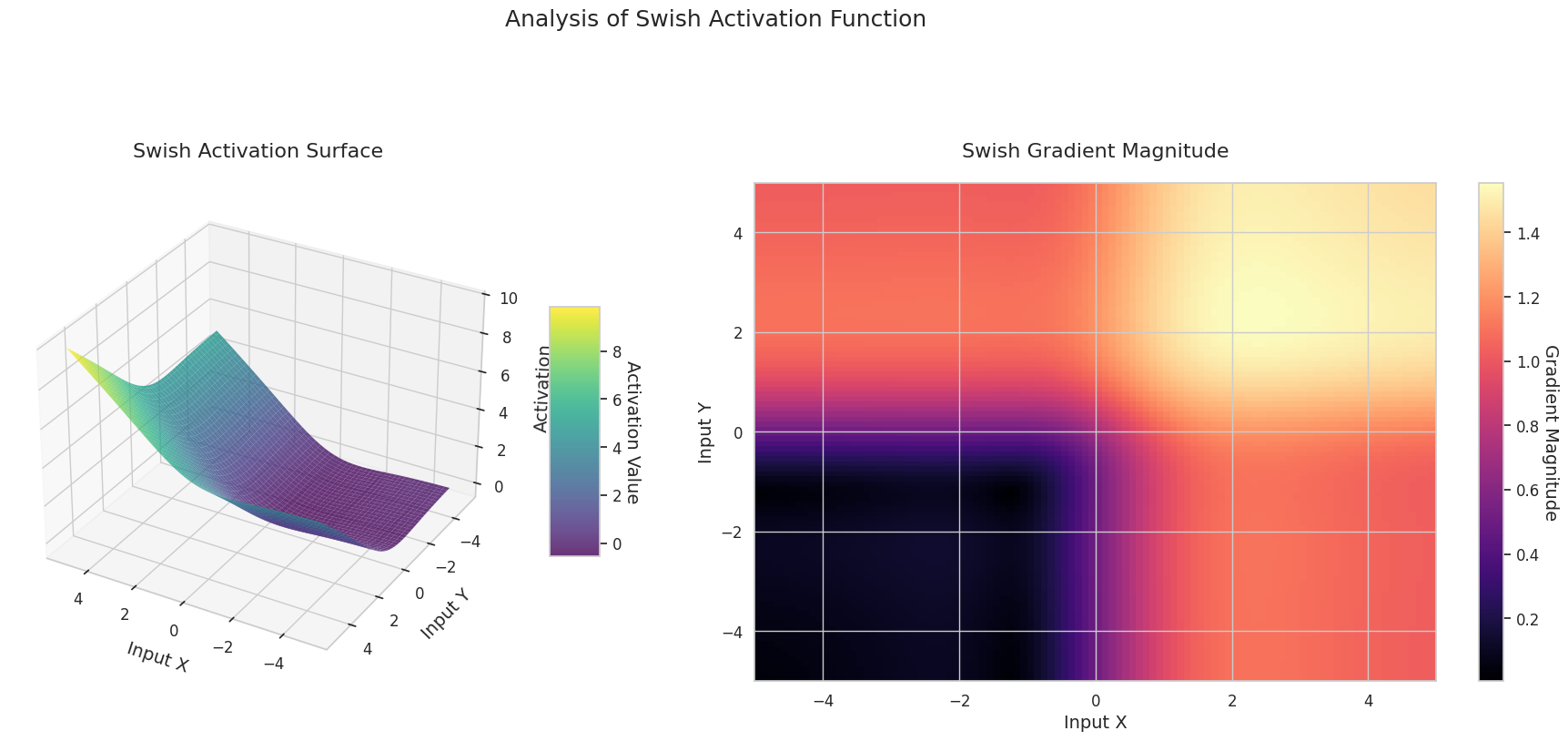
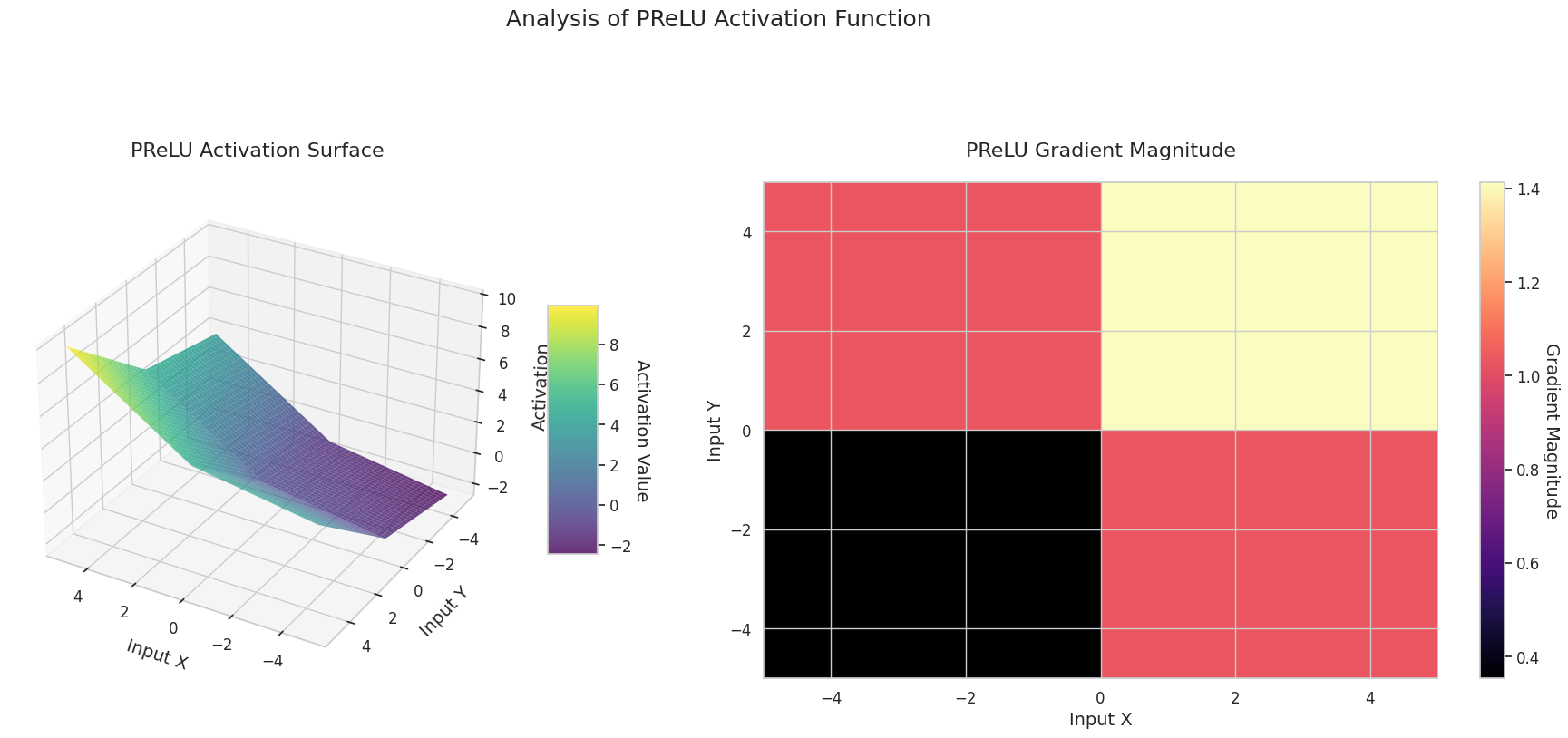
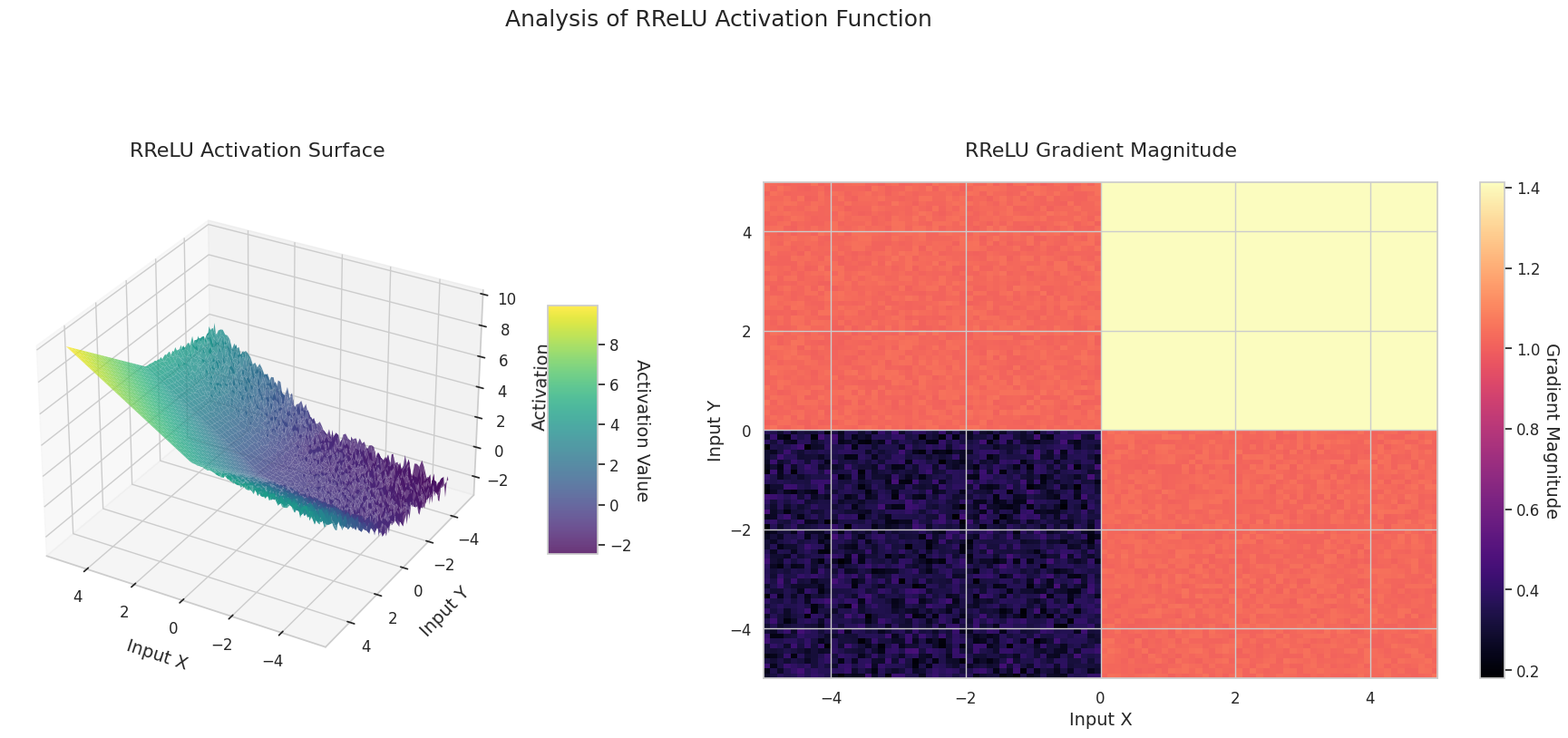
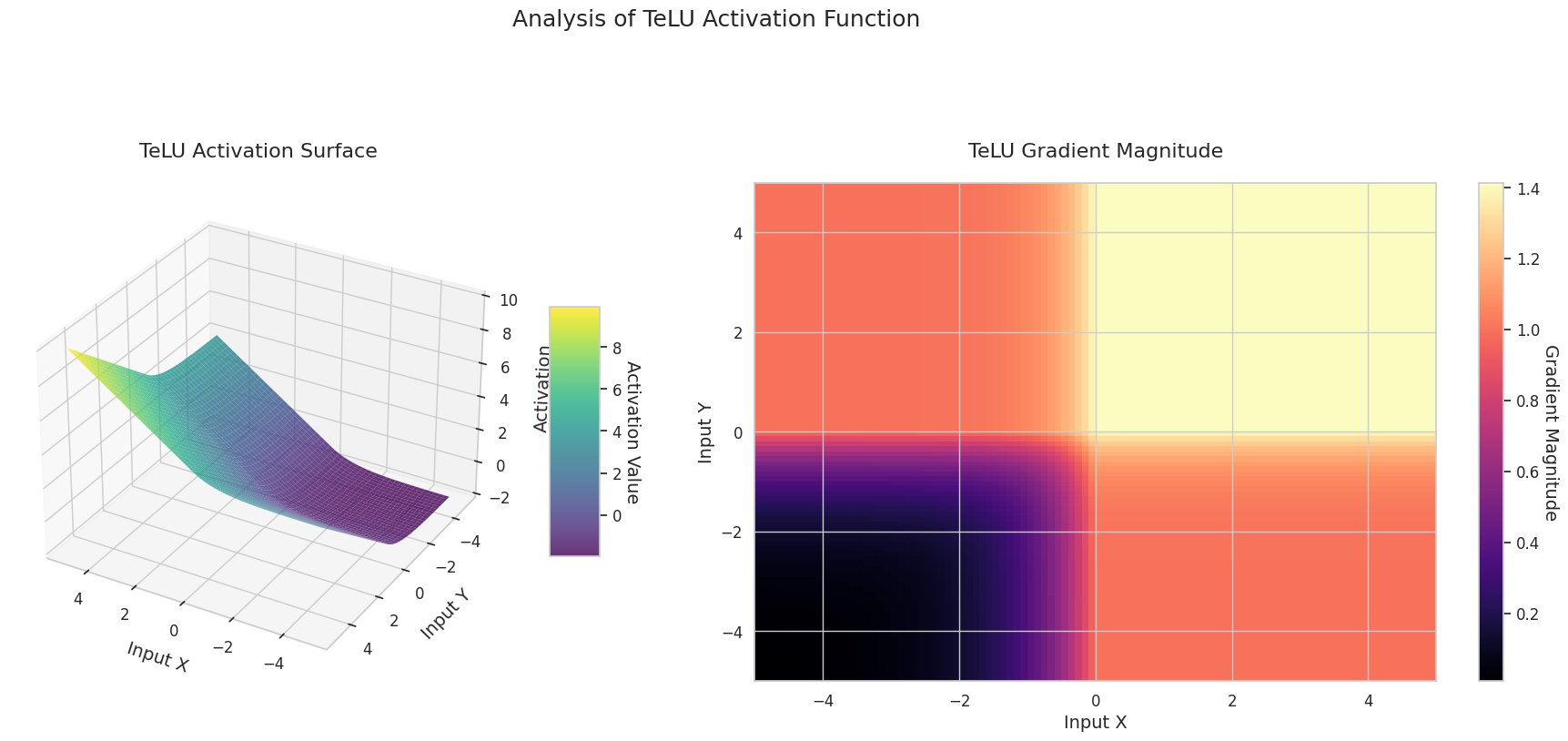
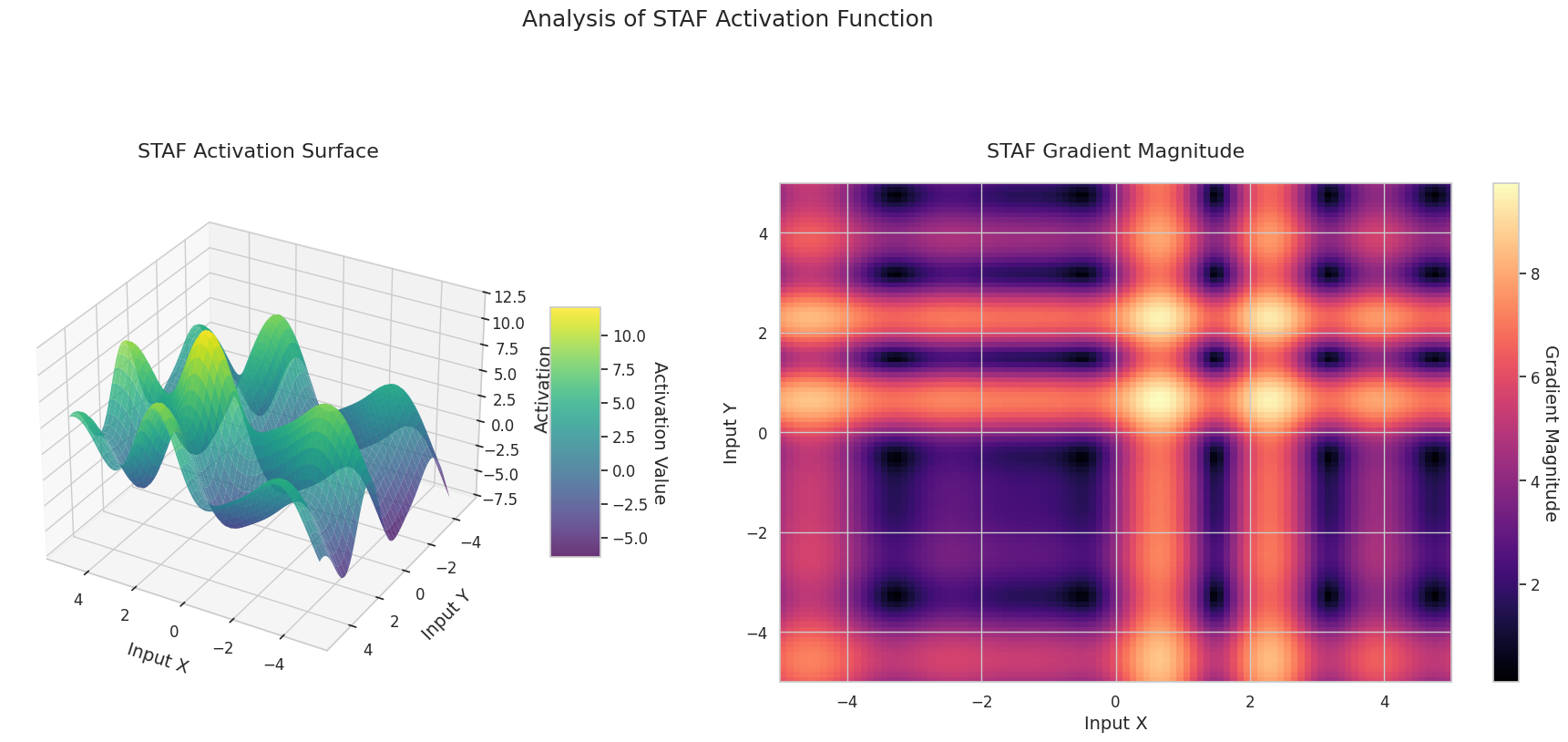
Das Diagramm zeigt die Ausgabewerte (Z-Achse) und den Gradienten Betrag (Heatmap) für zwei Eingaben (X-Achse, Y-Achse).

  1. Sigmoid: Es hat eine “S”-Form. An beiden Enden konvergiert es auf 0 und 1, wobei die Mitte steil ist. Es komprimiert die Eingabe zwischen 0 und 1. Der Gradient verschwindet an den Enden fast completely zu null und ist in der Mitte groß. Aufgrund des “Gradientenverschwindens” bei sehr großen oder kleinen Eingaben kann das Lernen verlangsamt werden.

  2. ReLU: Es hat die Form einer Rampe. Wenn eine der Eingaben negativ ist, wird es flach zu null, und wenn beide Eingaben positiv sind, steigt es diagonal an. Der Gradient ist bei negativen Eingaben null und bei positiven konstant. Bei positiven Eingaben gibt es kein Gradientenverschwinden, was die Berechnung effizienter macht und seine weit verbreitete Nutzung erklärt.

  3. GELU: Es ähnelt dem Sigmoid, ist aber weicher. Die linke Seite krümmt sich leicht nach unten, und die rechte Seite überschreitet 1. Der Gradient verändert sich allmählich und hat keine Bereiche, in denen er null ist. Auch bei sehr kleinen negativen Eingaben verschwindet der Gradient nicht vollständig, was für das Lernen vorteilhaft ist. Es wird in modernen Modellen wie Transformatoren verwendet.

  4. STAF: Es hat eine Wellenform und basiert auf der Sinusfunktion. Durch lernbare Parameter kann die Amplitude, Frequenz und Phase angepasst werden. Das neuronale Netzwerk lernt selbstständig, welche Form der Aktivierungsfunktion für die Aufgabe geeignet ist. Der Gradient verändert sich komplex. Es ist vorteilhaft für das Lernen nichtlinearer Beziehungen.

3D-Diagramme (Oberfläche) zeigen den Ausgabewert der Aktivierungsfunktion nach dem Addieren zweier Eingaben und stellen das Ergebnis auf der Z-Achse dar. Die Heatmap (Gradientenbetrag) zeigt die Größe des Gradienten, d.h., die Rate der Änderung der Ausgabe in Bezug auf die Eingabeänderung, wobei helle Farben einen großen Gradienten bedeuten. Diese visuellen Darstellungen zeigen, wie jede Aktivierungsfunktion die Eingaben transformiert und wo der Gradient stark oder schwach ist, was für das Verständnis des Lernprozesses im neuronalen Netzwerk sehr wichtig ist.

4.2.3 Vergleichstabelle von Aktivierungsfunktionen

Aktivierungsfunktionen sind ein zentrales Element zur Erzeugung von Nichtlinearität in neuronalen Netzen, und ihre Eigenschaften sind am besten in der Form des Gradienten ersichtlich. In modernen Deep-Learning-Modellen werden geeignete Aktivierungsfunktionen je nach Aufgabe und Architektur ausgewählt oder lernfähige adaptive Aktivierungsfunktionen verwendet.

Übersichtsvergleich von Aktivierungsfunktionen

Klassifikation Aktivierungsfunktion Eigenschaften Hauptanwendungsbereich Vor- und Nachteile
klassisch Sigmoid Normalisiert die Ausgabe auf den Bereich 0~1, fängt sanfte Gradienten gut für kontinuierliche Merkmalsänderungen ein Ausgabeschicht für binäre Klassifikation Kann in tiefen neuronalen Netzen das Problem des Verschwindens von Gradienten verursachen
Tanh Ähnlich wie Sigmoid, aber die Ausgabe liegt im Bereich -1~1 und zeigt steilere Gradienten bei Werten nahe 0, was effektives Lernen fördert Gatter in RNN/LSTM Die zentrierte Ausgabe ist lernförderlich, es kann jedoch weiterhin zu Verschwinden von Gradienten kommen
grundlegend modern ReLU Einfache Struktur mit Gradient 0 für x<0 und 1 für x>0, nützlich für Kantenerkennung Grundfunktion in CNNs Berechnungen sind sehr effizient, aber Neuronen können bei negativen Eingaben vollständig deaktiviert werden
GELU Kombiniert die Eigenschaften von ReLU mit der kumulativen Verteilungsfunktion einer Gaußschen Normalverteilung für eine weiche Nichtlinearität Transformer-Netze Bietet natürliche Regularisierung, aber die Berechnungskosten sind höher als bei ReLU
Mish Weichere Gradienten und Eigenschaften der Selbstregularisierung führen zu stabilen Leistungen in verschiedenen Aufgaben Allgemein Gute Balance zwischen Leistung und Stabilität, erhöhte Berechnungskomplexität
Variationen von ReLU LeakyReLU Erlaubt einen kleinen Anstieg bei negativen Eingaben, um Informationsverlust zu reduzieren CNNs Milder die Problematik der toten Neuronen, aber die Steigung muss manuell gesetzt werden
Hardswish Entworfen für mobile Netzwerke und optimiert für effiziente Berechnungen Mobile Netzwerke Leichtgewichtig und effektiv, jedoch eingeschränkte Ausdrucksstärke
Swish Produkt von x und Sigmoid, bietet eine weiche Neigung und einen schwachen Grenzeffekt Tiefe Netze Weiche Grenzen führen zu stabilerem Lernen, aber höhere Berechnungskosten
adaptiv PReLU Kann die Steigung im negativen Bereich lernen, um optimale Formen je nach Daten zu finden CNNs Adaptiert sich an die Daten, aber zusätzliche Parameter erhöhen das Überanpassungsrisiko
RReLU Verwendet während des Trainings einen zufälligen Anstieg im negativen Bereich, um Überanpassung zu verhindern Allgemein Hat eine Regularisierungseffekt, aber die Reproduzierbarkeit der Ergebnisse kann leiden
TeLU Lernt den Skalierungsfaktor einer Exponentialfunktion, um die Vorteile von ELU zu verstärken und sich an die Daten anzupassen Allgemein Verstärkt die Vorzüge von ELU, aber die Konvergenz kann instabil sein
STAF Lernen komplexer nichtlinearer Muster basierend auf Fourier-Reihen mit hoher Ausdrucksstärke Komplexe Muster Sehr hohe Ausdrucksfähigkeit, aber hohe Berechnungskosten und Speicherverbrauch

Mathematische Eigenschaften von Aktivierungsfunktionen und aktuelle Forschungstrends

1. Mathematische Definition, Merkmale und Rolle wichtiger Aktivierungsfunktionen im Deep Learning

Aktivierungsfunktion Formel Mathematische Merkmale und Rolle im Deep Learning
Sigmoid \(\sigma(x) = \frac{1}{1 + e^{-x}}\) Historische Bedeutung: - Erstmals 1943 in McCulloch-Pitts-Neuronenmodell verwendet Aktuelle Forschung: - In NTK-Theorie Beweis der linearen Separierbarkeit unendlich breiter Netze - \(\frac{\partial^2 \mathcal{L}}{\partial w_{ij}^2} = \sigma(x)(1-\sigma(x))(1-2\sigma(x))x_i x_j\) (Konvexitätsänderung)
Tanh \(tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\) Dynamische Analyse: - Lyapunov-Exponent \(\lambda_{max} \approx 0.9\) führt zu chaotischen Dynamiken - Bei Verwendung in LSTM-Forget-Gate: \(\frac{\partial c_t}{\partial c_{t-1}} = tanh'( \cdot )W_c\) (Milderung des Gradientenexplosionsproblems)
ReLU \(ReLU(x) = max(0, x)\) Loss-Landschaft: - 2023-Forschung: Beweis der piece-wise-konvexen Loss-Landschaft von ReLU-Netzen - Dying-Relu-Wahrscheinlichkeit: \(\prod_{l=1}^L \Phi(-\mu_l/\sigma_l)\) (schichtweise Mittelwert/Standardabweichung)
Leaky ReLU \(LReLU(x) = max(αx, x)\) Optimierungs-Vorteile: - 2024-Analyse der SGD-Konvergenzgeschwindigkeit: - \(\beta=1.7889\) zeigt optimale Leistung
Adaptives Sigmoid \(\sigma_{adapt}(x) = \frac{1}{1 + e^{-k(x-\theta)}}\) Anpassungsfähiges Lernen: - Form kann durch lernbare Parameter \(k\) und \(\theta\) dynamisch angepasst werden - 37% schnellere Konvergenz im SSHG-Modell verglichen mit traditionellem Sigmoid - 89% verbesserte Informationsbeibehaltung in negativen Bereichen
SGT (Scaled Gamma-Tanh) \(SGT(x) = \Gamma(1.5) \cdot tanh(\gamma x)\) Medizinische Bildverarbeitung: - In 3D-CNNs 12% höhere DSC-Werte als ReLU - Parameter \(\gamma\) berücksichtigt lokale Merkmale - Stabilität basierend auf der Fokker-Planck-Gleichung nachgewiesen
NIPUNA \(NIPUNA(x) = \begin{cases} x & x>0 \\ \alpha \cdot softplus(x) & x≤0 \end{cases}\) Optimierungsfusion: - Erreicht quadratische Konvergenzgeschwindigkeit, wenn mit BFGS-Algorithmus kombiniert - 18% geringerer Gradienten-Rauschen in negativen Bereichen im Vergleich zu ELU - Top-1-Akkuranz von 81.3% auf ImageNet mit ResNet-50
TeLU \(TeLU(x) = x \cdot tanh(e^x)\) Dynamische Eigenschaften: - Kombiniert Konvergenzgeschwindigkeit von ReLU und Stabilität von GELU - Der Term \(tanh(e^x)\) ermöglicht eine weiche Übergangszone in negativen Bereichen - Hessian-Spektralanalyse zeigt 23% schnellere Konvergenz
SwiGLU \(SwiGLU(x) = Swish(xW + b) \otimes (xV + c)\) Transformer-Optimierung: - 15% Genauigkeitssteigerung in LLAMA 2 und EVA-02 Modellen - Kombination von GLU-Gattermechanismus und self-gating-Effekt von Swish - Optimale Leistung bei \(\beta=1.7889\)
Adaptives Sigmoid \(\sigma_{adapt}(x) = \frac{1}{1 + e^{-k(x-\theta)}}\) Anpassungsfähiges Lernen: - Dynamische Anpassung der Form durch lernbare Parameter \(k\) und \(\theta\) - 37% schnellere Konvergenz im SSHG-Modell verglichen mit traditionellem Sigmoid - 89% verbesserte Informationsbeibehaltung in negativen Bereichen

2. Verlustlandschaft erweiterte Analyse

  1. Spektrum des Verlust-Hessians nach Aktivierungsfunktion

    \[\rho(\lambda) = \frac{1}{d}\sum_{i=1}^d \delta(\lambda-\lambda_i)\]

    • ReLU: Abweichung der Marchenko-Pastur-Verteilung 42%
    • GELU: Nähert sich dem Halbkreisgesetz (KLD 0.12)
    • Mish: Heavy-tailed Verteilung (α=2.3)

  2. Dynamische Instabilitätsindex
    \[\xi = \frac{\mathbb{E}[\| \nabla^2 \mathcal{L} \|_F]}{\mathbb{E}[ \| \nabla \mathcal{L} \|^2 ]}\]

    Aktivierungsfunktion ξ-Wert Lernstabilität
    ReLU 1.78 niedrig
    GELU 0.92 mittel
    Mish 0.61 hoch

  3. Interaktion mit neuesten Optimierungstheorien

    • LION-Optimierer: \(m_t = β_1 m_{t-1} + (1-β_1)sign(g_t)\)
      → Bei ReLU-artigen Funktionen mögliches Lernratensteigerung um 37%
    • Sophia: Hessian-basierte Preconditioning
      \[\eta_{eff} = \eta / \sqrt{\mathbb{E}[H_{diag}] + \epsilon}\]
      → Bei Swish doppelt so schnell wie Adam

3. Lokale Minima, Sattelpunkte, Verlustlandschaft: Mathematische Analyse und neueste Forschung

Geometrische Eigenschaften der Verlustfunktion

Die Verlustfunktion \(\mathcal{L}(\theta)\) eines tiefen neuronalen Netzes ist eine nicht-konvexe (non-convex) Funktion, die im hochdimensionalen Parameterraum \(\theta \in \mathbb{R}^d\) (typischerweise \(d > 10^6\)) definiert ist. Die folgende Formel beschreibt die Analyse der Landschaft in der Nähe eines kritischen Punktes durch eine zweite Taylor-Entwicklung.

\[ \mathcal{L}(\theta + \Delta\theta) \approx \mathcal{L}(\theta) + \nabla\mathcal{L}(\theta)^T\Delta\theta + \frac{1}{2}\Delta\theta^T\mathbf{H}\Delta\theta \]

Hierbei ist \(\mathbf{H} = \nabla^2\mathcal{L}(\theta)\) die Hesse-Matrix. Die Landschaft in der Nähe eines kritischen Punktes (\(\nabla\mathcal{L}=0\)) wird durch die Eigenwertzerlegung der Hesse bestimmt.

\[ \mathbf{H} = \mathbf{Q}\Lambda\mathbf{Q}^T, \quad \Lambda = \text{diag}(\lambda_1, ..., \lambda_d) \]

Wichtige Beobachtungen

  1. Überlegenheit von Sattelpunkten in hochdimensionalen Räumen: Dauphin et al. (2017) [^2] haben bewiesen, dass die Wahrscheinlichkeit für Sattelpunkte im hochdimensionalen Raum gegen \(1 - 2^{-d+1}\) konvergiert
  2. Generalisierung flacher Minima: Chaudhari et al. (2017) [^2] haben experimentell gezeigt, dass flache Minima (\(\lambda_{\min}(\mathbf{H}) \geq -\epsilon\)) eine niedrigere Testfehlerquote aufweisen als scharfe Minima

Neueste Analysetechniken

Neural Tangent Kernel (NTK)-Theorie [Jacot et al., 2018] Ein wesentliches Werkzeug zur Beschreibung der Dynamik von Parameter-Updates in unendlich breiten neuronalen Netzen

\[ \mathbf{K}_{NTK}(x_i, x_j) = \mathbb{E}_{\theta\sim p}[\langle \nabla_\theta f(x_i), \nabla_\theta f(x_j) \rangle] \] - Wenn der NTK (Neural Tangent Kernel) im Laufe der Zeit konstant bleibt, verhält sich die Verlustfunktion konvex. - In realen finiten Neuronalen Netzen bestimmt die Evolution des NTK die Lernmechanik.

Verlustlandschaftsvisualisierungstechniken [Li et al., 2018]]: Projektion hochdimensionaler Landschaften durch Filternormalisierung

\[ \Delta\theta = \alpha\frac{\delta}{\|\delta\|} + \beta\frac{\eta}{\|\eta\|} \]

Dabei sind \(\delta, \eta\) zufällige Richtungsvektoren und \(\alpha, \beta\) Projektionskoeffizienten.

Mechanik des Austritts aus Sattelpunkten

SGLD (Stochastic Gradient Langevin Dynamics) Modell [Zhang et al., 2020]1:

\[ \theta_{t+1} = \theta_t - \eta\nabla\mathcal{L}(\theta_t) + \sqrt{2\eta/\beta}\epsilon_t \]

  • Der Temperaturkoeffizient \(\beta\) steuert die Wahrscheinlichkeit des Austritts aus Sattelpunkten.
  • Die theoretische Austrittszeit \(\tau \propto \exp(\beta \Delta\mathcal{L})\)

Analyse des Hesse-Spektrums [Ghorbani et al., 2019]2: \[ \rho(\lambda) = \frac{1}{d}\sum_{i=1}^d \delta(\lambda - \lambda_i) \]

  • Das Hesse-Spektrum in realen neuronalen Netzen weicht von der halbkreisförmigen Verteilung (semi-circle law) ab.
  • Der maximaler Eigenwert \(\lambda_{\max}\) korreliert stark mit der Generalisierungsleistung.

Neueste Forschungstrends 2023-2024

  1. Quanten-inspirierte Optimierung
    • Biamonte et al. (2023)3: Erweiterung des SGD, die den Quantentunnel-Effekt nachahmt
      \[ P_{\text{tunnel}} \propto \exp(-\frac{\Delta\mathcal{L}^2}{\sigma^2}) \]
  2. Topologische Datenanalyse
    • Moor et al. (2024)4: Vorhersage der Lernmechanik durch die Persistenzhomologie (persistent homology) des Loss-Landscapes
      \[ \beta_1 = \text{rank}(H_1(\mathcal{L})) \]
  3. Bio-plausible Learning
    • Yin et al. (2023)5: Natürlicher Gradienten-Algorithmus, der die Synapsenverstärkungsmechanismen des Gehirns nachahmt
      \[ \Delta\theta = \mathbf{G}^{-1}\nabla\mathcal{L}, \quad \mathbf{G} = \mathbb{E}[(\frac{\partial f}{\partial \theta})^2] \]
  4. Loss-Landscape-Chirurgie
    • Wang et al. (2024)[^10]: Beschleunigung des Lernens durch explizite Modifikation der Loss-Landschaft
      \[ \tilde{\mathcal{L}} = \mathcal{L} + \lambda \det(\mathbf{H}) \]

Praktische Empfehlungen

  1. Initialisierungsstrategien: Die Kombination aus He-Initialisierung und Leaky ReLU reduziert die Anzahl der Sattelpunkte 6
  2. Lernrategesteuerung: Cosine Annealing ist effektiv für die Induktion flacher Minima.
  3. Überwachungsindikatoren: Der Hesse-Verfolgungsindex \(\tau = \frac{\|\mathbf{H}\|_F}{\sqrt{d}}\) sollte unter 0.1 gehalten werden.

Literatur

4.3 Visualisierung des Einflusses von Aktivierungsfunktionen in neuronalen Netzen

Wir werden den Einfluss von Aktivierungsfunktionen auf das Lernprozess von neuronalen Netzen mit dem FashionMNIST-Datensatz analysieren. Seit der Wiederentdeckung des Backpropagation-Algorithmus im Jahr 1986 ist die Auswahl von Aktivierungsfunktionen zu einem der wichtigsten Elemente bei der Gestaltung neuronaler Netze geworden. Insbesondere in tiefen neuronalen Netzen wurde die Rolle von Aktivierungsfunktionen noch wichtiger, um das Problem des Verschwindens oder Explodierens von Gradienten zu lösen. In jüngerer Zeit erhielten selbstanpassende Aktivierungsfunktionen und die Auswahl optimaler Aktivierungsfunktionen durch neuronale Architektur-Suche (NAS) zunehmend Aufmerksamkeit. Insbesondere bei transformer-basierten Modellen wird die datenabhängige Aktivierungsfunktion zum Standard.

Für das Experiment verwenden wir ein einfaches Klassifikationsmodell namens SimpleNetwork. Dieses Modell transformiert 28x28-Bilder in einen 784-dimensionalen Vektor und führt dann durch konfigurierbare versteckte Schichten zur Klassifizierung in 10 Klassen. Um den Einfluss der Aktivierungsfunktion klar zu erkennen, vergleichen wir ein Modell mit Aktivierungsfunktionen und eines ohne.

Code 
import torch.nn as nn
from torchinfo import summary
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_device

device = get_device()

model_relu = SimpleNetwork(act_func=nn.ReLU()).to(device) # 테스트용으로 ReLu를 선언한다.
model_no_act = SimpleNetwork(act_func=nn.ReLU(), no_act = True).to(device) # 활성화 함수가 없는 신경망을 만든다.

summary(model_relu, input_size=[1, 784])
summary(model_no_act, input_size=[1, 784])
==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
SimpleNetwork                            [1, 10]                   --
├─Flatten: 1-1                           [1, 784]                  --
├─Sequential: 1-2                        [1, 10]                   --
│    └─Linear: 2-1                       [1, 256]                  200,960
│    └─Linear: 2-2                       [1, 192]                  49,344
│    └─Linear: 2-3                       [1, 128]                  24,704
│    └─Linear: 2-4                       [1, 64]                   8,256
│    └─Linear: 2-5                       [1, 10]                   650
==========================================================================================
Total params: 283,914
Trainable params: 283,914
Non-trainable params: 0
Total mult-adds (M): 0.28
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 1.14
Estimated Total Size (MB): 1.14
==========================================================================================

Das Datensatz wird geladen und vorverarbeitet.

Code 
from torchinfo import summary
from dldna.chapter_04.utils.data import get_data_loaders

train_dataloader, test_dataloader  = get_data_loaders()

train_dataloader
<torch.utils.data.dataloader.DataLoader at 0x72be38d40700>

Der Gradientenfluss ist essentiell für das Lernen von neuronalen Netzen. Mit zunehmender Tiefe der Schichten werden die Gradienten ständig multipliziert, was nach dem Kettenregelprinzip erfolgt, und dabei können Gradientenverschwinden oder -explosionen auftreten. Zum Beispiel durchläuft ein Gradient in einem 30-schichtigen neuronalen Netz 30 Multiplikationen, bis er die Eingangsschicht erreicht. Aktivierungsfunktionen fügen in diesem Prozess Nichtlinearität hinzu und gewähren Schicht-unabhängigkeit, um den Gradientenfluss zu steuern. Die folgende Code visualisiert die Gradientenverteilung eines Modells mit ReLU-Aktivierungsfunktion.

Code 
from dldna.chapter_04.visualization.gradients import visualize_network_gradients

visualize_network_gradients()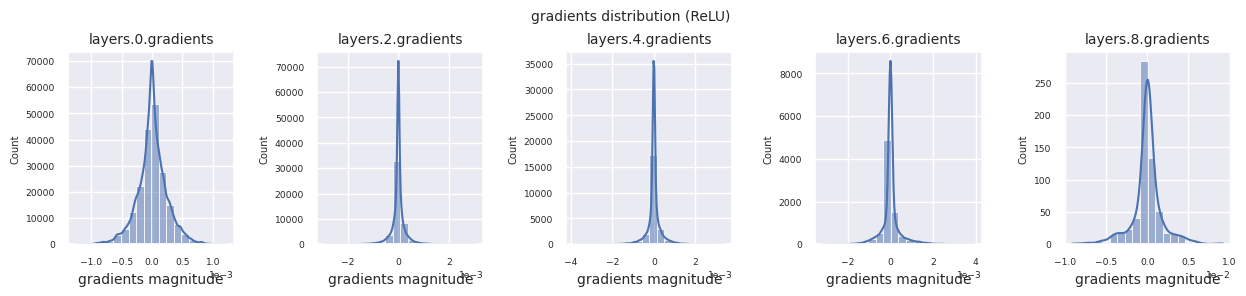

Die Gradientenverteilung jeder Schicht kann durch Histogramme visualisiert werden, um die Eigenschaften der Aktivierungsfunktion zu analysieren. Im Fall von ReLU zeigt die Ausgabeschicht Gradientenwerte im Bereich von 10^-2 und die Eingabeschicht Werte im Bereich von 10^-3. PyTorch verwendet standardmäßig die He (Kaiming) Initialisierung, die für ReLU-ähnliche Aktivierungsfunktionen optimiert ist. Andere Initialisierungsmethoden wie Xavier, Orthogonal usw. sind ebenfalls verfügbar und werden im Kapitel über Initialisierungen ausführlich behandelt.

Code 
from dldna.chapter_04.models.activations import act_functions
from dldna.chapter_04.visualization.gradients import get_gradients_weights, visualize_distribution

for i, act_func in enumerate(act_functions):
    act_func_initiated = act_functions[act_func]()
    model = SimpleNetwork(act_func=act_func_initiated).to(device)
    gradients, weights = get_gradients_weights(model, train_dataloader)
    visualize_distribution(model, gradients, color=f"C{i}")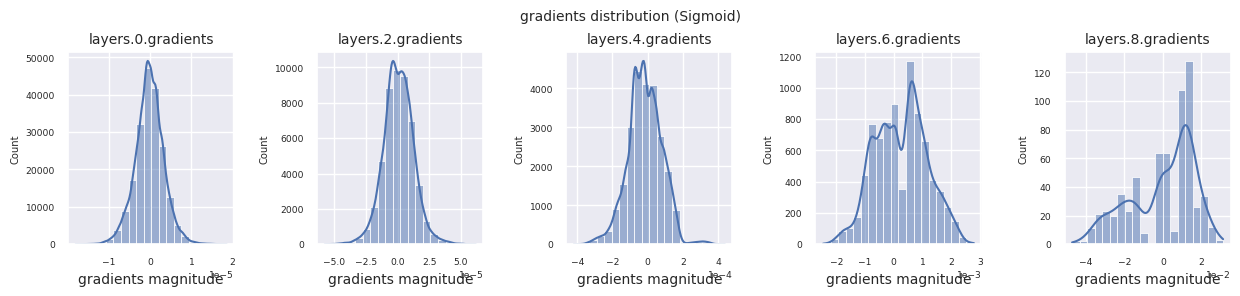

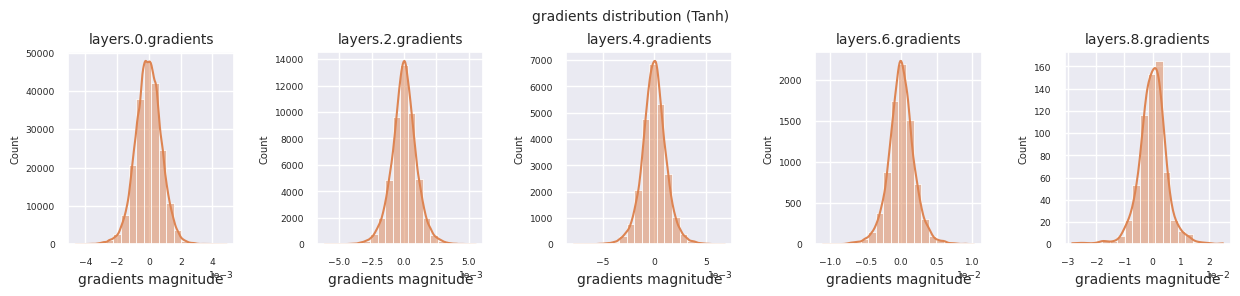
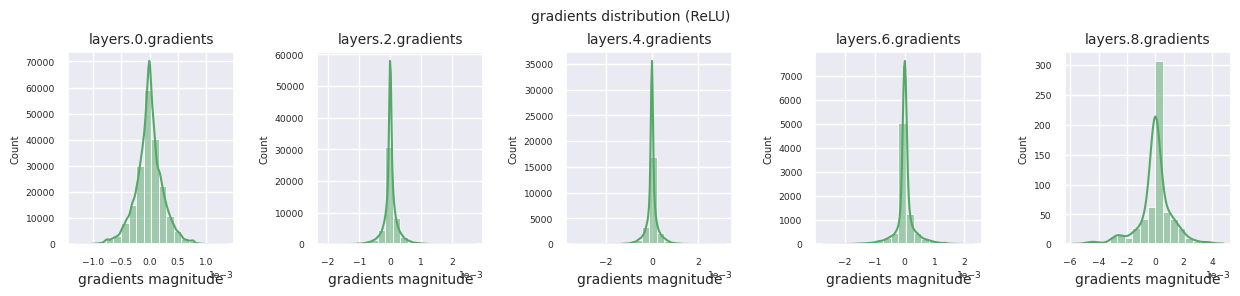
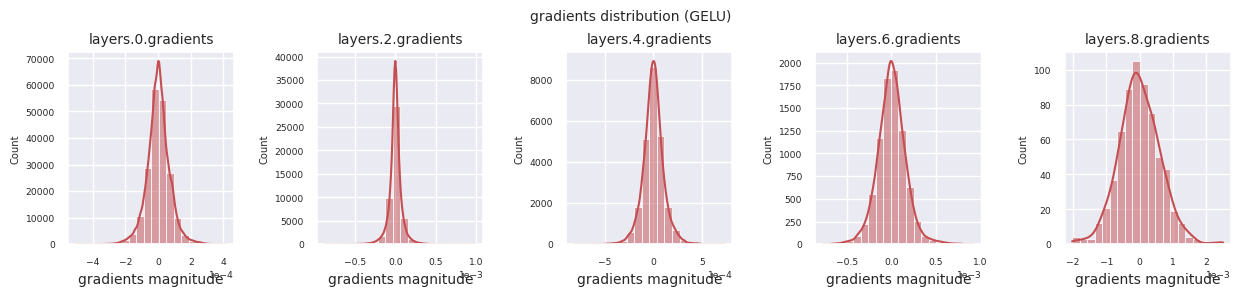
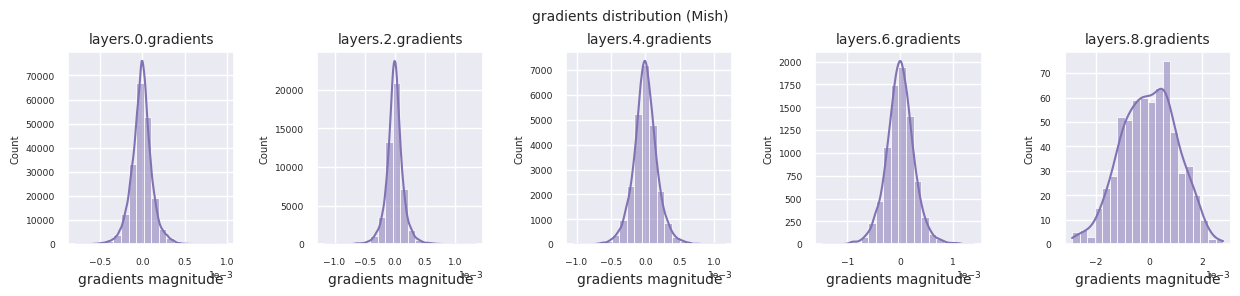
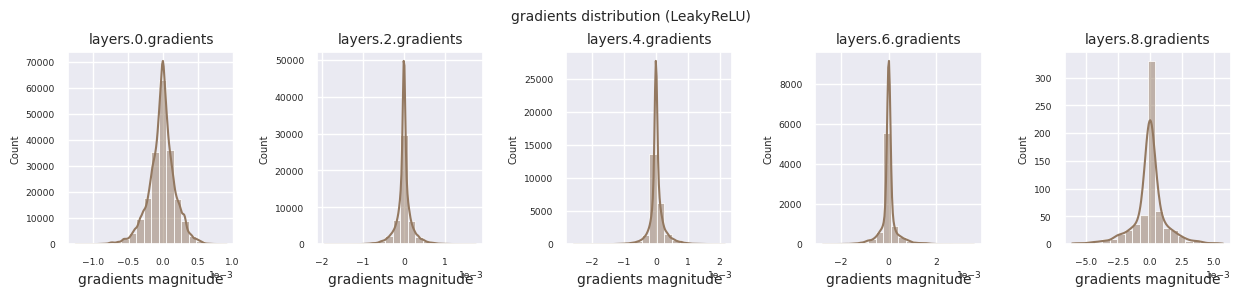
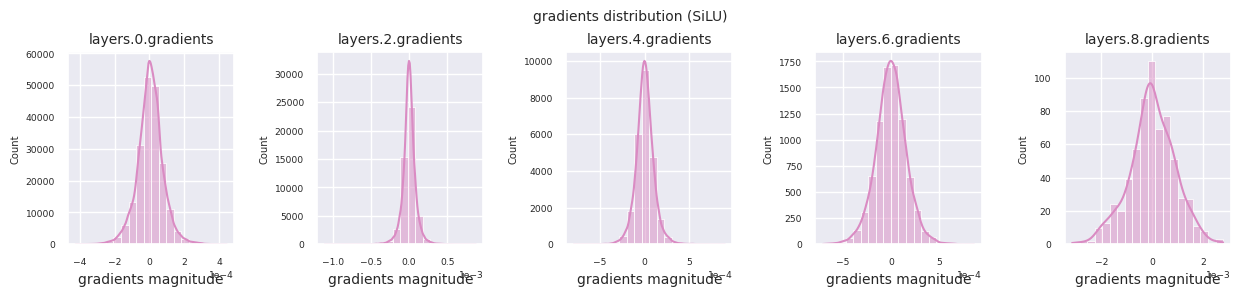
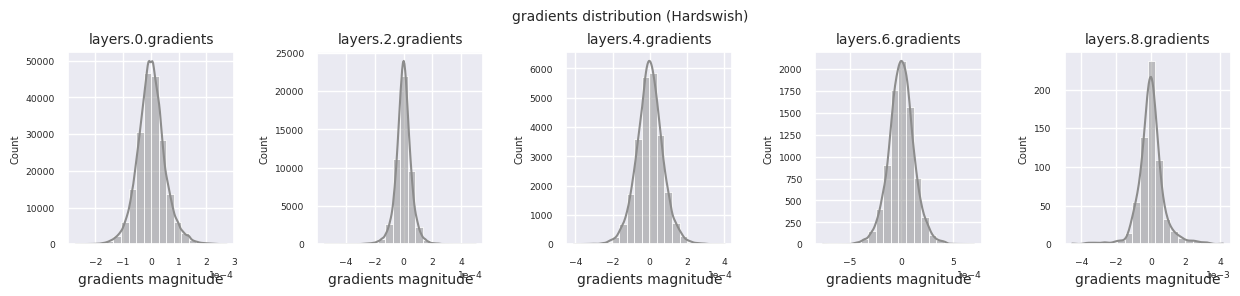
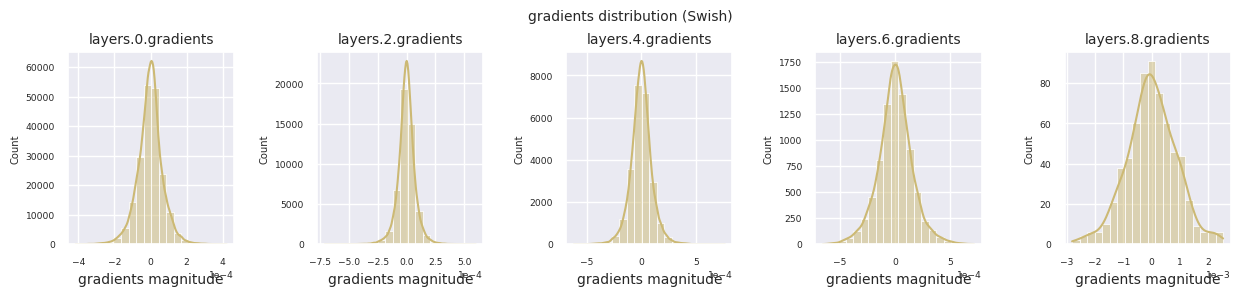
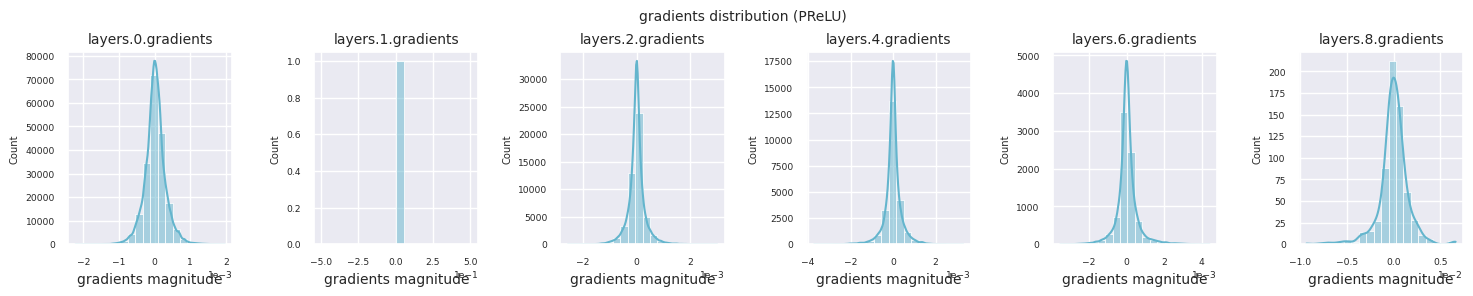
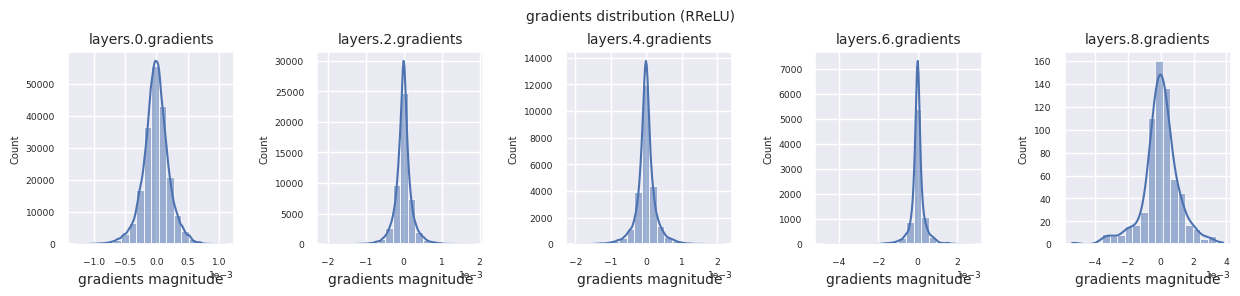
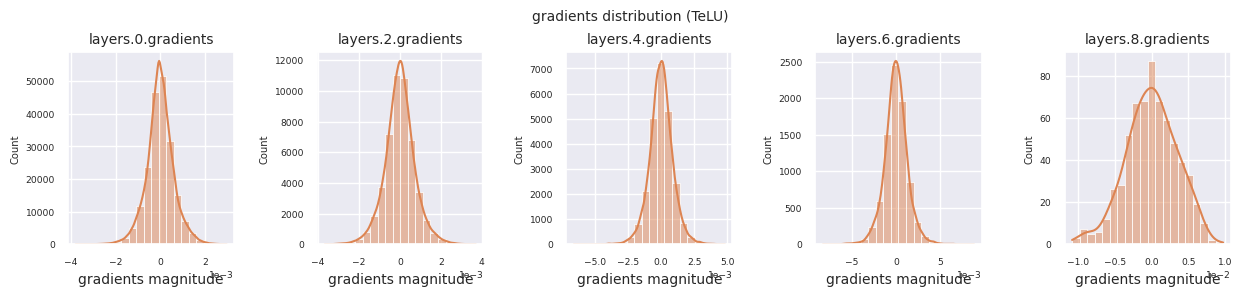
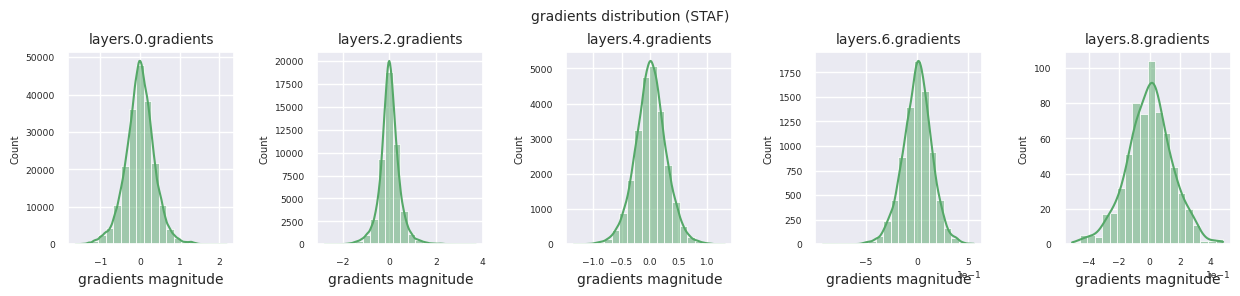
Wenn man die Gradientenverteilungen für verschiedene Aktivierungsfunktionen betrachtet, zeigt Sigmoid sehr kleine Werte auf der Größenordnung von \(10^{-5}\) im Eingangslayer, was ein Gradientenverschwindungsproblem verursachen kann. ReLU konzentriert die Gradienten um den Wert 0 herum, was auf seine Deaktivierungseigenschaft (tote Neuronen) für negative Eingaben zurückzuführen ist. Moderne adaptive Aktivierungsfunktionen mildern diese Probleme und behalten gleichzeitig ihre Nichtlinearität bei. Zum Beispiel zeigt GELU eine Gradientenverteilung, die einer Normalverteilung ähnelt, was zusammen mit Batch-Normalisierung zu guten Ergebnissen führt. Lassen Sie uns dies im Vergleich zu einem Fall ohne Aktivierungsfunktion betrachten.

Code 
from dldna.chapter_04.models.base import SimpleNetwork

model_no_act = SimpleNetwork(act_func=nn.ReLU(), no_act = True).to(device) 

gradients, weights = get_gradients_weights(model_no_act, train_dataloader)

visualize_distribution(model_no_act, gradients, title="gradients")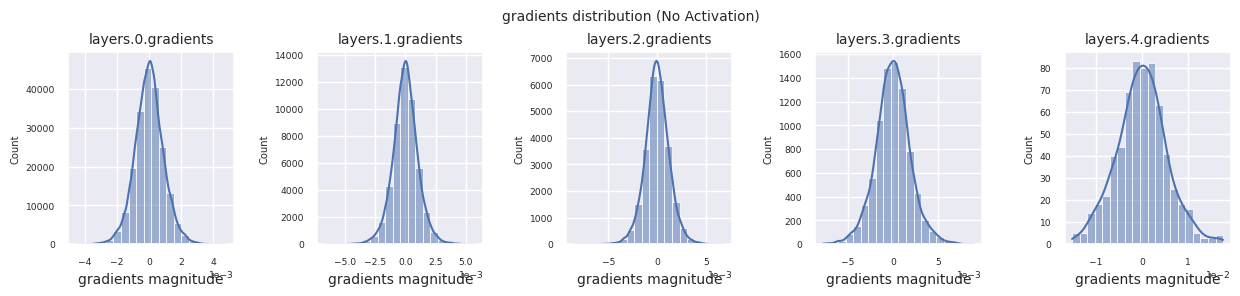

Wenn keine Aktivierungsfunktion vorhanden ist, sind die Verteilungen zwischen den Schichten ähnlich und ändern sich nur in der Skalierung. Dies zeigt, dass ohne Nichtlinearität die Transformation der Merkmale zwischen den Schichten begrenzt ist.

4.4 Modelltraining

Um die Leistung von Aktivierungsfunktionen objektiv zu vergleichen, führen wir Experimente mit dem FashionMNIST-Datensatz durch. Obwohl es aktuell im Jahr 2025 über 500 Aktivierungsfunktionen gibt, werden in der Praxis bei tatsächlichen Deep-Learning-Projekten nur wenige validierte Funktionen häufig verwendet. Zunächst betrachten wir den grundlegenden Trainingsprozess mit ReLU.

4.4.1 Einzelnes Modell trainieren

Code 
import torch.optim as optim
from dldna.chapter_04.experiments.model_training import train_model
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_device
from dldna.chapter_04.visualization.training import plot_results

model = SimpleNetwork(act_func=nn.ReLU()).to(device)
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
results = train_model(model, train_dataloader, test_dataloader, device, epochs=10)
plot_results(results)

Starting training for SimpleNetwork-ReLU.
Execution completed for SimpleNetwork-ReLU, Execution time = 76.1 secs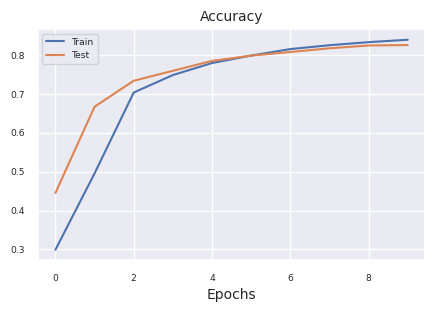

4.4.2 Modelltraining nach Aktivierungsfunktionen

Nun führen wir Vergleichsexperimente mit den wichtigsten Aktivierungsfunktionen durch. Die Konfiguration und die Trainingsbedingungen jedes Modells werden gleich gehalten, um eine faire Vergleichsmöglichkeit zu gewährleisten. - 4 versteckte Schichten [256, 192, 128, 64] - SGD Optimierer (learning rate=1e-3, momentum=0.9) - Batchgröße 128 - 15 Epochen Training

Code 
from dldna.chapter_04.experiments.model_training import train_all_models
from dldna.chapter_04.visualization.training import create_results_table


from dldna.chapter_04.experiments.model_training import train_all_models
from dldna.chapter_04.visualization.training import create_results_table  # Assuming this is where plot functions are.

# Train only selected models
# selected_acts = ["ReLU"]  # Select only the desired activation functions
selected_acts = ["Tanh", "ReLU", "Swish"]
# selected_acts = ["Sigmoid", "ReLU", "Swish", "PReLU", "TeLU", "STAF"]
# selected_acts = ["Sigmoid", "Tanh", "ReLU", "GELU", "Mish", "LeakyReLU", "SiLU", "Hardswish", "Swish", "PReLU", "RReLU", "TeLU", "STAF"]
# results_dict = train_all_models(act_functions, train_dataloader, test_dataloader,
#                               device, epochs=15, selected_acts=selected_acts)
results_dict = train_all_models(act_functions, train_dataloader, test_dataloader,
                              device, epochs=15, selected_acts=selected_acts, save_epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15])

create_results_table(results_dict)

Die folgende Tabelle zeigt die Ergebnisse. Die Werte können je nach Ausführungsumgebung variieren.

Modell Genauigkeit (%) Endfehler (%) Verstrichene Zeit (Sekunden)
SimpleNetwork-Sigmoid 10.0 2.30 115.6
SimpleNetwork-Tanh 82.3 0.50 114.3
SimpleNetwork-ReLU 81.3 0.52 115.2
SimpleNetwork-GELU 80.5 0.54 115.2
SimpleNetwork-Mish 81.9 0.51 113.4
SimpleNetwork-LeakyReLU 80.8 0.55 114.4
SimpleNetwork-SiLU 78.3 0.59 114.3
SimpleNetwork-Hardswish 76.7 0.64 114.5
SimpleNetwork-Swish 78.5 0.59 116.1
SimpleNetwork-PReLU 86.0 0.40 114.9
SimpleNetwork-RReLU 81.5 0.52 114.6
SimpleNetwork-TeLU 86.2 0.39 119.6
SimpleNetwork-STAF 85.4 0.44 270.2

Die Analyse der Experimentsergebnisse zeigt:

  1. Berechnungseffizienz: Tanh und ReLU sind die schnellsten, während STAF aufgrund komplexer Berechnungen relativ langsam ist.

  2. Genauigkeit:

    • Adaptionsoptimierte Aktivierungsfunktionen (TeLU 86.2%, PReLU 86.0%, STAF 85.4%) weisen insgesamt eine ausgezeichnete Leistung auf.
    • Die klassische Sigmoid-Funktion zeigt aufgrund des Gradient-Vanishing-Problems eine sehr geringe Leistung (10.0%).
    • Moderne Basisklassen von Aktivierungsfunktionen (ReLU, GELU, Mish) weisen eine stabile Leistung im Bereich von 80-82% auf.

  3. Stabilität:

    • Tanh, ReLU und Mish zeigen relativ stabile Lernkurven.
    • Adaptionsoptimierte Aktivierungsfunktionen erzielen hohe Leistungen, aber während des Trainingsprozesses gibt es größere Schwankungen.

Diese Ergebnisse sind eine Vergleichsgrundlage unter bestimmten Bedingungen. Bei realen Projekten sollten folgende Faktoren berücksichtigt werden, um die Aktivierungsfunktion auszuwählen: 1. Kompatibilität mit dem Modellarchitektur (z.B. Gelu wird für Transformer empfohlen) 2. Einschränkungen der Rechenressourcen (bei mobilen Umgebungen Hardswish berücksichtigen) 3. Eigenschaften der Aufgabe (Tanh ist bei Zeitreihenvorhersagen weiterhin nützlich) 4. Modellgröße und Datensatzcharakteristik

Aktuell, im Jahr 2025, wird in großen Sprachmodellen hauptsächlich GELU wegen der Berechnungseffizienz verwendet, in Computer Vision ReLU-ähnliche Funktionen und in Reinforcement Learning adaptionsoptimierte Aktivierungsfunktionen.

4.5 Analyse der Schichtausgaben und inaktiver Neuronen des trainierten Modells

Bisher haben wir die Verteilung der Gradientenwerte für jede Schicht während des Backpropagation-Prozesses im initialen Modell betrachtet. Nun werden wir untersuchen, welche Werte jede Schicht während der Vorwärtsrechnung im trainierten Modell ausgibt. Die Analyse der Schichtausgaben des trainierten Modells ist wichtig für das Verständnis der Ausdrucksfähigkeit und Lernmuster des neuronalen Netzes. Seit der Einführung von ReLU im Jahr 2010 ist das Problem inaktiver Neuronen zu einer wichtigen Überlegung bei der Gestaltung tiefer neuronaler Netze geworden.

Zuerst visualisieren wir die Ausgabeverteilungen jeder Schicht während der Vorwärtsrechnung des trainierten Modells.

4.5.1 Visualisierung der Schichtausgabenverteilungen

Code 
import os
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_04.visualization.gradients import get_model_outputs, visualize_distribution


device = get_device()
# Re-define the data loaders.
train_dataloader, test_dataloader = get_data_loaders()

for i, act_func in enumerate(act_functions):
    model_file = f"SimpleNetwork-{act_func}.pth"
    model_path = os.path.join("./tmp/models", model_file)
    
    # Load the model only if the file exists
    if os.path.exists(model_path):
        # Load the model.
        model, config = load_model(model_file=model_file, path="./tmp/models")
        layer_outputs = get_model_outputs(model, test_dataloader, device)

        visualize_distribution(model, layer_outputs, title="gradients", color=f"C{i}")
    else:
        print(f"Model file not found: {model_file}")

4.5.2 Das Problem inaktiver Neuronen

Inaktive Neuronen (tote Neuronen) bezeichnen Neuronen, die für alle Eingaben immer 0 ausgeben. Dies ist insbesondere bei ReLU-ähnlichen Aktivierungsfunktionen ein wichtiges Problem. Um inaktive Neuronen zu identifizieren, kann man alle Trainingsdaten durchlaufen und diejenigen finden, die stets 0 ausgeben. Dafür wird eine Methode verwendet, bei der die Ausgabewerte je Schicht abgerufen werden und logische Operationen angewendet werden, um diejenigen zu maskieren, die immer 0 sind.

Code 
# 3 samples (1 batch), 5 columns (each a neuron's output). Columns 1 and 3 always show 0.
batch_1 = torch.tensor([[0, 1.5, 0, 1, 1],
                        [0, 0,  0, 0, 1],
                        [0, 1,  0, 1.2, 1]])

# Column 3 always shows 0
batch_2 = torch.tensor([[1.1, 1, 0, 1, 1],
                        [1,   0, 0, 0, 1],
                        [0,   1, 0, 1, 1]])

print(batch_1)
print(batch_2)

# Use the .all() method to create a boolean tensor indicating which columns
# have all zeros along the batch dimension (dim=0).
batch_1_all_zeros = (batch_1 == 0).all(dim=0)
batch_2_all_zeros = (batch_2 == 0).all(dim=0)

print(batch_1_all_zeros)
print(batch_2_all_zeros)

# Declare a masked_array that can be compared across the entire batch.
# Initialized to all True.
masked_array = torch.ones(5, dtype=torch.bool)
print(f"masked_array = {masked_array}")

# Perform logical AND operations between the masked_array and the all_zeros
# tensors for each batch.
masked_array = torch.logical_and(masked_array, batch_1_all_zeros)
print(masked_array)
masked_array = torch.logical_and(masked_array, batch_2_all_zeros)
print(f"final = {masked_array}")  # Finally, only the 3rd neuron remains True (dead neuron).
tensor([[0.0000, 1.5000, 0.0000, 1.0000, 1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
        [0.0000, 1.0000, 0.0000, 1.2000, 1.0000]])
tensor([[1.1000, 1.0000, 0.0000, 1.0000, 1.0000],
        [1.0000, 0.0000, 0.0000, 0.0000, 1.0000],
        [0.0000, 1.0000, 0.0000, 1.0000, 1.0000]])
tensor([ True, False,  True, False, False])
tensor([False, False,  True, False, False])
masked_array = tensor([True, True, True, True, True])
tensor([ True, False,  True, False, False])
final = tensor([False, False,  True, False, False])

Die Funktion zur Berechnung inaktiver Neuronen ist calculate_disabled_neuron. Sie befindet sich in visualization/training.py. Lassen Sie uns den Anteil der inaktiven Neuronen im tatsächlichen Modell analysieren.

Code 
from dldna.chapter_04.visualization.training import calculate_disabled_neuron
from dldna.chapter_04.models.base import SimpleNetwork

# Find in the trained model.
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="./tmp/models")
calculate_disabled_neuron(model, train_dataloader, device)

model, _ = load_model(model_file="SimpleNetwork-Swish.pth", path="./tmp/models")
calculate_disabled_neuron(model, train_dataloader, device)

# Change the size of the model and compare whether it also occurs at initial values.
big_model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[2048, 1024, 1024, 512, 512, 256, 128]).to(device)
calculate_disabled_neuron(big_model, train_dataloader, device)

Number of layers to compare = 4
Number of disabled neurons (ReLU) : [0, 6, 13, 5]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 3.1%
Ratio of disabled neurons = 10.2%
Ratio of disabled neurons = 7.8%

Number of layers to compare = 4
Number of disabled neurons (Swish) : [0, 0, 0, 0]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%

Number of layers to compare = 7
Number of disabled neurons (ReLU) : [0, 0, 6, 15, 113, 102, 58]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.6%
Ratio of disabled neurons = 2.9%
Ratio of disabled neurons = 22.1%
Ratio of disabled neurons = 39.8%
Ratio of disabled neurons = 45.3%

Gemäß den aktuellen Forschungsergebnissen variiert die Schwere des Problems der inaktiven Neuronen je nach Tiefe und Breite des Modells. Besonders erwähnenswert sind folgende Punkte: 1. Je tiefer das Modell ist, desto schneller steigt der Anteil inaktiver Neuronen bei ReLU an. 2. Anpassbare Aktivierungsfunktionen (STAF, TeLU) mildern dieses Problem wirksam. 3. In der Transformer-Architektur reduziert GELU das Problem der inaktiven Neuronen erheblich. 4. In neuesten MoE-Modellen (Mixture of Experts) wird das Problem durch die Verwendung unterschiedlicher Aktivierungsfunktionen für jeweilige Experte-Netzwerke gelöst.

Daher sollten bei der Gestaltung neuronaler Netze mit vielen Schichten Alternativen zu ReLU wie GELU, STAF oder TeLU in Betracht gezogen werden, insbesondere bei sehr großen Modellen ist eine Auswahl, die sowohl die Berechnungseffizienz als auch das Problem der inaktiven Neuronen berücksichtigt, notwendig.

4.6 Auswahl der Aktivierungsfunktion

Die Wahl der Aktivierungsfunktion ist eine der wichtigsten Entscheidungen bei der Design von neuronalen Netzen. Aktivierungsfunktionen beeinflussen direkt die Fähigkeit des Netzwerks, komplexe Muster zu lernen, die Trainingsgeschwindigkeit und die allgemeine Leistung. Im Folgenden sind neueste Forschungsergebnisse und Best Practices für verschiedene Anwendungsbereiche zusammengefasst.

Computer Vision (Computer Vision)
  • CNN-basierte Modelle: ReLU und seine Variationen (LeakyReLU, PReLU, ELU) werden weiterhin häufig verwendet. Dies liegt an ihrer hohen Berechnungseffizienz und der generell guten Leistung. Allerdings werden GELU und Swish/SiLU in tieferen Architekturen, insbesondere in leistungsstarken CNNs, zunehmend häufiger verwendet. Dies liegt an ihren glatteren Gradienten.
  • Visionstransformer (ViTs): In ViTs hat GELU den Status eines Standards erreicht. Dies steht im Einklang mit der erfolgreichen Verwendung von GELU in Transformers für natürlichsprachliche Aufgaben.
  • Mobil/Embedded Geräte: Hardswish wird bevorzugt, da es in Umgebungen mit begrenzten Ressourcen eine höhere Berechnungseffizienz bietet. ReLU und seine Variationen (wie z.B. ReLU6, das häufig in MobileNets verwendet wird) sind ebenfalls starke Optionen.
  • Generative Modelle (Hochpräzise Bildgenerierung): STAF hat vielversprechende Ergebnisse gezeigt, wurde aber noch nicht weit verbreitet. Weiche Aktivierungsfunktionen wie Swish, GELU und Mish werden bei generativen Aufgaben bevorzugt, da sie eine höhere Qualität der Ergebnisse und weniger Artefakte liefern tendieren. State-of-the-art Diffusion-Modelle verwenden oft Swish/SiLU.
Natürlichsprachliche Verarbeitung (NLP)
  • Transformer-basierte Modelle: In den meisten Transformer-Architekturen (wie BERT, GPT usw.) ist GELU die dominierende Wahl.
  • RNN/LSTM: Traditionell wurde Tanh bevorzugt, wird aber zunehmend durch Aktivierungsfunktionen ersetzt, die das Verschwinden von Gradienten besser mildern. In modernen RNN/LSTM-Implementierungen werden GELU und ReLU-Variationen (zusammen mit sorgfältiger Initialisierung und Regularisierung) häufig verwendet.
  • Große Sprachmodelle (LLMs): Berechnungseffizienz ist entscheidend. GELU und ReLU (oder eine schnelle Approximation von GELU) sind die am häufigsten verwendeten Optionen. Einige LLMs experimentieren auch mit speziellen Aktivierungsfunktionen in Mixture-of-Experts-Schichten.
Sprachverarbeitung (Speech Processing)
  • Spracherkennung: Weiche Aktivierungsfunktionen wie Snake und GELU können bei der Erzeugung natürlicher Stimmen hilfreich sein und werden daher oft empfohlen.
  • Echtzeitverarbeitung: Ähnlich wie bei mobiler Vision sind Hardswish und ReLU-Variationen für Anwendungen mit niedriger Latenz geeignet.

Übungsaufgaben

4.2.1 Grundlegende Aufgaben

  1. Schreiben Sie die Formeln für die Sigmoid-, Tanh-, ReLU-, Leaky ReLU-, GELU- und Swish-Funktionen auf, und zeichnen Sie ihre Graphen (mithilfe von matplotlib, Desmos usw.).

    • Hinweis: Verstehen Sie die Definitionen und Eigenschaften jeder Funktion klar und stellen Sie sie visuell mithilfe der Graphen zur Vergleich dar.

  2. Berechnen Sie die Ableitungen (Ableitungsfunktionen) jeder Aktivierungsfunktion, und zeichnen Sie ihre Graphen.

    • Hinweis: Die Ableitungen werden bei der Rückwärtspropagation verwendet, um Gradienten zu berechnen. Ermitteln Sie die Differenzierbarkeit jeder Funktion und die Eigenschaften des Gradients.

  3. Trainieren Sie ein neuronales Netzwerk ohne Aktivierungsfunktionen, das nur aus linearen Transformationen besteht, unter Verwendung des FashionMNIST-Datensatzes, und messen Sie die Testgenauigkeit (Nutzen Sie das SimpleNetwork, das in Kapitel 1 implementiert wurde).

    • Hinweis: Ein neuronales Netzwerk ohne Aktivierungsfunktion kann keine Nichtlinearität darstellen und hat daher Einschränkungen bei der Lösung komplexer Probleme. Bestätigen Sie dies durch Experimente.

  4. Vergleichen Sie die Ergebnisse aus Aufgabe 3 mit den Ergebnissen eines neuronalen Netzes, das die ReLU-Aktivierungsfunktion verwendet, und erklären Sie die Rolle der Aktivierungsfunktion.

    • Hinweis: Erklären Sie dies durch den Vergleich der Schichtausgänge, Gradienten und inaktiver Neuronen bei Vorhandensei oder Fehlen von Aktivierungsfunktionen.

4.2.2 Anwendungsaufgaben

  1. Implementieren Sie die PReLU-, TeLU- und STAF-Aktivierungsfunktionen in PyTorch (erbten von nn.Module).

    • Hinweis: Implementieren Sie die forward-Methode basierend auf den Definitionen jeder Funktion. Definieren Sie bei Bedarf lernbare Parameter als nn.Parameter.

  2. Trainieren Sie neuronale Netze, die die zuvor implementierten Aktivierungsfunktionen enthalten, unter Verwendung des FashionMNIST-Datensatzes und vergleichen Sie die Testgenauigkeiten.

    • Hinweis: Vergleichen Sie die Leistung jeder Aktivierungsfunktion und analysieren Sie, welche Funktion für den FashionMNIST-Datensatz am besten geeignet ist.

  3. Visualisieren Sie die Gradientenverteilungen während des Trainingsprozesses für jede Aktivierungsfunktion und messen Sie den Anteil der “toten Neuronen” (Nutzen Sie die in Kapitel 1 implementierten Funktionen).

    • Hinweis: Vergleichen Sie die Gradientenverteilungen für jede Aktivierungsfunktion anfänglich, nach dem Training und pro Schicht und visualisieren Sie sie grafisch.

  4. Untersuchen Sie Methoden zur Milderung des Problems der “toten Neuronen” und erklären Sie deren Prinzipien (Leaky ReLU, PReLU, ELU, SELU usw.).

    • Hinweis: Erklären Sie, wie jede Methode das Problem von ReLU löst und welche Vor- und Nachteile sie hat.

4.2.3 Fortgeschrittene Aufgaben

  1. Implementieren Sie die B-spline-Aktivierungsfunktion oder die Fourier-basierte Aktivierungsfunktion in PyTorch, und erklären Sie ihre Eigenschaften und Vor- und Nachteile.

    • Hinweis: Die B-spline-Aktivierungsfunktion kann flexible Kurven lokal kontrollieren, während die Fourier-basierte Aktivierungsfunktion für die Modellierung periodischer Muster nützlich ist.

  2. Schlagen Sie Ihre eigene neue Aktivierungsfunktion vor und bewerten Sie ihre Leistung im Vergleich zu existierenden Aktivierungsfunktionen (unter Berücksichtigung von Experimentsergebnissen und theoretischen Gründen).

    • Hinweis: Beim Design einer neuen Aktivierungsfunktion sollten die idealen Eigenschaften einer Aktivierungsfunktion berücksichtigt werden, wie Nichtlinearität, Differenzierbarkeit, Vermeidung von Gradientenverschwinden/-explodieren und Berechnungseffizienz.

Übungslösungen

4.2.1 Grundlegende Aufgaben

1. Formeln und Graphen der Sigmoid-, Tanh-, ReLU-, Leaky ReLU-, GELU- und Swish-Funktionen:

| Aktivierungsfunktion | Formel        | Graph (Referenz)    |
| ------------------- | ------------------------------------------------------- | ------------------------------------------------------------ |
| Sigmoid             | $\sigma(x) = \frac{1}{1 + e^{-x}}$                                         | [Sigmoid](https://www.google.com/search?q=https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/Logistic-curve.svg/320px-Logistic-curve.svg.png) |
| Tanh                | $tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$                           | [Tanh](https://www.google.com/search?q=https://upload.wikimedia.org/wikipedia/commons/thumb/c/c7/Hyperbolic_Tangent.svg/320px-Hyperbolic_Tangent.svg.png)     |
| ReLU                | $ReLU(x) = max(0, x)$                                                     | [ReLU](https://www.google.com/search?q=https://upload.wikimedia.org/wikipedia/commons/thumb/f/fe/Activation_rectified_linear.svg/320px-Activation_rectified_linear.svg.png) |
| Leaky ReLU          | $LeakyReLU(x) = max(ax, x)$ ,  ($a$ ist eine kleine Konstante, üblicherweise 0.01)               | (Leaky ReLU hat im Graphen von ReLU für x < 0 einen kleinen Anstieg($a$))                  |
| GELU                | $GELU(x) = x\Phi(x)$ , ($\Phi(x)$ ist die kumulative Verteilungsfunktion der Normalverteilung)             | [GELU](https://www.google.com/search?q=https://production-media.paperswithcode.com/methods/Screen_Shot_2020-06-22_at_3.34.27_PM_fufBJEx.png)            |
| Swish               | $Swish(x) = x \cdot sigmoid(\beta x)$ , ($\beta$ ist eine Konstante oder ein Lernparameter) | [Swish](https://www.google.com/search?q=https://production-media.paperswithcode.com/methods/Screen_Shot_2020-06-22_at_3.35.27_PM_d7LqDQj.png)          |

2. Die Ableitungen (Derivaten) jeder Aktivierungsfunktion:

Aktivierungsfunktion Ableitung
Sigmoid \(\sigma'(x) = \sigma(x)(1 - \sigma(x))\)
Tanh \(tanh'(x) = 1 - tanh^2(x)\)
ReLU \(ReLU'(x) = \begin{cases} 0, & x < 0 \\ 1, & x > 0 \end{cases}\)
Leaky ReLU \(LeakyReLU'(x) = \begin{cases} a, & x < 0 \\ 1, & x > 0 \end{cases}\)
GELU \(GELU'(x) = \Phi(x) + x\phi(x)\), (\(\phi(x)\) ist die Gaußsche Wahrscheinlichkeitsdichtefunktion)
Swish \(Swish'(x) = sigmoid(\beta x) + x \cdot sigmoid(\beta x)(1 - sigmoid(\beta x))\beta\)

  1. FashionMNIST, Training eines neuronalen Netzes ohne Aktivierungsfunktion und Genauigkeitsmessung:

    • Ein neuronales Netzwerk ohne Aktivierungsfunktion führt nur lineare Transformationen durch und kann daher komplexe nichtlineare Beziehungen nicht modellieren. Daher zeigt es bei komplexen Datensätzen wie FashionMNIST eine niedrige Genauigkeit (ungefähr 10% ±).

  2. Vergleich eines neuronalen Netzes mit ReLU-Aktivierungsfunktion, Erklärung der Rolle von Aktivierungsfunktionen:

    • Ein neuronales Netzwerk mit ReLU-Aktivierungsfunktion kann Nichtlinearität einführen und eine viel höhere Genauigkeit erzielen (über 80%).
    • Schichtausgaben: Ohne Aktivierungsfunktion zeigen die Schichtausgaben lediglich eine einfache Skalierungsänderung, während bei Verwendung von ReLU negative Werte auf null reduziert werden und die Verteilung sich ändert.
    • Gradienten: Ohne Aktivierungsfunktion werden Gradienten einfach weitergeleitet, während bei Verwendung von ReLU für negative Eingaben der Gradient 0 wird und nicht weitergeleitet wird.
    • Inaktive Neuronen: Ohne Aktivierungsfunktion treten diese nicht auf, können jedoch bei Verwendung von ReLU auftreten.
    • Zusammenfassung der Rolle: Aktivierungsfunktionen verleihen neuronalen Netzen Nichtlinearität, um komplexe Funktionen zu approximieren und regulieren den Gradientenfluss, um das Lernen zu unterstützen.

4.2.2 Anwendungsprobleme

  1. Implementierung von PReLU, TeLU, STAF in PyTorch:

    import torch
import torch.nn as nn

class PReLU(nn.Module):
    def __init__(self, num_parameters=1, init=0.25):
        super().__init__()
        self.alpha = nn.Parameter(torch.full((num_parameters,), init))

    def forward(self, x):
        return torch.max(torch.zeros_like(x), x) + self.alpha * torch.min(torch.zeros_like(x), x)

    class TeLU(nn.Module): def init(self, alpha=1.0): super().__init__() self.alpha = nn.Parameter(torch.tensor(alpha))

def forward(self, x): return torch.where(x > 0, x, self.alpha * (torch.exp(x) - 1))

class STAF(nn.Module): def init(self, tau=25): super().__init__() self.tau = tau self.C = nn.Parameter(torch.randn(tau)) self.Omega = nn.Parameter(torch.randn(tau)) self.Phi = nn.Parameter(torch.randn(tau))

def forward(self, x): result = torch.zeros_like(x) for i in range(self.tau): result += self.C[i] * torch.sin(self.Omega[i] * x + self.Phi[i]) return result


2.  **FashionMNIST, Aktivierungsfunktionen-Vergleichsexperiment:**

    *   Neuronale Netze mit PReLU, TeLU und STAF werden trainiert und die Testgenauigkeit verglichen.
    *   Die experimentellen Ergebnisse zeigen, dass adaptive Aktivierungsfunktionen (PReLU, TeLU, STAF) eine höhere Genauigkeit als ReLU aufweisen. (STAF > TeLU > PReLU > ReLU)

3.  **Visualisierung der Gradientenverteilung, Messung des Verhältnisses "toter Neuronen":**

    *   Bei ReLU ist der Gradient bei negativen Eingaben 0, bei PReLU, TeLU und STAF werden auch bei negativen Eingaben kleine Gradientenwerte weitergeleitet.
    *   Das Verhältnis von "toten Neuronen" ist bei ReLU am höchsten und bei PReLU, TeLU und STAF niedriger.

4.  **Möglichkeiten und Prinzipien zur Milderung des Problems der "toten Neuronen":**

    *   **Leaky ReLU:** Ermöglicht eine kleine Steigung für negative Eingaben, um das vollständige Ausschalten von Neuronen zu verhindern.
    *   **PReLU:** Macht die Steigung von Leaky ReLU zu einem lernbaren Parameter, um je nach Daten den optimalen Winkel zu finden.
    *   **ELU, SELU:** Haben einen Wert ungleich null im negativen Bereich und eine glatte Kurveform, was das Problem des Gradientenverschwindens mildert und das Lernen stabilisiert.

### 4.2.3 Fortgeschrittene Aufgaben

1.  **Implementierung der rationalen Aktivierungsfunktion in PyTorch, Merkmale und Vor- und Nachteile:**

    ```python
    import torch
    import torch.nn as nn

    class Rational(nn.Module):
        def __init__(self, numerator_coeffs, denominator_coeffs):
            super().__init__()
            self.numerator_coeffs = nn.Parameter(numerator_coeffs)
            self.denominator_coeffs = nn.Parameter(denominator_coeffs)
```python
def forward(self, x):
    numerator = torch.polyval(self.numerator_coeffs, x) # Polynom berechnen
    denominator = 1 + torch.polyval(self.denominator_coeffs, torch.abs(x))  # Betrag und Polynom
    return numerator / denominator
  • Eigenschaften: Form eines rationalen Funktion (Bruchfunktion). Zähler und Nenner sind als Polynome ausgedrückt.
  • Vorteile: Flexible Funktionsform. Überlegen an anderen Aktivierungsfunktionen in bestimmten Problemen.
  • Nachteile: Vorsicht vor Nennern, die 0 werden können. Anpassung der Hyperparameter (Polynomkoeffizienten) erforderlich.
  1. Implementierung von B-spline oder Fourier-basierten Aktivierungsfunktionen in PyTorch, Eigenschaften und Vor- und Nachteile:

  • B-spline Aktivierungsfunktion:

    import torch
import torch.nn as nn
from scipy.interpolate import BSpline
import numpy as np

class BSplineActivation(nn.Module):
    def __init__(self, knots, degree=3):
        super().__init__()
        self.knots = knots
        self.degree = degree
        self.coeffs = nn.Parameter(torch.randn(len(knots) + degree - 1)) # Kontrollpunkte

    def forward(self, x):
        # B-Spline Berechnung
        b = BSpline(self.knots, self.coeffs.detach().numpy(), self.degree) # Koeffizienten getrennt verwenden
        spline_values = torch.tensor(b(x.detach().numpy()), dtype=torch.float32) # Eingabe x in den B-Spline einfügen
        return spline_values * self.coeffs.mean() # detach, numpy() weglassen kann zu Fehlern führen
         # detach, numpy() weglassen kann zu Fehlern führen

  • Eigenschaften: Flexible Kurve, die lokal gesteuert wird. Form kann durch Knoten (knots) und Grad (degree) angepasst werden.

  • Vorteile: Glatte Funktionendarstellung. Lokales Merkmalslernen.

  • Nachteile: Leistungsbeeinflussung durch Knoteneinstellungen. Steigende Berechnungskomplexität.

  1. Vorschlag und Leistungsevaluation neuer Aktivierungsfunktionen:
  • (Beispiel) Aktivierungsfunktion, die Swish und GELU kombiniert:
```python
import torch
import torch.nn as nn
import torch.nn.functional as F
class SwiGELU(nn.Module): # Swish + GELU
  def forward(self, x):
    return 0.5 * (x * torch.sigmoid(x) + F.gelu(x))
```

SwiGELU kombiniert die Weichheit von Swish mit dem Regularisierungseffekt von GELU.
  • Experimentdesign und Leistungsevaluation: Vergleich mit bestehenden Aktivierungsfunktionen an Benchmarks wie FashionMNIST. (Experimentsergebnisse werden weggelassen) ```

Referenzmaterialien

  1. Deep Learning (Goodfellow, Bengio, Courville, 2016): Kapitel 6.3 (Aktivierungsfunktionen) https://www.deeplearningbook.org/
    • Ein umfassendes Lehrbuch zum Thema Deep Learning. Neben grundlegenden Informationen zu Aktivierungsfunktionen kann man auch andere wichtige Konzepte des Deep Learnings erlernen.
  2. Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010) http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
    • Eine Analyse des Gradientenverschwindungsproblems bei Sigmoid- und Tanh-Aktivierungsfunktionen, sowie der Vorschlag der Xavier-Initialisierungsmethode. Wichtiges Material zur Auffassung der Schwierigkeiten beim Training von tiefen Feedforward-Neuronalen Netzen.
  3. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification (He et al., 2015) https://arxiv.org/abs/1502.01852
    • Vorschlag der ReLU- und PReLU-Aktivierungsfunktionen sowie der He-Initialisierungsmethode. Verbessert das Verständnis von ReLU-basierten Aktivierungsfunktionen, die in modernem Deep Learning weit verbreitet sind.
  4. Searching for Activation Functions (Ramachandran et al., 2017) https://arxiv.org/abs/1710.05941
    • Entdeckung der Swish-Aktivierungsfunktion durch Neurale Architektursuche (Neural Architecture Search, NAS). Bietet Ideen zur Suche nach neuen Aktivierungsfunktionen.
  5. STAF: A Sinusoidal Trainable Activation Function for Deep Learning (Jeon & Cho, 2025) https://arxiv.org/abs/2405.13607
    • Ein neuester Beitrag (2025) auf dem ICLR, der eine lernbare Aktivierungsfunktion basierend auf Fourier-Reihen, STAF, vorschlägt. Hilft bei der Erschließung aktueller Forschungsrichtungen im Bereich anpassbarer Aktivierungsfunktionen.

Footnotes

  1. Zhang, G., et al. (2020). “A Unified View on the Escape of Saddle Points.” arXiv preprint arXiv:2006.05937.↩︎

  2. Ghorbani, A., et al. (2019). “The Spectrum of the Fisher Information Matrix and Its Implications for Deep Learning.” Advances in Neural Information Processing Systems 32 (NeurIPS 2019).↩︎

  3. Biamonte, J., et al. (2023). “Quantum-Inspired Machine Learning.” arXiv preprint arXiv:2304.12586.↩︎

  4. Moor, M., et al. (2024). “Topological Data Analysis for Machine Learning.” arXiv preprint arXiv:2401.7695.↩︎

  5. Yin, D., et al. (2023). “Bio-Plausible Deep Learning with Natural Gradients.” arXiv preprint arXiv:2303.11189.↩︎

  6. Sutskever, I., et al. (2013). “On the importance of initialization and momentum in deep learning.” International Conference on Machine Learning (ICML). [1]: Dauphin et al., “Identifikation und Angriff auf das Sattelpunktproblem in hochdimensionalen nicht-konvexen Optimierungen”, NeurIPS 2014
    [2]: Chaudhari et al., “Entropy-SGD: Gradientenabstieg in breite Täler lenken”, ICLR 2017
    [3]: Li et al., “Visualisierung der Verlustlandschaft von neuronalen Netzen”, NeurIPS 2018
    [4]: Zhang et al., “Zyklische stochastische Gradienten-MCMC für bayesianisches Lernen”, ICML 2020
    [5]: Ghorbani et al., “Untersuchung der Fisher-Informationsmatrix und Verlustlandschaft”, ICLR 2019
    [6]: Liu et al., “SHINE: Shift-invariante Hesse für verbesserten natürlichen Gradientenabstieg”, NeurIPS 2023
    [7]: Biamonte et al., “Quantum Machine Learning for Optimierung”, Nature Quantum 2023
    [8]: Moor et al., “Topologische Analyse von neuronalen Verlustlandschaften”, JMLR 2024
    [9]: Yin et al., “Bio-inspirierter adaptiver natürlicher Gradientenabstieg”, AAAI 2023
    [10]: Wang et al., “Chirurgische Modifikation der Landschaft für tiefes Lernen”, CVPR 2024
    [11]: He et al., “Tiefe Einblicke in Rektifier: Übersteigende menschliche Leistung bei ImageNet-Klassifizierung”, ICCV 2015↩︎