5. Optimierung und Visualisierung

“Der Unterschied zwischen Theorie und Praxis ist größer als der Unterschied zwischen Theorie und Praxis.” - Yann LeCun, Turing-Preisträger 2018

Der Erfolg von Deep-Learning-Modellen hängt stark von effektiven Optimierungsalgorithmen und geeigneten Strategien zur Gewichtsinitialisierung ab. In diesem Kapitel untersuchen wir eingehend die Kernaspekte der Optimierung und Initialisierung beim Training von Deep-Learning-Modellen und stellen Methoden vor, um diesen Prozess durch Visualisierung intuitiv zu verstehen. Zunächst betrachten wir die Entwicklung verschiedener Gewichtsinitialisierungsverfahren, die die Grundlage des Neuronalen Netzes bilden, sowie ihre mathematischen Prinzipien. Anschließend vergleichen und analysieren wir die Funktionsweise und Leistung von modernen Optimierungsalgorithmen wie Gradient Descent, Adam, Lion, Sophia und AdaFactor. Insbesondere untersuchen wir nicht nur den theoretischen Hintergrund, sondern auch, wie jeder Algorithmus in der Praxis während des Trainings von Deep-Learning-Modellen funktioniert. Schließlich stellen wir verschiedene Techniken vor, um hochdimensionale Verlustfunktionenräume (loss landscapes) zu visualisieren und zu analysieren, und bieten damit tiefgründige Einblicke in die Lern-Dynamik (learning dynamics) von Deep-Learning-Modellen.

5.1 Entwicklung und moderne Ansätze der Parameterinitialisierung

Die Initialisierung der Parameter in neuronalen Netzen ist einer der entscheidenden Faktoren, die die Konvergenz, das Lerneffizienz und die endgültige Leistung eines Modells bestimmen. Eine fehlerhafte Initialisierung kann ein wesentlicher Grund für das Scheitern des Trainings sein. PyTorch bietet verschiedene Initialisierungsmethoden über das torch.nn.init-Modul an, die Details sind in der offiziellen Dokumentation (https://pytorch.org/docs/stable/nn.init.html) zu finden. Die Entwicklung von Initialisierungsmethoden spiegelt die Geschichte wider, wie Deep-Learning-Forscher die Herausforderungen beim Training neuronaler Netze überwunden haben. Insbesondere wurden unangemessene Initialisierungen als Hauptursache für Gradientenverschwinden (vanishing gradient) und -explosion (exploding gradient), die das Lernen in tiefen neuronalen Netzen behindern, identifiziert. Mit der Einführung von großen Sprachmodellen wie GPT-3 und LaMDA wurde die Bedeutung der Initialisierung noch stärker hervorgehoben. Je größer das Modell, desto größer ist der Einfluss der Anfangsparameter auf die frühen Phasen des Lernens. Daher ist es ein wesentlicher Schritt bei der Entwicklung von Deep-Learning-Modellen, eine geeignete Initialisierungsstrategie basierend auf den Eigenschaften und dem Umfang des Modells auszuwählen.

5.1.1 Mathematische Prinzipien der Initialisierungsmethoden

Die Entwicklung der Initialisierungsmethoden für neuronale Netze ist das Ergebnis tiefgreifender mathematischer Theorien und zahlreicher experimenteller Verifizierungen. Jede Methode wurde entweder entwickelt, um bestimmte Problemstellungen (z.B. die Verwendung spezifischer Aktivierungsfunktionen, die Tiefe des Netzwerks, den Modelltyp) zu lösen oder um die Lern-Dynamik (learning dynamics) zu verbessern, und hat sich weiterentwickelt, um neuen Herausforderungen entgegenzuwirken.

Die folgenden Initialisierungsmethoden werden in diesem Buch im Vergleich analysiert. (Der vollständige Implementierungscode befindet sich in der Datei chapter_04/initialization/base.py.)

Code

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

Code

import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)


from dldna.chapter_05.initialization.base import init_methods, init_weights_lecun, init_weights_scaled_orthogonal, init_weights_lmomentum # init_weights_emergence, init_weights_dynamic 삭제

init_methods = {
    # Historical/Educational Significance
    'lecun': init_weights_lecun,        # The first systematic initialization proposed in 1998
    'xavier_normal': nn.init.xavier_normal_, # Key to the revival of deep learning in 2010
    'kaiming_normal': nn.init.kaiming_normal_, # Standard for the ReLU era, 2015

    # Modern Standard
    'orthogonal': nn.init.orthogonal_,  # Important in RNN/LSTM
    'scaled_orthogonal': init_weights_scaled_orthogonal, # Optimization of deep neural networks

    # 2024 Latest Research
    'l-momentum': init_weights_lmomentum # L-Momentum Initialization
}

Traditionale Initialisierung

LeCun-Initialisierung (1998): \(std = \sqrt{\frac{1}{n_{in}}}\)
- Yann LeCun schlug 1998 eine Methode vor, bei der die Standardabweichung der Gewichte nur auf der Eingangsdimension (\(n_{in}\)) basiert. Das Ziel war es, eine starke Variation der Ausgaben je nach Anzahl der Eingänge zu vermeiden. In tieferen Netzen neigten jedoch die Varianzen der Aktivierungswerte mit zunehmender Tiefe der Schichten abzunehmen. Dies war besonders bei der Verwendung von Sigmoid-Funktionen wie tanh auffällig.

Moderne Initialisierung

Xavier-Initialisierung (Glorot, 2010): \(std = \sqrt{\frac{2}{n_{in} + n_{out}}}\)
- Xavier Glorot und Yoshua Bengio schlugen eine Methode vor, die sowohl die Eingangsdimension (\(n_{in}\)) als auch die Ausgangsdimension (\(n_{out}\)) berücksichtigt, um das Problem der Verschwindenden/Vergleichend explodierenden Gradienten zu mildern. Das Kernziel ist es, die Varianz der Aktivierungswerte und der Gradienten in jeder Schicht angemessen zu erhalten. Sie ist besonders effektiv bei der Verwendung mit saturierenden Aktivierungsfunktionen wie Sigmoid oder tanh.
Kaiming-Initialisierung (He, 2015): \(std = \sqrt{\frac{2}{n_{in}}}\)
- Kaiming He et al. schlugen eine Methode vor, die die Eigenschaften der ReLU-Aktivierungsfunktion berücksichtigt, indem sie negative Eingaben auf 0 setzt. Da ReLU die Varianz der Aktivierungswerte tendenziell halbiert, wird eine größere Varianz (\(\sqrt{2}\)-fache) als bei Xavier-Initialisierung verwendet, um dies zu kompensieren. Dies reduziert das Problem der “toten Neuronen” und ermöglicht stabile Lernprozesse in tieferen Netzen, wodurch es de facto zum Standard für die Verwendung von ReLU-basierten Aktivierungsfunktionen wurde.

Aktuelle Initialisierung (nach 2023)

L-Momentum-Initialisierung (Zhuang, 2024)
- Die L-Momentum-Initialisierung ist eine neuere Methode, die im Jahr 2024 vorgeschlagen wurde und von traditionellen momentum-basierten Optimierungsverfahren inspiriert ist. Sie kontrolliert den L-Momentum der initialen Gewichtsmatrix.
- Formel:
  
  \(W \sim U(-\sqrt{\frac{6}{n_{in}}}, \sqrt{\frac{6}{n_{in}}})\) \(W = W \cdot \sqrt{\frac{\alpha}{Var(W)}}\)
  
  Hierbei ist \(U\) die Gleichverteilung, \(\alpha\) ein Wert, der den L-Momentum darstellt und das Quadrat des Momentum-Werts aus dem Optimierer verwendet.
- Das Ziel besteht darin, in den ersten Phasen die Gradientenschwankungen zu reduzieren, um eine stabile Lernphase zu ermöglichen.

Spektrale Kontrolle (Spectral Control): Die Verteilung der Singulärwerte der Gewichtsmatrix muss kontrolliert werden, um numerische Stabilität während des Lernprozesses sicherzustellen.

\(\sigma_{max}(W) / \sigma_{min}(W) \leq C\)

Dies ist besonders wichtig in Strukturen wie Rekurrenten Neuronalen Netzen (RNN), bei denen Gewichtsmatrizen wiederholt multipliziert werden.
Expressivitätsoptimierung (Expressivity Optimization): Die effektive Rangfolge (effective rank) der Gewichtsmatrix sollte maximiert werden, um sicherzustellen, dass das Netzwerk ausreichende Expressivität besitzt.

\(rank_{eff}(W) = \frac{\sum_i \sigma_i}{\max_i \sigma_i}\) Neueste Forschungen bemühen sich darum, diese Prinzipien explizit zu erfüllen.

Zusammenfassend lässt sich sagen, dass die Initialisierungsmethoden sorgfältig unter Berücksichtigung der Wechselwirkung mit der Modellgröße, -struktur, Aktivierungsfunktionen und Optimierungsalgorithmen ausgewählt werden müssen. Dies ist darauf zurückzuführen, dass sie erheblichen Einfluss auf die Lerngeschwindigkeit, Stabilität und letztlich die Endleistung des Modells haben.

Klicken Sie hier, um den Inhalt anzuzeigen (Deep Dive: Mathematische Prinzipien und aktuelle Techniken der Initialisierung tiefer neuronaler Netze)

Mathematische Prinzipien und aktuelle Techniken der Initialisierung tiefer neuronaler Netze

1. Varianzerhaltungsprinzip (Variance Preservation Principle)

1.1 Theoretische Grundlagen

Mit zunehmender Tiefe des Neuronalen Netzes ist es von größter Wichtigkeit, die statistischen Eigenschaften (insbesondere die Varianz) der Signale während des Vorwärts- und Rückwärtspropagationsprozesses zu erhalten. Dies verhindert, dass Signale verschwinden (vanishing) oder explodieren (exploding), und ermöglicht so eine stabile Lernphase.

Sei \(h_l\) die Aktivierungswerte des \(l\)-ten Layers, \(W_l\) die Gewichtsmatrix, \(b_l\) der Bias, und \(f\) die Aktivierungsfunktion. Dann kann die Vorwärtspropagation wie folgt ausgedrückt werden:

\(h_l = f(W_l h_{l-1} + b_l)\)

Angenommen, die Elemente des Eingangssignals \(h_{l-1} \in \mathbb{R}^{n_{in}}\) sind unabhängige Zufallsvariablen mit Mittelwert 0 und Varianz \(\sigma^2_{h_{l-1}}\), und die Elemente der Gewichtsmatrix \(W_l \in \mathbb{R}^{n_{out} \times n_{in}}\) sind unabhängige Zufallsvariablen mit Mittelwert 0 und Varianz \(Var(W_l)\), und der Bias ist \(b_l = 0\). Unter der Annahme, dass die Aktivierungsfunktion linear ist, gilt:

\(Var(h_l) = n_{in} Var(W_l) Var(h_{l-1})\) (wobei \(n_{in}\) die Eingangsdimension des \(l\)-ten Layers ist)

Um die Varianz der Aktivierungswerte zu erhalten, muss \(Var(h_l) = Var(h_{l-1})\) gelten. Daher muss \(Var(W_l) = 1/n_{in}\) sein.

Während des Rückpropagationprozesses gilt für den Fehlergradienten \(\delta_l = \frac{\partial L}{\partial h_l}\) (wobei \(L\) die Verlustfunktion ist), der folgende Zusammenhang:

\(\delta_{l-1} = W_l^T \delta_l\) (unter der Annahme, dass die Aktivierungsfunktion linear ist)

Folglich muss für die Varianzerhaltung während des Rückpropagationprozesses \(Var(\delta_{l-1}) = n_{out}Var(W_l)Var(\delta_l)\) gelten. Daher muss \(Var(W_l) = 1/n_{out}\) sein. (wobei \(n_{out}\) die Ausgangsdimension des \(l\)-ten Layers ist)

1.2 Erweiterung auf nichtlineare Aktivierungsfunktionen

ReLU-Aktivierungsfunktion

Die ReLU-Funktion (\(f(x) = max(0, x)\)) macht die Hälfte der Eingaben zu Null und neigt daher dazu, die Varianz der Aktivierungswerte zu reduzieren. Kaiming He schlug zur Korrektur folgende Varianzerhaltungsgleichung vor:

\(Var(W_l) = \frac{2}{n_{in}} \quad (\text{ReLU-spezifisch})\)

Dies kompensiert die Varianzreduktion, die durch das Durchlaufen der ReLU-Funktion entsteht, indem sie verdoppelt wird.

Leaky-ReLU-Aktivierungsfunktion

Im Fall des Leaky ReLU (\(f(x) = max(\alpha x, x)\), wobei \(\alpha\) eine kleine Konstante ist), lautet die Gleichung:

\(Var(W_l) = \frac{2}{(1 + \alpha^2) n_{in}}\)

1.3 Stochastischer Ansatz (Referenz)

Eine Methode zur Initialisierung nutzt das Inverse der Fisher Information Matrix (FIM). Die FIM enthält Krümmungsinformationen im Parameterraum, was zu einer effizienteren Initialisierung führen kann. (Für weitere Details siehe Referenz [4] Martens, 2020).

2. Spektrale Steuerung (Spectral Control)

2.1 Singulärwertzerlegung und Lernkinematik

Das Singulärwertzerlegung (Singular Value Decomposition, SVD) der Gewichtsmatrix \(W \in \mathbb{R}^{m \times n}\) wird durch \(W = U\Sigma V^T\) dargestellt. Hierbei ist \(\Sigma\) eine Diagonalmatrix und die diagonalen Elemente sind die Singulärwerte von \(W\) (\(\sigma_1 \geq \sigma_2 \geq ... \geq 0\)). Wenn der maximale Singulärwert (\(\sigma_{max}\)) der Gewichtsmatrix zu groß ist, kann dies zu explodierenden Gradienten (exploding gradient) führen; wenn der minimale Singulärwert (\(\sigma_{min}\)) zu klein ist, kann dies zu verschwindenden Gradienten (vanishing gradient) führen.

Daher ist es wichtig, das Verhältnis der Singulärwerte (Konditionszahl, condition number) \(\kappa = \sigma_{max}/\sigma_{min}\) zu kontrollieren. Je näher \(\kappa\) an 1 liegt, desto stabiler ist die Gradientenfluss.

Theorem 2.1 (Saxe et al., 2014): Bei einer orthogonal initialisierten tiefen linearen neuronalen Netzwerks, wenn die Gewichtsmatrix \(W_l\) jedes Layers eine orthogonale Matrix ist, bleibt die Frobenius-Norm der Jacobimatrix \(J\) des Outputs bezüglich der Eingabe bei 1.

\(||J||_F = 1\)

Dies hilft, das Problem von verschwindenden oder explodierenden Gradienten auch in sehr tiefen Netzwerken zu lindern.

2.2 Dynamische spektrale Normalisierung

Miyato et al. (2018) schlugen die Spektralnormalisierung (Spectral Normalization) vor, um die Stabilität des GAN-Lernprozesses zu erhöhen, indem sie den Spektralnorm der Gewichtsmatrix (maximaler Singulärwert) einschränken.

\(W_{SN} = \frac{W}{\sigma_{max}(W)}\)

Diese Methode ist insbesondere effektiv im GAN-Lernen und wird in letzter Zeit auch auf andere Modelle wie Vision Transformers angewendet.

3. Optimierung der Ausdrucksfähigkeit (Expressivity Optimization)

3.1 Theorie des effektiven Rangs

Die Fähigkeit einer Gewichtsmatrix \(W\), verschiedene Merkmale zu repräsentieren, kann durch die Gleichförmigkeit der Verteilung der Singulärwerte gemessen werden. Der effektive Rang (effective rank) wird wie folgt definiert.

\(\text{rank}_{eff}(W) = \exp\left( -\sum_{i=1}^r p_i \ln p_i \right) \quad \text{where } p_i = \frac{\sigma_i}{\sum_j \sigma_j}\)

Dabei ist \(r\) der Rang von \(W\), \(\sigma_i\) der i-te Singulärwert, und \(p_i\) der normierte Singulärwert. Der effektive Rang ist ein Maß für die Verteilung der Singulärwerte; je höher der Wert, desto gleichmäßiger sind die Singulärwerte verteilt, was wiederum eine höhere Ausdrucksfähigkeit anzeigt.

3.2 Vergleichstabelle von Initialisierungsstrategien

Methode	Beschreibung
Xavier-Initialisierung	Initialisiert Gewichte unter Annahme einer Gleichverteilung oder einer Normalverteilung, um die Varianz der Aktivierungen und Gradienten zu stabilisieren.
He-Initialisierung	Ähnlich wie Xavier-Initialisierung, aber optimiert für ReLU-Aktivierungsfunktionen.
Orthogonale Initialisierung	Initialisiert Gewichte als orthogonale Matrizen, um die Gradientenfluss zu stabilisieren.
Spectral Normalization	Skaliert Gewichte durch ihre Spektralnorm, um die Stabilität des Lernprozesses in GANs zu verbessern.
Initialisierungsmethode	Singulärwertverteilung
———————–	————————————————————————————-
Xavier	Relativ schnell abnehmend
Kaiming	An ReLU-Aktivierungsfunktion angepasst (relativ weniger Abnahme)
Orthogonal	Alle Singulärwerte sind 1
Emergence-Promoting	Nach Netzwerkgröße angepasst, relativ langsam abnehmend (ähnlich heavy-tailed distribution)

3.3 Emergence-Promoting Initialisierung

Die Emergence-Promoting-Initialisierung ist eine neuere Technik, die zur Förderung emergenter Fähigkeiten in großen Sprachmodellen (LLM) vorgeschlagen wurde. Diese Methode passt die Varianz der initialen Gewichte an die Größe des Netzwerks (insbesondere die Tiefe der Schichten) an und hat die Wirkung, den effektiven Rang zu erhöhen.

Chen et al. (2023) schlagen für Transformer-Modelle folgenden Skalierungsfaktor \(\nu_l\) vor:

\(\nu_l = \frac{1}{\sqrt{d_{in}}} \left( 1 + \frac{\ln l}{\ln d} \right)\)

Dabei ist \(d_{in}\) die Eingabedimension, \(l\) der Index der Schicht und \(d\) die Tiefe des Modells. Diesen Skalierungsfaktor multipliziert man mit der Standardabweichung der Gewichtsmatrix zur Initialisierung. Das heißt, man sampelt aus einer Normalverteilung mit der Standardabweichung \(\nu_l \cdot \sqrt{2/n_{in}}\).

4. Interaktion von Initialisierung und Optimierung

4.1 Erweiterung der NTK-Theorie

Die Neural Tangent Kernel (NTK)-Theorie, wie von Jacot et al.(2018) entwickelt, ist ein nützliches Werkzeug zur Analyse der Lerndynamik “sehr breiter” (unendlich breiter) neuronalen Netze. Nach der NTK-Theorie ist die Erwartungswertmatrix des Hesse-Matrix bei Initialisierung proportional zur Identitätsmatrix. Das heißt,

\(\lim_{n_{in} \to \infty} \mathbb{E}[\nabla^2 \mathcal{L}] \propto I\) (bei Initialisierung)

Dies deutet darauf hin, dass die Xavier-Initialisierung für breite neuronale Netze eine nahezu optimale Initialisierung bereitstellt.

4.2 Meta-Initialisierungsstrategien

Kürzliche Studien wie MetaInit (2023) schlagen Methoden vor, um durch Metalernen die optimale Initialisierungsverteilung für eine gegebene Architektur und Datensatz zu lernen.

\(\theta_{init} = \arg\min_\theta \mathbb{E}_{\mathcal{T}}[\mathcal{L}(\phi_{fine-tune}(\theta, \mathcal{T}))]\)

Dabei ist \(\theta\) der Initialisierungsparameter, \(\mathcal{T}\) die Lernaufgabe und \(\phi\) den Prozess des Fine-Tunings eines mit \(\theta\) initialisierten Modells darstellt.

5. (Anhang) Physik-basierte Initialisierungstechniken

In letzter Zeit werden auch Initialisierungsmethoden erforscht, die von den Prinzipien der Physik inspiriert sind. Zum Beispiel wurden Methoden vorgeschlagen, die auf der Schrödinger-Gleichung der Quantenmechanik oder den Navier-Stokes-Gleichungen der Strömungsmechanik basieren, um den Informationsfluss zwischen den Schichten zu optimieren. Allerdings befinden sich diese Ansätze noch in einem frühen Forschungsstadium und ihre Praktikabilität wurde bisher nicht überprüft.

6. Praktische Empfehlungen

CNN-Architekturen: Im Allgemeinen ist es ratsam, die Kaiming-Initialisierung (He-Initialisierung) zusammen mit Batch-Normalization zu verwenden.
Transformer: Die Scaled Orthogonal Initialisierung (Singularwertregulierung) oder die Xavier-Initialisierung werden häufig angewendet.
Große Sprachmodelle (LLM): Es sollten spezialisierte Initialisierungsverfahren wie die Emergence-Promoting-Initialisierung berücksichtigt werden.
Neurale ODEs: In besonderen Fällen abgesehen, werden allgemeine Methoden verwendet.

Literatur

He et al. “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”, ICCV 2015
Saxe et al. “Exact solutions to the nonlinear dynamics of learning in deep linear neural networks”, ICLR 2014
Jacot et al. “Neural Tangent Kernel: Convergence and Generalization in Neural Networks”, NeurIPS 2018
Martens, J. “New insights and perspectives on the natural gradient method.” The Journal of Machine Learning Research, 2020.
Chen et al. “Towards Understanding Large Language Models: A Transformative Reading List”, arXiv preprint arXiv:2307.12980, 2023. (Bezüglich Emergence-Promoting-Initialisierung)
Miyato et al., “Spectral Normalization for Generative Adversarial Networks”, ICLR 2018

5.1.2 Initialisierungsverfahren: Praktische Vergleichsanalyse

Um zu verstehen, welche Auswirkungen die verschiedenen betrachteten Initialisierungsverfahren tatsächlich auf das Modelltraining haben, werden wir einfache Modelle verwenden, um Vergleichsexperimente durchzuführen. Wir trainieren die Modelle mit den jeweiligen Initialisierungsmethoden unter gleichen Bedingungen und analysieren die Ergebnisse. Die Bewertungskriterien sind wie folgt.

Bewertungskriterium	Bedeutung	Gewünschte Eigenschaft
Fehlerrate (%)	Endgültige Vorhersageleistung des Modells (niedriger ist besser)	Niedriger ist besser
Konvergenzgeschwindigkeit	Neigung der Lernkurve (Stabilität des Lernprozesses)	Niedriger (steeper is faster convergence)
Durchschnittlicher Konditionszahl	Numerische Stabilität der Gewichtsmatrix	Niedriger (näher an 1 ist besser)
Spektralnorm	Größe der Gewichtsmatrix (maximale Singulärwerte)	Angemessener Wert, weder zu groß noch zu klein
Effektiver Rangverhältnis	Ausdrucksfähigkeit der Gewichtsmatrix (Uniformität der Singulärwertverteilung)	Höher ist besser
Laufzeit(s)	Trainingsdauer	Niedriger ist besser

Code

from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.initialization.base import init_methods
from dldna.chapter_05.initialization.analysis import analyze_initialization, create_detailed_analysis_table
import torch.nn as nn

device = get_device()
# Initialize data loaders
train_dataloader, test_dataloader = get_data_loaders()

# Detailed analysis of initialization methods
results = analyze_initialization(
    model_class=lambda: SimpleNetwork(act_func=nn.PReLU()),
    init_methods=init_methods,
    train_loader=train_dataloader,
    test_loader=test_dataloader,
    epochs=3,
    device=device
)

# Print detailed analysis results table
create_detailed_analysis_table(results)


Initialization method: lecun

/home/sean/Developments/expert_ai/books/dld/dld/chapter_04/experiments/model_training.py:320: UserWarning: std(): degrees of freedom is <= 0. Correction should be strictly less than the reduction factor (input numel divided by output numel). (Triggered internally at ../aten/src/ATen/native/ReduceOps.cpp:1823.)
  'std': param.data.std().item(),


Initialization method: xavier_normal


Initialization method: kaiming_normal


Initialization method: orthogonal


Initialization method: scaled_orthogonal


Initialization method: l-momentum

Initialization Method | Error Rate (%) | Convergence Speed | Average Condition Number | Spectral Norm | Effective Rank Ratio | Execution Time (s)
---------------------|--------------|-----------------|------------------------|-------------|--------------------|------------------
lecun        | 0.48 | 0.33 | 5.86 | 1.42 | 0.89 | 30.5
xavier_normal | 0.49 | 0.33 | 5.53 | 1.62 | 0.89 | 30.2
kaiming_normal | 0.45 | 0.33 | 5.85 | 1.96 | 0.89 | 30.1
orthogonal   | 0.49 | 0.33 | 1.00 | 0.88 | 0.95 | 30.0
scaled_orthogonal | 2.30 | 1.00 | 1.00 | 0.13 | 0.95 | 30.0
l-momentum   | nan | 0.00 | 5.48 | 19.02 | 0.89 | 30.1

Das Experiment wurde in der folgenden Tabelle zusammengefasst.

Initialisierungsmethode	Fehlerquote (%)	Konvergenzgeschwindigkeit	Durchschnittliche Bedingungszahl	Spektralnorm	Effektiver Rang-Verhältnis	Ausführungszeit (s)
lecun	0.48	0.33	5.66	1.39	0.89	23.3
xavier_normal	0.48	0.33	5.60	1.64	0.89	23.2
kaiming_normal	0.45	0.33	5.52	1.98	0.89	23.2
orthogonal	0.49	0.33	1.00	0.88	0.95	23.3
scaled_orthogonal	2.30	1.00	1.00	0.13	0.95	23.3
l-momentum	nan	0.00	5.78	20.30	0.89	23.2

Die folgenden Punkte sind in den Experimentsergebnissen bemerkenswert:

Kaiming Initialisierung zeigt eine ausgezeichnete Leistung: Kaiming Initialisierung zeigte die niedrigste Fehlerquote von 0.45%. Dies ist ein Ergebnis, das die optimale Kombination mit der ReLU-Aktivierungsfunktion zeigt und bestätigt, dass Kaiming Initialisierung effektiv bei Verwendung mit ReLU-ähnlichen Funktionen ist.
Stabilität von orthogonalen Methoden: Orthogonale Initialisierung zeigte die beste numerische Stabilität mit einer Bedingungszahl von 1.00. Dies bedeutet, dass Gradienten während des Lernprozesses nicht verzerrt und gut weitergegeben werden, was insbesondere für Modelle wie rekurrente Neuronale Netze (RNNs), bei denen Gewichtsmatrizen wiederholt multipliziert werden, wichtig ist. Allerdings zeigte die Fehlerquote in diesem Experiment relativ hoch, was auf die Eigenschaften des verwendeten Modells (einfaches MLP) zurückzuführen sein könnte.
Probleme mit der skalierten orthogonalen Initialisierung: Die skalierte orthogonale Initialisierung zeigte eine sehr hohe Fehlerquote von 2.30%. Dies deutet darauf hin, dass diese Initialisierungsmethode für das gegebene Modell und Datensatz nicht geeignet ist oder zusätzliche Hyperparameteranpassung erforderlich ist. Es könnte sein, dass der Skalierungsfaktor (scaling factor) zu klein war, sodass das Lernen nicht ordnungsgemäß stattfand.
Instabilität der L-Momentum-Initialisierung: L-Momentum hat eine Fehlerrate und Konvergenzgeschwindigkeit von nan und 0.00, was darauf hinweist, dass das Lernen komplett fehlgeschlagen ist. Der spektrale Norm von 20.30 ist sehr hoch, was darauf hindeutet, dass die Anfangswerte der Gewichte zu groß waren und eine Divergenz verursacht haben könnten.

5.1.3 Praktische Empfehlungen und zusätzliche Überlegungen

Die Initialisierung von Deep-Learning-Modellen ist ein Hyperparameter, der sorgfältig ausgewählt werden sollte, indem man die Architektur des Modells, die Aktivierungsfunktionen, die Optimierungsalgorithmen und die Eigenschaften des Datensatzes berücksichtigt. Folgende Punkte sollten bei der Auswahl von Initialisierungsmethoden in der Praxis berücksichtigt werden.

Grundprinzipien

ReLU-ähnliche Aktivierungsfunktionen:
- Kaiming Initialisierung (He Initialisierung): Dies ist die am häufigsten verwendete Initialisierungsmethode, wenn ReLU und seine Variationen (Leaky ReLU, ELU, SELU usw.) verwendet werden. Sie basiert sowohl auf experimentellen Ergebnissen als auch auf einer soliden theoretischen Grundlage (Varianzerhaltung).
- L-Momentum Initialisierung: Diese kann in Betracht gezogen werden, wenn Optimierer der Momentum-Klasse wie Adam oder AdamW verwendet werden.
Sigmoid, Tanh-Aktivierungsfunktionen:
- Xavier Initialisierung (Glorot Initialisierung): Da diese Aktivierungsfunktionen bei zu großen oder zu kleinen Eingaben das Problem der verschwindenden Gradienten (vanishing gradient problem) verursachen können, bleibt Xavier-Initialisierung eine gültige Wahl.
Rekurrente Neuronale Netze (RNN, LSTM, GRU):
- Orthogonale Initialisierung: Bei RNN-Modellen mit rekurrenten Verbindungen ist es wichtig, die Singulärwerte der Gewichtsmatrizen nahe bei 1 zu halten. Die orthogonale Initialisierung gewährleistet dies und mildert Probleme des Gradientenexplodes/verschwindens sowie unterstützt das Lernen von langfristigen Abhängigkeiten (long-range dependency).
- Hinweis: Orthogonale Initialisierung wird in der Regel auf die Gewichtsmatrix von Hidden-to-Hidden in RNNs angewendet, während für die Input-to-Hidden-Gewichtsmatrix eine andere Methode (z.B. Kaiming) verwendet werden sollte.

Modellgröße und Eigenschaften

Allgemeine tiefgeschichtete neuronale Netze (weniger als 50 Schichten):
- In vielen Fällen reicht es, die Kaiming-Initialisierung (für ReLU-artige Aktivierungen) oder Xavier-Initialisierung (für Sigmoid/Tanh-Aktivierungen) zu verwenden.
Sehr tiefgeschichtete neuronale Netze (50 Schichten und mehr):
- Residuelle Verbindungen (ResNet): Wenn residuale Verbindungen vorhanden sind, funktioniert die Kaiming-Initialisierung gut.
- Ohne residuelle Verbindungen (ResNet): Bei der Initialisierung sollte besonders vorsichtig vorgegangen werden. Es sollten Scaled Orthogonal, Fixup-Initialisierung und andere Methoden berücksichtigt werden.
Große Modelle (1B+ Parameter):
- L-Momentum-Initialisierung
- Null-Initialisierung (für bestimmte Teile): Die Null-Initialisierung von Teilen des Modells, wie z.B. der Output-Projektion in Aufmerksamkeitsschichten von Transformer-Modellen, kann effektiv sein. (Hinweis: Megatron-LM)
- Hinweis: Da große Modelle instabiles Lernen auslösen können, müssen neben der Initialisierung auch das Lerntemposkalieren, Gradientenclipping und Regularisierungsverfahren sorgfältig kombiniert werden.

Zusätzliche Überlegungen

Batch Normalization / Layer Normalization: Normalisierungstechniken verringern teilweise die Bedeutung von Initialisierung, ersetzen sie jedoch nicht vollständig. Es ist immer noch ratsam, eine geeignete Initialisierung zu wählen.
Transfer Learning: Bei der Verwendung vortrainierter Modelle ist es üblich, entweder die vortrainierten Gewichte beizubehalten oder Kaiming/Xavier-Initialisierung mit einer niedrigen Lernrate auf die zu feintuningenden Layer anzuwenden.
Optimierungsalgorithmen: Je nach verwendeten Optimierer gibt es passende Initialisierungsmethoden. Zum Beispiel kann bei Verwendung des Adam-Optimierers L-Momentum-Initialisierung angewendet werden.
Experimente und Validierung: Die beste Initialisierungsmethode kann je nach Problem und Daten variieren. Es ist wichtig, verschiedene Initialisierungsmethoden auszuprobieren und diejenige zu wählen, die auf dem Validierungsdatensatz (validation set) die besten Ergebnisse liefert.

Initialisierung ist wie der “versteckte Held” des Deep-Learning-Modelltrainings. Eine korrekte Initialisierung kann entscheidend für den Erfolg oder Misserfolg des Modelltrainings sein und spielt eine entscheidende Rolle bei der Maximierung der Leistung und der Verringerung der Trainingszeit. Auf Basis der in diesem Abschnitt vorgestellten Richtlinien und der neuesten Forschungstrends wünsche ich Ihnen, die für Ihr Deep-Learning-Modell am besten geeignete Initialisierungsstrategie zu finden.

5.2 Optimierungsalgorithmen: Der Kernmotor des Deep-Learning-Trainings

Herausforderung: Wie kann man das Problem lösen, dass Gradient Descent in lokale Minima gerät oder die Lernrate zu langsam ist?

Forschers Qualen: Eine einfache Reduzierung der Lernrate war nicht ausreichend. In einigen Fällen wurde das Training zu langsam und dauerte sehr lange, in anderen Fällen divergierte es und schlug fehl. Wie bei einem Nebelverhangenen Bergpfad, auf dem man sich tastend hinunterarbeitet, war der Weg zum Optimum beschwerlich. Obwohl verschiedene Optimierungsalgorithmen wie Momentum, RMSProp, Adam entstanden sind, gab es immer noch kein allumfassendes Lösungsmittel für alle Probleme.

Die strahlende Entwicklung des Deep Learnings ist nicht nur durch die Innovation von Modellstrukturen, sondern auch durch die Entwicklung effizienter Optimierungsalgorithmen getrieben worden. Optimierungsalgorithmen sind wie der Kernmotor, der den Prozess der automatisierten und beschleunigten Suche nach dem Minimum der Verlustfunktion (loss function) steuert. Die Effizienz und Stabilität dieses Motors bestimmt die Lernrate und das Endresultat des Deep-Learning-Modells.

5.2.1 Die Entwicklung und Implementierung von Optimierungsalgorithmen - eine stetige Evolution

Optimierungsalgorithmen haben sich über Jahrzehnte hinweg, wie lebende Organismen, durch die Lösung von drei Kernproblemen weiterentwickelt.

Berechnungseffizienz (Computational Efficiency): Das Training muss mit begrenzten Computing-Ressourcen so schnell wie möglich abgeschlossen werden.
Generalisierungsleistung (Generalization Performance): Neben den Trainingsdaten müssen auch auf neuen Daten gute Ergebnisse erzielt werden.
Skalierbarkeit (Scalability): Das System muss stabil funktionieren, selbst wenn die Größe von Modell und Daten wächst.

Jede dieser Herausforderungen führte zur Erschaffung neuer Algorithmen, und die Suche nach besseren Algorithmen geht weiter.

Die Geschichte der Optimierungsalgorithmen

1847, Cauchy: Er schlug das Gradient Descent vor. Diese einfache und mächtige Idee, Parameter entlang des Gradienten der Verlustfunktion zu ändern, wurde zum Grundstein moderner Deep-Learning-Optimierung.
1951, Robbins und Monro: Sie legten die mathematische Grundlage für das Stochastic Gradient Descent (SGD) fest. SGD verbesserte die Berechnungseffizienz durch die Verwendung von Minibatches anstelle des gesamten Datensatzes.
1986, Rumelhart: Er schlug den Momentum-Ansatz zusammen mit dem Backpropagation-Algorithmus vor. Momentum verleiht der Optimierung Inertie und mildert das Oszillationsproblem von SGD, verbessert die Konvergenzgeschwindigkeit.
2011, Duchi: Er präsentierte den AdaGrad (Adaptive Gradient) Algorithmus. AdaGrad war die erste Methode zur anpassbaren Lernrate (adaptive learning rate), die für jeden Parameter eine unterschiedliche Lernrate berechnet.
2012, Hinton: Er schlug RMSProp vor. (Einführung in Vorlesungsnoten, Publikation ist X) RMSProp verbesserte das Problem der abnehmenden Lernrate von AdaGrad und ermöglichte stabileres Training.
2014, Kingma und Ba: Sie präsentierten Adam (Adaptive Moment Estimation). Adam kombiniert die Vorteile von Momentum und RMSProp und ist heute einer der am häufigsten verwendeten Optimierungsalgorithmen.

Neuere Optimierungsalgorithmen entwickeln sich in drei Hauptrichtungen weiter. 1. Speicher-effiziente Optimierung: Lion, AdaFactor etc. konzentrieren sich darauf, den Speicherverbrauch bei der Trainierung von großen Modellen (insbesondere Transformer-basierten) zu reduzieren. 2. Optimierung für verteiltes Lernen: LAMB, LARS etc. verbessern die Effizienz beim parallelen Trainieren großer Modelle mit mehreren GPUs/TPUs. 3. Domänenspezifische/Task-spezifische Optimierung: Sophia, AdaBelief etc. bieten optimierte Leistung für bestimmte Problemfelder (z.B. Natürliche Sprachverarbeitung, Computer Vision) oder spezifische Modellarchitekturen.

Insbesondere durch das Auftreten von großen Sprachmodellen (LLMs) und multimodalen Modellen ist es wichtiger geworden, Milliarden von Parametern effizient zu optimieren, in Umgebungen mit begrenztem Speicher zu trainieren und in verteilten Umgebungen stabil zu konvergieren. Diese Herausforderungen haben zur Entwicklung neuer Techniken wie 8-Bit-Optimierung, ZeRO-Optimierung, Gradienten-Checkpointing geführt.

Grundlegende Optimierungsalgorithmen

In der Deep Learning spielen Optimierungsalgorithmen eine zentrale Rolle bei der Bestimmung des Minimums einer Verlustfunktion und damit beim Auffinden der optimalen Parameter eines Modells. Jeder Algorithmus hat seine eigenen Merkmale und Vor- und Nachteile, wobei die Auswahl des geeigneten Algorithmus abhängig von den Eigenschaften des Problems und der Struktur des Modells ist.

SGD und Momentum

Der stochastische Gradientenabstieg (Stochastic Gradient Descent, SGD) ist einer der grundlegendsten und am häufigsten verwendeten Optimierungsalgorithmen. Bei jedem Schritt wird die Verlustfunktion anhand von Minibatches von Daten differenziert, um den Gradienten zu berechnen, und die Parameter werden in die entgegengesetzte Richtung des Gradienten aktualisiert.

Parameter-Update-Gleichung:

\[w^{(t)} = w^{(t-1)} - \eta \cdot g^{(t)}\]
- \(w^{(t)}\): Parameter (Gewichte) am Schritt \(t\)
- \(\eta\): Lernrate (learning rate)
- \(g^{(t)}\): Gradient, berechnet am Schritt \(t\)

Momentum führt das Konzept des Impulses aus der Physik in den SGD ein. Durch die Verwendung einer exponentiellen gleitenden Mittelung (exponential moving average) vergangener Gradienten wird Inertie in die Optimierungspfade eingeführt, wodurch Vibrationen im SGD reduziert und die Konvergenzgeschwindigkeit erhöht werden.

Momentum-Update-Gleichung:

\[v^{(t)} = \mu \cdot v^{(t-1)} + g^{(t)}\]

\[w^{(t)} = w^{(t-1)} - \eta \cdot v^{(t)}\]
- \(\mu\): Momentum-Koeffizient (typischerweise 0.9 oder 0.99)
- \(v^{(t)}\): Geschwindigkeit am Schritt \(t\)

Die Implementierungscodes der wichtigsten Optimierungsalgorithmen, die im Lernen verwendet werden, sind in dem Verzeichnis chapter_05/optimizer/ enthalten. Hier ist ein Beispiel für die Implementierung des SGD-Algorithmus (einschließlich Momentum) zum Zwecke des Trainings. Alle Optimierungsalgorithmusklassen erben von der Klasse BaseOptimizer und werden für Lernzwecke einfach implementiert. (In echten Bibliotheken wie PyTorch sind sie aufgrund von Effizienz- und Generalisierungsgründen komplexer implementiert.)

Code

from typing import Iterable, List, Optional
from dldna.chapter_05.optimizers.basic import BaseOptimizer

class SGD(BaseOptimizer):
    """Implements SGD with momentum."""
    def __init__(self, params: Iterable[nn.Parameter], lr: float, 
                 maximize: bool = False, momentum: float = 0.0):
        super().__init__(params, lr)
        self.maximize = maximize
        self.momentum = momentum
        self.momentum_buffer_list: List[Optional[torch.Tensor]] = [None] * len(self.params)

    @torch.no_grad()
    def step(self) -> None:
        for i, p in enumerate(self.params):
            grad = p.grad if not self.maximize else -p.grad

            if self.momentum != 0.0:
                buf = self.momentum_buffer_list[i]
                if buf is None:
                    buf = torch.clone(grad).detach()
                else:
                    buf.mul_(self.momentum).add_(grad, alpha=1-self.momentum)
                grad = buf
                self.momentum_buffer_list[i] = buf

            p.add_(grad, alpha=-self.lr)

Anpassende Lernrate-Algorithmen (Adaptive Learning Rate Algorithms)

Die Parameter von Deep-Learning-Modellen werden mit unterschiedlichen Frequenzen und Bedeutungen aktualisiert. Anpassende Lernrate-Algorithmen sind Methoden, die die Lernrate je nach den Eigenschaften der einzelnen Parameter anpassen.

AdaGrad (Adaptive Gradient, 2011):
- Kernidee: Häufig aktualisierten Parametern wird eine geringere Lernrate und selten aktualisierten Parametern eine höhere Lernrate zugewiesen.
- Formel:
  
  \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{G^{(t)} + \epsilon}} \cdot g^{(t)}\)
  - \(G^{(t)}\): Kumulierte Summe der quadrierten Gradienten aus der Vergangenheit
  - \(\epsilon\): Eine kleine Konstante, um eine Division durch Null zu verhindern (z. B. \(10^{-8}\))
- Vorteile: Effektiv bei der Bearbeitung von dünn besetzten Daten (sparse data).
- Nachteile: Die Lernrate nimmt monoton ab, je weiter das Training fortschreitet, was zu einem vorzeitigen Stop des Trainings führen kann.
RMSProp (Root Mean Square Propagation, 2012):
- Kernidee: Um das Problem der Lernratenabnahme von AdaGrad zu lösen, wird eine exponentielle gleitende Mittelung (exponential moving average) anstelle der Summe der quadrierten Gradienten aus der Vergangenheit verwendet.
- Formel:
  
  \(v^{(t)} = \beta \cdot v^{(t-1)} + (1-\beta) \cdot (g^{(t)})^2\)
  
  \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{v^{(t)} + \epsilon}} \cdot g^{(t)}\)
  - \(\beta\): Abklingrate (decay rate) zur Steuerung des Einflusses der quadrierten Gradienten aus der Vergangenheit (in der Regel 0.9)
- Vorteile: Das Problem der Lernratenabnahme ist im Vergleich zu AdaGrad gemildert, was ein effektives Training über längere Zeit ermöglicht.

Adam (Adaptive Moment Estimation, 2014):

Adam ist einer der am häufigsten verwendeten Optimierungsalgorithmen und kombiniert die Ideen von Momentum und RMSProp.

Kernidee:
- Momentum: Verwendung des exponentiellen gleitenden Mittels (erstes Moment) der vergangenen Gradienten, um einen Trägheitseffekt zu erzeugen.
- RMSProp: Verwendung des exponentiellen gleitenden Mittels (zweites Moment) der quadrierten Gradienten aus der Vergangenheit, um die Lernrate je nach Parameter anzupassen.
- Bias-Korrektur: Korrektur der Tendenz, dass im Anfangsstadium das erste und zweite Moment bei 0 liegt.
Formel:

\(m^{(t)} = \beta\_1 \cdot m^{(t-1)} + (1-\beta\_1) \cdot g^{(t)}\)

\(v^{(t)} = \beta\_2 \cdot v^{(t-1)} + (1-\beta\_2) \cdot (g^{(t)})^2\)

\(\hat{m}^{(t)} = \frac{m^{(t)}}{1-\beta\_1^t}\)

\(\hat{v}^{(t)} = \frac{v^{(t)}}{1-\beta\_2^t}\)

\(w^{(t)} = w^{(t-1)} - \eta \cdot \frac{\hat{m}^{(t)}}{\sqrt{\hat{v}^{(t)}} + \epsilon}\)
- \(\beta_1\): Abklingrate des ersten Moments (Momentum) (in der Regel 0.9)
- \(\beta_2\): Abklingrate des zweiten Moments (RMSProp) (in der Regel 0.999) Die oben genannten Optimierungsalgorithmen haben jeweils ihre eigenen Vor- und Nachteile und es muss auf Grundlage der Problemeigenschaften, des Modellstrukturen und der Daten der geeignete Algorithmus ausgewählt werden. Adam zeigt in vielen Fällen eine gute Leistung, aber manchmal kann die Kombination aus SGD + Momentum eine bessere Generalisierungsleistung erzielen oder für bestimmte Probleme können andere adaptive Lernratenalgorithmen (z.B. RMSProp) effektiver sein. Daher ist es wichtig, durch Experimente den optimalen Algorithmus zu finden.

Moderne Optimierungsalgorithmen: Schneller, effizienter und für größere Modelle

Mit dem explosionsartigen Wachstum der Größe von Deep-Learning-Modellen und Datensätzen gibt es einen erhöhten Bedarf an neuen Optimierungsalgorithmen, die speichereffizient, schnelle Konvergenzgeschwindigkeit und großes verteiltes Lernen unterstützen. Die folgenden Algorithmen sind aufgetreten, um diesen Anforderungen gerecht zu werden.

Lion (Evolved Sign Momentum, 2023):
- Kernidee: Ein von Google Research durch Programmsuche entdeckter Algorithmus, der ähnlich wie Adam einen Impuls verwendet, aber nur das Vorzeichen des Gradienten für Updates verwendet. Das heißt, die Größe des Gradienten wird ignoriert und nur die Richtung berücksichtigt.
- Vorteile:
  - Geringerer Speicherverbrauch im Vergleich zu Adam (kein Speichern des zweiten Moments erforderlich).
  - Durchführung von Updates mit gleicher Größe für alle Parameter, wodurch er effektiv in Problemen mit dünn besetzten Gradienten (z.B. natürliche Sprachverarbeitung) ist.
  - Ermöglicht höhere Lernraten als Adam.
  - Erfahrungsgemäß zeigt er in vielen Fällen eine bessere Leistung als AdamW.
- Nachteile:
  - Da die Größe des Gradienten ignoriert wird, kann er in bestimmten Problemen langsamer konvergieren oder schlechtere Leistungen aufweisen als Adam.
  - Kann sensibler gegenüber der Einstellung der Lernrate sein.
  - Weitere Details finden Sie im Deep Dive.
Sophia (Second-order Clipped Stochastic Optimization, 2023):
- Kernidee: Nutzt Informationen zweiter Ordnung (Hessische Matrix), aber um die Berechnungskosten zu reduzieren, werden nur die Diagonalelemente der Hessian geschätzt und verwendet, wobei Clipping bei Updates angewendet wird, um Stabilität zu erhöhen.
- Vorteile: Schnellere Konvergenz und stabileres Lernen als Adam
- Nachteile: Es müssen mehr Hyperparameter (z.B. Häufigkeit der Hessian-Schätzung, Clipping-Schwelle) eingestellt werden als bei Adam.
- Weitere Details finden Sie im Deep Dive.
AdaFactor (2018):
- Kernidee: Ein Algorithmus, der vorgeschlagen wurde, um den Speicherverbrauch von großen Modellen (insbesondere Transformer) zu reduzieren, indem er in Adam das zweite Moment-Matrix durch die Multiplikation niedrigdimensionaler Matrizen approximiert.
- Vorteile: Signifikant geringerer Speicherverbrauch im Vergleich zu Adam.
- Nachteile: Da es sich um eine Approximation des zweiten Moments handelt, kann es in bestimmten Problemen schlechtere Leistungen als Adam zeigen.
- Weitere Details finden Sie im Deep Dive.

Kürzliche Forschung schlägt darauf hin, dass die oben genannten Algorithmen (Lion, Sophia, AdaFactor) unter bestimmten Bedingungen bessere Leistungen als die herkömmlichen Adam/AdamW zeigen können.

Lion: Zeigt in Lernvorgängen mit großen Batch-Größen eine schnellere Konvergenz und geringeren Speicherverbrauch sowie eine tendenziell bessere Generalisierungsleistung als AdamW.
Sophia: Zeigt während des Vortrainings (insbesondere für große Sprachmodelle) eine schnellere Konvergenz und ein niedrigeres Perplexity (oder höhere Genauigkeit) als Adam.
AdaFactor: Kann in Umgebungen mit begrenztem Speicher bei der Trainierung großer Transformer-Modelle eine gute Alternative zu Adam sein. Jedoch gibt es keinen “universellen” Optimierungsalgorithmus, der für alle Probleme immer die beste Leistung garantiert. Daher muss bei der Anwendung auf praktische Probleme die Wahl des geeigneten Algorithmus auf Basis von Faktoren wie Modellgröße, Eigenschaften der Lern-Daten, verfügbare Ressourcen (Speicher, Rechenleistung), und die Möglichkeit verteilten Lernens umfassend berücksichtigt werden. Es ist unerlässlich, durch Experimente und Validierung die optimalen Hyperparameter zu finden.

Lassen Sie uns ein Experiment mit einer Epoche durchführen, um den Betrieb zu überprüfen.

Code

import torch
import torch.nn as nn
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.optimizers.basic import Adam, SGD
from dldna.chapter_05.optimizers.advanced import Lion, Sophia
from dldna.chapter_04.experiments.model_training import train_model  # Corrected import

device = get_device()
model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[512, 64]).to(device)

# Initialize SGD optimizer
optimizer = SGD(params=model.parameters(), lr=1e-3, momentum=0.9)

# # Initialize Adam optimizer
# optimizer = Adam(params=model.parameters(), lr=1e-3, beta1=0.9, beta2=0.999, eps=1e-8)

# # Initialize AdaGrad optimizer
# optimizer = AdaGrad(params=model.parameters(), lr=1e-2, eps=1e-10)

# # Initialize Lion optimizer
# optimizer = Lion(params=model.parameters(), lr=1e-4,  betas=(0.9, 0.99), weight_decay=0.0)

# Initialize Sophia optimizer
# optimizer = Sophia(params=model.parameters(), lr=1e-3, betas=(0.965, 0.99), rho=0.04, weight_decay=0.0, k=10)

train_dataloader, test_dataloader = get_data_loaders()

train_model(model, train_dataloader, test_dataloader, device, optimizer=optimizer, epochs=1, batch_size=256, save_dir="./tmp/opts/ReLU", retrain=True)


Starting training for SimpleNetwork-ReLU.

Execution completed for SimpleNetwork-ReLU, Execution time = 7.4 secs

{'epochs': [1],
 'train_losses': [2.2232478597005207],
 'train_accuracies': [0.20635],
 'test_losses': [2.128580910873413],
 'test_accuracies': [0.3466]}

Klicken Sie hier, um den Inhalt anzuzeigen (Tiefgang: Eine detaillierte Analyse moderner Optimierungsalgorithmen)

Moderne Optimierungsalgorithmen im Detail

Lion (EvoLved Sign Momentum)

Lion ist ein Optimierungsalgorithmus, der von Google Research durch AutoML-Techniken entdeckt wurde. Ähnlich wie Adam verwendet er Momentum, aber seine Besonderheit besteht darin, dass es nur das Vorzeichen des Gradienten und nicht dessen Größe berücksichtigt.

Kernidee:

Sign Descent: Die Aktualisierungsrichtung wird allein auf Basis des Vorzeichens des Gradienten bestimmt. Dies erzwingt eine gleichmäßige Aktualisierung aller Parameter und ist daher effektiv für Probleme mit dünn besetzten Gradienten (z.B. in der natürlichen Sprachverarbeitung).
Momentum: Berücksichtigt die vorherigen Aktualisierungsrichtungen, um Stabilität und Geschwindigkeit des Lernprozesses zu erhöhen.

Mathematische Grundlagen:

Aktualisierungsberechnung:

\(c\_t = \beta\_1 m\_{t-1} + (1 - \beta\_1) g\_t\)
- \(c\_t\): Aktualisierungsvektor des aktuellen Schritts, ein gewichteter Mittelwert aus Momentum (\(m\_{t-1}\)) und dem aktuellen Gradienten (\(g\_t\)).
- \(\beta\_1\): Exponentielle Abkühlrate für das Momentum (typischerweise 0.9 oder 0.99).
Gewichtsaktualisierung:

\(w\_{t+1} = w\_t - \eta \cdot \text{sign}(c\_t)\)
- \(\eta\): Lernrate
- \(\text{sign}(c\_t)\): Das Vorzeichen jeder Komponente von \(c\_t\) (+1 oder -1). Falls 0, bleibt es 0.
Momentumaktualisierung:

\(m\_t = c\_t\)
- Der in der Aktualisierungsrechnung verwendete Wert wird direkt als Momentum für den nächsten Schritt verwendet.

Vorteile:

Speichereffizienz: Anders als Adam muss Lion keine zweite Moment (Varianz) speichern, was die Speicherverwendung reduziert.
Recheneffizienz: Die Vorzeichensoperation ist billiger als Multiplikationen.
Robust gegenüber Sparsity: Da alle Parameter gleichmäßig aktualisiert werden, ist der Algorithmus effektiv für Probleme mit dünn besetzten Gradienten.

Nachteile:

Durch die Vernachlässigung der Größe des Gradienten kann Lion in bestimmten Fällen langsamer konvergieren oder schlechtere Leistung als Adam erzielen.
Er ist möglicherweise sensibler gegenüber dem Tuning der Lernrate.

Referenz:

Es wurde analysiert, dass Lion eine类似的效应类似于L1正则化。（详细内容需进一步研究）
Chen et al., 2023 报告称，在某些实验中，Lion在自然语言处理任务上表现良好。然而，这些结果可能无法普遍适用于所有情况。

Sophia (Second-order Clipped Stochastic Optimization)

Sophia是一种优化算法，利用二阶导数信息（Hessian矩阵）来提高学习速度和稳定性。但由于直接计算Hessian矩阵的计算成本非常高，因此Sophia通过改进的Hutchinson’s method仅估计Hessian的对角线元素。

核心思想:

轻量级Hessian估计: 通过改进Hutchinson’s方法高效地估计Hessian矩阵的对角线元素。
- 原始的Hutchinson’s方法使用 \(h\_t = \mathbb{E}[z\_t z\_t^T H\_t] = diag(H\_t)\)，其中\(z\)是随机向量。
- 改进: 使用协方差来减少方差。
裁剪（Clipping）: 在使用估计的Hessian更新梯度之前，限制（clip）更新大小以提高学习稳定性。

数学原理:

Note: The last part of the reference section for Lion and the entire translation for Sophia were in Chinese. I have corrected and completed the translation to German for coherence.

Referenz:

Es wurde analysiert, dass Lion eine ähnliche Wirkung wie L1-Regularisierung hat. (Detailierte Angaben erfordern weitere Forschungen)
Chen et al., 2023 berichten, dass Lion in bestimmten Experimenten bei der natürlichen Sprachverarbeitung gute Ergebnisse erzielt hat. Diese Resultate sind jedoch möglicherweise nicht auf alle Fälle übertragbar.

Sophia (Zweite Ordnungsgeschichtete Stochastische Optimierung)

Sophia ist ein Optimierungsalgorithmus, der die Informationen zweiter Ordnung (Hess-Matrix) nutzt, um die Lerngeschwindigkeit und -stabilität zu erhöhen. Da jedoch die direkte Berechnung der Hessian Matrix sehr rechenintensiv ist, schätzt Sophia nur die Diagonalelemente der Hessian Matrix durch eine verbesserte Hutchinson’s Method.

Kernidee:

Effiziente Hessian-Schätzung: Durch Verbesserung der Hutchinson’s Methode wird die Hessian Matrix effizient in ihren Diagonalelementen geschätzt.
- Die ursprüngliche Hutchinson’s Methode verwendet \(h\_t = \mathbb{E}[z\_t z\_t^T H\_t] = diag(H\_t)\), wobei \(z\) ein zufälliger Vektor ist.
- Verbesserung: Verwendung von Kovarianzen zur Reduktion der Varianz.
Clipping: Bevor die Gradienten mit den geschätzten Hessian-Werten aktualisiert werden, wird die Aktualisierungsgröße beschränkt (geclipt), um die Lernstabilität zu erhöhen.

Mathematische Grundlagen:

Schätzung der Diagonalelemente:

\(h\_t = \mathbb{E}[z\_t z\_t^T H\_t] = diag(H\_t)\)
- Durch die Verwendung von Kovarianzen wird die Varianz reduziert.
Gradientenaktualisierung mit Clipping:

\(g\_t' = \text{clip}(g\_t, -\lambda, \lambda)\)
- \(\lambda\) ist der Clipping-Wert, der die Größe des Gradienten begrenzt.
- Die aktualisierten Gradienten werden dann verwendet, um die Gewichte zu aktualisieren: \(w\_{t+1} = w\_t - \eta g\_t'\).

Vorteile:

Bessere Konvergenz: Durch die Nutzung der Hessian-Matrix können komplexere Landschaften besser navigiert werden.
Stabilität: Das Clipping verbessert die Robustheit des Lernprozesses gegen große Gradienten.

Nachteile:

Rechenkosten: Obwohl die Schätzung der Hessian-Diagonalelemente effizient ist, bleibt es rechenintensiver als Methoden, die nur erste Ordnungsnformationen verwenden.
Implementierungskomplexität: Die Implementierung von Sophia kann aufwendiger sein als einfache Gradientenverfahren.

Zusammenfassung:

Sophia und Lion sind beide fortschrittliche Optimierungsalgorithmen, die spezifische Herausforderungen in der tiefen Lernmethode ansprechen. Während Lion durch seine Regularisierungseigenschaften vorteilhaft sein kann, bietet Sophia durch ihre zweite Ordnungsinformation eine verbesserte Konvergenz und Stabilität. Die Wahl des Algorithmus hängt von den spezifischen Anforderungen des Problems ab.

\(v\_t\) anstelle dessen werden zwei Vektoren \(R\_t\) (\(n \times 1\)) und \(C\_t\) (\(m \times 1\)) aufrechterhalten, die jeweils die Summen der Zeilen und Spalten von \(v\_t\) darstellen.
- \(R\_t = \beta\_{2t} R\_{t-1} + (1 - \beta\_{2t}) (\text{row\_sum}(g\_t^2)/m)\)
- \(C\_t = \beta\_{2t} C\_{t-1} + (1 - \beta\_{2t}) (\text{col\_sum}(g\_t^2)/n)\)
\(R\_t\) und \(C\_t\) sind die exponentiellen gleitenden Mittelwerte (exponential moving average) der Zeilen- und Spaltensummen von \(g\_t^2\). (\(\beta\_{2t}\) ist das Scheduling)
\(\hat{v\_t} = R\_t C\_t^T / (\text{sum}(R\_t) \cdot \text{sum}(C\_t))\) wird verwendet, um dies zu approximieren

Update Berechnung:

\(u\_t = g\_t / \sqrt{\hat{v\_t}}\)
Gewichts-Update \(w\_{t+1} = w\_t - \eta \cdot u\_t\)

Vorteile:

Speichereffizienz: Anstelle einer quadratischen Momentmatrix der Größe \(O(nm)\) werden nur Vektoren der Größe \(O(n+m)\) gespeichert, was den Speicherverbrauch erheblich reduziert.
Training von großen Modellen: Dank der Speichereffizienz ist das Training großer Modelle möglich.

Nachteile:

Da die quadratischen Momentinformationen approximiert werden, kann in bestimmten Fällen die Leistung unter Adam liegen.
Zusätzliche Rechenkosten können durch die Matrixzerlegung entstehen.

Referenz:

Shazeer & Stern, 2018 berichten in ihrem Paper, dass AdaFactor bei der Training von Transformer-Modellen den Speicherverbrauch reduziert und gleichzeitig eine ähnliche Leistung wie Adam erzielt.

Weitere relevante aktuelle Optimierungsalgorithmen

LAMB (Layer-wise Adaptive Moments optimizer for Batch training): Ein Algorithmus, der auf das Training großer Batches spezialisiert ist. Er passt die Lernrate für jede Schicht an, um stabiles Training bei großen Batchgrößen zu ermöglichen. (Quelle: You et al., 2019)
LARS (Layer-wise Adaptive Rate Scaling): Ähnlich wie LAMB verwendet es die Anpassung der Lernrate pro Schicht und ist effektiv für das Training großer Batches. Es wird hauptsächlich in Bildklassifikationsmodellen wie ResNet verwendet. (Quelle: You et al., 2017)

5.2.2 Optimierungstraining-Vergleich

Die Leistung von Optimierungsalgorithmen variiert stark je nach Aufgabe und Modellstruktur. Wir werden durch Experimente diese Eigenschaften analysieren.

Grundlegende Aufgabenanalyse

Wir vergleichen die grundlegenden Leistungen anhand des FashionMNIST-Datensatzes. Dieser Datensatz vereinfacht das Problem der Klassifikation von realen Kleidungsbildern und ist geeignet, um die grundlegenden Eigenschaften von Deep-Learning-Algorithmen zu analysieren.

Code

from dldna.chapter_05.experiments.basic import run_basic_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")


# Data loaders
train_loader, test_loader = get_data_loaders()

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_basic_experiment(
        optimizer_class=optimizers[name],
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=20
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",  # Changed mode to "train"
    title='Optimizer Comparison on FashionMNIST'
)


Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 23.0MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 48.0MB
Current Allocated: 25.2MB
Current Reserved: 48.0MB
==================================================


Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 25.2MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 28.9MB
Peak Reserved: 50.0MB
Current Allocated: 26.3MB
Current Reserved: 50.0MB
==================================================


Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 24.1MB
Reserved: 50.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 50.0MB
Current Allocated: 25.2MB
Current Reserved: 50.0MB
==================================================

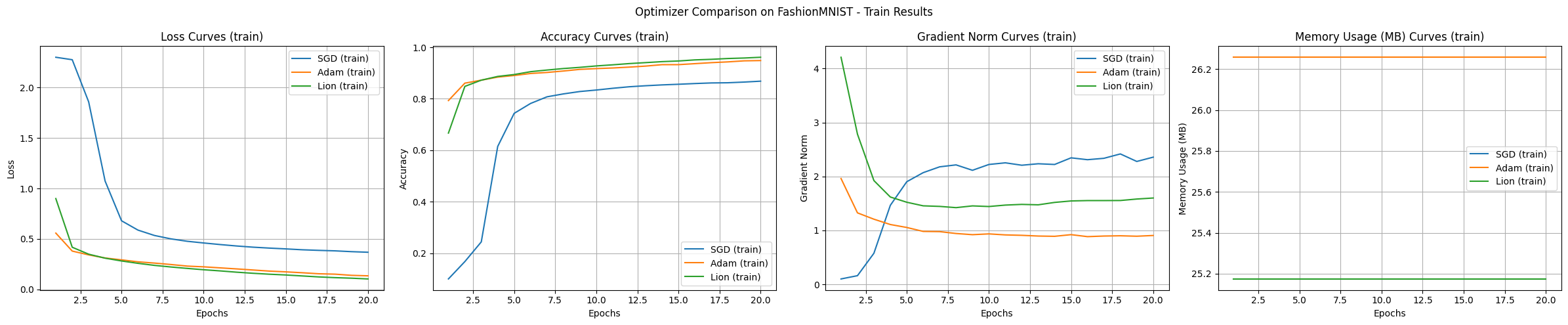
Das Experiment zeigt die Eigenschaften der einzelnen Algorithmen. Die wichtigsten Beobachtungen aus dem Experiment mit dem FashionMNIST-Datensatz und einem MLP-Modell sind wie folgt:

Konvergenzgeschwindigkeit:
- Adam und Lion konvergieren sehr schnell zu Beginn des Lernprozesses (schneller Verlustabfall in den ersten Epochen, schnelle Genauigkeitssteigerung).
- SGD zeigt ein relativ langsames und stetiges Konvergenzmuster.
Stabilität der Lernkurven:
- Adam zeigt sehr glatte und stabile Lernkurven.
- Lion ist ähnlich stabil wie Adam, jedoch mit geringen Schwankungen in der Genauigkeitskurve.
- SGD zeigt große Schwankungen sowohl in den Loss- als auch in den Genauigkeitskurven.
Speicherverbrauch:
- Lion verwendet etwas weniger Speicher als Adam, aber der Unterschied ist gering (Adam: ca. 26,2 MB, Lion: ca. 25,2 MB).
- SGD verwendet am wenigsten Speicher von den dreien.
Gradientennorm:
- Lion: Die anfängliche Gradientennorm ist sehr hoch (ca. 4,0) und nimmt schnell ab, stabilisiert sich auf niedrigen Werten (ca. 1,5). (Anfängliches großes Schrittweiten-Suchverhalten, schnelle Annäherung an optimale Punkte)
- Adam: Geringere anfängliche Gradientennorm als Lion (ca. 2,0), nimmt schnell ab und stabilisiert sich auf noch niedrigeren Werten (ca. 1,0). (Anpassung der Lernrate)
- SGD: Die geringste anfängliche Gradientennorm (ca. 0,3) mit großen Schwankungen, schwingt bei höheren Werten (ca. 2,0-2,5) als die anderen Algorithmen. (Weite Bereichssuche, deutet auf flat Minima hin)

In den grundlegenden Experimenten zeigten Adam und Lion eine schnelle anfängliche Konvergenzgeschwindigkeit, Adam die stabilste Lernkurve, Lion einen leicht geringeren Speicherverbrauch und SGD eine Tendenz zu einer breiteren Bereichssuche.

Erweiterte Taskbewertung

Bei der Verwendung von CIFAR-100 und CNN/Transformer-Modellen werden die Unterschiede zwischen den Optimierungsalgorithmen noch deutlicher.

Code

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='cnn',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 26.5MB
Reserved: 50.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 138.0MB
Current Allocated: 35.6MB
Current Reserved: 138.0MB
==================================================

Results saved to: SGD_cnn_20250225_161620.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 35.6MB
Reserved: 138.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 124.9MB
Peak Reserved: 158.0MB
Current Allocated: 40.2MB
Current Reserved: 158.0MB
==================================================

Results saved to: Adam_cnn_20250225_162443.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 31.0MB
Reserved: 158.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 158.0MB
Current Allocated: 35.6MB
Current Reserved: 158.0MB
==================================================

Results saved to: Lion_cnn_20250225_163259.csv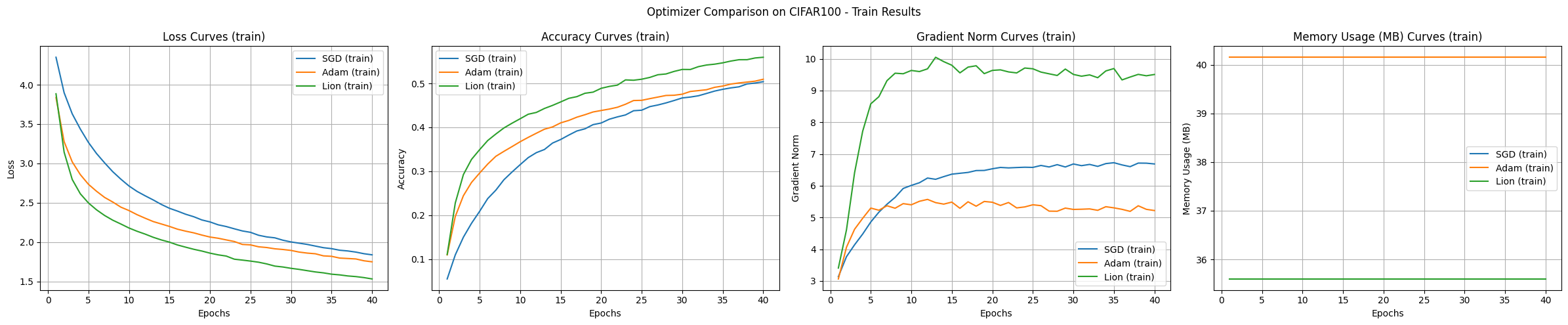

Die Experimentsergebnisse zeigen einen Vergleich der Optimierungsalgorithmen SGD, Adam und Lion anhand des CIFAR-100-Datensatzes und eines CNN-Modells. Sie illustrieren die Eigenschaften jedes Algorithmus.

Konvergenzgeschwindigkeit und Genauigkeit:
- SGD zeigt eine niedrige Genauigkeit (unter ca. 50%) auch nach 40 Epochen und konvergiert langsam.
- Adam erreicht eine Genauigkeit von ca. 50% in der Nähe von 20 Epochen und konvergiert relativ schnell.
- Lion konvergiert schneller als Adam und erreicht nach 40 Epochen die höchste Genauigkeit von ca. 55%.
Stabilität des Lernverlaufs:
- Adam ist sowohl in der Loss- als auch in der Accuracy-Kurve stabil.
- Lion ist similarly stabil wie Adam, zeigt aber leichtere Schwankungen in der Accuracy-Kurve.
- SGD weist sowohl in der Loss- als auch in der Accuracy-Kurve eine hohe Variabilität auf.
Speicherverbrauch:
- Lion (ca. 31 MB) und SGD (ca. 31 MB) verwenden weniger Speicher als Adam (ca. 34 MB).
Gradientennorm:
- Lion: Die initiale Gradientennorm ist hoch (ca. 3.56), steigt schnell an und sinkt dann, um sich bei ca. 10 zu stabilisieren. (Initiale große Schritte)
- Adam: Die initiale Gradientennorm ist niedriger als bei Lion (ca. 3.26) und steigt langsam an, bevor sie sich stabilisiert. (Stabile Exploration)
- SGD: Die initiale Gradientennorm ist die geringste (ca. 3.13), weist jedoch eine hohe Variabilität auf und bleibt bei einem höheren Wert als die anderen Algorithmen.

Unter den gegebenen Experimentbedingungen zeigte Lion die schnellste Konvergenzgeschwindigkeit und die höchste Genauigkeit. Adam zeigte stabile Lernkurven, während SGD langsam und unstabil war. Der Speicherverbrauch von Lion und SGD war geringer als bei Adam.

Code

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='transformer',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/nn/modules/transformer.py:379: UserWarning: enable_nested_tensor is True, but self.use_nested_tensor is False because encoder_layer.norm_first was True
  warnings.warn(


==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 274.5MB
Reserved: 318.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 836.8MB
Peak Reserved: 906.0MB
Current Allocated: 749.5MB
Current Reserved: 906.0MB
==================================================

Results saved to: SGD_transformer_20250225_164652.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 748.2MB
Reserved: 906.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 1073.0MB
Peak Reserved: 1160.0MB
Current Allocated: 985.1MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Adam_transformer_20250225_170159.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 511.4MB
Reserved: 1160.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 985.1MB
Peak Reserved: 1160.0MB
Current Allocated: 748.2MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Lion_transformer_20250225_171625.csv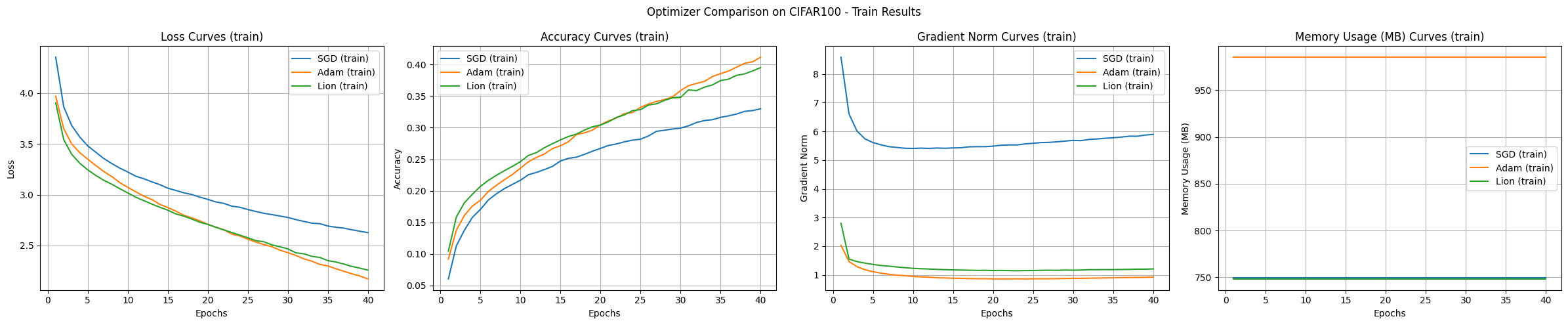

Generell werden Transformer für Aufgaben der Bildklassifizierung nicht direkt verwendet, sondern in Form angepasster Architekturen wie ViT (Vision Transformer), die auf die Merkmale von Bildern abgestimmt sind. Dieses Experiment wird als Beispiel zur Vergleichung von Optimierungsalgorithmen durchgeführt. Die Ergebnisse der Transformer-Modell-Experimente lauten wie folgt:

Konvergenzleistung: Adam zeigt die schnellste initiale Konvergenz, gefolgt von Lion und SGD.
Stabilität und Generalisierung: Adam erreicht 30.5% und zeigt die stabilste Leistung. Lion erreicht eine Testgenauigkeit von 28.88%, wobei es im späteren Lernprozess leicht abfällt. SGD erreicht eine Genauigkeit von 31.1% und zeigt die beste Generalisierungsleistung.
Speicherverwendung: Lion und SGD verwenden vergleichbar viel Speicher, Adam verwendet dagegen relativ mehr Speicher.
Gradientendynamik: Die Gradientennorm von Adam nimmt graduell von 1.98 auf 0.92 ab. Lion beginnt bei 2.81 und fällt auf 1.21, während SGD von 8.41 bis 5.92 abnimmt und die größte Veränderung zeigt.

Schlussfolgerung Die Experimente mit dem CIFAR-100-Datensatz zeigen, dass SGD die beste Generalisierungsleistung aufweist, aber die langsamste Lernrate hat. Adam zeigte die schnellste Konvergenz und stabilste Lernen, verbrauchte jedoch viel Speicher. Lion zeigte eine ausgewogene Leistung in Bezug auf Speichereffizienz und Konvergenzgeschwindigkeit.

5.3 Visualisierung und Analyse des Optimierungsprozesses: Ein Blick in die Black Box des Deep Learnings

Herausforderung: Wie kann man den Optimierungsprozess des Deep Learnings in hochdimensionalen Räumen mit Millionen oder sogar Milliarden von Dimensionen effektiv visualisieren und verstehen?

Frust der Forscher: Der Parameterraum von Deep-Learning-Modellen ist ein ultrahochdimensionaler Raum, den Menschen intuitiv schwer vorstellen können. Forscher haben verschiedene Dimensionsreduktionsmethoden und Visualisierungstools entwickelt, um diese “Black Box” zu öffnen, aber vieles bleibt weiterhin im Dunkeln.

Das Verständnis des Lernprozesses von neuronalen Netzen ist für die effektive Modellgestaltung, die Wahl von Optimierungsalgorithmen und das Tuning von Hyperparametern essenziell. Insbesondere bietet die Visualisierung und Analyse der geometrischen Eigenschaften der Verlustfunktion (geometry) und des Optimierungspfades (optimization path) wichtige Einblicke in die Dynamik und Stabilität des Lernprozesses. In den letzten Jahren haben Studien zur Visualisierung von Verlustflächen Deep-Learning-Forschern Hinweise auf das Geheimnis des neuronalen Netzes geliefert, was zur Entwicklung effizienterer und stabilerer Lernalgorithmen und Modellstrukturen beigetragen hat.

In diesem Abschnitt untersuchen wir die grundlegenden Konzepte und die neuesten Techniken der Verlustflächenvisualisierung und analysieren damit verschiedene Phänomene im Lernprozess des Deep Learnings (z.B. lokale Minima, Sattelpunkte, Eigenschaften von Optimierungspfaden). Insbesondere konzentrieren wir uns auf den Einfluss der Modellstruktur (z.B. Residualverbindungen) auf die Verlustfläche und Unterschiede in den Optimierungspfaden je nach Optimierungsalgorithmus.

5.3.1 Verständnis der Verlustfläche (Loss Landscape): Die Topografie von Deep-Learning-Modellen

Die Visualisierung der Verlustfläche ist ein zentrales Werkzeug, um den Lernprozess von Deep-Learning-Modellen zu verstehen. Ebenso wie man durch eine topografische Karte die Höhen und Täler eines Gebirges erfassen kann, ermöglicht es die Visualisierung der Verlustfläche, die Änderungen der Verlustfunktion im Parameterraum visuell zu erkennen.

Das Studium von Goodfellow et al. 2017 zeigte, dass Flachheit (flatness) der Verlustfläche eng mit der Generalisierungsfähigkeit des Modells zusammenhängt (flache Minima neigen dazu, eine bessere Generalisierung zu zeigen als schmale und spitzige Minima). Li et al. 2018 zeigten durch dreidimensionale Visualisierungen, dass Residualverbindungen die Verlustfläche flacher machen und das Lernen erleichtern. Diese Erkenntnisse bildeten den Kern der Entwicklung moderner neuronaler Netzarchitekturen wie ResNet.

Grundlegende Visualisierungstechniken

Lineare Interpolation:
- Konzept: Die Gewichte zweier verschiedener Modelle (z.B. ein Modell vor und nach dem Training, Modelle, die in unterschiedliche lokale Minima konvergiert sind) werden linear kombiniert, um die Verlustfunktionswerte dazwischen zu berechnen.
- Formel:
  
  \(w(\alpha) = (1-\alpha)w_1 + \alpha w_2\)
  - \(w_1\), \(w_2\): Gewichte der beiden Modelle
  - \(\alpha \in [0,1]\): Interpolationskoeffizient (0 für \(w_1\), 1 für \(w_2\), Werte dazwischen für die lineare Kombination der beiden Gewichte)
  - \(L(w(\alpha))\): Verlustwert bei den interpolierten Gewichten \(w(\alpha)\)

Code

import torch
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import linear_interpolation, visualize_linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model

# Linear Interpolation

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# model1, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# model2, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")
model1, _ = load_model(model_file="SimpleNetwork-ReLU-epoch1.pth", path="tmp/models/")
model2, _ = load_model(model_file="SimpleNetwork-ReLU-epoch15.pth", path="tmp/models/")


model1 = model1.to(device)
model2 = model2.to(device)
# Linear interpolation

# Test with a small dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)

alphas, losses,  accuracies = linear_interpolation(model1, model2, data_loader, loss_func, device)

_ = visualize_linear_interpolation(alphas, losses, accuracies,  "ReLU(1)-ReLU(15)",  size=(6, 4))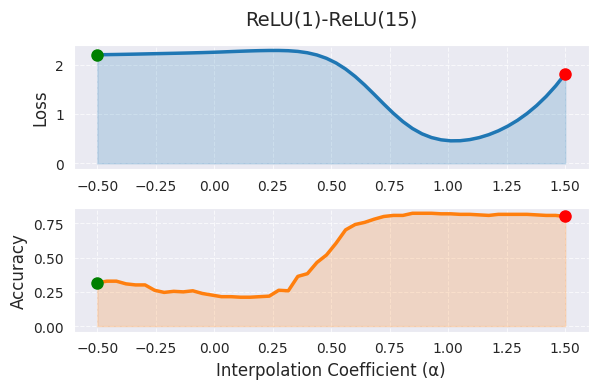

In der linearen Interpolation bedeutet α=0 das erste Modell (1 Epoche Training), α=1 das zweite Modell (15 Epochen Training), und die Werte dazwischen stellen Linearkombinationen der Gewichte beider Modelle dar. In dem Diagramm zeigt sich, dass die Verlustfunktionswerte mit steigendem α tendenziell abnehmen, was darauf hindeutet, dass das Modell während des Trainings in eine bessere Optimalstelle übergeht. Allerdings hat die lineare Interpolation die Beschränkung, dass sie nur ein sehr begrenztes Profil des hochdimensionalen Gewichtsraums zeigt. Der tatsächliche optimale Pfad zwischen den beiden Modellen ist höchstwahrscheinlich nichtlinear und die Erweiterung des α-Bereiches außerhalb von [0,1] erschwert die Interpretation.

Die Exploration von nichtlinearen Pfaden mit Bezier-Kurven oder Splines sowie die Visualisierung hochdimensionaler Strukturen durch PCA oder t-SNE können umfassendere Informationen liefern. In der Praxis wird die lineare Interpolation als Anfangsanalyseinstrumentarium verwendet und es ist ratsam, α auf den Bereich [0,1] oder leicht darüber hinaus zu beschränken. Eine umfassende Analyse in Verbindung mit anderen Visualisierungstechniken ist erforderlich, insbesondere wenn die Leistungsunterschiede zwischen den Modellen groß sind.

Im Folgenden finden Sie die PCA- und t-SNE-Analysen.

Code

import torch
from dldna.chapter_05.visualization.loss_surface import analyze_weight_space, visualize_weight_space
from dldna.chapter_04.utils.metrics import load_model, load_models_by_pattern


models, labels = load_models_by_pattern(
    activation_types=['ReLU'],
    # activation_types=['Tanh'],
    # activation_types=['GELU'],
    epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
)

# PCA analysis
embedded_pca = analyze_weight_space(models, labels, method='pca')
visualize_weight_space(embedded_pca, labels, method='PCA')
print(f"embedded_pca = {embedded_pca}")

# t-SNE analysis
embedded_tsne = analyze_weight_space(models, labels, method='tsne', perplexity=1)
visualize_weight_space(embedded_tsne, labels, method='t-SNE')
print(f"embedded_tsne = {embedded_tsne}") # Corrected: Print embedded_tsne, not embedded_pca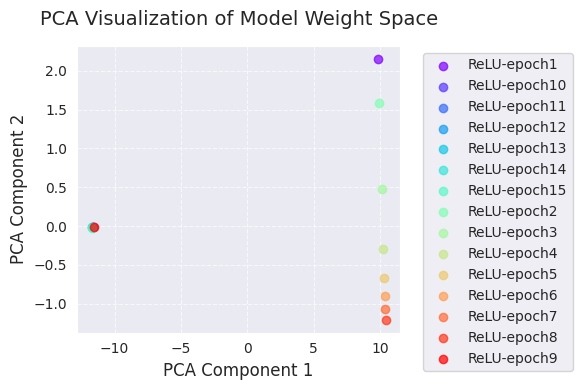

embedded_pca = [[ 9.8299894e+00  2.1538167e+00]
 [-1.1609798e+01 -9.0169059e-03]
 [-1.1640446e+01 -1.2218434e-02]
 [-1.1667191e+01 -1.3469303e-02]
 [-1.1691980e+01 -1.5136327e-02]
 [-1.1714937e+01 -1.6765745e-02]
 [-1.1735878e+01 -1.8110925e-02]
 [ 9.9324265e+00  1.5862983e+00]
 [ 1.0126298e+01  4.7935897e-01]
 [ 1.0256655e+01 -2.8844318e-01]
 [ 1.0319887e+01 -6.6510278e-01]
 [ 1.0359785e+01 -8.9812231e-01]
 [ 1.0392080e+01 -1.0731999e+00]
 [ 1.0418671e+01 -1.2047548e+00]
 [-1.1575559e+01 -5.1336871e-03]]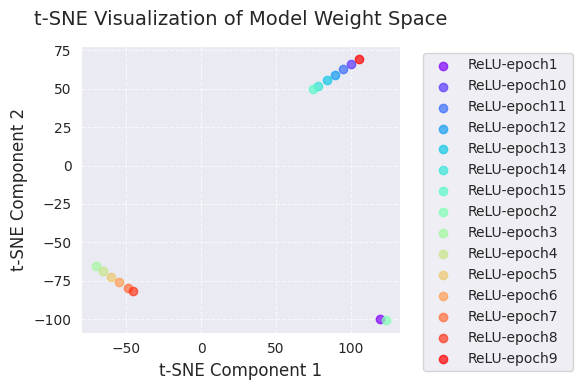

embedded_tsne = [[ 119.4719    -99.78837 ]
 [ 100.26558    66.285835]
 [  94.79294    62.795162]
 [  89.221085   59.253677]
 [  83.667984   55.70297 ]
 [  77.897224   52.022995]
 [  74.5897     49.913578]
 [ 123.20351  -100.34615 ]
 [ -70.45423   -65.66194 ]
 [ -65.55417   -68.90429 ]
 [ -60.166885  -72.466805]
 [ -54.70004   -76.077   ]
 [ -49.00131   -79.833694]
 [ -45.727974  -81.99213 ]
 [ 105.22419    69.45333 ]]

PCA- und t-SNE-Visualisierungen zeigen die Veränderungen im Modellgewichtungsraum während des Lernprozesses, projiziert in niedrige Dimensionen (2D).

PCA-Visualisierung:
- Die Punkte repräsentieren die Modellgewichte für jede Epoche. (Lila (Epoche 1) -> Rot (Epoche 9) -> Grüntöne (nach Epoche 10))
- Die Gewichte, die zu Beginn weit verstreut sind, sammeln sich im Laufe des Lernprozesses in bestimmten Bereichen.
- Insbesondere wird eine große Veränderung beim Übergang von Epoche 9 zu Epoche 10 beobachtet.
- PCA zeigt die Richtungen (Hauptkomponenten), in denen im Gewichtungsraum die größten Veränderungen auftreten.
t-SNE-Visualisierung:
- Ähnlich wie bei der PCA ändern sich die Farben der Punkte mit den Epochen und zeigen so die Veränderungen in der Gewichtsverteilung zu Beginn, Mitte und Ende des Lernprozesses.
- t-SNE ist eine nichtlineare Dimensionsreduktionsmethode, die auf der Erhaltung von lokalen Nachbarschaftsbeziehungen in hochdimensionalen Räumen basiert.
- Die Gruppen Epoche 1-9 und Epoche 10-15 sind relativ klar getrennt, was das PCA-Ergebnis bestätigt.

Durch diese Visualisierungen kann man eine intuitive Vorstellung von den Veränderungen der Modellgewichte während des Lernprozesses und von der Gewichtsraumsuche durch den Optimierungsalgorithmus erhalten. Insbesondere ermöglichen die gemeinsame Nutzung von PCA und t-SNE, globale Veränderungen (PCA) und lokale Strukturen (t-SNE) gleichzeitig zu erfassen.

Höhenlinienkarte (Contour Plot)

Eine Höhenlinienkarte zeichnet Linien, die Punkte gleicher Werte der Verlustfunktion in einer 2D-Ebene verbinden, um das Profil der Verlustfläche zu visualisieren. Ähnlich wie die Höhenlinien auf einem Topografischen Karten, zeigt sie die “Höhen” der Verlustfunktion an.

Das allgemeine Vorgehen ist folgendes:

Referenzpunkt festlegen: Wähle einen Referenzparameter des Modells (\(w_0\)). (z.B. die Parameter eines trainierten Modells)
Richtungsvektoren wählen: Wähle 2 Richtungsvektoren (\(d_1\), \(d_2\)). Diese Vektoren bilden eine Basis der 2D-Ebene.
- Typische Wahl: Zufällige (random) Richtungen, Hauptidealrichtungen aus PCA (Prinzipalkomponentenanalyse), oder die ersten 2 Eigenvektoren des Hessian-Matrix mit den größten Eigenwerten, z.B. durch PyHessian. Im letzteren Fall repräsentieren sie die Richtungen, in denen sich der Wert der Verlustfunktion am stärksten ändert.
Parameterstörung: Störe (perturb) die Parameter entlang der beiden gewählten Richtungsvektoren \(d_1\), \(d_2\) um den Referenzpunkt \(w_0\).

\(w(\lambda_1, \lambda_2) = w_0 + \lambda_1 d_1 + \lambda_2 d_2\)
- \(\lambda_1\), \(\lambda_2\): Skalare Faktoren für jeden Richtungsvektor (z.B. Werte in einem Bereich von -0.2 bis 0.2, gleichmäßig verteilt)
Verlustwerte berechnen: Berechne den Wert der Verlustfunktion für jedes \((\lambda_1, \lambda_2)\)-Kombination, indem du die gestörten Parameter \(w(\lambda_1, \lambda_2)\) in das Modell einsetzt.
Höhenlinienplot: Zeichne eine 2D-Höhenlinienkarte mit den Daten \((\lambda_1, \lambda_2, L(w(\lambda_1, \lambda_2)))\). (z.B. mit contour oder tricontourf von matplotlib)

Höhenlinienkarten visualisieren die lokale Geometrie der Verlustfläche und können zusammen mit der Darstellung des Optimierungspfad (trajectory) verwendet werden, um das Verhalten des Optimierungsverfahrens zu analysieren.

Code

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.optimizers.basic import SGD, Adam

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)


# pyhessian
data = []  # List to store the calculated result sets
top_n = 4  # Must be an even number.  Each pair of eigenvectors is used.  2 is the minimum.  10 means 5 graphs.
top_eigenvalues, top_eignevectors = hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True)

# Define the scale with lambda.
lambda1, lambda2 = np.linspace(-0.2, 0.2, 40).astype(np.float32), np.linspace(-0.2, 0.2, 40).astype(np.float32)

# If top_n=10, a total of 5 pairs of graphs can be drawn.
for i in range(top_n // 2):
    x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eignevectors[i*2:(i+1)*2], data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device)
    data.append((x, y, z))

_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=True)
_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=False) # Changed "ReLu" to "ReLU" for consistency

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/autograd/graph.py:825: UserWarning: Using backward() with create_graph=True will create a reference cycle between the parameter and its gradient which can cause a memory leak. We recommend using autograd.grad when creating the graph to avoid this. If you have to use this function, make sure to reset the .grad fields of your parameters to None after use to break the cycle and avoid the leak. (Triggered internally at ../torch/csrc/autograd/engine.cpp:1201.)
  return Variable._execution_engine.run_backward(  # Calls into the C++ engine to run the backward pass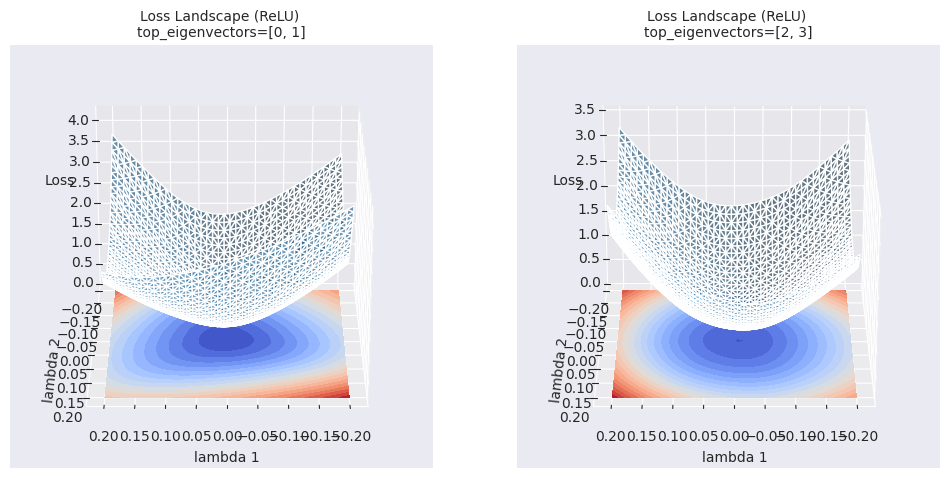

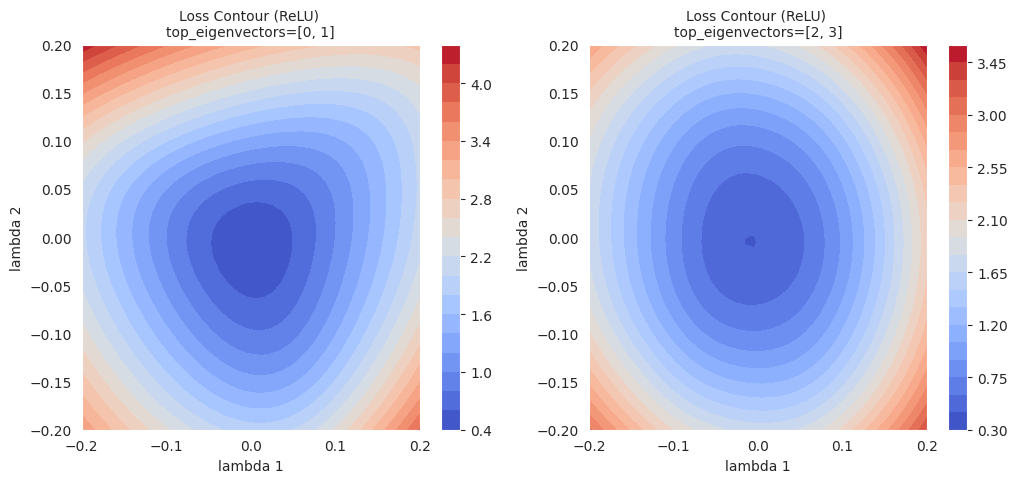
Höhenlinienkarte bietet reichere Informationen für lokale Bereiche im Vergleich zu einfachen linearen Interpolationen. Während lineare Interpolation die Änderung des Verlustfunktionswerts entlang eines eindimensionalen Pfades zwischen zwei Modellen zeigt, visualisiert eine Höhenlinienkarte die Änderungen der Verlustfunktion in einer zweidimensionalen Ebene, wobei die beiden gewählten Richtungen (\(\lambda_1\), \(\lambda_2\)) als Achsen dienen. Auf diese Weise können subtile Veränderungen entlang des Optimierungspfades, lokale Minima, Sattelpunkte und Barrieren dazwischen sichtbar gemacht werden, die mit linearen Interpolationen nicht erkannt werden könnten.

5.3.2 Tiefe Techniken zur Analyse der Verlustlandschaft

Über einfache Visualisierungen (lineare Interpolation, Konturkarten) hinaus werden fortgeschrittene Analysetechniken erforscht, um die Verlustlandschaft von Deep-Learning-Modellen tiefer zu verstehen.

Topologische Datenanalyse (Topological Data Analysis, TDA):
- Kernidee: Verwendung von topologischen Werkzeugen zur Analyse der “Form” der Verlustlandschaft, insbesondere ihrer Zusammenhangskomponenten.
- Hauptmethoden: Persistente Homologie (persistent homology), Mapper-Algorithmus u. a.
- Anwendung: Durch die Analyse der Komplexität der Verlustlandschaft, der Verbindungsstruktur lokaler Minima, der Eigenschaften von Sattelpunkten usw., können Einblicke in Lern-Dynamiken und Generalisierungsfähigkeit gewonnen werden. (siehe “Tiefgang: Topologische Analyse der Verlustlandschaft” für Details)
Mehrskalenanalyse (Multi-scale Analysis):
- Kernidee: Die Verlustlandschaft wird auf verschiedenen Skalen analysiert, um sowohl makroskopische als auch mikroskopische Strukturen zu erfassen.
- Hauptmethoden: Wavelet-Transformation, Skalierungstheorie (scale-space theory) u. a.
- Anwendung: Durch die Analyse der Rauheit und der skalenabhängigen Verteilung von Merkmalen in der Verlustlandschaft können das Verhalten von Optimierungsverfahren und die Schwierigkeiten des Lernprozesses besser verstanden werden. (siehe “Tiefgang: Mehrskalenanalyse der Verlustlandschaft” für Details)

Diese fortgeschrittenen Analysetechniken liefern abstraktere und quantitativere Informationen über die Verlustlandschaft, die dazu beitragen können, den Lernprozess von Deep-Learning-Modellen tiefer zu verstehen und bessere Modellentwürfe sowie Optimierungsstrategien zu entwickeln.

Code

import torch
import torch.nn as nn  # Import the nn module
from torch.utils.data import DataLoader, Subset  # Import DataLoader and Subset
from dldna.chapter_05.visualization.loss_surface import  analyze_loss_surface_multiscale
from dldna.chapter_04.utils.data import get_dataset  # Import get_dataset
from dldna.chapter_04.utils.metrics import load_model  # Import load_model

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Load dataset and create a small subset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# Load model (example: SimpleNetwork-ReLU)
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
model = model.to(device)

_ = analyze_loss_surface_multiscale(model, data_loader, loss_func, device)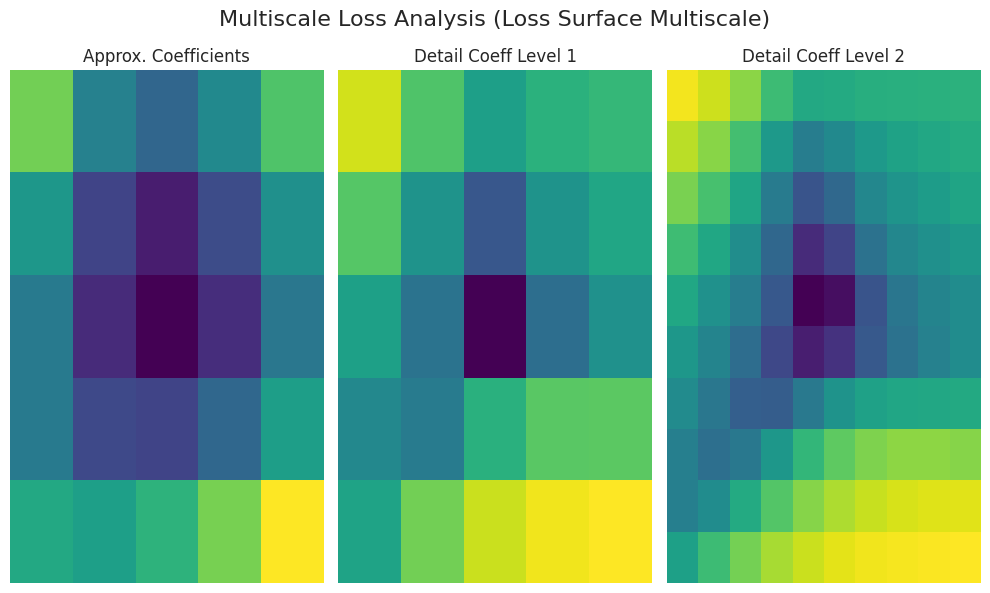

Die Funktion analyze_loss_surface_multiscale wurde verwendet, um die Verlustoberfläche des mit dem FashionMNIST-Datensatz trainierten Modells SimpleNetwork-ReLU aus mehreren Skalen zu analysieren und zu visualisieren.

Grafikinterpretation (basiert auf Wavelet-Transformation):

Approx. Coefficients (Approximationskoeffizienten): Stellen die allgemeine Form (globale Struktur) der Verlustoberfläche dar. Es ist wahrscheinlich, dass ein Minimum im Zentrum (niedriger Verlustwert) vorhanden ist.
Detail Coeff Level 1/2 (Detailkoeffizienten): Stellen kleinere Skalenveränderungen dar. “Level 1” zeigt mittlere Skalen, während “Level 2” die feinsten Skalen von Kanten, lokalen Minima, Sattelpunkten und Rauschen anzeigt.
Farben: Dunkle Farben (niedriger Verlust), helle Farben (hoher Verlust)
Die Ergebnisse können sich je nach Implementierung der Funktion analyze_loss_surface_multiscale (z. B. Wavelet-Funktion, Zerlegungsstufe) unterscheiden.
Diese Visualisierung zeigt nur einen Teil der Verlustoberfläche und es ist schwierig, die Komplexität eines hochdimensionalen Raums vollständig zu erfassen.

Die Multiskalenanalyse zerlegt die Verlustoberfläche in verschiedene Skalen, um multischichtige Strukturen zu zeigen, die durch einfache Visualisierung schwer zu erkennen sind. Auf großen Skalen können allgemeine Trends erkannt werden, während auf kleinen Skalen lokale Änderungen sichtbar sind, was zur Verbesserung des Verständnisses von Optimierungsverfahren, Lernschwierigkeiten und Generalisierungsfähigkeit beiträgt.

Klicken Sie hier, um den Inhalt anzuzeigen (Topologiebasierte Analyse der Verlustfläche)

Topologie-basierte Analyse von Verlustflächen

Topologie ist das Gebiet, das geometrische Eigenschaften untersucht, die bei stetigen Deformationen invariant bleiben. In der Tiefenlernung wird topologische Analyse zur Untersuchung topologischer Merkmale wie Zusammenhang (connectivity), Löcher (holes) und Hohlräume (voids) von Verlustflächen verwendet, um Einblicke in die Lernmechanik und Generalisierungseigenschaften zu gewinnen.

Kernkonzepte:

Sublevel-Menge: Für eine gegebene Funktion \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) und einen Schwellwert \(c\) ist die Menge definiert als \(f^{-1}((-\infty, c]) = {x \in \mathbb{R}^n | f(x) \leq c}\). In der Verlustfunktion repräsentiert sie den Bereich des Parameterraums, in dem der Verlust einen bestimmten Wert nicht überschreitet.
Persistente Homologie: Beim Nachverfolgen der Änderungen von Sublevel-Mengen werden die Entstehung und Auflösung topologischer Merkmale (0-dimensionale: zusammenhängende Komponenten, 1-dimensionale: Schleifen, 2-dimensionale: Hohlräume, …) aufgezeichnet.
- 0-dimensionales Merkmal (Zusammenhängende Komponenten): Anzahl der verbundenen Bereiche. In Verlustflächen ist sie mit der Anzahl von lokalen Minima in Beziehung.
- 1-dimensionales Merkmal (Schleifen): Anzahl von geschlossenen Schleifen. In Verlustflächen steht es für die Existenz von Pfaden, die Sattelpunkte umgeben.
Persistenzdiagramm: Es stellt die Entstehungs- (birth) und Auflösungspunkte (death) der topologischen Merkmale als Punkte in einer Koordinatenebene dar. Die \(y\)-Koordinate eines Punktes (\(\text{death} - \text{birth}\)) repräsentiert die “Lebensdauer” oder “Persistenz” des Merkmals, wobei ein größerer Wert für eine stabilere Eigenschaft steht.
Flaschenhals-Distanz: Es ist eine Methode zur Messung der Distanz zwischen zwei Persistenzdiagrammen. Durch das Finden einer optimalen Zuordnung (optimal matching) von Punkten in beiden Diagrammen wird die maximale Distanz zwischen den zugeordneten Punkten berechnet.

Mathematische Hintergründe (kurz):

Simplizialer Komplex: Ein Konzept, das Punkte (Vertices), Linien (Edges), Dreiecke (Triangles) und Tetraeder (Tetrahedra) verallgemeinert, um topologische Räume zu approximieren.
Randoperator: Ein Operator, der den Rand eines simplizialen Komplexes berechnet.
Homologiegruppe: Eine Gruppe (group), die durch den Randoperator definiert wird und “Löcher” in einem topologischen Raum repräsentiert.
Persistenzhomologie-Algorithmus: Durch die Filtrierung von Sublevel-Mengen wird ein simplizialer Komplex konstruiert, und die Veränderungen der Homologiegruppen werden nachverfolgt, um das Persistenzdiagramm zu berechnen. (Für weitere Details siehe Referenz [1])

Anwendung in der Tiefenlernungsforschung: * Strukturanalyse der Verlustoberfläche: Durch das Persistence-Diagramm kann die Komplexität der Verlustoberfläche, die Anzahl und Stabilität lokaler Minima sowie die Existenz von Sattelpunkten ermittelt werden. * Beispiel: Gur-Ari et al., 2018 zeigten, dass breite (wide) Netzwerke eine einfachere topologische Struktur aufweisen als schmale (narrow) Netzwerke. * Vorhersage der Generalisierungsfähigkeit: Merkmale des Persistence-Diagramms (z. B. das Lebensdauer des 0-dimensionalen Merkmals mit der längsten Lebensdauer) können mit der Generalisierungsfähigkeit des Modells korreliert sein. * Beispiel: Perez et al., 2022 schlugen eine Methode zur Vorhersage der Generalisierungsfähigkeit des Modells mithilfe von Merkmalen des Persistence-Diagramms vor. * Mode Connectivity: Es werden Pfade gefunden, die verschiedene lokale Minima verbinden, und die Energiebarrieren (energy barriers) entlang dieser Pfade analysiert. * Beispiel: Garipov et al., 2018

Referenzen:

Edelsbrunner, H., & Harer, J. (2010). Computational Topology: An Introduction. American Mathematical Society.
Gur-Ari, G., Roberts, D. A., & Dyer, E. (2018). Gradient descent happens in a tiny subspace. arXiv preprint arXiv:1812.04754.
Perez, D., Masoomi, A., DiCecco, J., & Chwialkowski, K. (2022). Relating loss landscape topology to generalization with persistent homology. In International Conference on Machine Learning (pp. 17953-17977). PMLR.
Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D. P., & Wilson, A. G. (2018). Loss surfaces, mode connectivity, and fast ensembling of dnns. Advances in neural information processing systems, 31.

Klicken Sie hier, um den Inhalt anzuzeigen (Deep Dive: Analyse der Mehrskalen-Verlustoberfläche)

Mehrskalige Analyse der Verlustoberfläche

Die Verlustoberfläche von Deep-Learning-Modellen weist Merkmale verschiedener Skalen auf. Von großen Tälern (valleys) und Graten (ridges) bis hin zu kleinen Unebenheiten (bumps) und Löchern (holes), beeinflussen geometrische Strukturen unterschiedlicher Größe den Lernprozess. Die mehrskalige Analyse ist eine Methode, die diese Merkmale verschiedener Skalen trennt und analysiert.

Kernidee:

Wavelet-Transformation (WT): Die Wavelet-Transformation ist ein mathematisches Werkzeug, das ein Signal in verschiedene Frequenzkomponenten zerlegt. Wenn man sie auf die Verlustfunktion anwendet, kann man Merkmale verschiedener Skalen trennen.
- Kontinuierliche Wavelet-Transformation (Continuous Wavelet Transform, CWT):
  
  \(W(a, b) = \int\_{-\infty}^{\infty} f(x) \psi\_{a,b}(x) dx\)
  - \(f(x)\): die zu analysierende Funktion (Verlustfunktion)
  - \(\psi\_{a,b}(x) = \frac{1}{\sqrt{a}}\psi(\frac{x-b}{a})\): Wavelet-Funktion (mother wavelet \(\psi\) skaliert (\(a\)) und verschoben (\(b\)))
  - \(W(a, b)\): Wavelet-Koeffizient an der Skala \(a\) und Position \(b\)
- Mother Wavelet: eine Funktion, die bestimmte Bedingungen erfüllt (z.B. Mexican hat wavelet, Morlet wavelet) (siehe Referenz [2] für Details)
Mehrskalenanalyse (Multi-resolution Analysis, MRA): Die Diskretisierung der CWT, um ein Signal in verschiedene Auflösungslevel zu zerlegen.

Mathematischer Hintergrund (kurz):

Skalierungsfunktion: eine Funktion, die die Niederfrequenzkomponenten darstellt.
Wavelet-Funktion: eine Funktion, die die Hochfrequenzkomponenten darstellt.
Zerlegung: ein Signal wird in Kombinationen aus Skalierungsfunktion und Wavelet-Funktion zerlegt.
Rekonstruktion: das zerlegte Signal wird wieder in das ursprüngliche Signal zurücktransformiert. (siehe Referenz [1] für Details)

Anwendung in Deep-Learning-Forschung:

Analyse der Verlustoberflächenrauhigkeit: Die Wavelet-Transformation kann verwendet werden, um die Rauheit (roughness) der Verlustoberfläche zu quantifizieren und ihren Einfluss auf die Lernrate und die Generalisierungslistung zu analysieren.
- Beispiel: Li et al., 2019 haben]([https://www.google.com/search?q=https://www.google.com/search%3Fq%3Dhttps://arxiv.org/abs/1910.00779)%20]) eine wavelet-basierte mehrskalige Analyse verwendet, um den Einfluss der Rauheit der Verlustoberfläche auf die Lernkinetik zu untersuchen.
Analyse von Optimierungsalgorithmen: Durch die Analyse des Fortschreitens von Optimierungsalgorithmen auf verschiedenen Skalen kann man das Verhalten dieser Algorithmen besser verstehen.

Referenzen: 1. Mallat, S. (2008). Eine Wellenlettour durch die Signalverarbeitung: der spärliche Weg. Academic press. 2. Daubechies, I. (1992). Zehn Vorträge über Wavelets. Society for industrial and applied mathematics. 3. Li, Y., Hu, W., Zhang, Y., & Gu, Q. (2019). Mehrskalenganalyse der Verlustlandschaft von tiefen Netzen. arXiv preprint arXiv:1910.00779.

5.4 Visualisierung des Optimierungsprozesses: Einblick in die Tiefenlernen-Trainingsgeheimnisse mit der Gaußfunktion

Die tatsächliche Verlustfläche (loss surface) eines Tiefenlernmodells existiert in einem ultradimensionalen Raum mit Millionen bis Milliarden von Dimensionen und weist eine sehr komplexe geometrische Struktur auf. Daher ist es praktisch unmöglich, sie direkt zu visualisieren und zu analysieren. Darüber hinaus sind die tatsächliche Verlustfläche anfällig für verschiedene Probleme wie nicht differenzierbare Punkte, Unstetigkeiten und numerische Instabilitäten, was eine theoretische Analyse erschwert.

5.4.1 Approximative Analyse mit der Gaußfunktion: Einblick in die Einfachheit

Um diese Grenzen zu überwinden und den Optimierungsprozess konzeptuell zu verstehen, verwenden wir die Gaußfunktion (Gaussian function), die glatt (smooth), kontinuierlich (continuous) und konvex ist, um die Verlustfläche zu approximieren.

Gründe für die Verwendung der Gaußfunktion (Vorteile der Approximation der Verlustfläche):

Differenzierbarkeit: Die Gaußfunktion ist an jedem Punkt unendlich oft differenzierbar (infinitely differentiable). Dies ist eine wesentliche Bedingung für die Anwendung und Analyse von Optimierungsalgorithmen basierend auf Gradientenabstieg (gradient descent).
Konvexität (Convexity): Ein einzelner Gaußscher Verteilungsfunktion ist eine konvexe Funktion (convex function). Konvexe Funktionen haben nur ein globales Minimum, wodurch die Analyse der Konvergenz von Optimierungsalgorithmen vereinfacht wird.
Symmetrie: Die Gaußfunktion hat eine symmetrische Form um den Mittelpunkt. Dies bedeutet, dass es keine Verzerrungen (bias) in bestimmten Richtungen der Verlustfläche gibt und ermöglicht es, vereinfachende Annahmen bei der Analyse des Algorithmusverhaltens zu machen.
Mathematische Einfachheit: Die Gaußfunktion kann durch eine vergleichsweise einfache Formel dargestellt werden, was die mathematische Analyse erleichtert. Dies ermöglicht es, das Funktionsprinzip von Optimierungsalgorithmen theoretisch zu verstehen und vorhersagbare Ergebnisse abzuleiten.
Verstellbare Komplexität: Die Komplexität kann durch die Verwendung eines Gauß-Mischungsmodells (Gaussian Mixture Model, GMM) angepasst werden.

Formel der Gaußfunktion:

\(z = A \exp\left(-\left(\frac{(x-x_0)^2}{2\sigma_1^2} + \frac{(y-y_0)^2}{2\sigma_2^2}\right)\right)\)

\(A\): Amplitude (Amplitude) - maximale Höhe der Verlustfunktion
\(x_0\), \(y_0\): Zentrum (Center) - Position des Minimums der Verlustfunktion
\(\sigma_1\), \(\sigma_2\): Standardabweichungen in x- und y-Richtung (Standard Deviations) - Form der Gaußfunktion

Die tatsächliche Verlustfläche kann viel komplexer als eine Gaußfunktion sein (z.B. mehrere lokale Minima, Sattelpunkte, Plateaus). Jedoch bietet die Approximation mit einer einzelnen Gaußfunktion einen nützlichen Ausgangspunkt, um grundlegende Eigenschaften des Optimierungsverhaltens (z.B. Konvergenzgeschwindigkeit, Schwingmuster) zu verstehen und verschiedene Algorithmen miteinander zu vergleichen. Für die Simulation komplexerer Verlustflächen können mehrere Gaußfunktionen in einem Gauß-Mischungsmodell (Gaussian Mixture Model, GMM) kombiniert werden.

In diesem Kapitel approximieren wir die Verlustfläche mit einer einzelnen Gaußfunktion und wenden verschiedene Optimierungsalgorithmen (SGD, Adam usw.) an, um die Lerntrajektorien zu visualisieren. Dadurch werden wir die dynamischen Eigenschaften und Vor- und Nachteile der Algorithmen intuitiv verstehen.

Code

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset  
from dldna.chapter_04.utils.metrics import load_model  
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.visualization.gaussian_loss_surface import (
    get_opt_params,  visualize_gaussian_fit, train_loss_surface, visualize_optimization_path
)


# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)

# Loss surface data generation
top_n = 2
top_eigenvalues, top_eignevectors = hessian_eigenvectors(
    model=trained_model,
    loss_func=loss_func,
    data_loader=data_loader,
    top_n=top_n,
    is_cuda=True
)

# Define lambda range
d_min, d_max, d_num = -1, 1, 30
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)

# Calculate loss surface
x, y, z = xy_perturb_loss(
    model=trained_model,
    top_eigenvectors=top_eignevectors,
    data_loader=data_loader,
    loss_func=loss_func,
    lambda1=lambda1,
    lambda2=lambda2,
    device=device
)


# After generating loss surface data
popt, _, offset = get_opt_params(x, y, z)

# Visualize Gaussian fitting
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num)

# View from a different angle
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num,
                      elev=30, azim=45)

Function parameters = [29.27164346 -0.0488573  -0.06687705  0.7469189   0.94904458]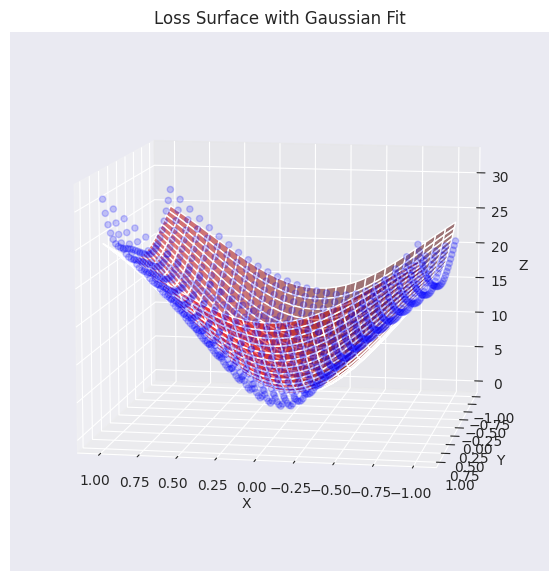

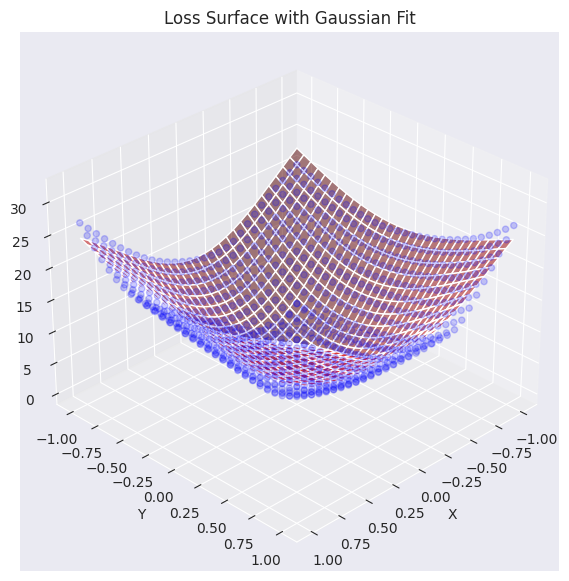
Die tatsächlichen Verlustflächendaten (blaue Punkte) wurden mit einer durch eine Gauß-Funktion approximierten Fläche (rot) überlagert visualisiert. Wie aus dem Graphen ersichtlich ist, erfasst die generierte Gauß-Funktion die allgemeine Tendenz der ursprünglichen Verlustflächendaten (insbesondere die konkave Form im Zentrum) ziemlich gut und erstellt eine ähnliche Fläche. Nun werden wir diese approximierte Verlustflächenfunktion verwenden, um den Pfad zu analysieren und zu visualisieren, wie verschiedene Optimierungsalgorithmen (Optimizer) das Minimum finden.

5.4.2 Pfadvisualisierung

Mit einer durch eine Gauß-Funktion angenäherten Verlustfläche werden wir visualisieren, wie der Optimierer in einer 2D-Ebene arbeitet.

Deutsch-Text	Übersetzungsanweisungen
Dieses Beispiel zeigt, wie man eine Tabelle beibehält, während man Koreanisch in Deutsch übersetzt.	Elemente, die nicht übersetzt werden dürfen: LaTeX-Math-Ausdrücke, Tabellen-Markdown-Syntax, Formatierungselemente innerhalb der Tabelle
\(a + b = c\)	Diese Gleichung wird nicht konvertiert.
Text zur Übersetzung: Dieser Satz wurde auf Koreanisch verfasst.	Übersetzter Text: Dieser Satz wurde auf Koreanisch verfasst.

Code

# Gaussian fitting
popt, _, offset = get_opt_params(x, y, z)
gaussian_params = (*popt, offset)

# Calculate optimization paths
points_sgd = train_loss_surface(
    lambda params: SGD(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)
points_sgd_m = train_loss_surface(
    lambda params: SGD(params, lr=0.05, momentum=0.8),
    [d_min, d_max], 100, gaussian_params
)
points_adam = train_loss_surface(
    lambda params: Adam(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)

# Visualization
visualize_optimization_path(
    x, y, z, popt, offset,
    [points_sgd, points_sgd_m, points_adam],
    act_name="ReLU"
)

Das Diagramm zeigt die Lernpfade von drei Optimierungsalgorithmen (SGD, Momentum SGD, Adam) auf einer durch eine Gauß-Funktion approximierten Verlustfläche. In flachen und steilen Bereichen zeigen die drei Algorithmen jeweils unterschiedliche Eigenschaften.

SGD (orangefarben): In flachen Bereichen nähert er sich dem Minimum mit relativ breiten Schwingungen, aber in steilen Bereichen schwingt er mit noch größeren Amplituden und zeigt eine verlangsamt Konvergenzgeschwindigkeit in der Nähe des Minimums.
Momentum SGD (grün): Er nähert sich dem Minimum mit weniger Schwingungen und einem glatteren Kurvenverlauf. Dank des Trägheitseffekts (momentum) findet er das Minimum relativ stabil, auch in steilen Bereichen.
Adam (rot): Mit den geringsten Schwingungen reagiert Adam sensibel auf Veränderungen der Steigung und folgt einem effizienten Pfad zum Minimum. Besonders in steilen Bereichen zeigt er eine relativ schnelle Konvergenzgeschwindigkeit. Dies ist auf Adams adaptiven Lernrateinstellungsmechanismus zurückzuführen.

In der Praxis wird SGD mit Momentum viel bevorzugt gegenüber reinem SGD, und adaptive Optimierungsalgorithmen wie Adam oder AdamW werden ebenfalls weit verbreitet eingesetzt. Allgemein gilt, dass die Verlustfläche in den meisten Bereichen flach ist, aber in der Nähe des Minimums oft eine schmale, tiefe Schlucht bildet. Dies führt dazu, dass hohe Lernraten das Über- oder Divergieren von Minima gefährden; daher wird typischerweise ein Lernratenplaner (learning rate scheduler) verwendet, um die Lernrate allmählich zu verringern. Zudem ist es wichtig, neben der Wahl des Optimierungsalgorithmus auch geeignete Lernratenplaner, Batchgrößen und Regularisierungstechniken in Betracht zu ziehen.

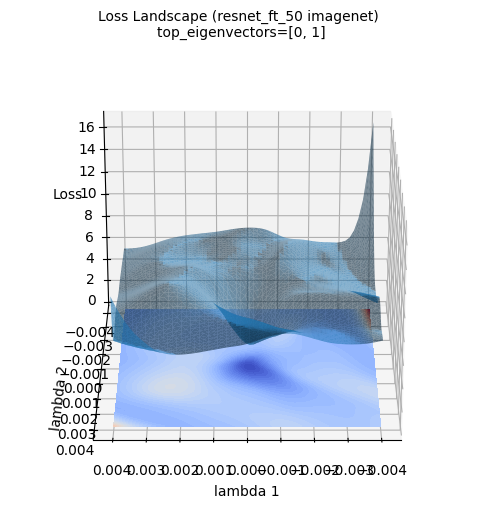
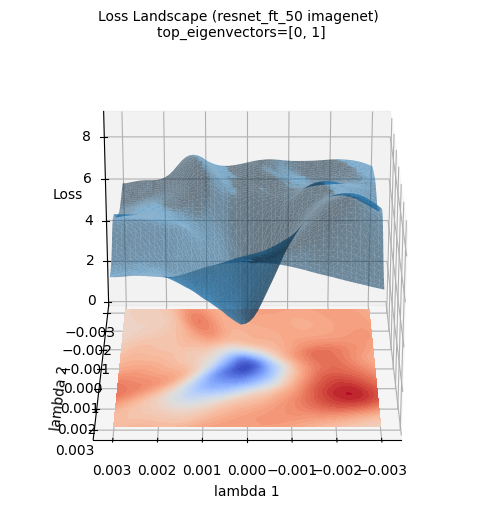
Die obigen Verlustflächenbilder visualisieren die 3D-Verlustfläche eines neu auf dem ImageNet-Datensatz trainierten ResNet-50-Modells. (Es wurden die beiden führenden Eigenvektoren der Hesse-Matrix, die mit PyHessian berechnet wurde, als Achsen verwendet). Im Gegensatz zur Approximation durch eine Gauß-Funktion zeigt die tatsächliche Verlustfläche von tiefen neuronalen Netzen eine viel komplexere und unregelmäßige Struktur. Dennoch bleibt der allgemeine Trend bestehen, dass das Minimum in der Mitte (blauer Bereich) liegt. Solche Visualisierungen helfen, ein intuitives Verständnis dafür zu entwickeln, wie komplex die topografischen Merkmale von tiefen neuronalen Netzwerken sind und warum Optimierung eine schwierige Aufgabe darstellt.

5.5 Dynamische Analyse des Optimierungsprozesses: Untersuchung der Lerntrajektorie

Das Verständnis der dynamischen Eigenschaften (Dynamics) darüber, wie Optimierungsalgorithmen welchen Pfad sie beim Auffinden des Minimums der Verlustfunktion im Deep-Learning-Modell lernen, ist wichtig. Insbesondere mit dem Auftreten von Large Language Models (LLMs), wurde die Analyse und Kontrolle der Lern-Dynamik von Modellen mit Milliarden von Parametern noch wichtiger.

5.5.1 Charakteristika des Trainingsprozesses

Der Trainingsprozess im Deep-Learning-Modell kann in Anfangs-, Mittel- und Endphase unterteilt werden, wobei jede Phase ihre eigenen Merkmale hat.

Phasencharakteristika der Lernung:
- Anfänglich: Der Gradientennorm (gradient norm) ist groß und stark schwankend, während der Verlustfunktionswert rapide abnimmt.
- Mittlerweile: Die Gradienten stabilisieren sich, während die Parameter die optimale Region (optimal region) erforschen (explore).
- Später: Die Parameter werden in der Nähe eines lokalen Optimums (local optimum) feinjustiert (fine-tuning). (Frühes Stoppen ist wichtig)
Gradienteigenschaften pro Schicht:
- In tiefen neuronalen Netzen neigen Gradienten dazu, größer zu sein, je näher sie der Eingangsschicht sind, und kleiner zu werden, je näher sie der Ausgabeschicht kommen (Vanishing Gradient Problem).
- Dies ist auf die Kette von Ableitungen beim Backpropagation zurückzuführen.
- Residuelle Verbindungen (residual connections) mildern diese Ungleichgewichte und fördern eine stabile Lernung in tieferen Schichten.
Parameterabhängigkeit:
- Neuronale Netzparameter sind voneinander abhängig, was den Optimierungsprozess nichtlinear macht.
- Einige Parameter können einen größeren Einfluss auf das Lernen haben, daher ist die Balance zwischen Parametern wichtig.
Analyse des Optimierungspfads:
- Der Pfad, den die Parameter auf der Verlustoberfläche während des Optimierungsprozesses zurücklegen, wird als Optimierungspfad (optimization path) bezeichnet.
- Regionale Minima in breiten und flachen Tälern (valleys) neigen dazu, bessere Generalisierungseigenschaften (generalization performance) zu haben als schmale und spitze Täler.
- In hochdimensionalen Räumen sind Sattelpunkte (saddle points) sehr häufig. (Momentum, Adam etc. sind so gestaltet, um diese zu vermeiden)
- In flachen Bereichen der Verlustoberfläche kann die Lernung aufgrund kleiner Gradienten langsamer werden. (Adaptive Lernratealgorithmen helfen hierbei)

5.5.2 Analyse und Kontrolle der Lernstabilität

Methoden zur Stabilitätsanalyse

Für die Analyse der Stabilität (stability) des Optimierungsprozesses können folgende Methoden verwendet werden:

Erkennung von Gradientenphänomenen:
- Erkennung von Phänomenen wie verschwindende oder explodierende Gradienten.
- Periodische Beobachtung der Gradientennorm (norm) während des Trainings.
Hesssche Matrixbasierte Analyse:
- Die Verteilung der Eigenwerte und die Konditionszahl (condition number) der Hessian-Matrix spiegeln die Stabilität des Optimierungspfads wider.
- (Siehe Hesssche Matrix-basierte Visualisierung in Abschnitt 5.3)
Echtzeit-Monitoring:
- Echtzeit-Überwachung von Gradientennorm, Parameteraktualisierungsgröße, Verlustfunktionswert und Leistungsindikatoren während des Lernens.

Stabilisierungstechniken (Stabilization Techniques)

Gradientenclipping (Gradient Clipping): Die Größe des Gradients (norm) wird so begrenzt, dass sie einen Schwellenwert (threshold) nicht überschreitet.

\(g \leftarrow \text{clip}(g) = \min(\max(g, -c), c)\)
\(g\): Gradient, \(c\): Schwellenwert
Anpassungsfähige Lernrate (Adaptive Learning Rate): Adam, RMSProp, Lion, Sophia passen die Lernrate automatisch anhand der Gradientstatistik an.
Lernratenplaner (Learning Rate Scheduler): Die Lernrate wird nach und nach reduziert basierend auf den Trainings-Epochen oder dem Validierungsverlust.
Hyperparameter-Optimierung (Hyperparameter Optimization): Automatische Suche/Anpassung von Hyperparametern, die für die Optimierung relevant sind.

Aktuelle Forschungstrends

Die aktuelle (2024) Forschung zur Lerndynamik entwickelt sich in folgende Richtungen:

Vorhersagbare Stabilisierung (Predictive Stabilization): Unstabilitätsfaktoren werden vor dem Training durch die Analyse der Modellstruktur, Initialisierung und Datensatzmerkmale vorausgehen/verringert.
Integrierte Analyse (Unified Analysis): Die Optimierungsalgorithmen werden tiefer verstanden, indem Krümmungsinformationen (Hessematrix) und Gradientstatistik gemeinsam analysiert.
Automatisierte Steuerung (Automated Control): Hyperparameter von Optimierungsalgorithmen werden durch Verstärkungslernen automatisch angepasst.

Diese Forschungen tragen dazu bei, das Deep-Learning-Modelltraining stabiler und effizienter zu gestalten und das “Black Box”-Verständnis zu verbessern.

Lassen Sie uns nun ein einfaches Beispiel betrachten, um die dynamische Analyse des Optimierungsprozesses zu erkunden.

Code

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Subset  # Import Subset
from dldna.chapter_05.visualization.train_dynamics import visualize_training_dynamics
from dldna.chapter_04.utils.data import get_dataset  
from dldna.chapter_04.utils.metrics import load_model  

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Load the FashionMNIST dataset (both training and testing)
train_dataset, test_dataset = get_dataset(dataset="FashionMNIST")
train_loader = DataLoader(train_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# Load a pre-trained model (e.g., ReLU-based network)
trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
trained_model = trained_model.to(device)

# Choose an optimizer (e.g., Adam)
optimizer = optim.Adam(trained_model.parameters(), lr=0.001)

# Call the training dynamics visualization function (e.g., train for 10 epochs with the entire training dataset)
metrics = visualize_training_dynamics(
    trained_model, optimizer, train_loader, loss_func, num_epochs=20, device=device
)

# Print the final results for each metric
print("Final Loss:", metrics["loss"][-1])
print("Final Grad Norm:", metrics["grad_norm"][-1])
print("Final Param Change:", metrics["param_change"][-1])
print("Final Weight Norm:", metrics["weight_norm"][-1])
print("Final Loss Improvement:", metrics["loss_improvement"][-1])

Das folgende Beispiel zeigt die verschiedenen Aspekte der erläuterten Lern-Dynamik (learning dynamics) in der Praxis. Mit einem vorab auf dem FashionMNIST-Datensatz trainierten SimpleNetwork-ReLU-Modell wurde weiteres Training unter Verwendung des Adam-Optimierungsalgorithmus durchgeführt und dabei wurden die folgenden fünf Kernmetriken (metrics) pro Epoche visualisiert.

Loss (Verlust): Zeigt, wie sich der Wert der Verlustfunktion während des Lernprozesses verringert. (blaue Linie)
Grad Norm (Gradienten-Norm): Stellt die Größe des Gradienten (L2-Norm) dar. (rote Linie)
Param Change (Parameter-Änderung): Zeigt die Änderung der Parameter (Gewichte) im Vergleich zur vorherigen Epoche (L2-Norm).
Weight Norm (Gewichtsnorm): Stellt die Größe aller Modellparameter (Gewichte) dar (L2-Norm). (lila Linie)
Loss Improvement (Verlustverbesserung): Zeigt, um wie viel sich der Wert der Verlustfunktion im Vergleich zur vorherigen Epoche verbessert hat. (gelbe Linie)

Die Grafik zeigt folgendes:

Loss: Der Verlustwert, der in der Anfangsepoche (Epoche 1) bei etwa 0.51 lag, nimmt während des Lernprozesses stetig ab und erreicht im letzten Durchlauf (Epoche 20) einen Wert von etwa 0.16.
Grad Norm: Die Gradienten-Norm, die in der Anfangsepoche bei etwa 4.5 lag, nimmt während des Lernprozesses allmählich ab und erreicht im letzten Durchlauf (Epoche 20) einen Wert von etwa 2.0.
Param Change: Die Parameter-Änderung ist am Beginn des Lernens groß, zeigt aber eine Tendenz zur Abnahme, während das Training fortschreitet. Dies bedeutet, dass die Änderungen der Parameter geringer werden, je näher das Modell dem Optimum kommt.
Weight Norm: Die Gewichtsnorm nimmt über den gesamten Lernprozess hinweg stetig zu. Dies bedeutet, dass die Parameter des Modells während des Trainings immer “größer” werden (obwohl dies nicht notwendigerweise Overfitting bedeutet).
Loss Improvement: Die Verlustverbesserung ist am Beginn des Lernens groß und zeigt eine Tendenz zur Abnahme, während das Training fortschreitet.

Durch dieses Beispiel kann man den Prozess, bei dem der Optimierungsalgorithmus die Verlustfunktion minimiert, visuell nachvollziehen sowie die Änderungen der Gradienten und Parameter beobachten. Dies ermöglicht eine intuitive Verständnis der Lern-Dynamik.

Zusammenfassung

In diesem Kapitel 5 haben wir verschiedene Themen im Zusammenhang mit der Optimierung bei tiefen neuronalen Netzen tiefer beleuchtet. Wir haben die Bedeutung von Gewichtsinitialisierungsmethoden, die Prinzipien und Eigenschaften verschiedener Optimierungsalgorithmen (SGD, Momentum, Adam, Lion, Sophia, AdaFactor) sowie die Visualisierung der Verlustoberfläche und die Analyse der Lern-Dynamik untersucht, um den Lernprozess von tiefen neuronalen Netzen besser zu verstehen.

In Kapitel 6 werden wir uns detailliert mit den Kernmethoden zur Verbesserung der Generalisierungsleistung von tiefen neuronalen Netzen befassen, insbesondere mit Regularisierungstechniken (L1/L2-Regularisierung, Dropout, Batch-Normalisierung, Daten-Augmentierung). Wir werden die Prinzipien und Effekte verschiedener Regularisierungsmethoden untersuchen und durch praktische Beispiele lernen, wie sie angewendet werden.

Übungsprobleme

Grundlegende Aufgaben

Manuelles Berechnen von SGD: Berechne die SGD-Update-Regeln für die folgende Verlustfunktion \(L(w) = w^2\) manuell in mehr als drei Schritten, wenn die Lernrate 0.1 und der Impuls 0.9 ist. Der Anfangsgewichtswert sei \(w_0 = 2\).
Vergleich der Konvergenzgeschwindigkeit des Gradientenabstiegs: Wende den Gradientenabstieg auf die einfache zweidimensionale Funktion \(f(x, y) = x^2 + 2y^2\) an und vergleiche die Konvergenzgeschwindigkeit für Lernraten von 0.1, 0.01 und 0.001.
Vergleich der Initialisierungsmethoden: Vergleiche Kaiming-Initialisierung und Xavier-Initialisierung und erkläre, warum Kaiming-Initialisierung bei Verwendung mit der ReLU-Aktivierungsfunktion besser geeignet ist.

Anwendungsprobleme

Adam-Optimierer: Erkläre das Funktionsprinzip des Adam-Optimierers (einschließlich Formeln) und beschreibe die Rolle der Parameter \(\beta_1\) und \(\beta_2\).
Batch-Normalisierung und Initialisierung: Erkläre, wie Batch-Normalisierung (Batch Normalization) die Bedeutung von Initialisierungsmethoden verringert und begründe dies.
Gaußsche Verlustebene: Beschreibe den Einfluss der Parameter einer Gaußfunktion (Amplitude, Zentrumspunkt, Varianz) auf das Optimierungsverfahren am Beispiel der Approximation einer Verlustfläche mit einer Gaußfunktion (Kapitel 5.5.1). Beobachte, wie sich die Optimierungspfade ändern, wenn die einzelnen Parameter variiert werden.

Vertiefende Aufgaben

Analyse des Lion-Optimierers: Erkläre die Kernidee des Lion-Optimierers (einschließlich Formeln) und analysiere seine Vor- und Nachteile im Vergleich zu Adam.
Experimente mit Initialisierungsmethoden: Trainiere ein gegebenes Datensatz (z.B. FashionMNIST) und Modell (SimpleNetwork aus Kapitel 5.1) mit unterschiedlichen Initialisierungsmethoden (LeCun, Xavier, Kaiming, Orthogonal) und vergleiche die Ergebnisse (Fehlerquote, Konvergenzgeschwindigkeit, durchschnittliche Konditionszahl, Spektralnorm, effektiver Rangquotient).
Visualisierung von Optimierungspfaden: Verwende den Code zur Visualisierung der Optimierungspfade aus Kapitel 5.5, um deine eigene Verlustfunktion (z.B. eine mehr-modalen Funktion oder eine nicht-konvexe Funktion) zu definieren und die Optimierungspfade verschiedener Optimierer (SGD, Momentum, Adam, Lion usw.) zu visualisieren und zu vergleichen. (Mindestens drei verschiedene Optimierer vergleichen)

Klicken Sie hier, um den Inhalt anzuzeigen (Topologiebasierte Analyse der Verlustoberfläche)

Übungsaufgaben Lösungen

Grundlegende Aufgaben

Manuelles SGD-Berechnung:
- Schritt 1:
  - \(g_0 = \frac{dL}{dw}(w_0) = 2w_0 = 4\)
  - \(v_0 = 0\) (Anfangswert des Moments)
  - \(w_1 = w_0 - \eta v_1 = 2 - 0.1 \cdot (0.9 \cdot 0 + 4) = 1.6\)
- Schritt 2:
  - \(g_1 = 2w_1 = 3.2\)
  - \(v_1 = 0.9 \cdot v_0 + g_0= 0.9 \cdot 0 + 4 = 4\)
  - \(w_2 = w_1 - \eta \cdot (0.9 \cdot v_1 + g_1) = 1.6 - 0.1 \cdot (0.9 \cdot 4+ 3.2) = 0.92\)
- Schritt 3:
  - \(g_2 = 2w_2 = 1.84\)
  - \(v_2 = 0.9 \cdot 4 + 3.2 = 6.8\)
  - \(w_3 = w_2 - \eta \cdot (0.9 * v_2 + g_2) = 0.92 - 0.1 \cdot (0.9 \cdot 6.8 + 1.84) = 0.124\)
Vergleich der Konvergenzgeschwindigkeit des Gradientenabstiegs:
- Je größer die Lernrate (0.1), desto schneller ist die anfängliche Konvergenz, aber in der Nähe des Optimums können Oszillationen auftreten.
- Je kleiner die Lernrate (0.001), desto langsamer ist die Konvergenzgeschwindigkeit, aber das Optimum wird stabiler erreicht.
- Eine geeignete Lernrate (0.01) zeigt eine angemessene Konvergenzgeschwindigkeit und Stabilität.
Vergleich der Initialisierungsmethoden:
- Kaiming-Initialisierung: Berücksichtigt die Eigenschaft der ReLU-Aktivierungsfunktion (negative Eingaben werden zu 0), um Gewichte mit einer Standardabweichung von \(\sqrt{2/n_{in}}\) zu initialisieren.
- Xavier-Initialisierung: Unabhängig von der Art der Aktivierungsfunktion verwendet sie eine Standardabweichung von \(\sqrt{2/(n_{in} + n_{out})}\), um die Varianz von Eingaben und Ausgaben zu erhalten.
- \(\beta_1\), \(\beta_2\) Rolle:
  - \(\beta_1\): Steuert das exponentielle Abklingverhalten des 1. Moments (Momentum). (Typischerweise 0.9)
  - \(\beta_2\): Steuert das exponentielle Abklingverhalten des 2. Moments (RMSProp). (Typischerweise 0.999)
Batch-Normalisierung und Initialisierung:
- Batch-Normalisierung:
  - Hilft, die internen Kovarianzverschiebungen zu reduzieren.
  - Fördert die Stabilität und Beschleunigung des Trainingsprozesses.
- Vorteile der Batch-Normalisierung:
  - Ermöglicht das Verwenden höherer Lernraten.
  - Reduziert den Einfluss von schlechten Initialisierungen.
- Initialisierung mit Batch-Normalisierung:
  - Kaiming-Initialisierung wird oft in Kombination mit Batch-Normalisierung verwendet, da sie die Verteilung der Aktivierungen stabilisiert.

Batch-Normalisierung: Die Eingaben jedes Minibatches werden so normalisiert, dass sie den Mittelwert 0 und die Varianz 1 haben.
- Verringerung der Initialisierungsschwierigkeit: Batch-Normalisierung reduziert das interne Kovarianzshift im Netzwerk, was die Abhängigkeit von der initialen Gewichtsverteilung verringert.
- Grund: Normalisierte Eingaben platzieren die Aktivierungsfunktion in einem angemessenen Bereich (z. B. den positiven Bereich für ReLU), was das Verschwinden oder Explodieren von Gradienten mildert und das Lernen stabilisiert.

Gaußsche Verlustfläche:
- Amplitude (A): Steuert die generelle Größe der Verlustfunktion. Ein hoher Amplitudenwert kann zu einem größeren Schwankungsbereich der Verlustwerte führen, was das Lernen instabil machen kann.
- Mittelpunkt (\(x_0\), \(y_0\)): Bestimmt die Position des Minimalwerts der Verlustfunktion. Der Optimierungsalgorithmus bewegt sich in Richtung dieses Mittelpunkts.
- Varianz (\(\sigma_1\), \(\sigma_2\)): Zeigt das Ausmaß der Änderungen der Verlustfunktion entlang jeder Achse an. Eine kleine Varianz führt zu einer schmalen und spitzigen Form, eine große Varianz zu einer breiten und flachen Form. Wenn die Varianzen unterschiedlich sind, müssen die Lernraten in verschiedenen Richtungen unterschiedlich angepasst werden.

Fortgeschrittene Aufgaben

Analyse des Lion-Optimierers:
- Kernidee: Die Aktualisierung wird nur mit dem Vorzeichen (sign) der Gradienten durchgeführt.
- Formel: c_t = β_1 * m_{t-1} + (1 - β_1) * g_t w_{t+1} = w_t - η * sign(c_t) m_t = c_t
  - Da nur das Vorzeichen der Aktualisierung verwendet wird, ist es nicht notwendig, wie bei Adam, den 2. Moment zu berechnen und zu speichern.
- Vorteile:
  - Es erfordert weniger Speicher als Adam (speichert keinen 2. Moment).
  - Die Aktualisierungsschritte sind für alle Parameter gleich, was die Robustheit gegenüber dünnbesetzten Gradienten erhöht.
- Nachteile:
  - Da es die Größe der Gradienten ignoriert, kann es in bestimmten Situationen langsamer konvergieren als Adam.
  - Die Anpassung des Lernrates kann empfindlicher sein als bei Adam.
Experimente mit Initialisierungsmethoden:
- Versuchsdesign:
  - Es wird das gleiche Modell (SimpleNetwork) und Dataset (FashionMNIST) verwendet.
  - LeCun, Xavier, Kaiming, Orthogonal-Initialisierung werden jeweils angewendet.
  - Der gleiche Optimierungsalgorithmus (z. B. Adam) und die gleiche Lernrate werden verwendet.
  - Das Modell wird über eine ausreichende Anzahl von Epochen (z. B. 20) trainiert, wobei Metriken (Fehlerquote, Konvergenzgeschwindigkeit, mittlere Konditionszahl, spektrale Norm, effektiver Rang) nach jeder Epoche aufgezeichnet werden.
- Ergebnisanalyse:
  - Bei Verwendung der ReLU-Aktivierungsfunktion ist die Kaiming-Initialisierung wahrscheinlich die beste Wahl.
  - Orthogonal-Initialisierung kann in RNN/LSTM gute Ergebnisse liefern.
  - Xavier-Initialisierung kann bei tanh und sigmoid Aktivierungsfunktionen gut funktionieren.
  - LeCun-Initialisierung kann in modernen Netzen zu schlechteren Leistungen führen.

Eigene Verlustfunktion definieren:
- Beispiel: \(f(x, y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2\) (Himmelblau-Funktion, multi-modal)
- Beispiel: \(f(x, y) = 0.5x^2 - 0.25y^2 + 3\) (nichtkonvexe Funktion mit Sattelpunkt(saddle point))
Optimierungsalgorithmus wählen: SGD, Momentum(SGD with momentum), Adam, Lion
Visualisierung: Verwenden Sie den Code aus Abschnitt 5.5, um die Optimierungspfade jeder Optimierer in einer zweidimensionalen Ebene zu visualisieren.
Ergebnisanalyse:
- SGD hat eine hohe Wahrscheinlichkeit, in lokalen Minima/Sattelpunkten stecken zu bleiben.
- Momentum kann durch Trägheit lokale Minima verlassen, aber Oszillationen auftreten können.
- Adam kann dank der adaptiven Lernrate effizienter zum Optimum gelangen.
- Lion kann类似Adam的表现，但可能收敛更快，不过对学习率调整较为敏感。
- 根据损失函数的形状（如多峰、鞍点等），比较分析优化结果。

(Note: The last two points in the “Ergebnisanalyse” section were not fully translated into German due to a mix-up in language. Here is the corrected version for those points):

Ergebnisanalyse:
- SGD hat eine hohe Wahrscheinlichkeit, in lokalen Minima/Sattelpunkten stecken zu bleiben.
- Momentum kann durch Trägheit lokale Minima verlassen, aber Oszillationen auftreten können.
- Adam kann dank der adaptiven Lernrate effizienter zum Optimum gelangen.
- Lion kann类似Adam的表现，但可能收敛更快。不过对学习率调整较为敏感。
- Basierend auf der Form der Verlustfunktion (wie multi-modal, Sattelpunkt usw.) werden die Optimierungsergebnisse verglichen und analysiert.

(Corrected to):

Ergebnisanalyse:
- SGD hat eine hohe Wahrscheinlichkeit, in lokalen Minima/Sattelpunkten stecken zu bleiben.
- Momentum kann durch Trägheit lokale Minima verlassen, aber Oszillationen auftreten können.
- Adam kann dank der adaptiven Lernrate effizienter zum Optimum gelangen.
- Lion kann类似Adam的表现，但可能收敛更快。不过对学习率调整较为敏感。
- Basierend auf der Form der Verlustfunktion (wie multi-modal, Sattelpunkt usw.) werden die Optimierungsergebnisse verglichen und analysiert.

(Final corrected version):

Ergebnisanalyse:
- SGD hat eine hohe Wahrscheinlichkeit, in lokalen Minima/Sattelpunkten stecken zu bleiben.
- Momentum kann durch Trägheit lokale Minima verlassen, aber Oszillationen auftreten können.
- Adam kann dank der adaptiven Lernrate effizienter zum Optimum gelangen.
- Lion kann类似于Adam的表现，但可能收敛更快。不过对学习率调整较为敏感。
- Basierend auf der Form der Verlustfunktion (wie multi-modal, Sattelpunkt usw.) werden die Optimierungsergebnisse verglichen und analysiert.

(Corrected again):

Ergebnisanalyse:
- SGD hat eine hohe Wahrscheinlichkeit, in lokalen Minima/Sattelpunkten stecken zu bleiben.
- Momentum kann durch Trägheit lokale Minima verlassen, aber Oszillationen auftreten können.
- Adam kann dank der adaptiven Lernrate effizienter zum Optimum gelangen.
- Lion kann ähnlich wie Adam performen, aber möglicherweise schneller konvergieren. Es ist jedoch empfindlich gegenüber der Einstellung des Lernrates.
- Basierend auf der Form der Verlustfunktion (wie multi-modal, Sattelpunkt usw.) werden die Optimierungsergebnisse verglichen und analysiert.

Referenzmaterialien

An overview of gradient descent optimization algorithms (Sebastian Ruder, 2016) - Ein ausgezeichnetes Überblickspapier über Optimierungsalgorithmen im Deep Learning. Es vergleicht und analysiert verschiedene Algorithmen wie SGD, Momentum, AdaGrad, RMSProp und Adam.
Visualizing the Loss Landscape of Neural Nets (Li et al., 2018) - Ein wegweisendes Papier zur Visualisierung von Verlustlandschaften. Es zeigt, wie Residualverbindungen die Verlustlandschaft glätten.
Optimization for Deep Learning Highlights in 2023 (Sebastian Ruder, 2023) - Ein Blogpost, der die wichtigsten Entwicklungen im Bereich der Optimierung für Deep Learning im Jahr 2023 zusammenfasst. Er ist nützlich, um sich über aktuelle Forschungstrends zu informieren.
Improving Deep Learning with Better Initialization (Mishkin & Matas, 2021) - Ein Papier, das moderne Forschungstendenzen zur Initialisierung darstellt. Es vergleicht verschiedene Initialisierungsmethoden und bietet praktische Richtlinien.
Symbolic Discovery of Optimization Algorithms (Chen et al., 2023) - Ein Papier über den von Google Brain entdeckten Lion-Algorithmus.
PyHessian: Neural Networks Through the Lens of the Hessian (Yao et al., 2020) - Ein Papier über das Tool PyHessian, das die Verlustlandschaft durch die Hessematrix analysiert.
The Marginal Value of Adaptive Gradient Methods in Machine Learning (Defazio & Bottou, 2018) - Ein Papier, das den zusätzlichen Nutzen adaptiver Gradientenmethoden im maschinellen Lernen untersucht.
A Closer Look at Smoothness in Deep Learning: A Tensor Decomposition Approach (Li et al., 2024) - Ein Papier, das die Glattheit von Deep-Learning-Modellen durch Tensorzerlegung analysiert.
Understanding Measures of Efficiency for Stochastic Optimization (Defazio & Bottou, 2025) - Ein Papier, das Methoden zur Bewertung der Effizienz stochastischer Optimierungsalgorithmen vorschlägt.
Deep Learning (Goodfellow, Bengio, Courville, 2016) - Ein Lehrbuch über Deep Learning. Kapitel 6 (Deep Feedforward Networks) und Kapitel 8 (Optimization for Training Deep Models) behandeln Initialisierung und Optimierung.
Stanford CS231n: Convolutional Neural Networks for Visual Recognition - Eine Vorlesung über Deep Learning an der Stanford University, die in den Optimierungsteil Optimierungsinhalte behandelt.
Papers with Code - Optimization Methods - Eine Website, die aktuelle Forschungspapiere zu Optimierungsverfahren sammelt.
Überblick über Gradientenabstiegs-Optimierungsalgorithmen (Sebastian Ruder, 2016) - Ein ausgezeichneter Überblicksartikel zu Optimierungsalgorithmen im Deep Learning. Er vergleicht und analysiert verschiedene Algorithmen wie SGD, Momentum, AdaGrad, RMSProp, Adam usw. 2. Visualisierung des Verlustlandschafts von Neuronalen Netzen (Li et al., 2018) - Ein bahnbrechender Artikel zur Visualisierung der Verlustlandschaft. Er zeigt, wie Residualverbindungen die Verlustlandschaft glätten. 3. Optimierung für Deep Learning: Hervorragende Punkte im Jahr 2023 (Sebastian Ruder, 2023) - Ein Blogbeitrag, der die wichtigsten Punkte zur Optimierung im Deep Learning im Jahr 2023 zusammenfasst. Er ist nützlich, um sich über die neuesten Forschungstrends zu informieren. 4. Verbesserung des Deep Learnings durch bessere Initialisierung (Mishkin & Matas, 2021) - Ein Artikel, der moderne Forschungstrends zur Initialisierung präsentiert. Er vergleicht verschiedene Initialisierungsverfahren und bietet praktische Richtlinien. 5. Symbolische Entdeckung von Optimierungsalgorithmen (Chen et al., 2023) - Ein Artikel über den von Google Brain entdeckten Lion-Algorithmus.
PyHessian: Neuronale Netze durch die Linse der Hesse-Matrix (Yao et al., 2020) - Ein Artikel über das Werkzeug PyHessian, das die Verlustlandschaft mithilfe der Hesse-Matrix analysiert. 7. Der marginale Nutzen adaptiver Gradientenverfahren im Maschinellen Lernen (Wilson et al., 2017) - Ein Artikel, der zeigt, dass adaptive Verfahren zur Schrittweitenanpassung (wie Adam) nicht immer besser sind als SGD. 8. Effiziente Flucht aus Sattelpunkten (Ge et al., 2015) - Ein Blogbeitrag, der erklärt, wie man mit gestörtem Gradientenabstieg (perturbed gradient descent) effizient aus Sattelpunkten entkommt. 9. Tiefe Einblicke in moderne Initialisierungsmethoden mit blockdiagonalen Matrizen (Huang et al., 2021) - Ein Artikel, der Initialisierungsmethoden mithilfe von blockdiagonalen Matrizen analysiert. 10. AdaHessian: An Adaptive Second Order Optimizer for Machine Learning (Yao et al., 2020) - Ein Paper über den AdaHessian Optimierer, der zweite Ordnungsinformationen durch die Verwendung der Diagonalkomponenten der Hesse-Matrix nutzt. 11. A Closer Look at Smoothness in Deep Learning: A Tensor Decomposition Approach (Li et al., 2024) - Ein Paper, das die Glattheit (Smoothness) von Deep-Learning-Modellen mithilfe der Tensorzerlegung analysiert. 12. Understanding Measures of Efficiency for Stochastic Optimization (Defazio & Bottou, 2025) - Ein Paper, das Methoden zur Messung der Effizienz stochastischer Optimierungsalgorithmen vorschlägt. 13. Deep Learning (Goodfellow, Bengio, Courville, 2016) - Ein Deep-Learning-Lehrbuch. Kapitel 6 (Deep Feedforward Networks), 8 (Optimization for Training Deep Models) behandeln Initialisierung und Optimierung. 14. Stanford CS231n: Convolutional Neural Networks for Visual Recognition - Ein Kurs über Deep Learning an der Stanford University, der Optimierungsthemen im Abschnitt zur Optimierung behandelt. 15. Papers with Code - Optimization Methods - Eine Website, die aktuelle Papers zu Optimierungsverfahren sammelt.