6. Kapitel: Überanpassung und die Entwicklung von Lösungsverfahren

“Einfachheit ist die ultimative Eleganz.” - Leonardo da Vinci

Deep-Learning-Modelle verfügen über eine starke Fähigkeit, komplexe Funktionen durch zahlreiche Parameter auszudrücken. Diese Fähigkeit kann jedoch manchmal wie ein Doppelschwert sein. Wenn das Modell sich zu sehr an die Trainingsdaten anpasst, tritt die Überanpassung (overfitting) auf, bei der die Vorhersageleistung für neue Daten tatsächlich sinkt.

Nachdem 1986 der Rückpropagationsalgorithmus wiederentdeckt wurde, war Überanpassung eine ständige Herausforderung für Deep-Learning-Forscher. Anfangs reagierte man auf Überanpassung, indem man die Modellgröße reduzierte oder mehr Trainingsdaten hinzufügte. Diese Methoden hatten jedoch Grenzen, da sie die Ausdrucksfähigkeit des Modells einschränkten oder durch Schwierigkeiten bei der Datensammlung beeinträchtigt wurden. 2012 markierte das Erscheinen von AlexNet eine neue Ära für Deep Learning, aber es unterstrich gleichzeitig die Dringlichkeit des Überanpassungsproblems. AlexNet verfügte über viel mehr Parameter als frühere Modelle und damit auch um einiges größere Überanpassungsrisiken. Mit der exponentiellen Vergrößerung von Deep-Learning-Modellen wurde das Überanpassungsproblem zum zentralen Thema in der Forschung.

In diesem Kapitel werden wir die Essenz der Überanpassung verstehen und verschiedene Methoden zur Lösung dieses Problems betrachten, die im Laufe der Zeit entwickelt wurden. Wie Entdecker, die unbekanntes Territorium erforschen und Karten erstellen, haben Deep-Learning-Forscher ständig neue Wege erforscht und verbessert, um das Problem der Überanpassung zu bewältigen.

6.1 Verständnis der Überanpassung

Die Überanpassung wurde erstmals 1670 in William Hopkins’ Schrift erwähnt, aber im modernen Sinne begann sie 1935 im Quarterly Review of Biology mit der Bemerkung “Eine sechsfache Analyse von 13 Beobachtungen sieht wie Überanpassung aus”. Sie wurde ab den 1950er Jahren in der Statistik intensiver untersucht, insbesondere in der Arbeit “Tests of Fit in Time Series” aus dem Jahr 1952 im Kontext der Zeitreihenanalyse.

Das Überanpassungsproblem im Deep Learning nahm eine neue Dimension an, als AlexNet 2012 erschien. AlexNet war ein großes neuronales Netz mit etwa 60 Millionen Parametern und überragte damit die vorherigen Modelle in der Größenordnung. Mit der exponentiellen Vergrößerung von Deep-Learning-Modellen wurde das Überanpassungsproblem immer dringlicher. Zum Beispiel verfügen moderne große Sprachmodelle (LLMs) über Hunderte von Milliarden Parametern, wodurch die Prävention von Überanpassung zu einem zentralen Designziel geworden ist.

Um dieser Herausforderung zu begegnen, wurden innovative Lösungen wie Dropout (2014), Batch-Normalisierung (2015) vorgeschlagen, und in jüngerer Zeit werden fortschrittlichere Methoden zur Erkennung und Verhinderung von Überanpassung durch die Nutzung von Trainingsverläufen (2024) erforscht. Besonders bei großen Modellen werden verschiedene Strategien kombiniert verwendet, von traditionellen Ansätzen wie early stopping bis hin zu modernen Techniken wie Ensemble-Lernen und Datenverstärkung.

Lasst uns ein einfaches Beispiel betrachten, um das Phänomen der Überanpassung intuitiv zu verstehen. Wir wenden Polynome unterschiedlichen Grades auf Daten an, die eine sinusförmige Funktion mit Rauschen enthalten.

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

import numpy as np
import seaborn as sns

# Noisy sin graph
def real_func(x):
    y = np.sin(x) + np.random.uniform(-0.2, 0.2, len(x))
    return y

# Create x data from 40 to 320 degrees.  Use a step value to avoid making it too dense.
x = np.array([np.pi/180 * i for i in range(40, 320, 4)])

y = real_func(x)


import seaborn as sns

sns.scatterplot(x=x, y=y, label='real function')

# Plot with 1st, 3rd, and 21th degree polynomials.  
for deg in [1, 3, 21]:  
# Get the coefficients for the corresponding degree using polyfit, and create the estimated function using poly1d.
    params = np.polyfit(x, y, deg) # Get the parameter values
    # print(f" {deg} params = {params}")
    p = np.poly1d(params) # Get the line function
    sns.lineplot(x=x, y=p(x), color=f"C{deg}", label=f"deg = {deg}")

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

/tmp/ipykernel_1362795/2136320363.py:25: RankWarning: Polyfit may be poorly conditioned
  params = np.polyfit(x, y, deg) # Get the parameter values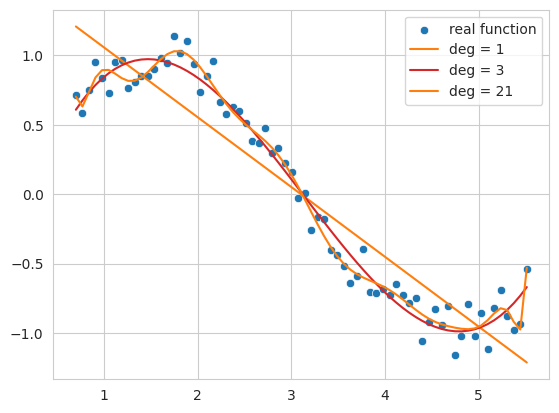

Der folgende Code erstellt Daten einer Sinusfunktion mit Rauschen und passt (fitting) diese Daten mit Polynomen 1. Ordnung, 3. Ordnung und 21. Ordnung an.

• Polynom 1. Ordnung (deg = 1): Es folgt nicht dem allgemeinen Trend der Daten und zeigt eine einfache lineare Form. Dies zeigt einen Zustand von Underfitting, bei dem das Modell die Komplexität der Daten nicht ausreichend darstellt.

• Polynom 3. Ordnung (deg = 3): Es erfasst das grundlegende Muster der Daten ziemlich gut und zeigt eine glatte Kurve, die nicht stark durch Rauschen beeinflusst wird.

• Polynom 21. Ordnung (deg = 21): Es folgt zu sehr dem Rauschen in den Trainingsdaten und zeigt einen Zustand von Overfitting, bei dem das Modell übermäßig an die Trainingsdaten angepasst ist.

So tritt Underfitting auf, wenn die Komplexität des Modells (hier der Grad des Polynoms) zu niedrig ist, und Overfitting, wenn sie zu hoch ist. Letztendlich suchen wir ein Modell, das nicht nur die Trainingsdaten, sondern auch neue Daten gut generalisieren kann, also eine Näherungsfunktion, die dem tatsächlichen Sinus am nächsten kommt.

Overfitting tritt auf, wenn die Komplexität (Kapazität) des Modells im Verhältnis zur Menge der Trainingsdaten relativ groß ist. Neuronale Netze haben aufgrund ihrer vielen Parameter und hohen Ausdrucksstärke eine besondere Anfälligkeit für Overfitting. Wenn die Trainingsdaten knapp sind oder viel Rauschen enthalten, kann Overfitting ebenfalls auftreten. Overfitting zeigt sich durch folgende Merkmale:

• Trainingsdaten: Der Verlust (loss) nimmt stetig ab.
• Validierungsdaten: Der Verlust nimmt zuerst ab und steigt dann ab einem bestimmten Punkt wieder an.
• Dies liegt daran, dass das Modell auch das Rauschen und die feinen Details der Trainingsdaten lernt und daher übermäßig an diese spezialisiert ist.

Letztendlich zeigt ein über angepasstes Modell hohe Leistung auf den Trainingsdaten, fällt aber bei neuen Daten in Bezug auf Vorhersageleistung zurück. Um Overfitting zu vermeiden, werden wir uns im Folgenden mit verschiedenen Techniken wie L1/L2-Regularisierung, Dropout und Batch-Normalisierung näher beschäftigen.

6.2 Regularisierungstechniken

Herausforderung: Wie kann die Generalisierungsleistung verbessert werden, während gleichzeitig die Komplexität des Modells effektiv gesteuert wird?

Überlegungen der Forscher: Das Verkleinern der Modellgröße, um das Overfitting zu verhindern, kann die Ausdrucksfähigkeit einschränken und eine einfache Erhöhung der Trainingsdatenmenge ist nicht immer möglich. Es war notwendig, Methoden zu finden, die durch Einschränkungen an der Struktur oder im Lernprozess des Modells übermäßige Optimierung für die Trainingsdaten verhindern und die Vorhersageleistung für neue Daten verbessern.

6.2.1 L1-, L2-Regularisierung

Typische Regularisierungsverfahren in neuronalen Netzen sind die L1- und L2-Regularisierung. L1 steht für Lasso, L2 für Ridge-Regression (oder lineare Regression mit diesen Techniken).

Sie werden auch als Ridge-Regression und Lasso-Regression bezeichnet, wobei jede eine bestimmte Strafterm einführt, um die Bewegung der Parameter zu begrenzen. Die Unterschiede zwischen den beiden Methoden können in folgender Tabelle zusammengefasst werden:

Merkmal	Ridge-Regression (Ridge Regression)	Lasso-Regression (Lasso Regression)
Strafarten	L2-Strafe anwenden. Der Strafterm ist das Produkt des Quadrats der Parameter und des Alpha-Werts.	L1-Strafe anwenden. Der Strafterm ist das Produkt der absoluten Werte der Parameter und des Alpha-Werts.
Einfluss auf die Parameter	Dämpft große Parameter, sodass sie nahe bei 0 liegen (aber nie exakt 0).	Bei hohen Alpha-Werten kann es dazu führen, dass einige Parameterwerte exakt 0 werden, was zu einem vereinfachten Modell führt.
Gesamt-Einfluss	Alle Parameter bleiben erhalten; auch solche mit geringerem Einfluss bleiben bestehen.	Nur relevante Parameter bleiben übrig und die Methode besitzt selektive Eigenschaften, was dazu beiträgt, komplexe Modelle einfacher zu beschreiben.
Optimierungseigenschaften	Weniger empfindlich gegenüber idealen Werten im Vergleich zu Lasso.	Aufgrund des absoluten Wertes der Strafterme ist die Methode empfindlicher gegenüber idealen Werten.

Die mathematischen Darstellungen sehen wie folgt aus:

• Ridge-Zielfunktion (Ridge Regression Objective Function)

  “Modifizierte Ridge-Zielfunktion” = (unmodifizierte lineare Regressionsfunktion) + \(\alpha \cdot \sum (\text{Parameter})^2\)

  \(f_{\beta} = \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} \beta_{j}^2\)

  Hierbei ist \(\beta\) der zu bestimmende Parameter-Vektor (Gewichte). \(\alpha \sum_{j} \beta_{j}^2\) wird als Strafterm oder Regularisierungsterm bezeichnet. \(\alpha\) ist ein Hyperparameter, der die Stärke des Regularisierungsterms steuert. Die Formel zur Bestimmung der Parameter lautet:

  \(\beta = \underset{\beta}{\operatorname{argmin}} \left( \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} \beta_{j}^2 \right)\)

• Lasso-Zielfunktion (Lasso Regression Objective Function)

  “Modifizierte Lasso-Zielfunktion” = (unmodifizierte lineare Regressionsfunktion) + $ || $

  \(f_{\beta} = \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} |\beta_{j}|\) \(\beta = \underset{\beta}{\operatorname{argmin}} \left( \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} |\beta_j| \right)\)

Die Summe der Quadrate der Parameter als Strafterm zu verwenden, wird in neuronalen Netzen häufig als Gewichtsverfall (weight decay) bezeichnet. Wir werden untersuchen, wie sich die Verwendung von Ridge-Regression (L2) im Vergleich zur einfachen linearen Regression unterscheidet. Dafür verwenden wir ein Modell, das in sklearn implementiert ist. Dazu müssen wir die Eingabedaten x so verarbeiten, dass sie um die entsprechende Anzahl von Dimensionen erweitert werden. Wir werden dies mit der folgenden einfachen Utility-Funktion tun.

def get_x_powered(x, p=1):
    size = len(x)

    # The shape of the created x will be (data size, degree)
    new_x = np.zeros((size, p))

    for s in range(len(x)): # Iterate over data size
        for d in range(1, p+1): # Iterate over degrees
            new_x[s][d-1] = x[s]**d # Raise x to the power of the degree.

    return new_x


# Let's take a quick look at how it works.
deg = 3
x = np.array([np.pi/180 * i for i in range(20, 35, 5)])
y = real_func(x)  # real_func는 이전 코드에 정의되어 있다고 가정

print(f"x = {x}")
new_x = get_x_powered(x, p=deg)

print(f"new_x = {new_x}")

x = [0.34906585 0.43633231 0.52359878]
new_x = [[0.34906585 0.12184697 0.04253262]
 [0.43633231 0.19038589 0.08307151]
 [0.52359878 0.27415568 0.14354758]]

Da es sich um eine dritte Ordnung handelt, erhöhen sich die \(x\)-Werte zu \(x^2, x^3\). Zum Beispiel 0.3490, 0.1218 (Quadrat von 0.3490), 0.04253 (Kubik von 0.3490). Wenn es sich um eine zehnte Ordnung handelt, werden die Daten bis \(x^{10}\) generiert. Der Alphawert des Strafterms kann Werte von null bis unendlich annehmen. Je größer der Alphawert ist, desto stärker ist die Regularisierung. Wir werden den Grad auf 13 festlegen und die lineare Regression mit Ridge-Regression bei unterschiedlichen Alphawerten vergleichen.

import numpy as np
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# Create a noisy sine wave (increased noise)
def real_func(x):
    return np.sin(x) + np.random.normal(0, 0.4, len(x))  # Increased noise

# Create x data (narrower range)
x = np.array([np.pi / 180 * i for i in range(40, 280, 8)])  # Narrower range, larger step

y = real_func(x)

# Degree of the polynomial
deg = 10

# List of alpha values to compare (adjusted)
alpha_list = [0.0, 0.1, 10]  # Adjusted alpha values
cols = len(alpha_list)

fig, axes_list = plt.subplots(1, cols, figsize=(20, 5))  # Adjusted figure size

for i, alpha in enumerate(alpha_list):
    axes = axes_list[i]

    # Plot the original data
    sns.scatterplot(ax=axes, x=x, y=y, label='real function', s=50)  # Increased marker size

    # Plot linear regression
    params = np.polyfit(x, y, deg)
    p = np.poly1d(params)
    sns.lineplot(ax=axes, x=x, y=p(x), label=f"LR deg = {deg}")

    # Ridge regression (using Pipeline, solver='auto')
    model = make_pipeline(PolynomialFeatures(degree=deg), Ridge(alpha=alpha, solver='auto'))
    model.fit(x.reshape(-1, 1), y)  # Reshape x for pipeline
    y_pred = model.predict(x.reshape(-1, 1)) # Reshape x for prediction
    sns.lineplot(ax=axes, x=x, y=y_pred, label=f"Ridge alpha={alpha:0.1e} deg={deg}")

    axes.set_title(f"Alpha = {alpha:0.1e}")
    axes.set_ylim(-1.5, 1.5)  # Limit y-axis range
    axes.legend()

plt.tight_layout()
plt.show()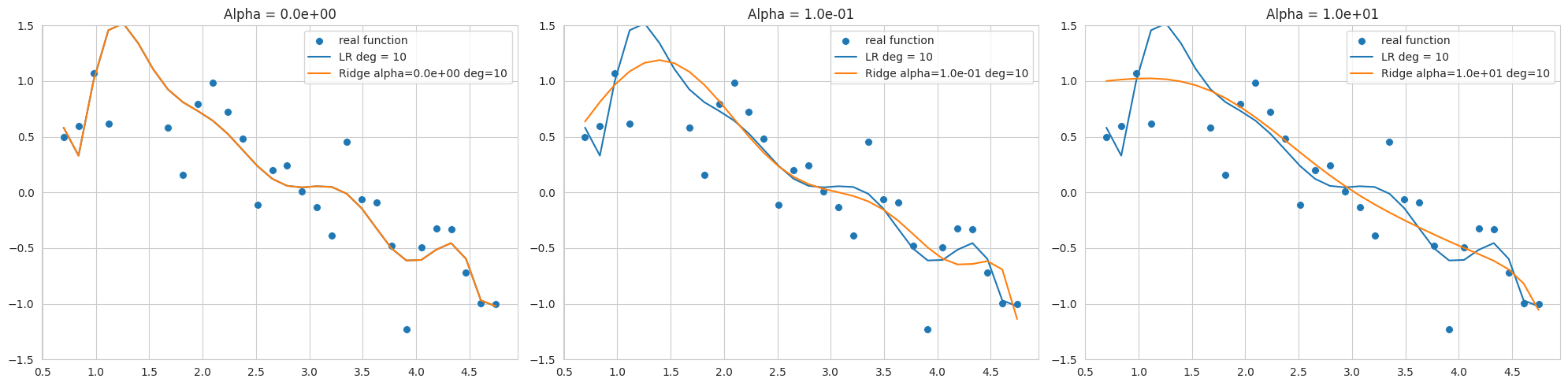

Das obige Diagramm zeigt die Ergebnisse des Fittings von Sinusfunktionsdaten mit hinzugefügtem Rauschen unter Verwendung eines Polynoms 10. Grades, wobei Ridge-Regression mit unterschiedlichen alpha Werten (Regularisierungsstärke) dargestellt wird. Da der Datenbereich eng und das Rauschen hoch ist, kann Overfitting selbst bei niedrigen Graden leicht auftreten.

• Alpha = 0.0: Die Ridge-Regression entspricht der gewöhnlichen linearen Regression mit kleinsten Quadraten, und das Polynom 10. Grades folgt sogar den Rauschen in den Trainingsdaten, was zu einem stark überangepassten Muster führt.
• Alpha = 0.1: Eine schwache Regularisierung wird angewendet, wodurch die Anzahl der Kurven im Vergleich zu alpha=0 reduziert wird, jedoch bleibt es noch empfindlich gegenüber Rauschen und weicht vom Sinusfunktion ab.
• Alpha = 10: Durch starke Regularisierung wird die Kurve viel glatter, was den allgemeinen Trend der Daten (Sinusfunktion) gut wiedergibt. Dies zeigt, dass L2-Regularisierung (Ridge-Regression) das Overfitting effektiv kontrollieren kann.

Durch eine geeignete Auswahl des alpha Wertes kann die Modellkomplexität gesteuert und die Verallgemeinerungsleistung verbessert werden. L2-Regularisierung ist nützlich, da sie die Gewichte nahe an Null hält und das Modell stabilisiert.

Das sklearn.linear_model.Ridge Modell kann je nach gewähltem solver unterschiedliche Optimierungsverfahren verwenden. Insbesondere bei engen Datenbereichen mit viel Rauschen, wie in diesem Beispiel, können 'svd' oder 'cholesky' Solver stabiler sein, so dass bei der Auswahl des Solvers Vorsicht geboten ist (im Code wird 'cholesky' verwendet).

6.2.2 Anwendung von L1 und L2 Regularisierung in PyTorch

PyTorch und Keras unterscheiden sich darin, wie sie L1- und L2-Regularisierung implementieren. Keras unterstützt die direkte Hinzufügung von Regularisierungstermen zu jeder Schicht (kernel_regularizer, bias_regularizer).

# In Keras, you can specify regularization when declaring a layer.
keras.layers.Dense(64, activation='relu',
                    kernel_regularizer=regularizers.l2(0.01),
                    input_shape=(784,))

Im Gegensatz dazu wendet PyTorch L2-Regularisierung durch die Einstellung des Gewichtsverfalls (weight decay) im Optimierer (optimizer) an und implementiert L1-Regularisierung in der Regel über benutzerdefinierte Verlustfunktionen.

import torch.nn as nn
import torch

def custom_loss(outputs, targets, model, lambda_l1=0.01, lambda_l2=0.01,):
    mse_loss = nn.MSELoss()(outputs, targets)
    
    l1_loss = 0.
    l2_loss = 0.
    for param in model.parameters():
        l1_loss += torch.sum(torch.abs(param)) # Take the absolute value of the parameters.
        l2_loss += torch.sum(param ** 2)  # Square the parameters.
    
    total_loss = mse_loss + lambda_l1 * l1_loss + lambda_l2 * l2_loss # Add L1 and L2 penalty terms to the loss.
    return total_loss

# Example usage within a training loop (not runnable as is)
# for inputs, targets in dataloader:
#     # ... (rest of the training loop)
#     loss = custom_loss(outputs, targets, model)
#     loss.backward()
    # ... (rest of the training loop)

Wie im obigen Beispiel gezeigt, kann die custom_loss-Funktion definiert werden, um sowohl L1- als auch L2-Regularisierung anzuwenden. Allerdings wird in der Regel das weight_decay, das der L2-Regularisierung entspricht, im Optimizer festgelegt und verwendet. Bei den Optimizern Adam und SGD wird die Gewichtsverringerung jedoch etwas anders implementiert als die traditionelle L2-Regularisierung. Die traditionelle L2-Regularisierung fügt dem Verlustfunktionsterm das Quadrat der Parameter hinzu.

\(L_{n+1} = L_{n} + \frac{ \lambda }{2} \sum w^2\)

Die Ableitung davon nach den Parametern ergibt folgendes:

\(\frac{\partial L_{n+1}}{\partial w} = \frac{\partial L_{n}}{\partial w} +\lambda w\)

SGD und Adam implementieren dies, indem sie den Term \(\lambda w\) direkt zur Gradientenaddition verwenden. Der Code für chapter_05/optimizers/ SGD sieht wie folgt aus.

if self.weight_decay != 0:
    grad = grad.add(p, alpha=self.weight_decay)

Dieses Verfahren hat genau die gleiche Wirkung wie das Hinzufügen eines L2-Regulierungs TERMS zum Verlustfunktion, wenn es mit Momentum oder adaptiven Lernraten kombiniert wird.

Trennung von AdamW und Gewichtsabkling (Decoupled Weight Decay)

In dem 2017 auf der ICLR veröffentlichten Papier “Fixing Weight Decay Regularization in Adam” (https://arxiv.org/abs/1711.05101) wird das Problem angesprochen, dass die Gewichtsabkling im Adam-Optimierer anders als L2-Regulierung funktioniert, und der modifizierte AdamW-Optimierer vorgeschlagen wird. In AdamW wird die Gewichtsabkling von den Gradientenupdates getrennt und direkt im Schritt der Parameteraktualisierung angewendet. Der Code befindet sich in derselben Datei basic.py.

# PyTorch AdamW weght decay
if weight_decay != 0:
    param.data.mul_(1 - lr * weight_decay)

AdamW multipliziert die Parameterwerte mit 1 - lr * weight_decay.

• Gewichtsabkling von Adam: Im Schritt der Gradientenaktualisierung wird der Gewichtsabkling-Term (\(\lambda w\)) zusammen mit der Lernrate (\(lr\)) und anderen Gradientenanpassungstermen (z. B. Momentum) berücksichtigt. Dadurch kann die Wirkung des Gewichtsabklings von der Lernrate und den Einstellungen anderer Hyperparameter abhängen.
• Gewichtsabkling bei AdamW: Da die Gewichtsabkling separat im Schritt der Parameteraktualisierung angewendet wird, ist sie weniger abhängig von der Lernrate oder anderen Hyperparametern. Dies bedeutet, dass die Wirkung der Gewichtsabkling vorhersagbarer und konsistenter ist.

Zusammenfassend lässt sich sagen, dass AdamWs Ansatz einer genauen Implementierung der L2-Regulierung näher kommt. Obwohl die Gewichtsabkling bei SGD und Adam oft als L2-Regulierung bezeichnet wird, liegt dies an historischen Gründen und ähnlichen Effekten; streng genommen ist es jedoch korrekter, sie als separate Regularisierungstechniken zu betrachten. AdamW klärt diese Unterschiede und bietet dadurch bessere Leistung.

6.2.3 Analyse der Regularisierungswirkung in der Verlustfläche

Um den Einfluss von L1- und L2-Regularisierung auf das Lernen des Modells visuell zu verstehen, werden wir die in Kapitel 4 vorgestellte Technik zur Visualisierung der Verlustfläche (loss surface) anwenden. Wir vergleichen die Änderungen der Verlustfläche bei fehlender Regularisierung und bei Anwendung von L2-Regularisierung und beobachten die Verschiebung der optimalen Lösung in Abhängigkeit von der Regularisierungsstärke (weight_decay).

import sys

from dldna.chapter_05.visualization.loss_surface import xy_perturb_loss,  hessian_eigenvectors, visualize_loss_surface 
from dldna.chapter_04.utils.data import get_dataset, get_device   
from dldna.chapter_04.utils.metrics import load_model  

import torch
import torch.nn as nn
import numpy as np
import torch.utils.data as data_utils
from torch.utils.data import  DataLoader


device = get_device()  # Get the device (CPU or CUDA)
train_dataset, test_dataset = get_dataset()  # Load the datasets.  

act_name = "ReLU"
model_file = f"SimpleNetwork-{act_name}.pth"

small_dataset = data_utils.Subset(test_dataset, torch.arange(0, 256))  # Use a subset of the test dataset
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)  # Create a data loader
loss_func = nn.CrossEntropyLoss()  # Define the loss function

# Load the trained model.
trained_model, _ = load_model(model_file=model_file, path="./tmp/opts/ReLU") # 4장의 load_model 사용
trained_model = trained_model.to(device)  # Move the model to the device

top_n = 2  # Number of top eigenvalues/eigenvectors to compute
top_eigenvalues, top_eigenvectors =  hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True)  # 5장의 함수 사용

d_min ,d_max, d_num = -1, 1, 50  # Define the range and number of points for the grid
lambda1, lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32), np.linspace(d_min, d_max, d_num).astype(np.float32)  # Create the grid of lambda values
x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eigenvectors, data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device) # 5장의 함수 사용

xy_perturb_loss wird verwendet, um eine Näherungsfunktion zu erstellen. Danach werden (x,y) in diese Näherungsfunktion eingesetzt, um einen neuen z-Wert zu berechnen. Der Grund dafür ist, dass die Werte, die mit xy_perturb_loss berechnet wurden, wie im Kapitel 5 gezeigt, Konturlinien erzeugen, bei denen der Minimalwert leicht abweicht und der Optimierer an einem leicht unterschiedlichen Punkt konvergiert. Jetzt werden nicht alle Pfade, auf denen der Optimierer verläuft, dargestellt, sondern nur der letzte tiefste Punkt wird verglichen, wobei der Dämpfungsparameter weight_decay schrittweise erhöht wird.

import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim  # Import optim
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, Subset

# 5장, 4장 함수들 import
from dldna.chapter_05.visualization.loss_surface import (
    hessian_eigenvectors,
    xy_perturb_loss,
    visualize_loss_surface
)
from dldna.chapter_04.utils.data import get_dataset, get_device
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.visualization.gaussian_loss_surface import (
    get_opt_params,
    train_loss_surface,
    gaussian_func # gaussian_func 추가.
)


device = get_device()
_, test_dataset = get_dataset(dataset="FashionMNIST") 
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

act_name = "ReLU" # Tanh로 실험하려면 이 부분을 변경
model_file = f"SimpleNetwork-{act_name}.pth"
trained_model, _ = load_model(model_file=model_file, path="./tmp/opts/ReLU") 
trained_model = trained_model.to(device)

top_n = 2
top_eigenvalues, top_eigenvectors = hessian_eigenvectors(
    model=trained_model,
    loss_func=loss_func,
    data_loader=data_loader,
    top_n=top_n,
    is_cuda=True
)

d_min, d_max, d_num = -1, 1, 30 # 5장의 30을 사용
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)

x, y, z = xy_perturb_loss(
    model=trained_model,
    top_eigenvectors=top_eigenvectors,
    data_loader=data_loader,
    loss_func=loss_func,
    lambda1=lambda1,
    lambda2=lambda2,
    device=device # device 추가
)


# --- Optimization and Visualization ---

# Find the parameters that best fit the data.
popt, _, offset = get_opt_params(x, y, z)  # offset 사용

print(f"Optimal parameters: {popt}")

# Get a new z using the optimized surface function (Gaussian).
# No need for global g_offset, we can use the returned offset.
z_fitted = gaussian_func((x, y), *popt,offset) # offset을 더해야 함.


data = [(x, y, z_fitted)]  # Use z_fitted

axes = visualize_loss_surface(data, act_name=act_name, color="C0", size=6, levels=80, alpha=0.7, plot_3d=False)
ax = axes[0]

# Train with different weight decays and plot trajectories.
for n, weight_decay in enumerate([0.0, 6.0, 10.0, 18.0, 20.0]):
# for n, weight_decay in enumerate([0.0]):  # For faster testing
    points_sgd_m = train_loss_surface(
        lambda params: optim.SGD(params, lr=0.1, momentum=0.7, weight_decay=weight_decay),
        [d_min, d_max],
        200,
        (*popt, offset) # unpack popt and offset
    )
    ax.plot(
        points_sgd_m[-1, 0],
        points_sgd_m[-1, 1],
        color=f"C{n}",
        marker="o",
        markersize=10,
        zorder=2,
        label=f"wd={weight_decay:0.1f}"
    )
    ax.ticklabel_format(axis='both', style='scientific', scilimits=(0, 0))

plt.legend()
plt.show()

Function parameters = [ 4.59165436  0.34582255 -0.03204057 -1.09810435  1.54530407]
Optimal parameters: [ 4.59165436  0.34582255 -0.03204057 -1.09810435  1.54530407]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[-0.8065, 0.9251]
SGD: Iter=200 loss=1.9090 w=[0.3458, -0.0320]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[-0.2065, 0.3251]
SGD: Iter=200 loss=1.9952 w=[0.1327, -0.0077]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[0.1935, -0.0749]
SGD: Iter=200 loss=2.0293 w=[0.0935, -0.0051]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[0.9935, -0.8749]
SGD: Iter=200 loss=2.0641 w=[0.0587, -0.0030]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[1.1935, -1.0749]
SGD: Iter=200 loss=2.0694 w=[0.0537, -0.0027]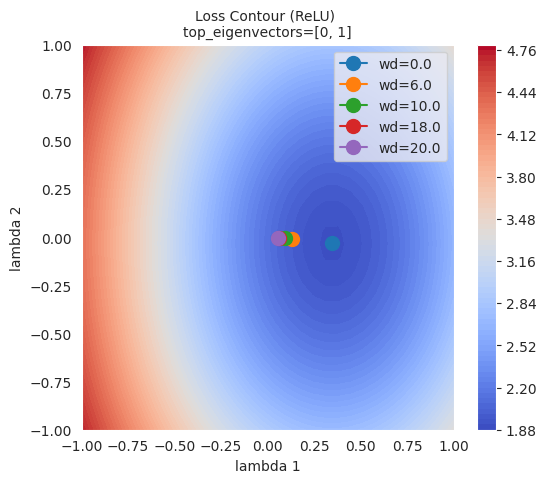

Wie in der Abbildung zu sehen ist, kann beobachtet werden, dass je größer die L2-Regulierung (Weight Decay) ist, desto weiter entfernt sich der Endpunkt, den der Optimizer erreicht hat, vom tiefsten Punkt der Verlustfunktion. Dies liegt daran, dass die L2-Regulierung verhindert, dass die Gewichte zu groß werden, um das Überanpassen des Modells zu vermeiden.

Die L1-Regulierung erstellt ein sparsames Modell (sparse model), indem sie einige Gewichte auf 0 setzt. Sie ist nützlich, wenn man die Komplexität des Modells reduzieren und unnötige Merkmale eliminieren möchte. Im Gegensatz dazu sorgt die L2-Regulierung dafür, dass alle Gewichte klein gehalten werden, aber nicht vollständig auf 0 gesetzt werden. Die L2-Regulierung zeigt im Allgemeinen eine stablilere Konvergenz und wird daher als „weiche Regulierung“ bezeichnet, da sie die Gewichte allmählich reduziert.

L1-Regulierung und L2-Regulierung werden je nach den Eigenschaften des Problems, den Daten und dem Ziel des Modells unterschiedlich angewendet. Obwohl im Allgemeinen die L2-Regulierung häufiger verwendet wird, kann es sinnvoll sein, beide Regulierungen zu testen und zu prüfen, welche bessere Leistungsresultate liefert. Darüber hinaus kann auch die Elastic Net-Regulierung, eine Kombination von L1- und L2-Regulierung, in Betracht gezogen werden.

Klicken Sie hier, um den Inhalt anzuzeigen (Tiefgang: Elastic Net Regularisierung – die Harmonie von L1 und L2)

Elastic Net Regularisierung - Harmonie von L1 und L2

Elastic Net ist eine Regularisierungs-Methode, die L1-Regulierung und L2-Regulierung kombiniert. Sie nutzt die Vorteile beider Regulierungen und kompensiert ihre Nachteile, um flexiblere und effektivere Modelle zu erstellen.

Kernpunkte:

• L1-Regulierung (Lasso): Beschränkt die Summe der Beträge der Gewichte. Sie setzt einige Gewichte genau auf 0, um ein spärliches (sparse) Modell zu erzeugen. Es hat einen Effekt der Merkmalsauswahl (feature selection), indem es unnötige Merkmale entfernt und das Modell vereinfacht.
• L2-Regulierung (Ridge): Beschränkt die Summe der Quadrate der Gewichte. Sie hält alle Gewichte klein, um Überanpassung (overfitting) des Modells zu verhindern. Die Konvergenz ist stabil und die Gewichte werden sanft reduziert.
• Elastic Net: Wendet L1-Regulierung und L2-Regulierung gleichzeitig an. Es kann die Effekte beider Regulierungen erlangen.

Formel:

Die Kostenfunktion von Elastic Net wird wie folgt ausgedrückt:

\(Cost = Loss + \lambda_1 \sum_{i} |w_i| + \lambda_2 \sum_{i} (w_i)^2\)

• Loss: Die Verlustfunktion des ursprünglichen Modells (z.B. MSE, Cross-Entropy)
• λ₁: Hyperparameter zur Anpassung der Stärke der L1-Regulierung
• λ₂: Hyperparameter zur Anpassung der Stärke der L2-Regulierung
• wᵢ: Gewichte des Modells

Vorteile:

• Merkmalsauswahl + Überanpassungsverhinderung: Es kann sowohl den Effekt der Merkmalsauswahl durch L1-Regulierung als auch die Verhinderung von Überanpassung durch L2-Regulierung erlangen.
• Verarbeitung hoch korrelierter Merkmale: L1-Regulierung neigt dazu, eines von mehreren stark korrelierten Merkmalen auszuwählen und die anderen auf 0 zu setzen. Elastic Net mildert dieses Problem durch L2-Regulierung, indem es dazu neigt, stark korrelierte Merkmale zusammen auszuwählen oder zusammen zu entfernen.
• Flexibilität: Die Gewichte von L1- und L2-Regulierung können durch Anpassung von λ₁ und λ₂ gesteuert werden. Bei λ₁=0 wird es zur L2-Regulierung (Ridge), bei λ₂=0 zur L1-Regulierung (Lasso).

Nachteile:

• Hyperparameter-Tuning: Es müssen zwei Hyperparameter, λ₁ und λ₂, eingestellt werden, was das Tuning komplizierter machen kann als bei L1- oder L2-Regulierung.
• Berechnungsaufwand: Da sowohl L1- als auch L2-Regulierung gleichzeitig berechnet werden müssen, kann der Berechnungsaufwand leicht höher sein (in modernen Maschinellem Lernen kein großes Problem).

Anwendungsfälle:

• Wenn viele Merkmale (features) vorhanden sind und davon angenommen wird, dass nur einige wichtig sind (Merkmalsauswahl erforderlich)
• Wenn zwischen den Merkmalen hohe Korrelationen bestehen
• Wenn unklar ist, ob L1-Regulierung oder L2-Regulierung besser geeignet ist (beide ausprobieren wollen)
• Wenn eine Überanpassung verhindert und gleichzeitig ein spärliches Modell erstellt werden soll

Zusammenfassung: Elastic Net ist eine leistungsfähige Regularisierungsmethode, die die Vorteile von L1 und L2 kombiniert. Obwohl es Hyperparameter-Tuning erfordert, kann es in verschiedenen Problemen gute Leistungen zeigen.

6.3 Dropout

6.3.1 Prinzip von Dropout

Dropout ist eine der leistungsfähigsten Regularisierungsmethoden, um Overfitting in neuronalen Netzen zu verhindern. Während des Lernprozesses werden zufällige Neuronen deaktiviert (dropout), um die Übereinstimmung bestimmter Neuronen oder Kombinationen von Neuronen mit den Trainingsdaten zu reduzieren. Dies hat eine ähnliche Wirkung wie Ensemble-Lernen, bei dem verschiedene Personen unterschiedliche Aspekte lernen und sich dann zusammenfassen, um das Problem zu lösen. Es fördert die unabhängige Lernung wichtiger Merkmale durch jedes Neuron, was die Generalisierungsfähigkeit des Modells verbessert. Im Allgemeinen wird es auf vollständig verbundene Schichten (fully connected layer) angewendet und der Deaktivierungsrate liegt zwischen 20% und 50%. Dropout wird nur während des Trainings angewendet, während bei der Inferenz alle Neuronen verwendet werden.

6.3.2 Implementierung von Dropout in PyTorch

In PyTorch kann Dropout wie folgt einfach implementiert werden.

import torch.nn as nn

class Dropout(nn.Module):
    def __init__(self, dropout_rate):
        super(Dropout, self).__init__()
        self.dropout_rate = dropout_rate

    def forward(self, x):
        if self.training:
            mask = torch.bernoulli(torch.ones_like(x) * (1 - self.dropout_rate)) / (1 - self.dropout_rate)
            return x * mask
        else:
            return x

# Usage example.  Drops out 0.5 (50%).
dropout = Dropout(dropout_rate=0.5)

# Example input data
inputs = torch.randn(1000, 100)

# Forward pass (during training)
dropout.train()
outputs_train = dropout(inputs)

# Forward pass (during inference)
dropout.eval()
outputs_test = dropout(inputs)

print("Input shape:", inputs.shape)
print("Training output shape:", outputs_train.shape)
print("Test output shape", outputs_test.shape)
print("Dropout rate (should be close to 0.5):", 1 - torch.count_nonzero(outputs_train) / outputs_train.numel())

Input shape: torch.Size([1000, 100])
Training output shape: torch.Size([1000, 100])
Test output shape torch.Size([1000, 100])
Dropout rate (should be close to 0.5): tensor(0.4997)

Die Implementierung ist sehr einfach. Den mask-Wert mit dem Eingabetensor multiplizieren, um bestimmte Neuronen zu deaktivieren. Die Dropout-Schicht besitzt keine eigenen lernbaren Parameter und hat die einfache Aufgabe, einen Teil der Eingaben zufällig auf 0 zu setzen. In realen neuronalen Netzen wird die Dropout-Schicht zwischen anderen Schichten (z.B. lineare Schichten, Faltungsschichten) eingefügt. Während des Trainings werden Neuronen bei Dropout zufällig entfernt, während bei der Inferenz alle Neuronen verwendet werden. Dabei wird zur Angleichung der Skalierung von Ausgabewerten beim Training und bei der Inferenz die inverted dropout Methode eingesetzt. Inverted Dropout skaliert während des Trainings voraus, indem es durch (1 - dropout_rate) dividiert, sodass es bei der Inferenz ohne zusätzliche Berechnungen direkt angewendet werden kann. Dies ermöglicht es, bei der Inferenz ähnliche Effekte wie beim Ensemble-Lernen zu erzielen. Das heißt, es liefert Effekte, als würden mehrere Teilnetze (sub-networks) durchschnittlich berechnet, und steigert gleichzeitig die Berechnungseffizienz.

Um zu sehen, wie effektiv Dropout ist, betrachten wir ein einfaches Datenbeispiel in einem Diagramm. Der Quellcode befindet sich in chapter_06/plot_dropout.py, und da es sich um unwichtigen Code handelt, wird er hier nicht dargestellt. Da der Code ausführlich kommentiert ist, sollte er einfach zu verstehen sein. Das Diagramm zeigt, dass das Modell mit Dropout (blau) eine viel höhere Testgenauigkeit aufweist.

from dldna.chapter_06.plot_dropout import plot_dropout_effect

plot_dropout_effect()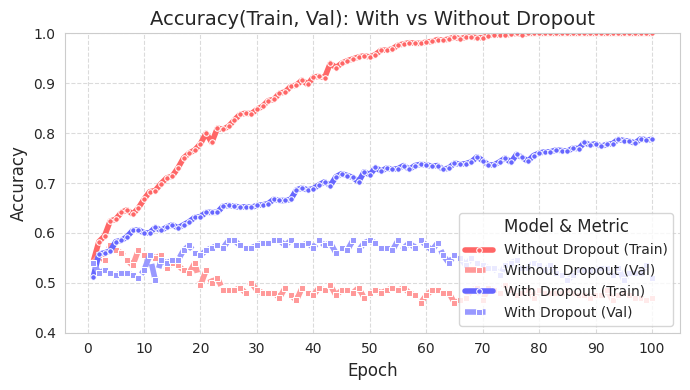

Die Trainingsgenauigkeit des Modells mit Dropout (With Dropout) ist niedriger als die des Modells ohne Dropout (Without Dropout), aber die Validierungs-genauigkeit ist höher. Dies bedeutet, dass Dropout das Overfitting auf die Trainingsdaten reduziert und die Generalisierungsfähigkeit des Modells verbessert.

6.4 Batch-Normalisierung

6.4.1 Konzept und Effekte der Batch-Normalisierung

Batch-Normalisierung ist eine Methode, die gleichzeitig die Rolle einer Regularisierung spielt und die Stabilität der Daten während des Trainings verbessert. Batch-Normalisierung wurde erstmals in einem Paper von Ioffe und Szegedy [Referenz 2] im Jahr 2015 vorgeschlagen. In Deep Learning ändert sich die Verteilung der Aktivierungen, wenn Daten durch jede Schicht fließen (internal covariate shift). Dies verlangsamt das Training und macht das Modell instabil (wegen der Veränderung der Verteilung werden mehr Berechnungsschritte benötigt). Je tiefer die Schichten sind, desto schlimmer wird dieses Problem. Batch-Normalisierung normalisiert die Daten in Mini-Batch-Größe, um dies zu lindern.

Das Kernkonzept der Batch-Normalisierung ist die Normalisierung der Daten in Mini-Batch-Größe. Das folgende Codebeispiel macht dies verständlich.

# Calculate the mean and variance of the mini-batch
batch_mean = x.mean(dim=0)
batch_var = x.var(dim=0, unbiased=False)

# Perform normalization
x_norm = (x - batch_mean) / torch.sqrt(batch_var + epsilon)

# Apply scale and shift parameters
y = gamma * x_norm + beta

Allgemein führt die Batch-Normalisierung zu einer angemessenen Verteilungsänderung der gesamten Daten innerhalb eines Minibatches, indem sie die Varianz und den Mittelwert der Daten verwendet. Zuerst wird eine Normalisierung durchgeführt, gefolgt von der Anwendung einer bestimmten Skalierungs- und Verschiebungseingenschaft. Der oben genannte Gamma ist der Skalierungsparameter und Beta ist der Verschiebungsparameter. Es ist hilfreich, einfach \(y = ax + b\) zu betrachten. Das Epsilon, das während der Normalisierung verwendet wird, ist ein sehr kleiner Konstantwert (1e-5 oder 1e-7), der häufig in numerischer Analyse vorkommt. Dieser Wert dient der numerischen Stabilität. Die Batch-Normalisierung bietet die folgenden zusätzlichen Vorteile.

• Verbesserung der Lernrate: Durch die Stabilisierung der Aktivierungswerteverteilung in jeder Schicht werden Probleme mit Gradientenverschwinden/explodierenden Gradienten gemildert, und es ist möglich, größere Lernraten zu verwenden.
• Verringerung der Abhängigkeit von der Initialisierung: Sie macht die Gewichtsinitialisierung weniger empfindlich, so dass das Lernen einfacher gestartet werden kann.
• Regularisierungs-Effekt: Da Statistiken auf Minibatch-Ebene berechnet werden, wird ein wenig Rauschen hinzugefügt, was überfitting verhindern hilft. (Die Verwendung mit Dropout führt zu besseren Ergebnissen.)

Lassen Sie uns zufällige Daten mit zwei Merkmalen erzeugen und diese sowohl in einem Fall ohne Skalierung und Verschiebung als auch in einem Fall mit angewendeten Skalierungs- und Verschiebungsparametern grafisch vergleichen. Durch die Visualisierung kann man leicht verstehen, welche numerische Bedeutung die Normalisierung innerhalb eines Minibatches hat.

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Generate data
np.random.seed(42)
x = np.random.rand(50, 2) * 10

# Batch normalization (including scaling parameters)
def batch_normalize(x, epsilon=1e-5, gamma=1.0, beta=0.0):
    mean = x.mean(axis=0)
    var = x.var(axis=0)
    x_norm = (x - mean) / np.sqrt(var + epsilon)
    x_scaled = gamma * x_norm + beta
    return x_norm, mean, x_scaled

# Perform normalization (gamma=1.0, beta=0.0 is pure normalization)
x_norm, mean, x_norm_scaled = batch_normalize(x, gamma=1.0, beta=0.0)
# Perform normalization and scaling (apply gamma=2.0, beta=1.0)
_, _, x_scaled = batch_normalize(x, gamma=2.0, beta=1.0)

# Set Seaborn style
sns.set_style("whitegrid")
sns.set_context("notebook", font_scale=1.2)

# Visualization
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))

# Original data
sns.scatterplot(x=x[:, 0], y=x[:, 1], ax=ax1, color='royalblue', alpha=0.7)
ax1.scatter(mean[0], mean[1], color='red', marker='*', s=200, label='Mean')
ax1.set(title='Original Data',
        xlabel='Feature 1',
        ylabel='Feature 2',
        xlim=(-2, 12),
        ylim=(-2, 12))
ax1.legend()

# After normalization (gamma=1, beta=0)
sns.scatterplot(x=x_norm[:, 0], y=x_norm[:, 1], ax=ax2, color='crimson', alpha=0.7)
ax2.scatter(0, 0, color='blue', marker='*', s=200, label='Mean (0,0)')
ax2.axhline(y=0, color='k', linestyle='--', alpha=0.3)
ax2.axvline(x=0, color='k', linestyle='--', alpha=0.3)
ax2.set(title='After Normalization (γ=1, β=0)',
        xlabel='Normalized Feature 1',
        ylabel='Normalized Feature 2',
        xlim=(-2, 12),
        ylim=(-2, 12))
ax2.legend()

# After scaling and shifting (gamma=2, beta=1)
sns.scatterplot(x=x_scaled[:, 0], y=x_scaled[:, 1], ax=ax3, color='green', alpha=0.7)
ax3.scatter(1, 1, color='purple', marker='*', s=200, label='New Mean')
ax3.axhline(y=1, color='k', linestyle='--', alpha=0.3)
ax3.axvline(x=1, color='k', linestyle='--', alpha=0.3)
ax3.set(title='After Scale & Shift (γ=2, β=1)',
        xlabel='Scaled Feature 1',
        ylabel='Scaled Feature 2',
        xlim=(-2, 12),
        ylim=(-2, 12))
ax3.legend()

plt.tight_layout()
plt.show()

# Print statistics
print("\nOriginal Data Statistics:")
print(f"Mean: {mean}")
print(f"Variance: {x.var(axis=0)}")

print("\nNormalized Data Statistics (γ=1, β=0):")
print(f"Mean: {x_norm.mean(axis=0)}")
print(f"Variance: {x_norm.var(axis=0)}")

print("\nScaled Data Statistics (γ=2, β=1):")
print(f"Mean: {x_scaled.mean(axis=0)}")
print(f"Variance: {x_scaled.var(axis=0)}")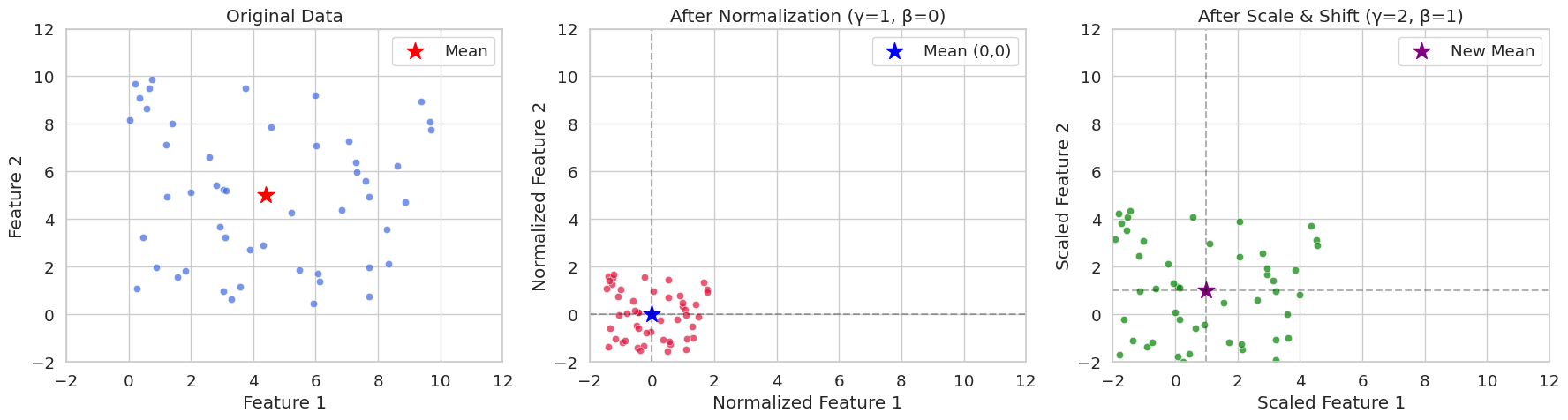

Original Data Statistics:
Mean: [4.40716778 4.99644709]
Variance: [8.89458134 8.45478364]

Normalized Data Statistics (γ=1, β=0):
Mean: [-2.70894418e-16 -3.59712260e-16]
Variance: [0.99999888 0.99999882]

Scaled Data Statistics (γ=2, β=1):
Mean: [1. 1.]
Variance: [3.9999955  3.99999527]

In seed(42) kann man häufig die zufällige Initialisierung auf 42 festlegen sehen. Dies ist eine programmiererische Praxis, und es könnte auch eine andere Zahl sein. Die 42 ist die Zahl aus Douglas Adams’ Roman “Sternenfahrts-Handbuch für galaktische Hitchhiker”, wo sie als die “Antwort auf das Leben, das Universum und alles” erwähnt wird. Deshalb wird sie von Programmierern oft in Beispielcodes u.ä. als Konvention verwendet.

6.4.2 Implementierung von Batch-Normalisierung in PyTorch

In PyTorch wird die Implementierung üblicherweise durch das Einfügen einer Batch-Normalisierungsschicht in den neuronalen Netzwerkschichten durchgeführt. Hier ist ein Beispiel dafür.

import torch.nn as nn

class SimpleNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.network = nn.Sequential(
            nn.Linear(784, 256),
            nn.BatchNorm1d(256),  # 배치 정규화 층
            nn.ReLU(),
            nn.Linear(256, 10)
        )
    
    def forward(self, x):
        return self.network(x)

Die Implementierung der Batch-Normalisierung in PyTorch kann auf Basis des Original-Quellcodes wie folgt vereinfacht werden. Wie im vorherigen Kapitel, wurde dies zur Vereinfachung und Lernzwecken implementiert.

import torch
import torch.nn as nn

class BatchNorm1d(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super().__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum

        # Trainable parameters
        self.gamma = nn.Parameter(torch.ones(num_features))  # scale
        self.beta = nn.Parameter(torch.zeros(num_features))  # shift

        # Running statistics to be tracked
        self.register_buffer('running_mean', torch.zeros(num_features))
        self.register_buffer('running_var', torch.ones(num_features))

    def forward(self, x):
        if self.training:
            # Calculate mini-batch statistics
            batch_mean = x.mean(dim=0)  # Mean per channel
            batch_var = x.var(dim=0, unbiased=False)  # Variance per channel

            # Update running statistics (important)
            self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * batch_mean
            self.running_var = (1 - self.momentum) * self.running_var + self.momentum * batch_var

            # Normalize
            x_norm = (x - batch_mean) / torch.sqrt(batch_var + self.eps)

        else:
            # During inference, use the stored statistics
            x_norm = (x - self.running_mean) / torch.sqrt(self.running_var + self.eps)

        # Apply scale and shift
        return self.gamma * x_norm + self.beta

Der wichtigste Unterschied zur grundlegenden Implementierung besteht im Update von Statistiken während der Ausführung. Während des Trainings werden die Statistiken (Mittelwert und Varianz) der Minibatches aufgehoben, um letztendlich den Gesamtmittelwert und die Gesamtvarianz zu ermitteln. Dies wird durch das Verfolgen der Bewegung mit einem exponentiellen gleitenden Mittelwert (Exponential Moving Average), das einen Momentum (Standardwert 0.1) verwendet, erreicht. Die während des Trainings gewonnenen Mittelwerte und Varianzen werden dann bei der Inferenz verwendet, um eine genaue Varianz und Abweichung für die Inferenzdaten anzuwenden und so Konsistenz zwischen Training und Inferenz zu garantieren.

Natürlich ist diese Implementierung stark vereinfacht für Lernzwecke. Der verwendete Code befindet sich unter (https://github.com/pytorch/pytorch/blob/main/torch/nn/modules/batchnorm.py). Die tatsächliche Implementierung von BatchNorm1d ist viel komplexer, da Frameworks wie PyTorch und TensorFlow neben der grundlegenden Logik auch CUDA-Optimierungen, Gradient-Optimierungen, verschiedene Einstellungsverarbeitungen und Integrationen mit C/C++ umfassen.

Klicken Sie hier, um den Inhalt anzuzeigen (Deep Dive: Herleitung der Formeln für Batch-Normalisierung und detaillierte Analyse des Backpropagation-Prozesses)

Herleitung der Formeln und detaillierte Analyse des Backpropagation-Prozesses für Batch Normalization

Batch Normalization (BN) hat seit seinem Vorschlag durch Ioffe & Szegedy im Jahr 2015 eine zentrale Technik im Training von Deep-Learning-Modellen geworden. BN normalisiert die Eingaben jeder Schicht, um das Lernverhalten zu beschleunigen, Gradientenverschwinden/-explosion zu mildern und einen gewissen Regulierungseffekt zu bieten. In diesem Tiefgang werden wir den Forward-Pass und Backpropagation-Prozess von BN detailliert untersuchen und dessen Effekte mathematisch analysieren.

Herleitung der Formeln für den Forward-Pass bei Batch Normalization

Batch Normalization wird in Mini-Batch-Einheiten durchgeführt. Wenn die Größe des Mini-Batches \(B\) und die Dimension der Merkmale (features) \(D\) ist, kann die Eingabedatenmatrix \(\mathbf{X}\) als \(B \times D\) Matrix dargestellt werden. BN wird für jede Merkmalsdimension unabhängig durchgeführt; daher betrachten wir in dieser Erklärung nur die Berechnungen für eine einzelne Merkmalsdimension.

1. Berechnung des Mini-Batch-Mittels:

   \(\mu_B = \frac{1}{B} \sum_{i=1}^{B} x_i\)

   Hierbei steht \(x_i\) für den Wert der entsprechenden Merkmalen des \(i\)-ten Samples im Mini-Batch.

2. Berechnung der Mini-Batch-Varianz:

   \(\sigma_B^2 = \frac{1}{B} \sum_{i=1}^{B} (x_i - \mu_B)^2\)

3. Normalisierung:

   \(\hat{x_i} = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\)

   Hierbei ist \(\epsilon\) eine kleine Konstante, die verhindert, dass der Nenner null wird.

4. Skalierung und Verschiebung (Scale and Shift):

   \(y_i = \gamma \hat{x_i} + \beta\)

   Hier sind \(\gamma\) und \(\beta\) lernbare Parameter, die für Skalierung und Verschiebung zuständig sind. Diese Parameter dienen dazu, die Darstellungsfähigkeit der normalisierten Daten wiederherzustellen.

Herleitung der Formeln für den Backpropagation-Prozess bei Batch Normalization - inklusive Berechnungsgraphen

Die Backpropagation bei Batch Normalization besteht darin, die Gradienten der Verlustfunktion (loss function) nach jedem Parameter mithilfe der Kettenregel (chain rule) zu berechnen. Dieser Prozess kann visuell durch einen Berechnungsgraphen dargestellt werden. (Hier wird dies in vereinfachter Form als ASCII-Art gezeigt)

     x_i   -->   [-]   -->   [/]   -->   [*]   -->   [+]   -->   y_i
      |          ^          ^          ^          ^
      |          |          |          |          |
      |          |          |          |          +---> beta
      |          |          |          +---> gamma
      |          |          +---> sqrt(...) + epsilon
      |          +---> mu_B, sigma_B^2

• \(x_i\): Eingabe
• \([-]\): Subtraktion (\(x_i - \mu_B\))
• \([/]\): Division (\((x_i - \mu_B) / \sqrt{\sigma_B^2 + \epsilon}\))
• \([*]\): Multiplikation (\(\gamma \hat{x_i}\))
• \([+]\): Addition (\(\gamma \hat{x_i} + \beta\))
• \(y_i\): Ausgabe
• \(\mu_B\): Mittelwert
• \(\sigma_B^2\): Varianz
• \(\epsilon\): Kleine Zahl, um Nullteiler zu vermeiden
• \(\gamma, \beta\): Lernparameter Nun berechnen wir die Rückwärtspropagation für jeden Schritt. Sei die Verlustfunktion \(\mathcal{L}\) und es sei angenommen, dass \(\frac{\partial \mathcal{L}}{\partial y_i}\) gegeben ist.

1. Berechnung von \(\frac{\partial \mathcal{L}}{\partial \beta}\) und \(\frac{\partial \mathcal{L}}{\partial \gamma}\):

   \(\frac{\partial \mathcal{L}}{\partial \beta} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \beta} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i}\)

   \(\frac{\partial \mathcal{L}}{\partial \gamma} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \gamma} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \hat{x_i}\)

2. Berechnung von \(\frac{\partial \mathcal{L}}{\partial \hat{x_i}}\):

   \(\frac{\partial \mathcal{L}}{\partial \hat{x_i}} = \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \hat{x_i}} = \frac{\partial \mathcal{L}}{\partial y_i} \cdot \gamma\)

3. Berechnung von \(\frac{\partial \mathcal{L}}{\partial \sigma_B^2}\):

   \(\frac{\partial \mathcal{L}}{\partial \sigma_B^2} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \sigma_B^2} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot (x_i - \mu_B) \cdot (-\frac{1}{2})(\sigma_B^2 + \epsilon)^{-3/2}\)

4. Berechnung von \(\frac{\partial \mathcal{L}}{\partial \mu_B}\):

   \(\frac{\partial \mathcal{L}}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \mu_B} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{\partial \sigma_B^2}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{-1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot (-2)\frac{1}{B}\sum_{i=1}^B (x_i-\mu_B)\)

   Da \(\sum_{i=1}^B (x_i - \mu_B) = 0\) gilt. \(\frac{\partial \mathcal{L}}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{-1}{\sqrt{\sigma_B^2 + \epsilon}}\)

5. \(\frac{\partial \mathcal{L}}{\partial x_i}\) Berechnung:

   \(\frac{\partial \mathcal{L}}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial x_i} + \frac{\partial \mathcal{L}}{\partial \mu_B} \cdot \frac{\partial \mu_B}{\partial x_i} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{\partial \sigma_B^2}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial \mathcal{L}}{\partial \mu_B} \cdot \frac{1}{B} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{2}{B}(x_i - \mu_B)\)

Erklärung, wie Batch Normalization das Problem von Gradientenverschwinden/Gradientenexplosion mildert

Batch Normalization verhindert, dass die Eingaben der Aktivierungsfunktion in extremen Werten liegen, indem es die Eingaben jeder Schicht normalisiert. Dies hilft dabei, das Problem des Gradientenverschwindens/-explodierenden Gradienten bei Aktivierungsfunktionen wie Sigmoid oder tanh zu mildern.

• Problem des Gradientenverschwindens: Wenn die Eingaben der Aktivierungsfunktion sehr groß oder sehr klein sind, nähert sich der Gradient dieser Funktion 0 an. Während des Backpropagation-Prozesses führt dies dazu, dass der Gradient verschwindet. Batch Normalization normalisiert die Eingaben auf einen Mittelwert von 0 und eine Varianz von 1, sodass die Eingaben der Aktivierungsfunktion in einem angemessenen Bereich bleiben und das Problem des Gradientenverschwindens gemildert wird.

• Problem der explodierenden Gradienten: Wenn die Eingaben der Aktivierungsfunktion sehr groß sind, kann der Gradient extrem groß werden. Batch Normalization begrenzt den Bereich der Eingaben, wodurch auch das Problem der explodierenden Gradienten gemildert wird.

Berechnung und Nutzung von laufendem Mittel (running mean, running variance) in Batch Normalization während der Inferenz

Während des Trainings berechnet Batch Normalization die Mittelwerte und Varianzen auf Mini-Batch-Ebene. Bei der Inferenz sind jedoch Schätzungen für den Mittelwert und die Varianz über das gesamte Trainingsdatensatz erforderlich. Dafür berechnet Batch Normalization während des Trainingsprozesses laufendes Mittel (running mean) und laufende Varianz (running variance).

• Berechnung des laufenden Mittels:

  \(\text{running\_mean} = (1 - \text{momentum}) \times \text{running\_mean} + \text{momentum} \times \mu_B\)

• Berechnung der laufenden Varianz:

  \(\text{running\_var} = (1 - \text{momentum}) \times \text{running\_var} + \text{momentum} \times \sigma_B^2\)

Hierbei ist momentum ein Hyperparameter, der typischerweise auf 0.1 oder 0.01 gesetzt wird.

Während der Inferenz werden die während des Trainingsprozesses berechneten running_mean und running_var verwendet, um die Eingaben zu normalisieren.

Vergleich von Batch Normalization mit anderen Normalisierungstechniken (Layer Normalization, Instance Normalization, Group Normalization)

• Batch Normalization (BN): Verwendet Statistiken zwischen den Samples innerhalb eines Minibatches. Es ist von der Batchgröße beeinflusst und schwer anwendbar auf RNNs.

• Layer Normalization (LN): Verwendet Statistiken über die Merkmalsdimensionen innerhalb jedes einzelnen Samples. Es ist nicht von der Batchgröße beeinflusst und leicht anwendbar auf RNNs.

• Instance Normalization (IN): Berechnet Statistiken unabhängig für jedes Sample und jeden Kanal. Wird hauptsächlich in Bildgenerierungsaufgaben wie Style Transfer verwendet.

• Group Normalization (GN): Teilt die Kanäle in Gruppen auf und berechnet Statistiken innerhalb jeder Gruppe. Es kann als Alternative zu BN verwendet werden, wenn die Batchgröße klein ist.

Jede Normalisierungstechnik hat Vor- und Nachteile in verschiedenen Situationen, daher muss je nach Problemeigenschaften und Modellarchitektur die geeignete Technik ausgewählt werden.

6.4.3 Anwendung bei statistischer Nachverfolgung und Inferenz

6.5 Optimierung von Hyperparametern

Die Optimierung von Hyperparametern hat einen sehr wichtigen Einfluss auf die Modellleistung. Ihre Bedeutung wurde bereits in den 1990er Jahren bekannt. In der zweiten Hälfte der 1990er Jahre wurde festgestellt, dass bei Support Vector Machines (SVM) gleiche Modelle je nach Parameter des Kernfunktion (C, gamma usw.) eine entscheidende Rolle bei der Leistung spielen. Um die Mitte der 2010er Jahre konnte bewiesen werden, dass Bayesianische Optimierung bessere Ergebnisse als manuelles Tuning liefert und wurde zu einem zentralen Bestandteil automatisierten Tunings (automated tuning) wie Google AutoML (2017) entwickelt.

6.5.1 Vergleich von Optimierungsmethoden

Es gibt verschiedene Methoden, um Hyperparameter zu optimieren. Zu den bekanntesten gehören:

1. Grid Search (Gitter-Suche): Dies ist die grundlegendste Methode, bei der für jeden Hyperparameter eine Liste möglicher Werte angegeben wird und alle Kombinationen dieser Werte ausprobiert werden. Sie ist nützlich, wenn die Anzahl der Hyperparameter gering ist und das Spektrum der möglichen Werte für jeden Parameter begrenzt ist. Allerdings sind die Berechnungskosten sehr hoch, da jede Kombination getestet werden muss. Es eignet sich für einfache Modelle oder kleinere Suchräume.

2. Random Search (Zufallssuche): Diese Methode erzeugt Kombinationen durch zufällige Auswahl der Werte für jeden Hyperparameter und bewertet die Leistung des Modells auf Basis dieser Kombinationen. Wenn einige Hyperparameter einen größeren Einfluss auf die Leistung haben, kann dies effektiver sein als Gitter-Suche (Bergstra & Bengio, 2012).

3. Bayesian Optimization (Bayes’sche Optimierung): Diese Methode wählt intelligente Kombinationen von Hyperparametern auf Basis früherer Suchergebnisse und verwendet ein Wahrscheinlichkeitsmodell (in der Regel ein Gaußsches Prozess) um die nächsten zu probierenden Kombinationen auszuwählen. Die optimale Stelle wird durch Maximierung einer Erwerbsfunktion (acquisition function) bestimmt. Da sie den Suchraum für Hyperparameter effizient erkundet, kann sie mit weniger Versuchen bessere Kombinationen finden als Gitter-Suche oder Zufallssuche.

Neben diesen gibt es auch Evolutionäre Algorithmen, die auf genetischen Algorithmen basieren, und gradientenbasierte Optimierungsmethoden.

Im Folgenden wird ein Beispiel gezeigt, wie Hyperparameter eines einfachen neuronalen Netzes mit Bayes’scher Optimierung optimiert werden.

6.5.2 Optimierung mit Bayes-Opt

Bayes’sche Optimierung erhielt in den 2010er Jahren zunehmend an Bedeutung. Im Gegensatz zu Gitter-Suche oder Zufallssuche, die zufällige oder systematische Kombinationen ausprobieren, wählt Bayes’sche Optimierung intelligente Parameterkombinationen auf Basis früherer Versuche. Dies ist ein großer Vorteil.

Die Bayes’sche Optimierung besteht im Wesentlichen aus den folgenden drei Schritten:

1. Initiale Stichproben (Initialization): Ein zufälliger Satz von Hyperparameterkombinationen, wie in init_points definiert, wird verwendet, um das Modell zu trainieren und die Leistung zu bewerten.
2. Surrogate Model (Stellvertretendes Modell) erstellen: Basierend auf den bisherigen Experimenten wird ein stellvertretendes Modell (meist ein Gaußscher Prozess) erstellt, das das Verhältnis zwischen Hyperparametern und Leistung modelliert.
3. Optimierung der Erwerbsfunktion (Acquisition Function): Basierend auf dem stellvertretenden Modell wird die optimale Kombination von Hyperparametern für den nächsten Versuch ausgewählt, indem eine Erwerbsfunktion verwendet wird. Die Erwerbsfunktion findet das optimale Gleichgewicht zwischen “Erkundung (exploration)” und “Nutzung (exploitation)”, basierend auf der aktuellen Information (stellvertretendes Modell).
4. Wiederholen der Schritte 2-3.

import torch
import torch.nn as nn
import torch.optim as optim
from dldna.chapter_04.models.base import SimpleNetwork  
from dldna.chapter_04.utils.data import get_data_loaders, get_device  
from bayes_opt import BayesianOptimization
from dldna.chapter_04.experiments.model_training import train_model, eval_loop  


def train_simple_net(hidden_layers, learning_rate, batch_size, epochs):
    """Trains a SimpleNetwork model with given hyperparameters.
       Uses CIFAR100 dataset and train_model from Chapter 4.
    """
    device = get_device()  # Use the utility function to get device

    # Get data loaders for CIFAR100
    train_loader, test_loader = get_data_loaders(dataset="CIFAR100", batch_size=batch_size)

    # Instantiate the model with specified activation and hidden layers.
    # CIFAR100 images are 3x32x32, so the input size is 3*32*32 = 3072.
    model = SimpleNetwork(act_func=nn.ReLU(), input_shape=3*32*32, hidden_shape=hidden_layers, num_labels=100).to(device)

    # Optimizer: Use Adam
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)

    # Train the model using the training function from Chapter 4
    results = train_model(model, train_loader, test_loader, device, optimizer=optimizer, epochs=epochs, save_dir="./tmp/tune",
                         retrain=True) # retrain=True로 설정

    # Return the final test accuracy
    return results['test_accuracies'][-1]


def train_wrapper(learning_rate, batch_size, hidden1, hidden2):
    """Wrapper function for Bayesian optimization."""
    return train_simple_net(
        hidden_layers=[int(hidden1), int(hidden2)],
        learning_rate=learning_rate,
        batch_size=int(batch_size),
        epochs=10
    )

def optimize_hyperparameters():
    """Runs hyperparameter optimization."""
    # Set the parameter ranges to be optimized.
    pbounds = {
        "learning_rate": (1e-4, 1e-2),
        "batch_size": (64, 256),
        "hidden1": (64, 512),  # First hidden layer
        "hidden2": (32, 256)   # Second hidden layer
    }

    # Create a Bayesian optimization object.
    optimizer = BayesianOptimization(
        f=train_wrapper,
        pbounds=pbounds,
        random_state=1,
        allow_duplicate_points=True
    )

    # Run optimization
    optimizer.maximize(
        init_points=4,
        n_iter=10,
    )

    # Print the best parameters and accuracy
    print("\nBest parameters found:")
    print(f"Learning Rate: {optimizer.max['params']['learning_rate']:.6f}")
    print(f"Batch Size: {int(optimizer.max['params']['batch_size'])}")
    print(f"Hidden Layer 1: {int(optimizer.max['params']['hidden1'])}")
    print(f"Hidden Layer 2: {int(optimizer.max['params']['hidden2'])}")
    print(f"\nBest accuracy: {optimizer.max['target']:.4f}")

if __name__ == "__main__":
    print("Starting hyperparameter optimization...")
    optimize_hyperparameters()

Das folgende Beispiel führt eine Hyperparameter-Optimierung mit dem Paket BayesOpt durch. Das Trainingsziel ist das SimpleNetwork (aus Kapitel 4 definiert), und der CIFAR100-Datensatz wird verwendet. Die Funktion train_wrapper dient als Zielfunktion für BayesOpt, trainiert das Modell mit den gegebenen Hyperparametern und gibt die endgültige Testgenauigkeit zurück.

pbounds gibt das Suchintervall für jeden Hyperparameter an. Bei optimizer.maximize ist init_points die Anzahl der initialen zufälligen Suchschritte, n_iter die Anzahl der Wiederholungen der bayesianischen Optimierung. Die gesamte Anzahl der Experimente beträgt daher init_points + n_iter.

Beim Durchsuchen von Hyperparametern sind folgende Punkte zu beachten:

1. Parameterbereich: Ein zu breiter Bereich kann die Suchzeit erhöhen, ein zu enger Bereich kann das Optimum verfehlen. In der Regel wird die Lernrate in logarithmischer Skala (1e-4 ~ 1e-2) und die Anzahl der Neuronen in Potenzen von 2 angegeben.
2. Anzahl der Wiederholungen: Die gesamte Anzahl der Versuche sollte erfahrungsgemäß etwa (Anzahl der Parameter) x 20 betragen, um gute Ergebnisse zu erzielen. Im obigen Beispiel sind es 4 Parameter, daher können insgesamt 14 Versuche (init_points=4, n_iter=10) als etwas niedrig sein. Für bessere Ergebnisse kann man in Betracht ziehen, n_iter zu erhöhen.

6.5.3 Optimierung mit BoTorch

Kürzlich hat das Framework BoTorch in der Domäne der Hyperparameter-Optimierung für Deep Learning Aufmerksamkeit erhalten. BoTorch ist ein auf PyTorch basierendes Bayesianisches Optimierungsframework, das 2019 von FAIR (Facebook AI Research, heute Meta AI) entwickelt wurde. Bayes-Opt ist eine ältere, seit 2016 entwickelte Bibliothek für Bayesianische Optimierung und bietet eine intuitive und einfache Schnittstelle (API im Stil von scikit-learn), die es weit verbreitet macht.

Die Vor- und Nachteile beider Bibliotheken sind klar:

• BoTorch:
  • Vorteile: Integration mit Deep-Learning-Modellen, GPU-Beschleunigung, hohe Abtasteffizienz, eine Vielzahl von fortgeschrittenen Bayesianischen Optimierungstechniken (multi-fidelity, multi-task, Constraint-Optimierung usw.), Unterstützung von automatischer Differentiation und spezialisierte Funktionen für die Hyperparameter-Optimierung von Deep-Learning-Modellen. Es ist insbesondere für große Modelle, hochdimensionale Parameterräume und rechenintensive Experimente geeignet.
  • Nachteile: Im Vergleich zu Bayes-Opt erfordert es relativ mehr Lernzeit und kann eine komplexe Anfangskonfiguration haben.
• Bayes-Opt:
  • Vorteile: Es bietet eine einfache und intuitive API, ist einfach zu installieren und verfügt über reichhaltige Tutorials und Beispielcodes.
  • Nachteile: Im Vergleich zu BoTorch fehlen fortgeschrittene Funktionen, die Integration mit Deep-Learning-Modellen ist relativ weniger glatt. Bei großen/hochdimensionalen Problemen kann sich die Leistung verschlechtern.

Daher ist Bayes-Opt für einfache Probleme oder schnelle Prototypen geeignet, während BoTorch für komplexe Hyperparameter-Optimierungen von Deep-Learning-Modellen, große/hochdimensionale Probleme und fortgeschrittene Bayesianische Optimierungstechniken (z.B. multi-task, Constraint-Optimierung) empfohlen wird.

Um BoTorch zu verwenden, müssen im Gegensatz zu Bayes-Opt einige Kernkonzepte für die Anfangskonfiguration verstanden werden (Stellvertretermodelle, Normalisierung der Eingabedaten, Erwerbsfunktionen).

1. Stellvertreter(Surrogate) Modell:

   Ein Stellvertretermodell ist ein Modell, das die tatsächliche Zielfunktion (hier die Validierungspräzision des Deep-Learning-Modells) annähert. Üblicherweise werden Gaußprozesse (GP) verwendet. GP werden anstelle der rechenintensiven tatsächlichen Zielfunktion genutzt, um schnell und kostengünstig Ergebnisse vorherzusagen. BoTorch bietet die folgenden GP-Modelle:

   • SingleTaskGP: Das grundlegende Gaußprozessmodell, das für Einzelzieloptimierungsprobleme geeignet ist und effektiv bei bis zu 1000 Datenpunkten arbeitet.
   • MultiTaskGP: Für die gleichzeitige Optimierung mehrerer Zielfunktionen (multi-objective optimization) verwendet. Zum Beispiel kann sowohl die Präzision als auch die Inferenzzeit des Modells optimiert werden.
   • SAASBO (Sparsity-Aware Adaptive Subspace Bayesian Optimization): Ein Modell, das auf hochdimensionalen Parameterräumen spezialisiert ist. Es geht davon aus, dass in hochdimensionalen Räumen Sparsität existiert und führt eine effiziente Exploration durch.

2. Normalisierung der Eingabedaten:

   Da Gaußprozesse empfindlich gegenüber der Skalierung von Daten sind, ist die Normalisierung der Eingabedaten (Hyperparameter) wichtig. Üblicherweise werden alle Hyperparameter in den Bereich [0, 1] transformiert. BoTorch bietet die Transformationen Normalize und Standardize.

3. Erwerbsfunktion (Acquisition Function): Erwerbfunktionen basieren auf dem Surrogatmodell (GP) und werden verwendet, um die nächste Kombination von Hyperparametern zu bestimmen, die experimentiert werden soll. Erwerbfunktionen spielen die Rolle, das Gleichgewicht zwischen “Exploration” und “Exploitation” aufrechtzuerhalten. BoTorch bietet eine Vielzahl von Erwerbfunktionen an.

• ExpectedImprovement (EI): Eine der am häufigsten verwendeten Erwerbfunktionen. Sie berücksichtigt die Wahrscheinlichkeit, ein besseres Ergebnis als das aktuelle Optimum zu erzielen, und den Grad dieser Verbesserung.
• LogExpectedImprovement (LogEI): Die logarithmische Transformation von EI. Numerisch stabiler und sensibler gegenüber kleinen Veränderungen.
• UpperConfidenceBound (UCB): Eine Erwerbfunktion, die stärker auf Exploration fokussiert ist. Sie erforscht Bereiche mit hoher Unsicherheit aktivierter.
• ProbabilityOfImprovement (PI): Zeigt die Wahrscheinlichkeit an, das aktuelle Optimum zu verbessern.
• qExpectedImprovement (qEI): Auch als q-batch EI bekannt und für parallele Optimierung verwendet. Wählt mehrere Kandidaten auf einmal aus.
• qNoisyExpectedImprovement (qNEI): q-batch Noisy EI, verwendet in Umgebungen mit Rauschen.

Der gesamte Code befindet sich in package/botorch_optimization.py. Er kann direkt von der Kommandozeile ausgeführt werden. Der vollständige Code enthält detaillierte Kommentare, daher werde ich hier nur die wichtigsten Teile jedes Codes erläutern.

def __init__(self, max_trials: int = 80, init_samples: int = 10):
    self.param_bounds = torch.tensor([
        [1e-4, 64.0, 32.0, 32.0],      # 최소값
        [1e-2, 256.0, 512.0, 512.0]    # 최대값
    ], dtype=torch.float64)

In der Initialisierungsteil werden die Minimal- und Maximalwerte für jeden Hyperparameter festgelegt. max_trials ist die Gesamtzahl der Versuche, init_samples ist die Anzahl der anfänglichen zufälligen Experimente (entspricht init_points in Bayes-Opt). init_samples wird üblicherweise auf 2-3-fach der Anzahl der Parameter gesetzt. Im obigen Beispiel gibt es 4 Hyperparameter, daher sind etwa 8-12 geeignet. Der Grund für die Verwendung von torch.float64 ist die numerische Stabilität. Bei der Bayesschen Optimierung, insbesondere beim Gaußschen Prozess, wird bei der Berechnung der Kernmatrix die Cholesky-Zerlegung verwendet, wobei float32 aufgrund von Genauigkeitsproblemen zu Fehlern führen kann.

def tune(self):
    # 가우시안 프로세스 모델 학습
    model = SingleTaskGP(configs, accuracies)
    mll = ExactMarginalLogLikelihood(model.likelihood, model)
    fit_gpytorch_mll(mll)

Gaußsche Prozesse basierte Surrogatmodelle verwenden SingleTaskGP. ExactMarginalLogLikelihood ist die Verlustfunktion zum Trainieren des Modells und fit_gpytorch_mll trainiert das Modell mit dieser Verlustfunktion.

acq_func = LogExpectedImprovement(
    model, 
    best_f=accuracies.max().item()
)

Die Erwerbfunktion LogExpectedImprovement wird verwendet. Da der Logarithmus angewendet wird, ist sie numerisch stabil und reagiert empfindlich auf kleine Änderungen.

candidate, _ = optimize_acqf(                                   # 획득 함수 최적화로 다음 실험할 파라미터 선택
    acq_func, bounds=bounds,                                    # 획득 함수와 파라미터 범위 지정
    q=1,                                                        # 한 번에 하나의 설정만 선택
    num_restarts=10,                                            # 최적화 재시작 횟수
    raw_samples=512                                             # 초기 샘플링 수
)

optimize_acqf Funktion optimiert die Erwerbsfunktion, um die nächste Kombination von Hyperparametern (Kandidat) für das Experiment auszuwählen.

• q=1: Wählt nur einen Kandidaten auf einmal (keine q-Batch-Optimierung).
• num_restarts=10: Führt die Optimierung in jedem Schritt 10-mal mit verschiedenen Startpunkten durch, um das Fallen in lokale Optima zu vermeiden.
• raw_samples=512: Extrahiert 512 Stichproben aus dem Gaußschen Prozess, um den Wert der Erwerbsfunktion zu schätzen.

num_restarts und raw_samples haben einen großen Einfluss auf das Trade-off zwischen Exploration und Exploitation in der Bayesianischen Optimierung. num_restarts bestimmt die Gründlichkeit der Optimierung, während raw_samples die Genauigkeit der Erwerbsfunktionsschätzung beeinflusst. Je höher diese Werte sind, desto höher sind die Rechenkosten, aber auch die Wahrscheinlichkeit, bessere Ergebnisse zu erzielen. Allgemein können folgende Werte verwendet werden:

• Schnelle Ausführung: num_restarts=5, raw_samples=256
• Ausgewogen: num_restarts=10, raw_samples=512
• Genauigkeit fokussiert: num_restarts=20, raw_samples=1024

from dldna.chapter_06.botorch_optimizer import run_botorch_optimization

run_botorch_optimization(max_trials=80, init_samples=5)

Ergebnis Datensatz : FashionMNIST Epochen : 20 Initiale Experimente : 5 Mal Wiederholte Experimente : 80 Mal

Optimale Parameter	Bayes-Opt	Botorch
Lernrate	6e-4	1e-4
Batch-Größe	173	158
hid 1	426	512
hid 2	197	512
Genauigkeit	0.7837	0.8057

Es ist eine einfache Vergleich, aber die Genauigkeit von BoTorch ist höher. Bei einfachen Optimierungssuchen wird Bayes-Opt empfohlen, bei fortgeschrittenen Suchen jedoch BoTorch.

6.6 Gaußsche Prozesse

Herausforderung: Wie kann die Vorhersageunsicherheit eines Modells quantifiziert werden und dazu verwendet werden, aktiv zu lernen?

Frust des Forschers: Traditionelle Deep-Learning-Modelle liefern Vorhersagergebnisse als Punktschätzungen (point estimates), aber in realen Anwendungen ist die Kenntnis der Unsicherheit einer Vorhersage von großer Bedeutung. Zum Beispiel muss ein autonomes Fahrzeug beim Vorhersagen der nächsten Position eines Fußgängers wissen, wie unsicher diese Vorhersage ist, um sicher zu fahren. Gaußsche Prozesse sind leistungsstarke Werkzeuge zur Quantifizierung der Vorhersageunsicherheit auf Basis der bayesianischen Wahrscheinlichkeitstheorie, haben aber den Nachteil, dass sie rechenaufwändig sind und schwer an große Datenmengen anzupassen.

Gaußsche Prozesse (Gaussian Process, GP) sind zentrale Modelle im Bayesianischen Maschinellen Lernen, die unsichere Vorhersagen (uncertainty-aware prediction) bereitstellen. Wir haben bereits kurz auf die Verwendung von Gaußschen Prozessen als Surrogatmodelle in der bayesianischen Optimierung eingegangen; hier wollen wir uns detaillierter mit den grundlegenden Prinzipien und der Bedeutung von Gaußschen Prozessen selbst befassen.

Ein GP wird als “Wahrscheinlichkeitsverteilung über Mengen von Funktionswerten” definiert. Im Gegensatz zu deterministischen Funktionen wie \(y = f(x)\), die eine einzelne Ausgabe für einen gegebenen Eingang liefern, vorhersagt ein GP nicht eine einzelne Ausgabe für eine gegebene Eingabe \(x\), sondern eine Verteilung möglicher Ausgaben. Zum Beispiel anstatt festzulegen, “die höchste Temperatur morgen wird 25 Grad sein”, kann man sagen, “es gibt eine 95%-ige Wahrscheinlichkeit, dass die höchste Temperatur morgen zwischen 23 und 27 Grad liegt”. Wenn man Fahrrad fährt, um nach Hause zu kommen, ist der grobe Weg bereits festgelegt, aber jedes Mal wird der tatsächliche Weg unterschiedlich sein. In solchen Fällen sind unsichere Vorhersagen erforderlich.

Die mathematischen Werkzeuge zur Behandlung unsicherer Vorhersagen basieren auf dem von dem 19. Jahrhundert Mathematiker Gauß vorgeschlagenen Normalverteilung (Gaußsche Verteilung). Darauf basierend entwickelten sich in den 1940er Jahren die GP. Es war die Zeit des Zweiten Weltkrieges, als Wissenschaftler mit unsicheren Daten umgehen mussten wie Radar-Signalverarbeitung, Entschlüsselung und Wetterdaten-Verarbeitung. Ein berühmtes Beispiel ist das von Norbert Wiener entwickelte Prädiktionsfilter für Flugabwehrgeschütze. In der Zeitreihenanalyse arbeitete Harald Cramér, in der Wahrscheinlichkeitstheorie Andrey Kolmogorov an den mathematischen Grundlagen der GP. 1951 prägte Daniel Krige mit der Anwendung von GP zur Vorhersage von Erzlagerstätten die praktische Anwendung. In den 1970er Jahren wurden durch Statistiker räumliche Anwendungen, Designs für Computerexperimente und Bayesianische Optimierung im maschinellen Lernen systematisiert. Heute spielen sie in fast allen Bereichen, die mit Unsicherheiten umgehen müssen, wie Künstlicher Intelligenz, Robotik und Klimavorhersage eine zentrale Rolle. Insbesondere in der Tiefen Lernung sind tief gehende Kernel-GP durch Meta-Lernen hervorragend aufgetreten, insbesondere in Bereichen wie der Vorhersage molekularer Eigenschaften.

Heute werden Gaußsche Prozesse in verschiedenen Bereichen eingesetzt, darunter Künstliche Intelligenz, Robotik und Klimamodellierung. Insbesondere in der Tiefen Lernung zeigen sie durch Meta-Lernen und tiefgehende Kernel-GP in Bereichen wie der Vorhersage molekularer Eigenschaften hervorragende Leistungen.

Klicken Sie hier, um den Inhalt anzuzeigen (Tiefgang: Mathematische Grundlagen von Gaußschen Prozessen und ihre Anwendung im Maschinellen Lernen)

Mathematische Grundlagen des Gaussian Processes und Anwendungen im Maschinellen Lernen

Der Gaussian Process (GP) ist ein stochastisches Modell, das auf Kernmethoden (kernel methods) basiert und in Regressions- und Klassifikationsproblemen weit verbreitet ist. GPs definieren eine Verteilung über Funktionen selbst, was es ermöglicht, die Unsicherheit von Vorhersagen zu quantifizieren. In diesem Deep Dive untersuchen wir detailliert die mathematischen Grundlagen des Gaussian Processes, beginnend mit der multivariaten Normalverteilung bis hin zur Perspektive stochastischer Prozesse und erforschen verschiedene Anwendungen im maschinellen Lernen.

1. Multivariate Normalverteilung (Multivariate Normal Distribution)

Der erste Schritt zum Verstehen von Gaussian Processes ist das Verständnis der multivariaten Normalverteilung. Ein \(d\)-dimensionaler Zufallsvektor \(\mathbf{x} = (x_1, x_2, ..., x_d)^T\), der multivariat normalverteilt ist, hat die folgende Wahrscheinlichkeitsdichtefunktion (probability density function).

\(p(\mathbf{x}) = \frac{1}{(2\pi)^{d/2}|\mathbf{\Sigma}|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)\)

Dabei ist \(\boldsymbol{\mu} \in \mathbb{R}^d\) der Mittelwertsvektor und \(\mathbf{\Sigma} \in \mathbb{R}^{d \times d}\) die Kovarianzmatrix (covariance matrix). Die Kovarianzmatrix muss positiv definit sein.

Kernmerkmale:

• Lineare Transformation: Eine lineare Transformation einer multivariat normalverteilten Zufallsvariablen ist ebenfalls multivariat normalverteilt. Das heißt, wenn \(\mathbf{x} \sim \mathcal{N}(\boldsymbol{\mu}, \mathbf{\Sigma})\) und \(\mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{b}\), dann ist \(\mathbf{y} \sim \mathcal{N}(\mathbf{A}\boldsymbol{\mu} + \mathbf{b}, \mathbf{A}\mathbf{\Sigma}\mathbf{A}^T)\).

• Bedingte Verteilung (Conditional Distribution): Die bedingte Verteilung einer multivariaten Normalverteilung ist ebenfalls normalverteilt. Wenn \(\mathbf{x}\) in \(\mathbf{x} = (\mathbf{x}_1, \mathbf{x}_2)^T\) unterteilt wird und der Mittelwert und die Kovarianzmatrix wie folgt unterteilt sind:

  \(\boldsymbol{\mu} = \begin{pmatrix} \boldsymbol{\mu}_1 \\ \boldsymbol{\mu}_2 \end{pmatrix}, \quad \mathbf{\Sigma} = \begin{pmatrix} \mathbf{\Sigma}_{11} & \mathbf{\Sigma}_{12} \\ \mathbf{\Sigma}_{21} & \mathbf{\Sigma}_{22} \end{pmatrix}\)

  dann ist die bedingte Verteilung von \(\mathbf{x}_2\) gegeben \(\mathbf{x}_1\) wie folgt:

  \(p(\mathbf{x}_2 | \mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu}_{2|1}, \mathbf{\Sigma}_{2|1})\)

  \(\boldsymbol{\mu}_{2|1} = \boldsymbol{\mu}_2 + \mathbf{\Sigma}_{21}\mathbf{\Sigma}_{11}^{-1}(\mathbf{x}_1 - \boldsymbol{\mu}_1)\) \(\mathbf{\Sigma}_{2|1} = \mathbf{\Sigma}_{22} - \mathbf{\Sigma}_{21}\mathbf{\Sigma}_{11}^{-1}\mathbf{\Sigma}_{12}\)

• Randverteilung (Marginal Distribution): Die Randverteilungen einer multivariaten Normalverteilung sind ebenfalls normalverteilt. In der obigen Zerlegung ist die Randverteilung von \(\mathbf{x}_1\) wie folgt. \(p(\mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu_1}, \mathbf{\Sigma}_{11})\)

2. Definition und stochastische Prozess-Sichtweise des Gaußschen Prozesses

Ein Gaußscher Prozess ist eine Wahrscheinlichkeitsverteilung über Funktionen. Das bedeutet, dass ein gegebener Funktion \(f(x)\) einem Gaußschen Prozess folgt, wenn der Vektor der Funktionswerte \((f(x_1), f(x_2), ..., f(x_n))^T\) für jede endliche Menge von Eingabepunkten \(\{x_1, x_2, ..., x_n\}\) einer multivariaten Normalverteilung folgt.

Definition: Ein Gaußscher Prozess ist durch eine Mittelfunktion (mean function) \(m(x)\) und eine Kovarianzfunktion (covariance function oder Kernel-Funktion) \(k(x, x')\) definiert.

\(f(x) \sim \mathcal{GP}(m(x), k(x, x'))\)

• Mittelfunktion: \(m(x) = \mathbb{E}[f(x)]\)
• Kovarianzfunktion: \(k(x, x') = \mathbb{E}[(f(x) - m(x))(f(x') - m(x'))]\)

Sichtweise als stochastischer Prozess (Stochastic Process): Ein Gaußscher Prozess ist eine Art von stochastischem Prozess, bei dem jeder Element eines Index-Satzes (hier der Eingaberaum) einer Zufallsvariable zugeordnet wird. Im Falle eines Gaußschen Prozesses bilden diese Zufallsvariablen eine gemeinsame Normalverteilung.

3. Rolle und Einführung verschiedener Kernel-Funktionen

Die Kernel-Funktion ist ein wesentlicher Bestandteil des Gaußschen Prozesses. Sie repräsentiert die Ähnlichkeit zwischen zwei Eingaben \(x\) und \(x'\) und bestimmt die Eigenschaften des Gaußschen Prozesses.

Wichtige Rollen:

• Kovarianzdefinition: Die Kernel-Funktion definiert die Kovarianz zwischen Funktionswerten. D.h., \(k(x, x')\) ist die Kovarianz zwischen \(f(x)\) und \(f(x')\).
• Bestimmung der Funktionsschwelligkeit (Smoothness): Die Kernel-Funktion bestimmt die Schwelligkeit der erzeugten Funktionen. Zum Beispiel erzeugt der RBF-Kernel glatte, beliebig oft differenzierbare Funktionen, während der Matérn-Kernel die Differenzierbarkeit regeln kann.
• Positive Definitheit (Positive Definiteness): Um eine gültige Kovarianzfunktion zu sein, muss die Kernel-Funktion positiv definit sein. Das bedeutet, dass die aus beliebigen Eingabepunkten generierte Kernel-Matrix (Covariance Matrix) eine positive definit Matrix ist.

Verschiedene Kernel-Funktionen:

• RBF (Radial Basis Function) Kernel (oder Squared Exponential-Kernel):

  \(k(x, x') = \sigma^2 \exp\left(-\frac{\|x - x'\|^2}{2l^2}\right)\)

  • \(\sigma^2\): Varianz
  • \(l\): Längenskala (length scale)
  • Erzeugt sehr glatte Funktionen.

• Matérn-Kernel:

  \(k(x, x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)}\left(\sqrt{2\nu}\frac{\|x - x'\|}{l}\right)^\nu K_\nu\left(\sqrt{2\nu}\frac{\|x - x'\|}{l}\right)\)

• \(\nu\): Weichheitsparameter (smoothness parameter)

• \(K_\nu\): Modifizierte Bessel-Funktion (modified Bessel function)

• \(\nu = 1/2, 3/2, 5/2\) werden häufig als Halbzahlen (half-integer) verwendet.

• Je größer \(\nu\), desto ähnlicher wird der RBF-Kernel.

• Periodischer (Periodic) Kernel:

  \(k(x, x') = \sigma^2 \exp\left(-\frac{2\sin^2(\pi|x-x'|/p)}{l^2}\right)\)

  • \(p\) : Periode

• Linearer (Linear) Kernel:

  \(k(x,x') = \sigma_b^2 + \sigma_v^2(x - c)(x' -c)\)

4. Lösung von Regressions- und Klassifikationsproblemen mit Gaußschen Prozessen

Regression:

Die Gaußsche-Prozess-Regression (Gaussian Process Regression) befasst sich damit, für eine neue Eingabe \(\mathbf{x}_*\) die Ausgabe \(f(\mathbf{x}_*)\) basierend auf gegebenen Trainingsdaten \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^n\) vorherzusagen. Die Vorhersageverteilung (predictive distribution) wird durch Kombination der a-priori-Verteilung (prior distribution) des Gaußschen Prozesses mit den Trainingsdaten berechnet.

• A-Priori-Verteilung: \(f(\mathbf{x}) \sim \mathcal{GP}(0, k(\mathbf{x}, \mathbf{x}'))\) (für Vereinfachung wird die Mittelfunktion als 0 angenommen)
• Trainingsdaten: \(\mathbf{y} = (y_1, y_2, ..., y_n)^T\)
• Kernmatrix: \(\mathbf{K} = k(\mathbf{X}, \mathbf{X})\), wobei \(\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_n]\)
• Vorhersageverteilung: \(p(f(\mathbf{x}_*) | \mathbf{y}, \mathbf{X}, \mathbf{x}_*) = \mathcal{N}(\mu_*, \sigma_*^2)\)
  • \(\mu_* = \mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{y}\)
  • \(\sigma_*^2 = k(\mathbf{x}_*, \mathbf{x}_*) - \mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{k}_*\)
  • \(\mathbf{k}_* = [k(\mathbf{x}_*, \mathbf{x}_1), k(\mathbf{x}_*, \mathbf{x}_2), ..., k(\mathbf{x}_*, \mathbf{x}_n)]^T\)

Klassifikation:

Die Gaußsche-Prozess-Klassifikation (Gaussian Process Classification) modelliert die latente Funktion \(f(\mathbf{x})\) als Gaußscher Prozess und definiert die Klassifikationswahrscheinlichkeiten durch diese latente Funktion. Zum Beispiel wird in binären Klassifikationsproblemen die latente-Funktionswerte über eine Logit- oder Probitfunktion in Wahrscheinlichkeiten umgewandelt.

• Latente Funktion: \(f(\mathbf{x}) \sim \mathcal{GP}(0, k(\mathbf{x}, \mathbf{x}'))\)
• Binäre Klassifikation: \(p(y = 1 | f(\mathbf{x})) = \sigma(f(\mathbf{x}))\) (wobei \(\sigma\) die Logitfunktion ist)

Da in Klassifikationsproblemen die a-posteriori-Verteilung nicht in geschlossener Form vorliegt, werden approximative Inferenzmethoden wie die Laplace-Approximation oder variationelle Inferenz verwendet. ### 5. Vor- und Nachteile von Gaußschen Prozessen sowie Vergleich mit tiefem Lernen

Vorteile:

• Quantifizierung der Unsicherheit: Bietet die Unsicherheit der Vorhersage in Form der vorhergesagten Varianz (predictive variance).
• Daten-effizient: Kann auch bei relativ kleinen Datenmengen gute Leistungen erzielen.
• Flexibilität bei Kernel-Wahl: Verschiedene Kernelfunktionen können verwendet werden, um Modelle anzupassen, die den Eigenschaften des Problems entsprechen.
• Bayessche Interpretation: Lässt sich natürlicherweise im bayesianischen Rahmen interpretieren.

Nachteile:

• Berechnungskomplexität: Hat eine Berechnungskomplexität von \(O(n^3)\) in Bezug auf die Größe der Trainingsdaten \(n\). (aufgrund der Invertierung)
• Modellauswahl: Die Auswahl geeigneter Kernelfunktionen und Hyperparameter ist wichtig und kann schwierig sein.
• Hochdimensionale Eingaben: In hochdimensionalen Eingaberaum kann die Leistung nachlassen.

Vergleich mit tiefem Lernen:

• Datenbedarf: Tiefes Lernen erfordert im Allgemeinen viel mehr Daten als Gaußsche Prozesse.
• Berechnungsaufwand: Tiefes Lernen erfordert bei der Training einen hohen Berechnungsaufwand, die Inferenz ist jedoch relativ schnell. Gaußsche Prozesse sind (bei wenigen Daten) beim Training schneller, aber bei der Inferenz steigt der Berechnungsaufwand mit der Datenmenge.
• Unsicherheit: Tiefes Lernen bietet im Allgemeinen keine Unsicherheit über die Vorhersage. (Es gibt jedoch Ausnahmen wie bayesianisches tiefes Lernen (Bayesian deep learning).)
• Ausdrucksstärke: Tiefes Lernen kann sehr komplexe Funktionen darstellen, während Gaußsche Prozesse durch die Kernelfunktion in ihrer Ausdrucksstärke begrenzt sind.
• Interpretierbarkeit: Gaußsche Prozesse ermöglichen es, Annahmen des Modells über Kernel-Funktionen zu spezifizieren und Unsicherheiten der Vorhersageergebnisse zu quantifizieren.

In jüngster Zeit werden auch Modelle erforscht, die tiefes Lernen und Gaußsche Prozesse kombinieren (z. B. Deep Kernel Learning).

6.6.1 Mathematische Grundlagen der Unsicherheitsbehandlung

Im Allgemeinen denken wir an eine Funktion als eine einzelne Linie, aber ein Gaußscher Prozess betrachtet sie als “Menge möglicher Linien”. Mathematisch ausgedrückt ist es wie folgt.

\(f(t) \sim \mathcal{GP}(m(t), k(t,t'))\)

Wenn wir das Beispiel eines Fahrradstandorts nehmen, dann stellt \(m(t)\) die Mittelfunktion dar und “vorausgesagt wird, dass der Pfad ungefähr so verlaufen wird”. \(k(t,t')\) ist die Kovarianzfunktion (oder Kernel), welche angibt, “wie stark sich Standorte zu verschiedenen Zeitpunkten voneinander abhängen?”. Es gibt mehrere typische Kernels. Ein häufig verwendeter Kernel ist der RBF (Radial Basis Function).

\(k(t,t') = \sigma^2 \exp\left(-\frac{(t-t')^2}{2l^2}\right)\)

Diese Formel ist sehr intuitiv. Je näher die beiden Zeitpunkte \(t\) und \(t'\) beieinander liegen, desto größer ist der Wert, und je weiter sie auseinanderliegen, desto kleiner ist der Wert. Es ähnelt “wenn man den aktuellen Standort kennt, kann man den Standort in ein paar Minuten etwa vorhersagen, aber den Standort in ferner Zukunft nicht so gut”.

Nehmen wir an, der Kernel (\(K\)) ist RBF und betrachten wir ein Beispiel. Stellen Sie sich vor, Sie betreiben einen Fahrrad-Sharing-Dienst (oder auch autonomes Fahren). Wir schätzen die gesamte Bewegungspfad eines Fahrrads basierend nur auf wenigen GPS-Datenpunkten.

Grundlegende Formel der Vorhersage

\(f_* | X, y, X_* \sim \mathcal{N}(\mu_*, \Sigma_*)\)

Diese Formel bedeutet “basierend auf unseren GPS-Aufzeichnungen (\(X\), \(y\)), folgt die Position des Fahrrads zu unbekannten Zeitpunkten (\(X_*\)) einer Normalverteilung mit Mittelwert \(\mu_*\) und Unsicherheit \(\Sigma_*\)”.

Berechnung der Standortvorhersage

\(\mu_* = K_*K^{-1}y\)

Diese Formel zeigt, wie die Position des Fahrrads vorhergesagt wird. \(K_*\) repräsentiert den ‘zeitlichen Zusammenhang’ zwischen den zu prognostizierenden Zeitpunkten und den GPS-Aufzeichnungspunkten; \(K^{-1}\) ist die Inverse der Matrix, die die Beziehungen zwischen den vorhandenen Datenpunkten darstellt; \(y\) sind die GPS-Aufzeichnungen. Je dichter die Daten liegen, desto größer wird \(K_*\) und desto mehr benachbarte Daten können in Betracht gezogen werden.

Um dies mit einem realen Szenario zu erklären: 1. Zunächst geht man davon aus, dass das Fahrrad überall hinfahren könnte (\(K_{**}\) ist groß) 2. Je mehr GPS-Aufzeichnungen vorhanden sind (\(K_*\) wird größer) 3. Und je konsistentere Aufzeichnungen vorliegen (\(K^{-1}\) stabil) 4. Desto geringer wird die Unsicherheit der Standortvorhersage

Effekt der Formeln auf Daten Die unsicheren Vorhersagen hängen von der Menge an GPS-Daten ab und sehen wie folgt aus: 1. Abschnitt mit häufigen GPS-Aufzeichnungen: geringe Unsicherheit - \(K_*\) ist groß und es gibt viele Daten, so dass \(K_*K^{-1}K_*^T\) groß ist - Daher wird \(\Sigma_*\) klein und der Pfadschätzwert genau 2. Abschnitt mit seltenen GPS-Aufzeichnungen: hohe Unsicherheit - \(K_*\) ist klein und es gibt wenige Daten, so dass \(K_*K^{-1}K_*^T\) klein ist - Daher wird \(\Sigma_*\) groß und die Unsicherheit der Pfadvorhersage hoch

Einfach gesagt, wird \(K\) größer, je dichter die Zeitintervall-Daten liegen, und daher wird die Unsicherheit geringer.

Lassen Sie uns das Beispiel des Fahrradpfads verstehen, um es zu veranschaulichen.

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# 시각화 스타일 설정
sns.set_style("whitegrid")
plt.rcParams['font.size'] = 10

# 데이터셋 1: 5개 관측점
time1 = np.array([0, 2, 5, 8, 10]).reshape(-1, 1)
position1 = np.array([0, 2, 3, 1, 4])

# 데이터셋 2: 8개 관측점
time2 = np.array([0, 1, 2, 4, 5, 6, 8, 10]).reshape(-1, 1)
position2 = np.array([0, 1, 2.5, 1.5, 3, 2, 1, 4])  # 더 큰 변동성 추가

# 예측할 시간점 생성: 0~10분 구간을 100개로 분할
time_pred = np.linspace(0, 10, 100).reshape(-1, 1)

# RBF 커널 함수 정의
def kernel(T1, T2, l=2.0):
    sqdist = np.sum(T1**2, 1).reshape(-1, 1) + np.sum(T2**2, 1) - 2 * np.dot(T1, T2.T)
    return np.exp(-0.5 * sqdist / l**2)

# 가우시안 프로세스 예측 함수
def predict_gp(time, position, time_pred):
    K = kernel(time, time)
    K_star = kernel(time_pred, time)
    K_star_star = kernel(time_pred, time_pred)
    mu_star = K_star.dot(np.linalg.inv(K)).dot(position)
    sigma_star = K_star_star - K_star.dot(np.linalg.inv(K)).dot(K_star.T)
    return mu_star, sigma_star

# 두 데이터셋에 대한 예측 수행
mu1, sigma1 = predict_gp(time1, position1, time_pred)
mu2, sigma2 = predict_gp(time2, position2, time_pred)

# 2개의 서브플롯 생성
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 4))

# 첫 번째 그래프 (5개 데이터)
ax1.fill_between(time_pred.flatten(),
                mu1 - 2*np.sqrt(np.diag(sigma1)),
                mu1 + 2*np.sqrt(np.diag(sigma1)),
                color='blue', alpha=0.2, label='95% confidence interval')
ax1.plot(time_pred, mu1, 'b-', linewidth=1.5, label='Predicted path')
ax1.plot(time1, position1, 'ro', markersize=6, label='GPS records')
ax1.set_xlabel('Time (min)')
ax1.set_ylabel('Position (km)')
ax1.set_title('Route Estimation (5 GPS points)')
ax1.legend(fontsize=8)

# 두 번째 그래프 (8개 데이터)
ax2.fill_between(time_pred.flatten(),
                mu2 - 2*np.sqrt(np.diag(sigma2)),
                mu2 + 2*np.sqrt(np.diag(sigma2)),
                color='blue', alpha=0.2, label='95% confidence interval')
ax2.plot(time_pred, mu2, 'b-', linewidth=1.5, label='Predicted path')
ax2.plot(time2, position2, 'ro', markersize=6, label='GPS records')
ax2.set_xlabel('Time (min)')
ax2.set_ylabel('Position (km)')
ax2.set_title('Route Estimation (8 GPS points)')
ax2.legend(fontsize=8)

plt.tight_layout()
plt.show()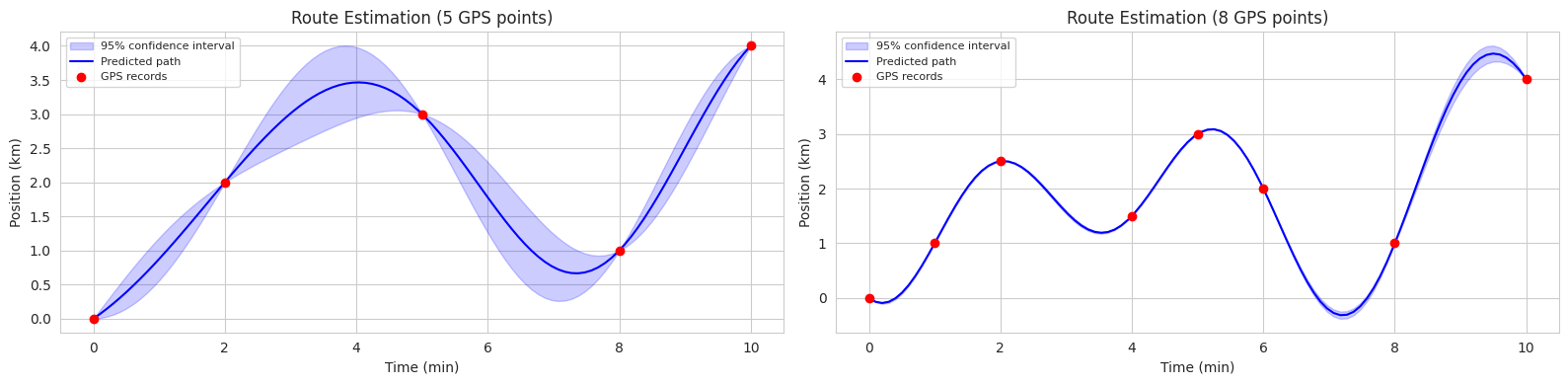

Der folgende Code ist ein Beispiel für die Schätzung von Fahrradstrecken unter Verwendung von GPs in zwei Szenarien (5 Beobachtungspunkte, 8 Beobachtungspunkte). In jedem Diagramm stellt die durchgezogene blaue Linie den vorhergesagten mittleren Pfad dar, während der blau schattierte Bereich das 95%ige Konfidenzintervall zeigt.

• Bei wenigen Daten (linkes Diagramm): Aufgrund der spärlichen GPS-Aufzeichnungen ist die Unsicherheit der Vorhersage (Breite des Konfidenzintervalls) groß.
• Bei vielen Daten (rechtes Diagramm): Mit dichteren GPS-Aufzeichnungen verringert sich die Unsicherheit der Vorhersage, und der vorhergesagte Pfad nähert sich dem tatsächlichen Pfad an.

Auf diese Weise bieten GP nicht nur die Vorhersagergebnisse, sondern auch die Unsicherheit dieser Vorhersagen. Dies macht sie in verschiedenen Bereichen (z.B. autonomes Fahren, Roboterkontrolle, medizinische Diagnostik), in denen Unsicherheiten im Entscheidungsprozess berücksichtigt werden müssen, nützlich.

6.6.2 Moderne Anwendungen

Gaußsche Prozesse werden in verschiedenen wissenschaftlichen und ingenieurtechnischen Bereichen angewendet, wie Robotersteuerung, Optimierung von Sensornetzen, Vorhersage von Molekülstrukturen, Klimamodellierung und Analyse von Astronomiedaten. Ein repräsentatives Anwendungsbeispiel im Maschinelles Lernen ist die Hyperparameter-Optimierung, wie bereits besprochen. Ein weiteres wichtiger Bereich, in dem unsichere Vorhersagen erforderlich sind, sind autonom fahrende Fahrzeuge. Hier wird das zukünftige Positionieren von anderen Fahrzeugen vorhergesagt, und bei hohen Unsicherheiten wird eine vorsichtigere Fahrt durchgeführt. Darüber hinaus werden sie in der Medizin zur Vorhersage von Patientenzuständen und im Finanzmarkt zur Vorhersage von Aktienkursen und zum Managen von Risiken aufgrund von Unsicherheit angewendet. In jüngster Zeit wird die Anwendung von GP in Bereichen wie Verstärkungslernen (Reinforcement Learning), Kombination mit Generativen Modellen im Deep Learning, Kausalinferenz und Metakernen intensiv erforscht.

6.6.3 Tiefes Kernlernverfahren (Deep Kernel Learning)

Der wichtigste Bestandteil von Gaußschen Prozessen ist das Kernmodell (Covarianzfunktion). Deep Learning hat die Stärke, Darstellungen aus Daten zu lernen. Es liegt nahe, eine effektive Kombination der Vorhersagefähigkeiten von GP und den Lernfähigkeiten von tiefen neuronalen Netzen in Bezug auf Darstellung als Forschungsrichtung anzustreben. Ein repräsentatives Verfahren ist das Tiefes Kernlernverfahren (Deep Kernel Learning, DKL), bei dem anstelle eines vordefinierten Kerns wie des RBF-Kerns ein neuronales Netz verwendet wird, um direkt aus den Daten zu lernen.

Die allgemeine Struktur von DKL sieht folgendermaßen aus:

1. Eigenschaftsextraktion (Feature Extraction): Die Eingabedaten werden zunächst durch ein tiefes Neuronales Netz (in der Regel CNN oder Transformer) geleitet, um sie in niedrigdimensionale Eigenschaftsvektoren zu transformieren.
2. Kernberechnung (Kernel Calculation): Mit den berechneten Kernmatrizen und Trainingsdaten wird das Gauß-Prozess-Modell trainiert und Vorhersagen für neue Eingaben (Mittelwerte und Varianzen) durchgeführt.
3. Gaußscher Prozess (Gaussian Process): Die berechneten Kernmatrizen werden verwendet, um ein Gaußsches Prozessmodell zu trainieren und Vorhersagen für neue Eingaben (Mittelwerte und Varianzen) durchzuführen. DKL hat den Vorteil, dass es durch neuronale Netze sowohl nützliche Merkmalsrepräsentationen aus Daten als auch Ähnlichkeiten zwischen Daten gleichzeitig lernen kann. Auf diese Weise können auch komplexe Daten (wie Bilder, Graphen, Texte) mit Berücksichtigung von Unsicherheit vorhergesagt werden.

DKL wird in verschiedenen Bereichen angewendet. * Bildklassifikation (Image Classification): Verwenden von CNNs, um Bildmerkmale zu extrahieren und GP zur Durchführung der Klassifizierung. * Graphenklassifikation (Graph Classification): Verwenden von Graph Neural Networks (GNN), um Merkmale aus der Graphenstruktur zu extrahieren und GP zur Graphenklassifizierung. * Moleküleigenschaftsvorhersage (Molecular Property Prediction): Empfangen von Molekülgraphen als Eingabe, um die Eigenschaften des Moleküls (z. B. Löslichkeit, Toxizität) vorherzusagen. * Zeitreihenvorhersage (Time Series Forecasting): Verwenden von RNNS, um Merkmale aus Zeitreihendaten zu extrahieren und GP zur Vorhersage zukünftiger Werte. Hier führen wir ein einfaches Beispiel für DKL durch und werden in Teil 2 detailliertere Inhalte und Anwendungsbeispiele behandeln.

Tiefgang-Kern-Netzwerke

Zuerst definieren wir tiefgangige Kernnetzwerke. Ein Kernnetzwerk ist ein neuronales Netz, das eine Kernfunktion lernt. Dieses Netzwerk nimmt Eingabedaten auf und gibt eine Merkmalsdarstellung aus. Diese Merkmalsdarstellung wird zur Berechnung der Kernmatrix verwendet.

import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Normal
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# Set seed for reproducibility
torch.manual_seed(42)
np.random.seed(42)

# Define a neural network to learn the kernel
class DeepKernel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(DeepKernel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, output_dim)
        self.activation = nn.ReLU()

    def forward(self, x):
        x = self.activation(self.fc1(x))
        x = self.activation(self.fc2(x))
        x = self.fc3(x)  # No activation on the final layer
        return x

Die Eingabe eines tiefen Kernels Neuronalen Netzes ist in der Regel ein 2D-Tensor, wobei die erste Dimension die Batch-Größe und die zweite Dimension die Dimension der Eingangsdaten ist. Die Ausgabe ist ein 2D-Tensor mit der Form (Batch-Größe, Dimensionsgröße der Merkmalsdarstellung).

GP-Schichtdefinition

Die GP-Schicht nimmt die Ausgabe des tiefen Kernel-Netzwerks entgegen, berechnet die Kernel-Matrix und bestimmt die Vorhersageverteilung.

import torch
import torch.nn as nn

# Define the Gaussian Process layer
class GaussianProcessLayer(nn.Module):
    def __init__(self, num_dim, num_data):
        super(GaussianProcessLayer, self).__init__()
        self.num_dim = num_dim
        self.num_data = num_data
        self.lengthscale = nn.Parameter(torch.ones(num_dim))  # Length-scale for each dimension
        self.noise_var = nn.Parameter(torch.ones(1))  # Noise variance
        self.outputscale = nn.Parameter(torch.ones(1))  # Output scale

    def forward(self, x, y):
        # Calculate the kernel matrix (using RBF kernel)
        dist_matrix = torch.cdist(x, x)  # Pairwise distances between inputs
        kernel_matrix = self.outputscale * torch.exp(-0.5 * dist_matrix**2 / self.lengthscale**2)
        kernel_matrix += self.noise_var * torch.eye(self.num_data)

        # Calculate the predictive distribution (using Cholesky decomposition)
        L = torch.linalg.cholesky(kernel_matrix)
        alpha = torch.cholesky_solve(y.unsqueeze(-1), L)  # Add unsqueeze for correct shape
        predictive_mean = torch.matmul(kernel_matrix, alpha).squeeze(-1) # Remove extra dimension
        v = torch.linalg.solve_triangular(L, kernel_matrix, upper=False)
        predictive_var = kernel_matrix - torch.matmul(v.T, v)


        return predictive_mean, predictive_var

        return predictive_mean, predictive_var

Die Eingabe der GP-Schicht ist ein 2D-Tensor mit der Form (Batch-Größe, Dimension der Merkmalsdarstellung). Die Ausgabe ist ein Tupel, das die vorhergesagten Mittelwerte und Varianzen enthält. Für die Berechnung der Kernmatrix wird der RBF-Kern verwendet, und um die Berechnungseffizienz zu erhöhen, wird die Cholesky-Zerlegung zur Berechnung der Vorhersageverteilung genutzt. y.unsqueeze(-1) und .squeeze(-1) dienen dazu, die Dimensionen zwischen y und der Kernmatrix abzugleichen.

# 데이터를 생성
x = np.linspace(-10, 10, 100)
y = np.sin(x) + 0.1 * np.random.randn(100)

# 데이터를 텐서로 변환
x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(-1)  # (100,) -> (100, 1)
y_tensor = torch.tensor(y, dtype=torch.float32)  # (100,)


# 딥 커널과 GP 레이어를 초기화
deep_kernel = DeepKernel(input_dim=1, hidden_dim=50, output_dim=1)  # output_dim=1로 수정
gp_layer = GaussianProcessLayer(num_dim=1, num_data=len(x))

# 손실 함수와 최적화기를 정의
loss_fn = nn.MSELoss()  # Use MSE loss
optimizer = optim.Adam(list(deep_kernel.parameters()) + list(gp_layer.parameters()), lr=0.01)

num_epochs = 100
# 모델을 학습
for epoch in range(num_epochs):
    optimizer.zero_grad()
    kernel_output = deep_kernel(x_tensor)
    predictive_mean, _ = gp_layer(kernel_output, y_tensor) # predictive_var는 사용 안함
    loss = loss_fn(predictive_mean, y_tensor)  # Use predictive_mean here
    loss.backward()
    optimizer.step()
    if(epoch % 10 == 0):
        print(f'Epoch {epoch+1}, Loss: {loss.item()}')

# 예측을 수행
with torch.no_grad():
    kernel_output = deep_kernel(x_tensor)
    predictive_mean, predictive_var = gp_layer(kernel_output, y_tensor)

# 결과를 시각화
sns.set()
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'bo', label='Training Data')
plt.plot(x, predictive_mean.numpy(), 'r-', label='Predictive Mean')
plt.fill_between(x, predictive_mean.numpy() - 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
                 predictive_mean.numpy() + 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
                 alpha=0.2, label='95% CI')
plt.legend()
plt.show()

Epoch 1, Loss: 4.3467857893837725e-13
Epoch 11, Loss: 3.1288711313699757e-13
Epoch 21, Loss: 3.9212150236903054e-13
Epoch 31, Loss: 4.184870765894244e-13
Epoch 41, Loss: 2.9785689973499396e-13
Epoch 51, Loss: 3.8607078688482344e-13
Epoch 61, Loss: 3.9107123572454383e-13
Epoch 71, Loss: 2.359286811054462e-13
Epoch 81, Loss: 3.4729958167147024e-13
Epoch 91, Loss: 2.7600995490886793e-13

/tmp/ipykernel_1408185/2425174321.py:40: RuntimeWarning: invalid value encountered in sqrt
  plt.fill_between(x, predictive_mean.numpy() - 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
/tmp/ipykernel_1408185/2425174321.py:41: RuntimeWarning: invalid value encountered in sqrt
  predictive_mean.numpy() + 1.96 * np.sqrt(predictive_var.numpy().diagonal()),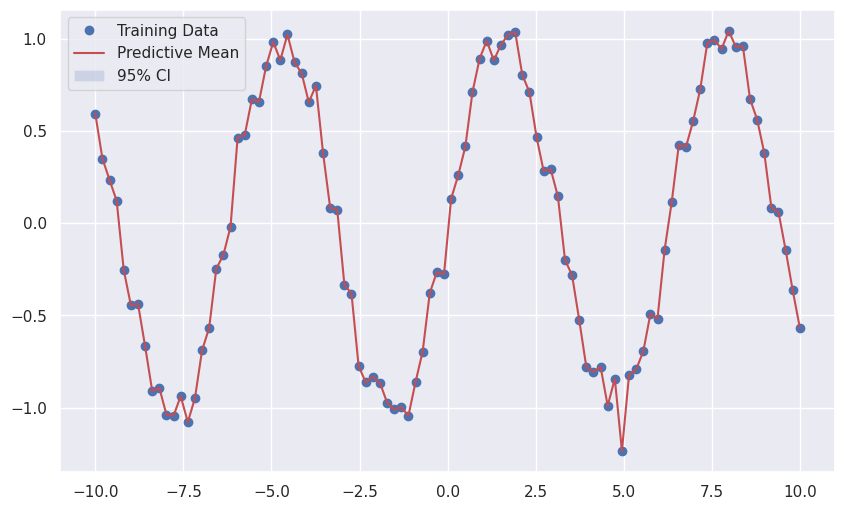

Das Modelltraining verwendet die Mean Squared Error (MSE) Verlustfunktion und den Adam-Optimierer, um die Parameter des tiefen Kernnetzes und der GP-Schicht simultan zu lernen.

6.6.4 Möglichkeiten und Grenzen des DKL

Das vorangegangene Beispiel zeigt die grundlegende Idee des Deep Kernel Learning (DKL). Es verwendet ein Deep-Learning-Modell (DeepKernel Klasse), um Merkmale der Eingangsdaten zu extrahieren, und diese Merkmale werden dann verwendet, um den Kern eines Gaußschen Prozesses (GP) zu berechnen. Anschließend wird GP verwendet, um den Mittelwert und die Varianz (Unsicherheit) der Vorhersage zu berechnen. Auf diese Weise kombiniert DKL die Fähigkeiten des Deep Learnings zur Merkmalsrepräsentation mit der Unsicherheitsquantifizierung von GPs, um auch bei komplexen Daten verlässliche Vorhersagen zu ermöglichen.

Möglichkeiten des DKL:

• Daten-Effizienz: GP tendieren dazu, auch bei wenigen Daten gut zu funktionieren. DKL kombiniert die leistungsfähige Merkmalsextraktion von Deep Learning mit der Daten-Effizienz von GPs und kann daher auch bei wenigen Daten gute Leistungen erzielen.
• Unsicherheitsquantifizierung: DKL kann die Unsicherheit einer Vorhersage quantifizieren. Dies ist in sicherheitskritischen Anwendungen (z.B. medizinische Diagnose, autonome Fahrt) sehr nützlich.
• Flexibilität: DKL kann auf verschiedene Arten von Daten (Bilder, Text, Graphen usw.) angewendet werden. Man kann die neuronale Netzarchitektur frei wählen und passende Merkmalsextraktoren für das Problem entwickeln.
• Kombination mit Bayes’scher Optimierung: DKL kann mit Bayes’scher Optimierung kombiniert werden, um die Hyperparameter des Modells effizient zu tunen.

Grenzen des DKL:

• Berechnungsaufwand: GP sind immer noch rechenintensiv. Insbesondere wenn das Trainingsdatensatz groß wird, wächst auch die Größe der Kernelsmatrix und macht Berechnungen schwierig.
• Netzwerkdesign: Die Leistung von DKL hängt stark vom Design des Merkmalsextraktors (neuronales Netz) ab. Die Auswahl einer geeigneten neuronalen Netzarchitektur ist weiterhin eine komplexe Aufgabe.
• Mangel an theoretischem Verständnis: Die theoretische Analyse von DKL befindet sich noch in den Anfängen. Weitere Forschung ist notwendig, um zu verstehen, warum und unter welchen Bedingungen DKL gut funktioniert.

Dieses Kapitel stellt verschiedene Techniken vor, die auf unterschiedliche Weise das Problem des Overfitting ansprechen:

• Regularisierung: Es werden Penaltys für die Komplexität des Modells eingeführt, um zu verhindern, dass die Gewichte zu groß werden. (L1, L2, Elastic Net)
• Dropout: Während des Trainings werden zufällige Neuronen deaktiviert, um eine Überanpassung an bestimmte Neuronen oder Kombinationen von Neuronen zu verhindern.
• Batch-Normalisierung: Die Eingaben jeder Schicht werden normalisiert, um das Training zu stabilisieren und zu beschleunigen.
• Hyperparameter-Optimierung: Es werden Methoden wie die Bayes’sche Optimierung verwendet, um Kombinationen von Hyperparametern zu finden, die die Leistung des Modells optimieren.
• Gaußscher Prozess, Deep Kernel Learning: Die Unsicherheit wird explizit modelliert, um verlässlichere Vorhersagen zu ermöglichen. Die angemessene Kombination dieser Techniken und das Anpassen an die Eigenschaften des Problems ist eine der wichtigsten Fähigkeiten eines Deep-Learning-Ingineurs. Es gibt keine “perfekte Lösung für alle Fälle”, und der optimale Weg muss durch Experimente und Analysen gefunden werden. Die Deep-Learning-Forschung entwickelt sich kontinuierlich und rasch, und es werden ständig neue Methoden zur Behebung von Overfitting eingeführt.

Übungsaufgaben

Grundlegende Aufgaben

1. Erkläre die Konzepte von Overfitting und Underfitting, und beschreibe, wie sich diese Phänomene auf die Leistung des Modells auswirken.
2. Beschreibe den Unterschied zwischen L1-Regulierung und L2-Regulierung, und erläutere, wie jede Regulierung die Gewichte des Modells beeinflusst.
3. Erkläre das Funktionsprinzip von Dropout und beschreibe, wie Dropout bei der Verhinderung von Overfitting hilft.
4. Erkläre den Konzepten von Batch Normalization und beschreibe die Vorteile, die Batch Normalization für das Lernen tiefster neuronaler Netze bietet.
5. Ändere die Lambda-Werte in der custom_loss-Funktion des gegebenen Codes und beschreibe, welche Veränderungen im Diagramm auftreten.
6. Definiere die L1- und L2-Norm.
7. Erkläre, wie Mittelwert und Varianz in den Formeln für Batch Normalization berechnet werden, und wie diese in den Normalisierungsprozess eingesetzt werden.

Anwendungsprobleme

1. Trainiere ein Polynomregressionsmodell auf einem gegebenen Datensatz und beobachte die Phänomene von Overfitting und Underfitting durch Ändern des Grades (degree). (Python-Code schreiben)
2. Erstelle ein einfaches neuronales Netzwerk, wende L1- oder L2-Regulierung an, beobachte die Veränderungen der Gewichte des Modells und vergleiche die Leistungsänderungen in Abhängigkeit von der Regulierungsstärke. (Python-Code schreiben)
3. Trainiere neuronale Netze mit unterschiedlichen Dropout-Raten und vergleiche den Trainings- und Validierungsaufwand sowie die Genauigkeit für jede Rate. (Python-Code schreiben)
4. Vergleiche die Lernrate und die Konvergenzstabilität des neuronalen Netzwerks, indem du Schichten der Batch Normalization hinzufügst oder entfernst. (Python-Code schreiben)
5. Leite die Optimalitätsbedingungen für eine verlustfunktion mit angewandter L1- und L2-Regulierung her, indem du das Lagrange-Multiplikatorenverfahren verwendest.
6. Leite den Backpropagation-Prozess der Batch Normalization her und beschreibe, wie sie bei der Milderung des Gradientenverschwindungsproblems hilft.

Vertiefende Aufgaben

1. Visualisiere die Auswirkungen von L1-Regulierung und L2-Regulierung auf das Verlustflächen und erkläre die geometrische Bedeutung jeder Regulierung. (Python-Code schreiben)
2. Interpretiere Dropout im Kontext des Ensemble-Lernens und beschreibe, wie es zur Schätzung der Modellunsicherheit genutzt werden kann.
3. Vergleiche verschiedene Hyperparameteroptimierungsverfahren (Grid Search, Random Search, Bayesian Optimization usw.) und erläutere die Vor- und Nachteile jeder Methode.
4. Implementiere den Kerngedanken der bayesianischen Optimierung, um das Optimum einer einfachen Funktion zu finden, ohne BoTorch zu verwenden. (Python-Code schreiben, Bibliotheken sind zulässig)
5. Erkläre die grundlegenden Prinzipien eines Gaußprozesses und beschreibe, wie ein Gaußprozess Vorhersagen mit Unsicherheit macht.
6. Beschreibe die Bedingungen, die von einer Kernelfunktion (kernel function) eines Gaußprozesses erfüllt sein müssen, und beweise, dass die RBF-Kernelfunktion diese Bedingung erfüllt.
7. Erkläre die Rolle der Akquisefunktion in der bayesianischen Optimierung, leite die Formel für die Expected Improvement (EI) her und erläutere ihre Bedeutung.

Klicken Sie hier, um den Inhalt anzuzeigen (Lösungen zu Übungsproblemen)

Übungsantworten

Grundfragen

1. Überanpassung/Unteranpassung:
   • Überanpassung (Overfitting): Das Modell passt sich zu gut an die Trainingsdaten an, sodass die Leistung auf neuen Daten (Validierungs-/Testdaten) schlechter wird. Die Leistung auf den Trainingsdaten ist hoch, aber auf Validierungs-/Testdaten niedrig.
   • Unteranpassung (Underfitting): Das Modell ist zu einfach und kann die Muster in den Trainingsdaten nicht ausreichend lernen. Es zeigt eine geringe Leistung sowohl bei Trainings-, Validierungs- als auch Testdaten.
2. L1/L2-Regularisierung:
   • L1-Regularisierung (Lasso): Fügt die Summe der Beträge der Gewichte zur Verlustfunktion hinzu. \(\lambda \sum_{i} |w_i|\) Dies setzt einige Gewichte exakt auf 0, was einen Feature-Selektions-Effekt erzeugt.
   • L2-Regularisierung (Ridge): Fügt die Summe der Quadrate der Gewichte zur Verlustfunktion hinzu. \(\lambda \sum_{i} (w_i)^2\) Dies bringt die Gewichte nahe an 0, setzt sie aber nicht vollständig auf 0.
3. Dropout:
   • Funktionsweise: Deaktiviert während des Trainings zufällige Neuronen (setzt ihre Ausgabe auf 0).
   • Überanpassungsverhinderung: Da jedes Mal andere Neuronenkombinationen trainiert werden, wird eine Abhängigkeit von bestimmten Neuronen verhindert und ein Ensembles-Lern-Effekt erzeugt.
4. Batch-Normalisierung:
   • Konzept: Normalisiert die Eingaben jeder Schicht auf Mittelwert 0 und Varianz 1.
   • Vorteile: Verbesserte Lernrate, Milderung von Gradientenverschwindungs-/Explosionsproblemen, Möglichkeit höherer Lernraten zu verwenden, leichter Regularisierungseffekt.
5. custom_loss-Lambda-Veränderung:
   • Erhöhung von lambda: Der Einfluss des Regularisierungsterms wird größer. Die Gewichte werden kleiner und das Modell einfacher, was die Wahrscheinlichkeit einer Unteranpassung erhöht.
   • Verringern von lambda: Der Einfluss des Regularisierungsterms wird geringer. Die Gewichte werden größer und das Modell komplexer, was die Wahrscheinlichkeit einer Überanpassung erhöht.
6. L1/L2-Regularisierung:
   • L1-Norm (Manhattan-Distanz): Summe der Beträge der Elemente. \(\|x\|_1 = \sum_{i=1}^{n} |x_i|\)
   • L2-Norm (Euklidische Distanz): Quadratwurzel der Summe der Quadrate der Elemente. \(\|x\|_2 = \sqrt{\sum_{i=1}^{n} x_i^2}\)
7. Batch-Normalisierung:
   • Mittelwert (μ): Mittelwert der Samples in einem Minibatch. \(\mu = \frac{1}{m} \sum_{i=1}^{m} x_i\)
   • Varianz (σ²): Varianz der Samples in einem Minibatch. \(\sigma^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu)^2\)
   • Normalisierung: \(x_{i\_\text{norm}} = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\) (ε ist eine kleine Konstante, um eine Division durch 0 zu vermeiden)

Anwendungsfragen

1. Polynomielle Regression: (Code weggelassen) Eine zu hohe Ordnung führt zu Überanpassung, eine zu niedrige zu Unteranpassung.

2. L1/L2-Regularisierung: (Code weggelassen) Je stärker die Regularisierungsstärke (lambda) ist, desto kleiner werden die Gewichte und desto größer sind die Leistungsänderungen.

3. Dropout-Rate: (Code weggelassen) Eine angemessene Dropout-Rate kann Überanpassung verhindern und die Leistung verbessern. Zu hohe Raten können zu Unteranpassung führen.

4. Batch-Normalisierung: (Code weggelassen) Die Hinzufügung von Batch-Normalisierung beschleunigt das Lernen und fördert eine stabile Konvergenz.

5. Lagrange-Multiplikatorenmethode:

   • L2-Regularisierung: \(L(\mathbf{w}, \lambda) = \text{Loss}(\mathbf{w}) + \lambda (\|\mathbf{w}\|_2^2 - c) \rightarrow \nabla_\mathbf{w}L = \nabla_\mathbf{w}\text{Loss}(\mathbf{w}) + 2\lambda\mathbf{w} = 0\)
   • L1-Regularisierung: \(L(\mathbf{w}, \lambda) = \text{Loss}(\mathbf{w}) + \lambda (\|\mathbf{w}\|_1 - c) \rightarrow \nabla_\mathbf{w}L = \nabla_\mathbf{w}\text{Loss}(\mathbf{w}) + \lambda \cdot \text{sign}(\mathbf{w}) = 0\) (sign(w) ist das Vorzeichen von w)

6. Backpropagation bei Batch-Normalisierung: (Herleitung weggelassen) Batch-Normalisierung normiert die Eingaben jeder Schicht, um Probleme mit verschwindenden oder explodierenden Gradienten zu mildern und das Lernen zu stabilisieren.

Vertiefungsfragen

1. Visualisierung der Verlustebene: (Code weggelassen) L1-Regularisierung erzeugt rautenförmige, L2-Regularisierung kreisförmige Restriktionsbedingungen, sodass die optimalen Lösungen an verschiedenen Positionen entstehen.

2. Dropout-Ensemble: Dropout hat den Effekt, dass das Modell bei jedem Trainingsdurchgang mit unterschiedlichen Netzwerkstrukturen trainiert wird, ähnlich wie Ensemble-Lernen. Bei der Vorhersage werden alle Neuronen verwendet (ohne Dropout), um eine durchschnittliche Vorhersage zu treffen. Durch Monte-Carlo-Dropout kann die Unsicherheit der Vorhersagen geschätzt werden.

3. Methoden zur Hyperparameter-Optimierung:

   • Grid Search: Alle Kombinationen ausprobieren. Sehr hoher Rechenaufwand.
   • Random Search: Zufällige Kombinationen ausprobieren. Kann effizienter sein als Grid Search.
   • Bayesianische Optimierung: Verwendet ein Wahrscheinlichkeitsmodell auf Basis früherer Suchergebnisse, um den nächsten Suchpunkt zu bestimmen. Effizient.

4. Implementierung der bayesianischen Optimierung: (Code weggelassen) Verwendet ein Stellvertretermodell (z.B. Gaußscher Prozess) und eine Erwerbfunktion (z.B. Expected Improvement).

5. Gaußscher Prozess: Eine Wahrscheinlichkeitsverteilung über Funktionen. Definiert die Kovarianz zwischen Funktionswerten mit Hilfe einer Kernfunktion. Berechnet auf Basis der gegebenen Daten eine posteriore Verteilung, um den Mittelwert und die Varianz (Unsicherheit) der Vorhersage zu liefern.

6. Bedingungen für Kernfunktionen: Sie müssen positiv semidefinit sein. Die durch beliebige Eingangspunkte erzeugten Kernmatrizen (Gram-Matrix) müssen positiv semidefinite Matrizen sein. Der RBF-Kern erfüllt diese Bedingung. (Beweis weggelassen)

7. Erwerbfunktionen: In der bayesianischen Optimierung werden sie verwendet, um den nächsten Suchpunkt zu bestimmen. Expected Improvement (EI) berücksichtigt sowohl die Wahrscheinlichkeit als auch das Ausmaß einer Verbesserung gegenüber dem bisherigen Optimum, um den nächsten Suchpunkt auszuwählen. (Herleitung der Formeln weggelassen)

1. Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Srivastava et al., 2014): Das ursprüngliche Papier, das den Begriff und die Wirkung von Dropout erläutert. (https://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf)
2. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe & Szegedy, 2015): Das ursprüngliche Papier, das den Begriff und die Wirkung von Batch Normalisierung erläutert. (https://arxiv.org/abs/1502.03167)
3. Deep Learning (Goodfellow et al., 2016): Ein Lehrbuch über Deep Learning. Kapitel 7 “Regularization for Deep Learning” behandelt Overfitting und Regularisierungstechniken detailliert. (http://www.deeplearningbook.org/)
4. Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): Erklärt die Lernschwierigkeiten bei frühen Deep-Learning-Modellen und die Bedeutung von Gewichtsinitialisierungsmethoden. (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)
5. Regularization techniques for deep learning: A survey (Kukacka et al., 2017): Ein Überblick, der verschiedene Regularisierungstechniken vergleicht und analysiert.
6. A Tutorial on Bayesian Optimization (Frazier, 2018): Ein Tutorial, das die grundlegenden Konzepte und Anwendungen von Bayes’scher Optimierung erläutert. (https://arxiv.org/abs/1807.02811)
7. Bayesian Optimization (Garnett, 2023): Ein umfassendes Lehrbuch über Bayes’sche Optimierung (https://www.bayesoptbook.com/)
8. Gaussian Processes for Machine Learning (Rasmussen & Williams, 2006): Ein Lehrbuch, das die grundlegenden Prinzipien und Anwendungen von Gaußschen Prozessen in der Maschinenlernen behandelt. (http://www.gaussianprocess.org/gpml/)
9. Deep Kernel Learning (Wilson et al., 2016): Ein Papier, das den Begriff und die Methoden des Deep-Kernel-Lernens erläutert. (https://arxiv.org/abs/1511.02222)
10. Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow (Aurélien Géron, 2019): Ein praktisches Lehrbuch über Maschinelles Lernen und Deep Learning. Es erklärt Overfitting und Regularisierungstechniken anhand von Code-Beispielen.
11. Adam: A Method for Stochastic Optimization (Kingma & Ba, 2014) (https://arxiv.org/abs/1412.6980): Ein Papier über den Adam-Optimierer
12. Decoupled Weight Decay Regularization (Loshchilov & Hutter, 2017) (https://arxiv.org/abs/1711.05101): Ein Papier über AdamW
13. Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Srivastava et al., 2014): Das ursprüngliche Papier, das den Konzept und die Effekte von Dropout erklärt. (https://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf) 2. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe & Szegedy, 2015): Das ursprüngliche Papier, das den Konzept und die Effekte von Batch-Normalisierung erklärt. (https://arxiv.org/abs/1502.03167) 3. Deep Learning (Goodfellow et al., 2016): Ein Lehrbuch über Deep Learning. Kapitel 7 “Regularization for Deep Learning” behandelt Overfitting und Regularisierungstechniken detailliert. (http://www.deeplearningbook.org/) 4. Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): Erklärt die Schwierigkeiten beim Training von frühen Deep-Learning-Modellen und die Bedeutung von Gewichtsinitialisierungsmethoden. (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf) 5. Regularization techniques for deep learning: A survey (Kukacka et al., 2017): Ein Paper, das verschiedene Regularisierungstechniken umfassend vergleicht und analysiert. 6. A Tutorial on Bayesian Optimization (Frazier, 2018): Eine Einführung in die grundlegenden Konzepte und Anwendungen der bayesischen Optimierung. (https://arxiv.org/abs/1807.02811) 7. Bayesian Optimization (Garnett, 2023): Ein umfassendes Lehrbuch zur bayesischen Optimierung (https://www.bayesoptbook.com/) 8. Gaussian Processes for Machine Learning (Rasmussen & Williams, 2006): Ein Lehrbuch über die grundlegenden Prinzipien und Anwendungen von Gaußprozessen in der Maschinelles Lernen. (http://www.gaussianprocess.org/gpml/) 9. Deep Kernel Learning (Wilson et al., 2016): Ein Paper, das den Konzept und die Methoden des tiefen Kernels Lernens erklärt. (https://arxiv.org/abs/1511.02222) 10. Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow (Aurélien Géron, 2019): Ein praktisches Lehrbuch zum Maschinelles Lernen und Deep Learning. Es erklärt Overfitting und Regularisierungstechniken anhand von Codebeispielen. 11. Adam: A Method for Stochastic Optimization (Kingma & Ba, 2014) (https://arxiv.org/abs/1412.6980): Ein Paper über den Adam-Optimierer 12. Entkoppelte Gewichtszerfallregularisierung (Loshchilov & Hutter, 2017) (https://arxiv.org/abs/1711.05101): Papier über AdamW

Original text:

번역:

Das ist der zu übersetzende Text.