Code
!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local
%load_ext autoreload
%autoreload 2 
8. Kapitel Die Geburt des Transformers
“Attention is all you need.” - Ashish Vaswani et al., NeurIPS 2017.
Im Jahr 2017 war in der Geschichte der Natürlichen Sprachverarbeitung eine besondere Rolle gespielt worden, da Google den Transformer in dem Paper “Attention is All You Need” veröffentlicht hat. Dies kann mit der Revolution verglichen werden, die AlexNet 2012 im Bereich Computer Vision ausgelöst hat. Durch das Erscheinen des Transformers trat die Natürliche Sprachverarbeitung (NLP) in ein neues Zeitalter ein. Danach erschienen starke Sprachmodelle wie BERT und GPT, basierend auf dem Transformer, welche eine neue Ära der Künstlichen Intelligenz eröffneten.
Hinweise
Kapitel 8 stellt den Prozess dar, wie das Google-Forschungsteam den Transformer entwickelt hat, als dramatische Szene. Basierend auf verschiedenen Quellen wie dem Originalpaper, Forschungsblogs und akademischen Präsentationen, versucht es, die Herausforderungen und Problemlösungsprozesse, denen die Forscher möglicherweise gegenüberstanden haben könnten, lebhaft zu beschreiben. Dabei wird geklärt, dass einige Inhalte auf vernünftigen Schlussfolgerungen und Vorstellungskraft basieren.
8.1 Transformer - Die Revolution in der Sequenzverarbeitung
Herausforderung: Wie können die fundamentalen Grenzen bestehender rekurrenter neuronaler Netzwerke (RNN) überwunden werden?
Forscherfrust: Zu dieser Zeit dominierten Modelle auf Basis von RNN, LSTM und GRU das Gebiet der Natürlichen Sprachverarbeitung. Diese Modelle mussten die Eingabesequenzen sequentiell verarbeiten, was es unmöglich machte, sie zu parallelisieren, und bei der Verarbeitung langer Sätze führten sie zu Problemen mit langfristigen Abhängigkeiten. Die Forscher mussten diese fundamentalen Grenzen überwinden und eine neue Architektur entwickeln, die schneller, effizienter und in der Lage war, lange Kontexte gut zu verstehen.
Die Natürliche Sprachverarbeitung war seit Langem an den Grenzen sequentieller Verarbeitung gefesselt. Sequentielle Verarbeitung bedeutet, dass Sätze wortweise oder tokenweise nacheinander verarbeitet werden müssen. Ebenso wie Menschen Wörter nacheinander lesen, mussten auch RNN und LSTM die Eingaben in der Reihenfolge verarbeiten. Diese Art von sequentieller Verarbeitung hatte zwei ernsthafte Probleme. 1. Sie konnte Hardware für parallele Verarbeitung, wie GPU, nicht effektiv nutzen; 2. Bei der Verarbeitung langer Sätze kam es zu einem “Problem langfristiger Abhängigkeiten (long-range dependency problem)”, bei dem Informationen am Anfang des Satzes nicht ordnungsgemäß an das Ende übertragen wurden. Anders ausgedrückt: Elemente im Satz, die in Beziehung zueinander stehen, konnten nicht korrekt verarbeitet werden, wenn sie weit auseinanderlagen.
2017 entwickelte das Google-Forschungsteam den Transformer, um die Leistung der maschinellen Übersetzung drastisch zu verbessern. Der Transformer löste diese Grenzen grundlegend auf. Er entfernte RNN vollständig und führte eine Verarbeitung von Sequenzen ein, die nur auf Selbst-Aufmerksamkeit (self-attention) basiert.
Der Transformer hat drei wesentliche Vorteile: 1. Parallele Verarbeitung: Alle Positionen in einer Sequenz können gleichzeitig verarbeitet werden, um die maximale Nutzung von GPU zu ermöglichen. 2. Globale Abhängigkeiten: Jedes Token kann eine direkte Beziehungskraft zu jedem anderen Token definieren. 3. Flexibler Umgang mit Ortsinformationen: Durch positionale Codierung können Reihenfolgeinformationen effektiv dargestellt werden, während gleichzeitig flexibel auf Sequenzen unterschiedlicher Länge reagiert wird. Der Transformer wurde bald Grundlage leistungsfähiger Sprachmodelle wie BERT und GPT und erweiterte sich auf andere Bereiche, wie den Vision Transformer. Der Transformer ist nicht nur eine neue Architektur, sondern hat die Informationsverarbeitung in der Tiefenlernen grundlegend neu überdacht. Insbesondere im Bereich der Computer Vision führte der Erfolg von ViT (Vision Transformer) dazu, dass es zu einem mächtigen Wettbewerber für CNNs wurde.
8.2 Die Evolution des Transformers
Anfang 2017 stieß ein Forschungsteam von Google auf Schwierigkeiten im Bereich der maschinellen Übersetzung. Die damals vorherrschenden RNN-basierten seq-to-seq-Modelle hatten das anhaltende Problem, dass ihre Leistung bei der Verarbeitung langer Sätze stark nachließ. Das Team unternahm vielfältige Anstrengungen, um die RNN-Architektur zu verbessern, doch diese Maßnahmen blieben vorübergehend und konnten das Kernproblem nicht grundlegend lösen. In diesem Zusammenhang fiel einem Forscher die 2014 veröffentlichte Aufmerksamkeitsmechanismen (Bahdanau et al., 2014) auf. “Wenn die Aufmerksamkeit das Problem der langfristigen Abhängigkeiten lindern konnte, könnte es dann nicht auch ohne RNN und nur mit Aufmerksamkeit möglich sein, Sequenzen zu verarbeiten?”
Viele Menschen geraten beim ersten Kontakt mit dem Aufmerksamkeitsmechanismus in Verwirrung, insbesondere bei den Konzepten Q, K, V. Tatsächlich war die ursprüngliche Form der Aufmerksamkeit das “alignment score” (Ausrichtungspunktzahl), das erstmals 2014 in Bahdanau’s Arbeit beschrieben wurde. Dies war eine Bewertung, die anzeigte, auf welche Teile des Encoders sich der Decoder bei der Erzeugung von Ausgabewörtern konzentrieren sollte. Im Wesentlichen war dies eine Zahl, die die Relevanz zwischen zwei Vektoren darstellte.
Wahrscheinlich begann das Forschungsteam mit der praktischen Frage: “Wie kann man die Beziehungen zwischen Wörtern quantifizieren?” Sie starteten mit einer relativ einfachen Idee, bei der sie die Ähnlichkeit von Vektoren berechneten und diese als Gewichte verwendeten, um kontextuelle Informationen zusammenzufassen. In den frühen Entwurfsdokumenten des Google-Forschungsteams (“Transformers: Iterative Self-Attention and Processing for Various Tasks”) wurden statt der Begriffe Q, K, V Methoden verwendet, die “alignment score” ähnliche Weise die Beziehungen zwischen Wörtern darstellten.
Lassen Sie uns nun den Prozess, mit dem Google-Forscher das Problem lösten, nachvollziehen, um den Aufmerksamkeitsmechanismus zu verstehen. Wir werden von der grundlegenden Idee des Vektoraufberechnung beginnend bis hin zur endgültigen Fertigstellung der Transformer-Architektur Schritt für Schritt die Prozesse erklären.
8.2.1 Die Grenzen der RNN und die Geburt der Aufmerksamkeit
Das Team wollte zunächst die Grenzen der RNN klar erkennen. Durch Experimente stellten sie fest, dass sich die BLEU-Score stark verschlechterte, je länger die Sätze wurden, insbesondere ab 50 Wörtern. Ein größeres Problem war jedoch, dass wegen des sequenziellen Verarbeitungsansatzes von RNNs, selbst mit GPU-Unterstützung, grundlegende Geschwindigkeitsverbesserungen schwierig waren. Um diese Grenzen zu überwinden, analysierte das Team den Aufmerksamkeitsmechanismus, der von Bahdanau et al. (2014) vorgeschlagen wurde. Die Aufmerksamkeit ermöglichte es dem Decoder, alle Zustände des Encoders zu berücksichtigen, um das Problem der langfristigen Abhängigkeiten abzumildern. Im Folgenden ist die grundlegende Implementierung des Aufmerksamkeitsmechanismus gezeigt.
Code
import numpy as np
# Example word vectors (3-dimensional)
word_vectors = {
'time': np.array([0.2, 0.8, 0.3]), # In reality, these would be hundreds of dimensions
'flies': np.array([0.7, 0.2, 0.9]),
'like': np.array([0.3, 0.5, 0.2]),
'an': np.array([0.1, 0.3, 0.4]),
'arrow': np.array([0.8, 0.1, 0.6])
}
def calculate_similarity_matrix(word_vectors):
"""Calculates the similarity matrix between word vectors."""
X = np.vstack(list(word_vectors.values()))
return np.dot(X, X.T)The autoreload extension is already loaded. To reload it, use:
%reload_ext autoreload8.2.2 Grundlegende Konzepte der Aufmerksamkeit
Der Inhalt, der in diesem Abschnitt erklärt wird, stammt aus einem frühen Entwurfsdokument namens “Transformers: Iterative Self-Attention and Processing for Various Tasks”. Wir werden den folgenden Code schrittweise zur Erklärung des grundlegenden Aufmerksamkeitskonzepts durchgehen. Zuerst betrachten wir die Ähnlichkeitsmatrix (Schritte 1 und 2 im Quellcode). Wörter haben in der Regel Hunderte von Dimensionen. Hier werden sie exemplarisch als 3-dimensionale Vektoren dargestellt. Wenn man diese zu einer Matrix formt, besteht diese einfach aus Spaltenvektoren, wobei jede Spalte ein Wortvektor ist. Durch Transponieren (transpose) dieser Matrix wird eine Matrix erzeugt, in der die Wortvektoren Zeilenvektoren sind. Die Multiplikation dieser beiden Matrizen führt dazu, dass jedes Element (i, j) das Skalarprodukt des i-ten und j-ten Wortvektors darstellt, was dem Abstand (Ähnlichkeit) zwischen den beiden Wörtern entspricht.
Code
import numpy as np
def visualize_similarity_matrix(words, similarity_matrix):
"""Visualizes the similarity matrix in ASCII art format."""
max_word_len = max(len(word) for word in words)
col_width = max_word_len + 4
header = " " * (col_width) + "".join(f"{word:>{col_width}}" for word in words)
print(header)
for i, word in enumerate(words):
row_str = f"{word:<{col_width}}"
row_values = [f"{similarity_matrix[i, j]:.2f}" for j in range(len(words))]
row_str += "".join(f"[{value:>{col_width-2}}]" for value in row_values)
print(row_str)
# Example word vectors (in practice, these would have hundreds of dimensions)
word_vectors = {
'time': np.array([0.2, 0.8, 0.3]),
'flies': np.array([0.7, 0.2, 0.9]),
'like': np.array([0.3, 0.5, 0.2]),
'an': np.array([0.1, 0.3, 0.4]),
'arrow': np.array([0.8, 0.1, 0.6])
}
words = list(word_vectors.keys()) # Preserve order
# 1. Convert word vectors into a matrix
X = np.vstack([word_vectors[word] for word in words])
# 2. Calculate the similarity matrix (dot product)
similarity_matrix = calculate_similarity_matrix(word_vectors)
# Print results
print("Input matrix shape:", X.shape)
print("Input matrix:\n", X)
print("\nInput matrix transpose:\n", X.T)
print("\nSimilarity matrix shape:", similarity_matrix.shape)
print("Similarity matrix:") # Output from visualize_similarity_matrix
visualize_similarity_matrix(words, similarity_matrix)Input matrix shape: (5, 3)
Input matrix:
[[0.2 0.8 0.3]
[0.7 0.2 0.9]
[0.3 0.5 0.2]
[0.1 0.3 0.4]
[0.8 0.1 0.6]]
Input matrix transpose:
[[0.2 0.7 0.3 0.1 0.8]
[0.8 0.2 0.5 0.3 0.1]
[0.3 0.9 0.2 0.4 0.6]]
Similarity matrix shape: (5, 5)
Similarity matrix:
time flies like an arrow
time [ 0.77][ 0.57][ 0.52][ 0.38][ 0.42]
flies [ 0.57][ 1.34][ 0.49][ 0.49][ 1.12]
like [ 0.52][ 0.49][ 0.38][ 0.26][ 0.41]
an [ 0.38][ 0.49][ 0.26][ 0.26][ 0.35]
arrow [ 0.42][ 1.12][ 0.41][ 0.35][ 1.01]Zum Beispiel ist der Wert des (1,2)-Elements der Ähnlichkeitsmatrix 0.57 die Vektordistanz (Ähnlichkeit) zwischen dem Wort “times” auf der x-Achse und dem Wort “flies” auf der y-Achse. Dies kann mathematisch wie folgt ausgedrückt werden.
- Die Matrix X der Wortsvektoren des Satzes
\(\mathbf{X} = \begin{bmatrix} \mathbf{x_1} \\ \mathbf{x_2} \\ \vdots \\ \mathbf{x_n} \end{bmatrix}\)
- Die transponierte Matrix von X
\(\mathbf{X}^T = \begin{bmatrix} \mathbf{x_1}^T & \mathbf{x_2}^T & \cdots & \mathbf{x_n}^T \end{bmatrix}\)
- Die Operation \(\mathbf{X}\mathbf{X}^T\)
\(\mathbf{X}\mathbf{X}^T = \begin{bmatrix} \mathbf{x_1} \cdot \mathbf{x_1} & \mathbf{x_1} \cdot \mathbf{x_2} & \cdots & \mathbf{x_1} \cdot \mathbf{x_n} \\ \mathbf{x_2} \cdot \mathbf{x_1} & \mathbf{x_2} \cdot \mathbf{x_2} & \cdots & \mathbf{x_2} \cdot \mathbf{x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{x_n} \cdot \mathbf{x_1} & \mathbf{x_n} \cdot \mathbf{x_2} & \cdots & \mathbf{x_n} \cdot \mathbf{x_n} \end{bmatrix}\)
- Jedes Element (i,j)
\((\mathbf{X}\mathbf{X}^T)_{ij} = \mathbf{x_i} \cdot \mathbf{x_j} = \sum_{k=1}^d x_{ik}x_{jk}\)
Jedes Element dieser n×n-Matrix ist das Skalarprodukt zweier Wortsvektoren und stellt daher die Distanz (Ähnlichkeit) zwischen zwei Wörtern dar. Dies sind die “Aufmerksamkeitswerte”.
Die folgende Schritt besteht darin, die Ähnlichkeitsmatrix in eine Gewichtsmatrix unter Verwendung des Softmax zu verwandeln. Dies ist der dritte Schritt.
Code
# 3. Convert similarities to weights (probability distribution) (softmax)
def softmax(x):
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True)) # trick for stability
return exp_x / exp_x.sum(axis=-1, keepdims=True)
attention_weights = softmax(similarity_matrix)
print("Attention weights shape:", attention_weights.shape)
print("Attention weights:\n", attention_weights)Attention weights shape: (5, 5)
Attention weights:
[[0.25130196 0.20574865 0.19571417 0.17014572 0.1770895 ]
[0.14838442 0.32047566 0.13697608 0.13697608 0.25718775]
[0.22189237 0.21533446 0.19290396 0.17109046 0.19877876]
[0.20573742 0.22966017 0.18247272 0.18247272 0.19965696]
[0.14836389 0.29876818 0.14688764 0.13833357 0.26764673]]Die Aufmerksamkeitsgewichte werden durch Anwendung der Softmax-Funktion berechnet. Dies führt zu zwei wesentlichen Transformationen:
- Ähnlichkeitswerte in Werte zwischen 0 und 1 umwandeln.
- Die Summe jeder Zeile auf 1 normieren, sodass sie eine Wahrscheinlichkeitsverteilung darstellen.
Die Umwandlung der Ähnlichkeitsmatrix in Gewichte ermöglicht es, die Relevanz von Wörtern zu anderen Wörtern in einer Wahrscheinlichkeit auszudrücken. Da sowohl Zeilen- als auch Spaltenachsen den Wortreihenfolge des Satzes entsprechen, stellt die erste Zeile der Gewichtsmatrix das Wortsatzzeichen für ‘time’ dar, und die Spalten repräsentieren alle Wörter im Satz. Folglich:
- Die Beziehungen zwischen allen anderen Wörtern (‘time’, ‘flies’, ‘like’, ‘an’, ‘arrow’) werden in Wahrscheinlichkeitswerten dargestellt.
- Die Summe dieser Wahrscheinlichkeitswerte ist 1.
- Hohe Wahrscheinlichkeitswerte deuten auf eine stärkere Relevanz hin.
Die so transformierten Gewichte werden im nächsten Schritt als Faktoren angewendet, um den Satz zu skalieren. Dabei zeigen diese Faktoren an, wie viel Information jedes Wort im Satz widerspiegelt. Dies entspricht der Entscheidung darüber, wie stark ein Wort die Informationen anderer Wörter “berücksichtigt”.
Code
# 4. Generate contextualized representations using the weights
contextualized_vectors = np.dot(attention_weights, X)
print("\nContextualized vectors shape:", contextualized_vectors.shape)
print("Contextualized vectors:\n", contextualized_vectors)
Contextualized vectors shape: (5, 3)
Contextualized vectors:
[[0.41168487 0.40880105 0.47401919]
[0.51455048 0.31810231 0.56944172]
[0.42911583 0.38823778 0.48665295]
[0.43462426 0.37646585 0.49769319]
[0.51082753 0.32015331 0.55869952]]Das Skalarprodukt der Gewichtsmatrix und der Wortmatrix (bestehend aus Wortvektoren) muss interpretiert werden. Angenommen, die erste Zeile von attention_weights ist [0.5, 0.2, 0.1, 0.1, 0.1], dann repräsentiert jeder Wert die Wahrscheinlichkeit der Relevanz von ‘time’ zu den anderen Wörtern. Die erste Gewichtszeile kann als \(\begin{bmatrix} \alpha_{11} & \alpha_{12} & \alpha_{13} & \alpha_{14} & \alpha_{15} \end{bmatrix}\) dargestellt werden, und die Operation der Wortmatrix mit dieser ersten Gewichtszeile kann wie folgt ausgedrückt werden.
\(\begin{bmatrix} \alpha_{11} & \alpha_{12} & \alpha_{13} & \alpha_{14} & \alpha_{15} \end{bmatrix} \begin{bmatrix} \vec{v}_{\text{time}} \ \vec{v}_{\text{flies}} \ \vec{v}_{\text{like}} \ \vec{v}_{\text{an}} \ \vec{v}_{\text{arrow}} \end{bmatrix}\)
Dies kann in Python-Code wie folgt dargestellt werden.
Code
time_contextualized = 0.5*time_vector + 0.2*flies_vector + 0.1*like_vector + 0.1*an_vector + 0.1*arrow_vector
# 0.5는 time과 time의 관련도 확률값
# 0.2는 time과 files의 관련도 확률값Die Operation multipliziert diese Wahrscheinlichkeiten (die Zeit ist mit jedem Wort assoziiert und repräsentiert die Wahrscheinlichkeitswerte) mit den ursprünglichen Vektoren jedes Worts und summiert sie auf. Das Ergebnis ist, dass der neue Vektor von ‘time’ ein gewichteter Mittelwert ist, der die Bedeutungen anderer Wörter in Abhängigkeit ihrer Relevanz widerspiegelt. Die Berechnung des gewichteten Mittelwerts ist entscheidend. Deshalb war es notwendig, in einem vorherigen Schritt die Gewichtsmatrix zu berechnen, um das gewichtete Mittel zu erhalten.
Die Shape des finalen kontextualisierten Vektors beträgt (5, 3), da dies das Ergebnis der Multiplikation der Aufmerksamkeitsgewichtsmatrix der Größe (5,5) mit der Wortsvektormatrix X der Größe (5,3) ist: (5,5) @ (5,3) = (5,3).
| Deutsch | Inhalt |
|---|---|
| Titel | Der aktuelle Stand der theoretischen Physik |
| Text | In den letzten Jahren ist die theoretische Physik rasch vorangegangen und es wurden wichtige Entdeckungen in verschiedenen Bereichen gemacht. |
8.2.3 Evolution zu Self-Attention
Das Google-Forschungsteam entdeckte einige Grenzen beim Analysieren des grundlegenden Aufmerksamkeitsmechanismus (Abschnitt 8.2.2). Das größte Problem war, dass die Wortevektoren gleichzeitig mehrere Aufgaben wie Ähnlichkeitsberechnung und Informationsübertragung uneffizient ausführen mussten. Zum Beispiel hat das Wort “bank” je nach Kontext verschiedene Bedeutungen, wie “Bank” oder “Ufer”, und sollte daher auch unterschiedliche Beziehungen zu anderen Wörtern haben. Allerdings war es schwierig, all diese verschiedenen Bedeutungen und Beziehungen mit einem einzigen Vektor auszudrücken.
Das Forschungsteam suchte nach einer Methode, um jede Rolle unabhängig zu optimieren. Dies war ähnlich wie das Entwickeln von Filtern in CNNs, die das Extrahieren von Merkmalen aus Bildern als lernfähige Form erweiterten. In der Aufmerksamkeit sollten spezialisierte Darstellungen für jede Rolle gelernt werden können. Diese Idee begann damit, Wortevektoren in Räume zu transformieren, die für verschiedene Rollen geeignet sind.
Grenzen des grundlegenden Konzepts (Code-Beispiel)
Code
def basic_self_attention(word_vectors):
similarity_matrix = np.dot(word_vectors, word_vectors.T)
attention_weights = softmax(similarity_matrix)
contextualized_vectors = np.dot(attention_weights, word_vectors)
return contextualized_vectorsIn dem obigen Code führt word_vectors gleichzeitig drei Aufgaben aus.
- Subjekt der Ähnlichkeitsberechnung: Es wird verwendet, um die Ähnlichkeit zu anderen Wörtern zu berechnen.
- Objekt der Ähnlichkeitsberechnung: Die Ähnlichkeit von anderen Wörtern wird an ihm berechnet.
- Informationstransfer: Es wird bei der Erstellung des finalen Kontextvektors zur Berechnung eines gewichteten Mittelwerts verwendet.
Erste Verbesserung: Trennung der Informationsübertragungsaufgabe
Das Forschungsteam trennte zunächst die Informationsübertragungsaufgabe. Die einfachste Methode, um in der linearen Algebra die Rolle von Vektoren zu trennen, besteht darin, Vektoren durch eine getrennte lernbare Matrix in einen neuen Raum zu linear transformieren (linear transformation).
Code
def improved_self_attention(word_vectors, W_similarity, W_content):
similarity_vectors = np.dot(word_vectors, W_similarity)
content_vectors = np.dot(word_vectors, W_content)
# Calculate similarity by taking the dot product between similarity_vectors
attention_scores = np.dot(similarity_vectors, similarity_vectors.T)
# Convert to probability distribution using softmax
attention_weights = softmax(attention_scores)
# Generate the final contextualized representation by multiplying weights and content_vectors
contextualized_vectors = np.dot(attention_weights, content_vectors)
return contextualized_vectorsW_similarity: eine lernbare Matrix, die Wortvektoren in einen Raum projiziert, der für die Berechnung von Ähnlichkeiten optimiert ist.W_content: eine lernbare Matrix, die Wortvektoren in einen Raum projiziert, der für die Informationsübermittlung optimiert ist.
Durch diese Verbesserung konnten similarity_vectors sich auf die Berechnung von Ähnlichkeiten und content_vectors auf die Informationsübermittlung spezialisieren. Dies bildete den Vorgänger des Konzepts, Information durch Value zu aggregieren.
Zweite Verbesserung: Vollständige Trennung der Ähnlichkeitsfunktion (Geburt von Q und K)
Der nächste Schritt war die Trennung des Prozesses zur Berechnung von Ähnlichkeiten in zwei Rollen. Anstatt dass similarity_vectors sowohl die Rolle des “Fragens” (Query) als auch die Rolle des “Antwortens” (Key) übernahmen, wurde diese beiden Funktionen vollständig getrennt.
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
class SelfAttention(nn.Module):
def __init__(self, embed_dim):
super().__init__()
# 각각의 역할을 위한 독립적인 선형 변환
self.q = nn.Linear(embed_dim, embed_dim) # 질문(Query)을 위한 변환
self.k = nn.Linear(embed_dim, embed_dim) # 답변(Key)을 위한 변환
self.v = nn.Linear(embed_dim, embed_dim) # 정보 전달(Value)을 위한 변환
def forward(self, x):
Q = self.q(x) # 질문자로서의 표현
K = self.k(x) # 응답자로서의 표현
V = self.v(x) # 전달할 정보의 표현
# 질문과 답변 간의 관련성(유사도) 계산
scores = torch.matmul(Q, K.transpose(-2, -1))
weights = F.softmax(scores, dim=-1)
# 관련성에 따른 정보 집계 (가중 평균)
return torch.matmul(weights, V)Bedeutung der Trennung der Q, K, V-Räume
Die Reihenfolge von Q und K kann vertauscht werden (\(QK^T\) anstelle von \(KQ^T\)), und mathematisch erhalten wir die gleiche Ähnlichkeitsmatrix. Aus rein mathematischer Sicht sind diese beiden gleich, aber warum wurden sie als “Abfrage (Query)” und “Schlüssel (Key)” benannt? Der Kern liegt darin, für eine bessere Berechnung der Ähnlichkeit getrennte Räume zu optimieren. Diese Bezeichnungen scheinen darauf hinzudeuten, dass die Aufmerksamkeitsmechanismen im Transformer-Modell von Informationsabrufsystemen inspiriert wurden. In Suchsystemen ist eine “Abfrage (Query)” das, was der Benutzer sucht, und ein “Schlüssel (Key)” ähnelt den Indextermen in Dokumenten. Die Aufmerksamkeit imitiert den Prozess, bei dem die Ähnlichkeit zwischen Abfrage und Schlüsseln berechnet wird, um relevante Informationen zu finden.
Beispielsweise:
- “I need to deposit money in the bank” (Bank)
- “The river bank is covered with flowers” (Ufer)
In den obigen beiden Sätzen hat “bank” je nach Kontext verschiedene Bedeutungen. Durch die Trennung der Q, K-Räume
- werden “bank” und andere Wörter in den Q, K-Räumen auf unterschiedliche Weise positioniert, um die Ähnlichkeitsberechnung zu optimieren.
- In einem finanzbezogenen Kontext werden Vektoren so angeordnet, dass die Ähnlichkeit mit ‘money’, ‘deposit’ usw. erhöht wird.
- In einem geografisch orientierten Kontext werden sie so positioniert, dass die Ähnlichkeit mit ‘river’, ‘covered’ usw. erhöht wird.
Mit anderen Worten bedeutet das Q-K-Paar das Skalarprodukt in zwei optimierten Räumen, um die Ähnlichkeit zu berechnen. Ein wichtiger Punkt ist, dass der Q- und K-Raum durch das Lernen optimiert werden. Es ist sehr wahrscheinlich, dass das Google-Forschungsteam entdeckt hat, dass die Matrizen Q und K während des Lernprozesses tatsächlich so optimiert wurden, dass sie ähnlich wie Abfrage und Schlüssel funktionieren.
Bedeutung der Trennung der Q, K-Räume
Ein weiterer Vorteil, den man durch die Trennung von Q und K erzielt, ist Flexibilität. Wenn Q und K in demselben Raum liegen, kann die Art der Ähnlichkeitsberechnung eingeschränkt sein (z.B. symmetrische Ähnlichkeit). Durch die Trennung von Q und K können jedoch komplexere und asymmetrischere Beziehungen (z.B. “A ist die Ursache von B”) gelernt werden. Darüber hinaus ermöglichen unterschiedliche Transformationen (\(W^Q\), \(W^K\)) eine detailliertere Darstellung der Rolle jedes Worts, was die Ausdrucksfähigkeit des Modells erhöht. Schließlich führt die Trennung von Q- und K-Räumen zu klareren Optimierungsziele für jeden Raum: Q und K optimieren die Art, wie Informationen gefunden werden, während V den Inhalt der übermittelten Informationen übernimmt.
Mathematische Darstellung der Aufmerksamkeit
Der endgültige Aufmerksamkeitsmechanismus wird durch die folgende Formel dargestellt:
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\] * \(Q \in \mathbb{R}^{n \times d_k}\): Abfrage-Matrix * \(K \in \mathbb{R}^{n \times d_k}\): Schlüssel-Matrix * \(V \in \mathbb{R}^{n \times d_v}\): Wert-Matrix (\(d_v\) ist in der Regel gleich \(d_k\)) * \(n\): Sequenzlänge * \(d_k\): Dimension der Abfrage-, Schlüssel-Vektoren * \(d_v\): Dimension des Wertvektors * \(\frac{QK^T}{\sqrt{d_k}}\): Scaled Dot-Product Attention. Mit zunehmender Dimension wachsen die Skalarprodukte, um das Verschwinden von Gradienten bei der Verarbeitung durch die Softmax-Funktion zu verhindern.
Diese fortschrittliche Struktur wurde zum Kernbestandteil der Transformer und bildete die Grundlage moderner Sprachmodelle wie BERT und GPT.
Klicken Sie hier, um den Inhalt anzuzeigen (Theorie-Tiefgang: Integrierte Understanding und aktuelle Theorien des Selbst-Aufmerksamkeitsmechanismus)
Integrierte Auffassung und aktuelle Theorien des Selbst-Attention-Mechanismus
1. Mathematische Prinzipien und Berechnungskomplexität
Selbst-Attention berechnet für jedes Wort in der Eingabesequenz dessen Beziehung zu allen anderen Wörtern, einschließlich sich selbst, um einen neuen Kontext reflektierenden Vektor zu erzeugen. Dieser Prozess besteht aus drei Hauptphasen.
Erstellung von Query, Key und Value:
Für jeden Einbettungsvektor (\(x_i\)) eines Worts in der Eingabesequenz werden drei lineare Transformationen angewendet, um die Vektoren Query (\(q_i\)), Key (\(k_i\)) und Value (\(v_i\)) zu erstellen. Diese Transformationen werden mit lernfähigen Gewichtsmatrizen (\(W^Q\), \(W^K\), \(W^V\)) durchgeführt.
\(q_i = x_i W^Q\)
\(k_i = x_i W^K\)
\(v_i = x_i W^V\)
\(W^Q, W^K, W^V \in \mathbb{R}^{d_{model} \times d_k}\): Lernfähige Gewichtsmatrizen. (\(d_{model}\): Einbettungsdimension, \(d_k\): Dimension der Query-, Key- und Value-Vektoren)
Berechnung und Normalisierung der Attention-Scores
Für jedes Wortpaar wird das Skalarprodukt (dot product) von Query- und Key-Vektoren berechnet, um den Attention-Score zu erhalten.
\[\text{score}(q_i, k_j) = q_i \cdot k_j^T\]
Dieser Score zeigt an, wie stark zwei Wörter miteinander verbunden sind. Nach der Berechnung des Skalarprodukts wird eine Skalierung (scaling) durchgeführt, um zu verhindern, dass die Skalarproduktwerte zu groß werden und so das Problem des Gradientenverschwindens (gradient vanishing) zu mildern. Die Skalierung erfolgt durch Division durch die Quadratwurzel der Dimension des Key-Vektors (\(d_k\)).
\[\text{scaled score}(q_i, k_j) = \frac{q_i \cdot k_j^T}{\sqrt{d_k}}\]
Schließlich wird die Softmax-Funktion angewendet, um die Attention-Scores zu normalisieren und so die Attention-Gewichte für jedes Wort zu erhalten.
\[\alpha_{ij} = \text{softmax}(\text{scaled score}(q_i, k_j)) = \frac{\exp(\text{scaled score}(q_i, k_j))}{\sum_{l=1}^{n} \exp(\text{scaled score}(q_i, k_l))}\]
Hierbei ist \(\alpha_{ij}\) das Attention-Gewicht, das das \(i\)-te Wort dem \(j\)-ten Wort zuweist, und \(n\) ist die Länge der Sequenz.
Berechnung des gewichteten Mittelwerts
Die Attention-Gewichte (\(\alpha_{ij}\)) werden verwendet, um den gewichteten Mittelwert (weighted average) der Value-Vektoren (\(v_j\)) zu berechnen. Dieser gewichtete Mittelwert wird zu einem Kontextvektor \(c_i\), der Informationen aller Wörter in der Eingabesequenz zusammenfasst.
\[c_i = \sum_{j=1}^{n} \alpha_{ij} v_j\]
Darstellung des gesamten Prozesses in Matrixform
Für eine Einbettungsmatrix \(X \in \mathbb{R}^{n \times d_{model}}\) kann der gesamte Selbst-Attention-Prozess wie folgt dargestellt werden.
\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]
Hierbei ist \(Q = XW^Q\), \(K = XW^K\), und \(V = XW^V\).
Berechnungskomplexität
Die Berechnungskomplexität von Selbst-Attention ist \(O(n^2)\) in Bezug auf die Länge der Eingabesequenz (\(n\)). Dies liegt daran, dass für jedes Wort die Beziehung zu allen anderen Wörtern berechnet werden muss. * \(QK^T\)-Berechnung: Da \(n\) Abfragevektoren und \(n\) Schlüsselvektoren miteinander skalar multipliziert werden, ist eine Berechnung der Komplexität \(O(n^2d_k)\) erforderlich. * Softmax-Berechnung: Um die Aufmerksamkeitsgewichte für jede Abfrage zu berechnen, wird die Softmax-Funktion auf die \(n\) Schlüssel angewendet, was eine Berechnungszeit von \(O(n^2)\) erfordert. * Gewichteter Mittelwert mit \(V\): Da \(n\) Value-Vektoren und \(n\) Aufmerksamkeitsgewichte multipliziert werden müssen, ist die Berechnungskomplexität \(O(n^2d_k)\).
2. Erweiterung aus der Sicht der Kernel-Maschinen
2.1 Asymmetrische Kernelfunktionen
Interpretation von Aufmerksamkeit als asymmetrische Kernelfunktion \(K(Q_i, K_j) = \exp\left(\frac{Q_i \cdot K_j}{\sqrt{d_k}}\right)\)
Dieser Kernel lernt eine Merkmalsabbildung, die den Eingaberaum umstrukturiert.
2.2 Singularwertzerlegungs-Analyse (SVD)
Asymmetrische KSVD der Aufmerksamkeitsmatrix
\(A = U\Sigma V^T \quad \text{wobei } \Sigma = \text{diag}(\sigma_1, \sigma_2, ...)\)
-\(U\): Hauptsrichtungen im Abfrageraum (Muster von Kontextanforderungen) -\(V\): Hauptsrichtungen im Schlüsselraum (Informationsbereitstellungs-Muster) -\(\sigma_i\): Interaktionsstärke (Beobachtung eines Konzentrationsphänomens mit ≥0.9 Erklärungskraft)
3. Energiemodellierung und Dynamik
3.1 Formulierung der Energiefunktion
\(E(Q,K,V) = -\sum_{i,j} \frac{Q_i \cdot K_j}{\sqrt{d_k}}V_j + \text{Log-Partitionsfunktion}\)
Die Ausgabe wird als Prozess der Energieminimierung interpretiert
\(\text{Output} = \arg\min_V E(Q,K,V)\)
3.2 Äquivalenz zu Hopfield-Netzen
Gleichungen für kontinuierliche Hopfield-Netze
\(\mathcal{F}(A)_{kl} = \sum_{m,n} A_{mn}e^{-i2\pi(mk/M+nl/N)}\)
Niedrige Frequenzkomponenten fangen über 80% der Information ein.
6. Informations-theoretische Interpretation
6.1 Maximierung der gegenseitigen Information
\(\max I(X;Y) = H(Y) - H(Y|X) \quad \text{u.d.N. } Y = \text{Aufmerksamkeit}(X)\)
Softmax generiert die optimale Verteilung, die Entropie \(H(Y)\) maximiert.
6.2 Signal-to-Noise Ratio (SNR)-Analyse
SNR-Dämpfung in Abhängigkeit der Schichttiefe \(l\)
\(\text{SNR}^{(l)} \propto e^{-0.2l} \quad \text{(basierend auf ResNet-50)}\)
7. Neurobiologische Inspiration
7.1 Visuelles Cortical-Areal V4
- Richtungsselektive Neuronen ≈ Aufmerksamkeitsköpfe, die auf bestimmte Muster reagieren
- Hierarchische Rezeptorfeldstruktur ≈ Multiskalen-Aufmerksamkeit
7.2 Vorfrontallärm-Arbeitsgedächtnis
- Persistente neuronale Aktivierung ≈ Verarbeitung von langfristigen Abhängigkeiten in der Aufmerksamkeit
- Kontextbeibehaltungsmechanismus ≈ Maskierungstechniken im Decoder
8. Erweiterte mathematische Modellierung
8.1 Tensor-Netzwerk-Erweiterung
MPO (Matrix Product Operator) Darstellung
\(A_{ij} = \sum_{\alpha=1}^r Q_{i\alpha}K_{j\alpha}\) Hierbei ist \(r\) die Bindungsdimension des Tensor-Netzwerks.
8.2 Differentialgeometrische Analyse
Riemannsche Krümmung der Aufmerksamkeitsmannigfaltigkeit \(R_{ijkl} = \partial_i\Gamma_{jk}^m - \partial_j\Gamma_{ik}^m + \Gamma_{il}^m\Gamma_{jk}^l - \Gamma_{jl}^m\Gamma_{ik}^l\)
Durch die Krümmungsanalyse kann man die Grenzen der Ausdrucksstärke des Modells schätzen.
9. Aktuelle Forschungstrends (2025)
Quanten-Aufmerksamkeit
- Darstellung von Abfrage/Schlüssel als Quantensuperposition: \(|\psi_Q\rangle = \sum c_i|i\rangle\)
- Beschleunigung der Quanten-Skalarprodukts-Operation
Bioinspirierte Optimierung
- Anwendung von spike-timing-dependent plasticity (STDP)
\(\Delta W_{ij} \propto x_i x_j - \beta W_{ij}\)
Dynamische Energieanpassung
- Echtzeit-Anpassung der Energiestarre durch Meta-Lernen
- Simulation durch Kopplung mit physikalischen Motoren
Literatur
- Vaswani et al., “Attention Is All You Need”, NeurIPS 2017
- Choromanski et al., “Rethinking Attention with Performers”, ICLR 2021
- Ramsauer et al., “Hopfield Networks is All You Need”, ICLR 2021
- Wang et al., “Linformer: Self-Attention with Linear Complexity”, arXiv 2020
- Chen et al., “Theoretical Analysis of Self-Attention via Signal Propagation”, NeurIPS 2023
8.2.4 Multi-Head Attention und parallele Verarbeitung
Das Forschungsteam von Google kam auf die Idee, dass es besser sein könnte, “anstelle eines großen Aufmerksamkeitsraums mehrere kleinere Aufmerksamkeitsräume zu verwenden, um verschiedene Arten von Beziehungen zu erfassen.” Ähnlich wie mehrere Experten ein Problem aus verschiedenen Perspektiven analysieren, könnten unterschiedliche Aspekte der Eingabe-Sequenz gleichzeitig berücksichtigt werden, um reichhaltigere Kontextinformationen zu erhalten.
Basierend auf dieser Idee entwickelten die Forscher das Multi-Head Attention, bei dem Q-, K- und V-Vektoren in mehrere kleinere Räume aufgeteilt werden, um die Aufmerksamkeit parallell zu berechnen. Im ursprünglichen Paper (“Attention is All You Need”) wurde ein 512-dimensionaler Embedding in acht 64-dimensionale Köpfe (heads) unterteilt. Spätere Modelle wie BERT erweiterten diese Struktur weiter (z.B. BERT-base teilt eine 768-dimensionale Ebene in 12 64-dimensionale Köpfe).
Funktionsweise des Multi-Head Attention
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
class MultiHeadAttention(nn.Module):
def __init__(self, config):
super().__init__()
assert config.hidden_size % config.num_attention_heads == 0
self.d_k = config.hidden_size // config.num_attention_heads # Dimension of each head
self.h = config.num_attention_heads # Number of heads
# Linear transformation layers for Q, K, V, and output
self.linear_layers = nn.ModuleList([
nn.Linear(config.hidden_size, config.hidden_size)
for _ in range(4) # For Q, K, V, and output
])
self.dropout = nn.Dropout(config.attention_probs_dropout_prob) # added
self.attention_weights = None # added
def attention(self, query, key, value, mask=None): # separate function
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(self.d_k) # scaled dot product
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
self.attention_weights = p_attn.detach() # Store attention weights
p_attn = self.dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
def forward(self, query, key, value, mask=None):
batch_size = query.size(0)
# 1) Linear projections in batch from d_model => h x d_k
query, key, value = [l(x).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linear_layers, (query, key, value))]
# 2) Apply attention on all the projected vectors in batch.
x, attn = self.attention(query, key, value, mask=mask)
# 3) "Concat" using a view and apply a final linear.
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.h * self.d_k)
return self.linear_layers[-1](x)Multikopf-Attention (Multi-Head Attention) detaillierte Analyse
Code-Struktur (__init__ und forward)
Der Code für die Multikopf-Attention besteht hauptsächlich aus der Initialisierungsmethode (__init__) und der Vorwärtspropagationsmethode (forward). Wir werden uns die Rolle und die detaillierten Abläufe jeder Methode genauer ansehen.
__init__-Methode:d_k: Dies zeigt die Dimension jedes Attention-Kopfes an. Dieser Wert ist das Ergebnis der Division der Hidden Size des Modells durch die Anzahl der Aufmerksamkeitsköpfe (num_attention_heads) und bestimmt die Menge an Informationen, die jeder Kopf verarbeitet.h: Setzt die Anzahl der Attention-Kopfes. Dieser Wert ist ein Hyperparameter, der bestimmt, aus wie vielen verschiedenen Perspektiven das Modell auf die Eingabe schaut.linear_layers: Erstellt insgesamt vier lineare Transformationslayer für Query (Q), Key (K), Value (V) und die finale Ausgabe. Diese Layer transformieren die Eingaben für jeden Kopf und integrieren am Ende die Ergebnisse der Köpfe.
forward-Methode:- Lineare Transformation und Aufteilung:
- Für
query,keyundvalue, die als Eingabe erhalten werden, wird jeweilsself.linear_layersverwendet, um eine lineare Transformation durchzuführen. Dies transformiert die Eingaben in ein Format, das für jeden Kopf geeignet ist. - Die
view-Funktion wird verwendet, um die Form des Tensors von (batch_size, sequence_length, hidden_size) zu (batch_size, sequence_length, h, d_k) zu ändern. Dies verteilt die gesamte Eingabe auf h Kopfes. - Mit der
transpose-Funktion wird die Dimension des Tensors von (batch_size, sequence_length, h, d_k) zu (batch_size, h, sequence_length, d_k) geändert. Nun sind die einzelnen Köpfe bereit, die Attention-Berechnungen unabhängig voneinander durchzuführen.
- Für
- Anwendung der Attention:
- Für jeden Kopf wird die
attention-Funktion aufgerufen, also die Skalierte Dot-Product Attention, um die Attention-Gewichte und das Ergebnis jedes Kopfs zu berechnen.
- Für jeden Kopf wird die
- Kombinieren und finale lineare Transformation:
- Die
transpose- undcontiguous-Funktionen werden verwendet, um die Ergebnisse (x) jedes Kopfes wieder in die Form (batch_size, sequence_length, h, d_k) zurückzuwandeln. - Die
view-Funktion wird verwendet, um die Struktur auf (batch_size, sequence_length, h * d_k), also (batch_size, sequence_length, hidden_size) zu integrieren. - Schließlich wird
self.linear_layers[-1]angewendet, um die finale Ausgabe zu erzeugen. Diese lineare Transformation fasst die Ergebnisse der Köpfe zusammen und erzeugt letztendlich eine Ausgabe in der von dem Modell gewünschten Form.
- Die
- Lineare Transformation und Aufteilung:
attention-Methode (Skalierte Dot-Product Attention):- Diese Funktion ist der Ort, an dem tatsächlich das Attention-Mechanismus für jeden Kopf ausgeführt wird, und gibt die Ergebnisse jedes Kopfs und die Attention-Gewichte zurück.
- Kernpunkt: Beim Berechnen von
scoresist es sehr wichtig, dass durch die Quadratwurzel der Dimension deskey-Vektors (\(\sqrt{d_k}\)) skaliert wird.- Zweck: Dies verhindert, dass die Werte des Skalarprodukts (\(QK^T\)) mit wachsender Größe zu stark ansteigen und somit die Eingaben der Softmax-Funktion übermäßig groß werden. Dies mildert das Problem des Gradientenverschwindens (gradient vanishing) und stabilisiert das Lernen, was wiederum zur Verbesserung der Modellleistung beiträgt.
Die Rolle jedes Kopfes und die Vorteile der Multikopf-Attention Multikopf-Aufmerksamkeit ist vergleichbar mit dem Betrachten eines Objekts durch mehrere “kleine Linse” aus verschiedenen Winkeln. Jeder Kopf transformiert unabhängig Abfragen (Q), Schlüssel (K) und Werte (V) und führt Aufmerksamkeitsberechnungen durch. Dies ermöglicht es, sich auf verschiedene Teilräume (subspace) innerhalb der gesamten Eingangsequenz zu konzentrieren und Informationen zu extrahieren.
- Verschiedene Beziehungen erfassen: Jeder Kopf kann spezialisiert sein auf das Lernen verschiedener Arten linguistischer Beziehungen. Zum Beispiel kann ein Kopf sich auf Subjekt-Prädikat-Beziehungen konzentrieren, während ein anderer auf Adjektiv-Nomen-Beziehungen und noch einer auf die Beziehung zwischen Pronomen und ihren Antezedenten.
- Recheneffizienz: Jeder Kopf berechnet Aufmerksamkeit in einem relativ kleinen Raum (d_k). Dies ist rechnerisch effizienter als das Berechnen der Aufmerksamkeit in einem großen Raum.
- Parallele Verarbeitung: Die Berechnungen jedes Kopfs sind voneinander unabhängig. Daher ist parallele Verarbeitung unter Nutzung von GPU möglich, was die Rechengeschwindigkeit erheblich erhöht.
Praktische Analysebeispiele
Studien zeigen, dass die einzelnen Köpfe der Multikopf-Aufmerksamkeit tatsächlich verschiedene linguistische Merkmale erfassen. Zum Beispiel enthüllt die Analyse der Multikopf-Aufmerksamkeit des BERT-Modells in dem Artikel “What does BERT Look At? An Analysis of BERT’s Attention”, dass einige Köpfe wichtig für das Verstehen der syntaktischen Struktur von Sätzen sind, während andere wichtiger für die Erkennung semantischer Ähnlichkeiten zwischen Wörtern sind.
Mathematische Darstellung
- Gesamt: \(\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O\)
- Jeder Kopf: \(\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)\)
- Aufmerksamkeitsfunktion: \(\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\)
Notationsklärung:
- \(h\): Anzahl der Köpfe
- \(W_i^Q \in \mathbb{R}^{d_{\text{model}} \times d_k}\): Transformationsmatrix für die Abfrage des i-ten Kopfes
- \(W_i^K \in \mathbb{R}^{d_{\text{model}} \times d_k}\): Transformationsmatrix für den Schlüssel des i-ten Kopfes
- \(W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_v}\): Transformationsmatrix für den Wert des i-ten Kopfes
- \(W^O \in \mathbb{R}^{h \cdot d_v \times d_{\text{model}}}\): Lineare Transformationsmatrix zur Erzeugung der finalen Ausgabe
Bedeutung der finalen linearen Transformation (\(W^O\)): Die zusätzliche lineare Transformation (\(W^O\)), die nach dem einfachen Verbinden (Concat) der Ausgaben der einzelnen Köpfe durchgeführt wird, um die ursprüngliche Einbettungsdimension (\(d_{model}\)) wiederherzustellen, spielt eine sehr wichtige Rolle.
- Informationen integrieren: Sie integriert die verschiedenen Perspektiven, die von den verschiedenen Köpfen extrahiert wurden, in einer ausgewogen und stabilen Weise, um reichhaltige Kontextinformationen insgesamt darzustellen.
- Optimale Kombination: Im Lernprozess lernt sie selbstständig, wie die Informationen der einzelnen Köpfe am effektivsten kombiniert werden. Dies ist vergleichbar mit dem Prinzip, bei dem in einem Ensemble-Modell nicht einfach die Vorhersagen der einzelnen Modelle durchschnittlich gebildet werden, sondern durch gelernte Gewichte kombiniert werden.
Zusammenfassung
Multikopf-Aufmerksamkeit ist ein Mechanismus, der es den Transformer-Modellen ermöglicht, kontextuelle Informationen aus Eingangsequenzen effizient zu erfassen und durch die Nutzung von GPU die Rechengeschwindigkeit zu erhöhen. Dadurch zeigen Transformatoren in verschiedenen NLP-Aufgaben hervorragende Leistungen.
8.2.5 Maskierungsstrategien für paralleles Lernen
Nach der Implementierung von Multi-Head Attention stießen die Forscherteams auf ein wichtiges Problem während des tatsächlichen Trainingsprozesses. Es handelte sich um das Phänomen, dass das Modell zukünftige Wörter zur Vorhersage aktueller Wörter referenziert, auch als “Informationsverschleppung (information leakage)” bezeichnet. Zum Beispiel bei dem Satz “The cat ___ on the mat”, konnte das Modell leicht “sits” vorhersagen, indem es voraussah, dass “mat” später kommt.
Notwendigkeit von Maskierung: Verhindern von Informationsverschleppung
Diese Informationsverschleppung führt dazu, dass das Modell nicht seine tatsächliche Inferenzfähigkeit entwickelt, sondern lediglich die richtige Antwort “errät”. Obwohl das Modell während des Trainings hochwertige Leistungen zeigt, ist es bei neuen Daten (zukünftigen Zeitpunkten) nicht in der Lage, angemessen zuvorzusagen.
Um dieses Problem zu lösen, führten die Forscher eine sorgfältig entwickelte Maskierungsstrategie (masking) ein. In Transformers werden zwei Arten von Masken verwendet:
- Kausalitätsmaske (Causal Mask, Look-Ahead Mask): Verhindert in autoregressiven Modellen, dass zukünftige Informationen referenziert werden.
- Padding-Maske (Padding Mask): Entfernt den Einfluss sinnloser Padding-Tokens (padding token) bei der Verarbeitung von variabler Länge-Sequenzen.
1. Kausalitätsmaske (Causal Mask)
Die Kausalitätsmaske hat die Aufgabe, zukünftige Informationen zu verbergen. Durch die Ausführung des folgenden Codes kann man visuell erkennen, wie Teile der Aufmerksamkeitscore-Matrix, die zukünftigen Informationen entsprechen, gemaskiert werden.
Code
from dldna.chapter_08.visualize_masking import visualize_causal_mask
visualize_causal_mask()1. Original attention score matrix:
I love deep learning
I [ 0.90][ 0.70][ 0.30][ 0.20]
love [ 0.60][ 0.80][ 0.90][ 0.40]
deep [ 0.20][ 0.50][ 0.70][ 0.90]
learning [ 0.40][ 0.30][ 0.80][ 0.60]
Each row represents the attention scores from the current position to all positions
--------------------------------------------------
2. Lower triangular mask (1: allowed, 0: blocked):
I love deep learning
I [ 1.00][ 0.00][ 0.00][ 0.00]
love [ 1.00][ 1.00][ 0.00][ 0.00]
deep [ 1.00][ 1.00][ 1.00][ 0.00]
learning [ 1.00][ 1.00][ 1.00][ 1.00]
Only the diagonal and below are 1, the rest are 0
--------------------------------------------------
3. Mask converted to -inf:
I love deep learning
I [ 1.0e+00][ -inf][ -inf][ -inf]
love [ 1.0e+00][ 1.0e+00][ -inf][ -inf]
deep [ 1.0e+00][ 1.0e+00][ 1.0e+00][ -inf]
learning [ 1.0e+00][ 1.0e+00][ 1.0e+00][ 1.0e+00]
Converting 0 to -inf so that it becomes 0 after softmax
--------------------------------------------------
4. Attention scores with mask applied:
I love deep learning
I [ 1.9][ -inf][ -inf][ -inf]
love [ 1.6][ 1.8][ -inf][ -inf]
deep [ 1.2][ 1.5][ 1.7][ -inf]
learning [ 1.4][ 1.3][ 1.8][ 1.6]
Future information (upper triangle) is masked with -inf
--------------------------------------------------
5. Final attention weights (after softmax):
I love deep learning
I [ 1.00][ 0.00][ 0.00][ 0.00]
love [ 0.45][ 0.55][ 0.00][ 0.00]
deep [ 0.25][ 0.34][ 0.41][ 0.00]
learning [ 0.22][ 0.20][ 0.32][ 0.26]
The sum of each row becomes 1, and future information is masked to 0Sequenzverarbeitungsarchitektur und Matrizen
Um zu erklären, warum zukünftige Informationen die Form einer oberen Dreiecksmatrix annehmen, werde ich das Beispiel des Satzes “I love deep learning” verwenden. Die Wortreihenfolge lautet [I(0), love(1), deep(2), learning(3)]. In der Aufmerksamkeitspunktmatrix(\(QK^T\)) folgen sowohl die Zeilen als auch die Spalten dieser Wortreihenfolge.
Code
attention_scores = [
[0.9, 0.7, 0.3, 0.2], # I -> I, love, deep, learning
[0.6, 0.8, 0.9, 0.4], # love -> I, love, deep, learning
[0.2, 0.5, 0.7, 0.9], # deep -> I, love, deep, learning
[0.4, 0.3, 0.8, 0.6] # learning -> I, love, deep, learning
]- Jede Zeile von Q ist der Abfravektor des aktuell verarbeiteten Worts.
- Jede Spalte von K (da K transponiert wurde) ist der Schlüsselvektor des referenzierten Wortes.
Die Interpretation der Matrizen:
- Zeile (I): [I] → [I, love, deep, learning] in Beziehung
- Zeile (love): [love] → [I, love, deep, learning] in Beziehung
- Zeile (deep): [deep] → [I, love, deep, learning] in Beziehung
- Zeile (learning): [learning] → [I, love, deep, learning] in Beziehung
Beim Verarbeiten des Wortes “deep” (3. Zeile)
- verfügbare Referenz: [I, love, deep] (Wörter, die bisher aufgetreten sind)
- nicht verfügbare Referenz: [learning] (Wort, das noch nicht erschienen ist)
Daher, wenn man sich auf die Zeilen konzentriert, werden die zukünftigen Wörter des entsprechenden Spaltenwortes (zukünftige Informationen) der Teil rechts von dieser Position, also der oberdreieckige (upper triangular) Teil. Umgekehrt sind die verfügbaren Referenzwörter der untere Dreieck (lower triangular) Teil.
Die Kausalitätsmaske setzt den unteren Dreiecksteil auf 1 und den oberen Dreiecksteil auf 0, wobei die 0 des oberen Dreiecks durch \(-\infty\) ersetzt werden. 2. \(-\infty\) wird bei Durchlauf der Softmax-Funktion zu 0. Die Maske-Matrix wird einfach zur Aufmerksamkeitspunktzahlsmatrix addiert. Das Ergebnis ist, dass in der Matrix der auf die Softmax-Funktion angewendeten Aufmerksamkeitspunktzahlen die zukünftige Information durch 0 blockiert wird.
2. Padding-Maske (Padding Mask)
In der natürlichen Sprachverarbeitung variieren die Satzlängen. Für den Batch-Verarbeitungsbedarf müssen alle Sätze auf die gleiche Länge angepasst werden, wobei kurze Sätze mit Padding-Token (PAD) aufgefüllt werden. Diese Padding-Tokens sind jedoch semantisch bedeutungslos und dürfen daher nicht in die Aufmerksamkeitsberechnung einbezogen werden.
Code
from dldna.chapter_08.visualize_masking import visualize_padding_mask
visualize_padding_mask()
2. Create padding mask (1: valid token, 0: padding token):
tensor([[[1., 1., 1., 1.]],
[[1., 1., 1., 0.]],
[[1., 1., 1., 1.]],
[[1., 1., 1., 1.]]])
Positions that are not padding (0) are 1, padding positions are 0
--------------------------------------------------
3. Original attention scores (first sentence):
I love deep learning
I [ 0.90][ 0.70][ 0.30][ 0.20]
love [ 0.60][ 0.80][ 0.90][ 0.40]
deep [ 0.20][ 0.50][ 0.70][ 0.90]
learning [ 0.40][ 0.30][ 0.80][ 0.60]
Attention scores at each position
--------------------------------------------------
4. Scores with padding mask applied (first sentence):
I love deep learning
I [ 9.0e-01][ 7.0e-01][ 3.0e-01][ 2.0e-01]
love [ 6.0e-01][ 8.0e-01][ 9.0e-01][ 4.0e-01]
deep [ 2.0e-01][ 5.0e-01][ 7.0e-01][ 9.0e-01]
learning [ 4.0e-01][ 3.0e-01][ 8.0e-01][ 6.0e-01]
The scores at padding positions are masked with -inf
--------------------------------------------------
5. Final attention weights (first sentence):
I love deep learning
I [ 0.35][ 0.29][ 0.19][ 0.17]
love [ 0.23][ 0.28][ 0.31][ 0.19]
deep [ 0.17][ 0.22][ 0.27][ 0.33]
learning [ 0.22][ 0.20][ 0.32][ 0.26]
The weights at padding positions become 0, and the sum of the weights at the remaining positions is 1Wir werden die folgenden Sätze als Beispiel verwenden.
- “I love ML” → [I, love, ML, PAD]
- “Deep learning is fun” → [Deep, learning, is, fun]
Hier wurde der erste Satz aufgrund der drei Wörter am Ende mit PAD aufgefüllt. Die Padding-Maske entfernt den Einfluss dieser PAD-Token. Sie erzeugt eine Maske, die echte Wörter als 1 und Padding-Token als 0 kennzeichnet, und 2. setzt die Aufmerksamkeitsscores an den Padding-Positionen auf \(-\infty\), sodass sie nach dem Softmax-Durchgang zu 0 werden.
Dadurch erzielen wir folgende Effekte:
- Die echten Wörter können sich gegenseitig frei Aufmerksamkeit schenken.
- Die Padding-Token werden komplett aus den Aufmerksamkeitsberechnungen ausgeschlossen.
- Der Kontext wird nur durch die tatsächlich bedeutenden Teile jedes Satzes gebildet.
Code
def create_attention_mask(size):
# Create a lower triangular matrix (including the diagonal)
mask = torch.tril(torch.ones(size, size))
# Mask with -inf (becomes 0 after softmax)
mask = mask.masked_fill(mask == 0, float('-inf'))
return mask
def masked_attention(Q, K, V, mask):
# Calculate attention scores
scores = torch.matmul(Q, K.transpose(-2, -1))
# Apply mask
scores = scores + mask
# Apply softmax
weights = F.softmax(scores, dim=-1)
# Calculate final attention output
return torch.matmul(weights, V)Innovation und Auswirkungen der Maskierungstrategien
Die beiden von dem Forschungsteam entwickelten Maskierungstrategien (Padding-Mask, Causal-Mask) haben den Lernprozess der Transformer robuster gemacht und bildeten die Grundlage für später autoregressive Modelle wie GPT. Insbesondere die Causal-Mask hat das Sprachmodell dazu angeregt, Kontext in einer sequenziellen Weise zu erfassen, die dem tatsächlichen Verständnis von menschlicher Sprache ähnelt.
Effizienz der Implementierung
Die Maskierung wird direkt nach der Berechnung der Aufmerksamkeitswerte und vor der Anwendung der Softmax-Funktion durchgeführt. Positionen, die mit \(-\infty\) maskiert sind, werden beim Durchlaufen der Softmax-Funktion zu 0, wodurch die Information an diesen Positionen vollständig blockiert wird. Dies ist auch aus Sicht von Rechen- und Speichereffizienz eine optimierte Herangehensweise.
Durch die Einführung dieser Maskierungstrategien wurde es dem Transformer ermöglicht, truly paralleles Lernen zu realisieren, was einen großen Einfluss auf die Entwicklung moderner Sprachmodelle hatte.
8.2.6 Entwicklung der Bedeutung von “Head”: Von “Kopf” zu “Gehirn”
Im Deep Learning hat sich die Bedeutung des Begriffs “Head” mit der Entwicklung von neuronalen Netzarchitekturen allmählich und grundlegend verändert. Anfangs wurde er in der Regel im Vergleich einfach als “Teil, der dem Ausgabeschicht näher ist”, verwendet, während er sich in jüngerer Zeit zu einer abstrakteren und komplexeren Bedeutung als “unabhängiges Modul, das eine bestimmte Funktion des Modells übernimmt” entwickelt hat.
Anfang: “In der Nähe der Ausgabeschicht”
In frühen Deep-Learning-Modellen (z.B. einfachen mehrschichtigen Perzeptronen (MLP)) bezeichnete “Head” im Allgemeinen den letzten Teil des Netzwerks, der einen Merkmalsvektor als Eingabe erhält, der durch einen Merkmalsextraktor (Feature Extractor, Backbone) gegangen ist, um die endgültige Vorhersage (Klassifikation, Regression usw.) zu erstellen. In diesem Fall bestand der Head hauptsächlich aus vollständig verbundenen Schichten (fully connected layer) und Aktivierungsfunktionen (activation function).
Code
class SimpleModel(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.backbone = nn.Sequential( # Feature extractor
nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU()
)
self.head = nn.Linear(64, num_classes) # Head (output layer)
def forward(self, x):
features = self.backbone(x)
output = self.head(features)
return output- Mehrere Aufgaben lernen: “Aufgaben-spezifische Zweige”
Mit der Entwicklung von Deep-Learning-Modellen, die große Datensätze wie ImageNet verwenden, ist das Mehrfach-Aufgaben-Lernen (multi-task learning) aufgetaucht, bei dem mehrere Kopfmodelle von einem einzigen Feature-Extraktor abzweigen und verschiedene Aufgaben durchführen. Zum Beispiel werden in Objekterkennungsmodellen gleichzeitig ein Klassifikationskopf verwendet, um die Art der Objekte in einem Bild zu klassifizieren, und ein Regressionskopf, um die Position der Objekte durch Begrenzungsrahmen (bounding box) vorherzusagen.
Code
import torch
import torch.nn as nn
import torch.nn.functional as F
class MultiTaskModel(nn.Module):
def __init__(self, num_classes):
super().__init__()
self.backbone = ResNet50() # Feature extractor (ResNet)
self.classification_head = nn.Linear(2048, num_classes) # Classification head
self.bbox_head = nn.Linear(2048, 4) # Bounding box regression head
def forward(self, x):
features = self.backbone(x)
class_output = self.classification_head(features)
bbox_output = self.bbox_head(features)
return class_output, bbox_outputAttention is All You Need Paper (Transformer) “Head” Concept:
Der Multi-Head Attention des Transformers geht einen Schritt weiter. Im Transformer wird nicht mehr der fixe Begriff “Head = Teil, der den Ausgaben näher ist” beibehalten.
Code
class MultiHeadAttention(nn.Module):
def __init__(self, num_heads):
super().__init__()
self.heads = nn.ModuleList([
AttentionHead() for _ in range(num_heads) # num_heads개의 독립적인 어텐션 헤드
])- Unabhängige Module: Hier ist jeder “Head” ein eigenständiges Modul, das die Eingabe erhält und den Aufmerksamkeitsmechanismus unabhängig durchführt. Jeder Kopf hat unterschiedliche Gewichte und konzentriert sich auf verschiedene Aspekte der Eingabesequenz.
- Parallele Verarbeitung: Mehrere Köpfe arbeiten parallel, um verschiedene Arten von Informationen gleichzeitig zu verarbeiten.
- Zwischenschritte der Verarbeitung: Die Köpfe sind nicht mehr nur auf die Ausgabeebene beschränkt. Der Encoder und der Decoder des Transformers bestehen aus mehreren Schichten des Multi-Head-Aufmerksamkeitsmechanismus, wobei jeder Kopf in einer Schicht verschiedene Darstellungen (representations) der Eingabesequenz lernt.
Aktuelle Trends: “Funktionsmodule”
In jüngeren Deep-Learning-Modellen wird der Begriff “Head” flexibler verwendet. Oft werden unabhängige Module, die bestimmte Funktionen erfüllen, auch dann als “Heads” bezeichnet, wenn sie nicht in der Nähe der Ausgabeebene liegen.
- Sprachmodelle (Language Models): In großen Sprachmodellen wie BERT und GPT werden verschiedene Arten von Köpfen verwendet, wie “language modeling head”, “masked language modeling head” und “next sentence prediction head”.
- Bild-Transformatoren (Vision Transformers): Bei ViT wird das Bild in Patches unterteilt, und es gibt einen “patch embedding head”, der jeden Patch wie ein Token behandelt.
Fazit
In Deep Learning hat die Bedeutung von “Head” von einem “Teil, der nahe am Ausgang liegt” zu einem “unabhängigen Modul, das bestimmte Funktionen erfüllt (einschließlich paralleler und zwichschen Verarbeitungsschritte)” evolviert. Diese Entwicklung spiegelt die Tendenz wider, dass Teile des Modells in komplexeren und raffinierteren Deep-Learning-Architekturen zunehmend differenzierter und spezialisiert werden. Die Multi-Head-Aufmerksamkeit im Transformer ist ein hervorragendes Beispiel für diese Veränderung der Bedeutung, und der Begriff “Head” zeigt nicht mehr einen “Kopf”, sondern vielmehr eine Vielzahl von “Gehirnen”, die arbeiten.
8.3 Verarbeitung von Positionsinformationen
Herausforderung: Wie kann man ohne RNN die Ordnung der Wörter effektiv darstellen?
Forscherdilemma: Da Transformatoren Daten nicht sequentiell wie RNNs verarbeiten, mussten die Positionsinformationen der Wörter explizit bereitgestellt werden. Forscher probierten verschiedene Methoden (Positionsindizes, lernfähige Einbettungen usw.), aber sie erzielten keine zufriedenstellenden Ergebnisse. Es war wie das Entschlüsseln eines Chiffres; es musste eine neue Methode gefunden werden, um die Positionsinformationen effektiv darzustellen.
Transformatoren verwenden im Gegensatz zu RNNs weder rekurrente Strukturen noch Faltungsoperationen, daher mussten die Ordnungsinformationen der Sequenz separat bereitgestellt werden. “Hund beißt Mensch” und “Mensch beißt Hund” haben zwar die gleichen Wörter, aber sie bedeuten etwas völlig anderes je nach Reihenfolge. Die Aufmerksamkeitsoperation (\(QK^T\)) berechnet selbst nur die Ähnlichkeit zwischen Wortvektoren und berücksichtigt nicht die Positionsinformationen der Wörter; daher mussten die Forscherteams darüber nachdenken, wie sie diese Information in das Modell einbringen. Dies war die Herausforderung, wie man ohne RNN die Ordnung der Wörter effektiv darstellen kann.
8.3.1 Wichtigkeit von Sequenzinformationen
Die Forscherteams dachten über verschiedene Positionscodierungsmethoden nach.
- Direkte Verwendung von Positionsindizes: Der einfachste Ansatz besteht darin, die Positionsindizes (0, 1, 2, …) der einzelnen Wörter zu den Einbettungsvektoren hinzuzufügen.
Code
from dldna.chapter_08.visualize_positional_embedding import visualize_position_embedding
visualize_position_embedding()1. Original embedding matrix:
dim1 dim2 dim3 dim4
I [ 0.20][ 0.30][ 0.10][ 0.40]
love [ 0.50][ 0.20][ 0.80][ 0.10]
deep [ 0.30][ 0.70][ 0.20][ 0.50]
learning [ 0.60][ 0.40][ 0.30][ 0.20]
Each row is the embedding vector of a word
--------------------------------------------------
2. Position indices:
[0 1 2 3]
Indices representing the position of each word (starting from 0)
--------------------------------------------------
3. Embeddings with position information added:
dim1 dim2 dim3 dim4
I [ 0.20][ 0.30][ 0.10][ 0.40]
love [ 1.50][ 1.20][ 1.80][ 1.10]
deep [ 2.30][ 2.70][ 2.20][ 2.50]
learning [ 3.60][ 3.40][ 3.30][ 3.20]
Result of adding position indices to each embedding vector (broadcasting)
--------------------------------------------------
4. Changes due to adding position information:
I (0):
Original: [0.2 0.3 0.1 0.4]
Pos. Added: [0.2 0.3 0.1 0.4]
Difference: [0. 0. 0. 0.]
love (1):
Original: [0.5 0.2 0.8 0.1]
Pos. Added: [1.5 1.2 1.8 1.1]
Difference: [1. 1. 1. 1.]
deep (2):
Original: [0.3 0.7 0.2 0.5]
Pos. Added: [2.3 2.7 2.2 2.5]
Difference: [2. 2. 2. 2.]
learning (3):
Original: [0.6 0.4 0.3 0.2]
Pos. Added: [3.6 3.4 3.3 3.2]
Difference: [3. 3. 3. 3.]Aber dieser Ansatz hatte zwei Probleme.
- Nicht möglich, Sequenzen länger als die Trainingsdaten zu verarbeiten: Wenn eine Position (z.B. der 100. Ort), die während des Trainings nicht gesehen wurde, als Eingabe kommt, kann keine geeignete Darstellung gefunden werden.
- Schwierigkeit, relative Abstandsinformationen darzustellen: Es ist schwierig, auszudrücken, dass der Abstand zwischen Position 2 und 4 dem Abstand zwischen Position 102 und 104 entspricht.
- Lernfähige Positions-Embeddings: Es wurde auch überlegt, lernfähige Embedding-Vektoren für jede Position zu verwenden.
Code
# Conceptual code
positional_embeddings = nn.Embedding(max_seq_length, embedding_dim)
positions = torch.arange(seq_length)
positional_encoding = positional_embeddings(positions)
final_embedding = word_embedding + positional_encodingDiese Methode kann zwar positionsspezifische Darstellungen lernen, hat aber nach wie vor die grundlegende Beschränkung, dass sie Sequenzen verarbeiten kann, die länger sind als die Trainingsdaten.
Kernbedingungen für die Darstellung von Positionsinformationen
Die Forscherteams kamen durch diese Versuche und Irrtümer zu der Erkenntnis, dass die Darstellung von Positionsinformationen die folgenden drei Kernbedingungen erfüllen muss:
- Keine Sequenzlängenbegrenzung: Positionen (z.B. 1000. Position), die während des Trainings nicht gesehen wurden, müssen angemessen dargestellt werden können.
- Darstellung relativer Abstandsbeziehungen: Der Abstand zwischen den Positionen 2 und 4 muss gleich dem Abstand zwischen den Positionen 102 und 104 dargestellt werden. Das heißt, die relative Distanz zwischen den Positionen muss beibehalten werden.
- Kompatibilität mit Aufmerksamkeitsoperationen: Die Positionsinformationen dürfen die Berechnung der Aufmerksamkeitsgewichte nicht stören und müssen gleichzeitig die Reihenfolgeffekte effektiv vermitteln.
8.3.2 Design von Positional Encodings
Nach diesen Überlegungen fanden die Forscher eine einzigartige Lösung, den Positional Encoding, der sich auf die periodischen Eigenschaften von Sinus- und Kosinusfunktionen stützt.
Prinzip des sinus-kosinus-funktionsbasierten Positional Encodings
Wenn jede Position mit Sinus- und Kosinusfunktionen verschiedener Frequenzen kodiert wird, werden die relativen Abstände zwischen den Positionen natürlich dargestellt.
Code
from dldna.chapter_08.positional_encoding_utils import visualize_sinusoidal_features
visualize_sinusoidal_features()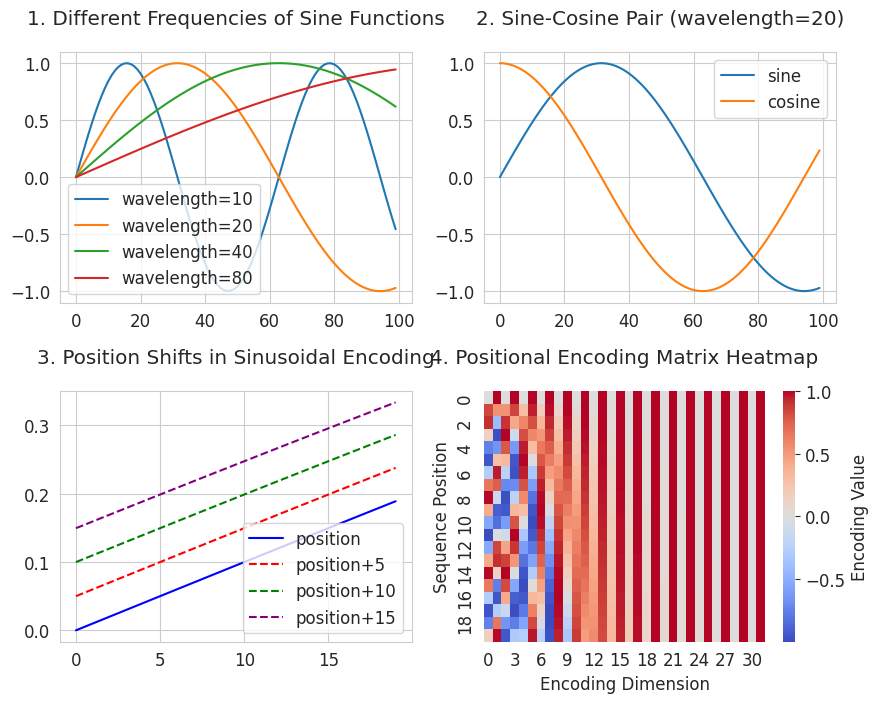
3 ist ein Diagramm, das die Verschiebung von Positionen visualisiert. Es zeigt, wie die Positionsbeziehungen durch eine Sinusfunktion dargestellt werden. Dies erfüllt die zweite Bedingung “Darstellung der relativen Distanzbeziehungen”. Alle verschobenen Kurven behalten dieselbe Form wie die ursprüngliche Kurve und haben einen konstanten Abstand zueinander. Dies bedeutet, dass die Beziehung gleich bleibt, wenn die Distanz zwischen den Positionen gleich ist (z.B. 2→7 und 102→107).
4 ist eine Heatmap der Positionsencodierung (Positional Encoding Matrix). Sie zeigt, welche einzigartigen Muster (X-Achse) zu verschiedenen Positionen (Y-Achse) gehören. Die Spalten auf der X-Achse stellen Sinus- und Kosinusfunktionen mit unterschiedlichen Perioden dar, wobei die Periode nach rechts hin länger wird. Jede Zeile (Position) hat ein einzigartiges Muster aus Rot (positiv) und Blau (negativ). Durch die Verwendung verschiedener Frequenzen von kurzer bis langer Periode werden für jede Position einzigartige Muster erstellt. Dieser Ansatz erfüllt die erste Bedingung “Keine Einschränkung der Sequenzlänge”. Durch Kombination von Sinus- und Kosinusfunktionen mit unterschiedlichen Perioden können mathematisch unendlich viele Positionen eindeutige Werte haben.
Mit diesen mathematischen Eigenschaften implementierten das Forschungsteam den Positionsencodierungsalgorithmus wie folgt.
Implementierung der Positionsencodierung
Code
def positional_encoding(seq_length, d_model):
# 1. 위치별 인코딩 행렬 생성
position = np.arange(seq_length)[:, np.newaxis] # [0, 1, 2, ..., seq_length-1]
# 2. 각 차원별 주기 계산
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
# 예: d_model=512일 때
# div_term[0] ≈ 1.0 (가장 짧은 주기)
# div_term[256] ≈ 0.0001 (가장 긴 주기)
# 3. 짝수/홀수 차원에 사인/코사인 적용
pe = np.zeros((seq_length, d_model))
pe[:, 0::2] = np.sin(position * div_term) # 짝수 차원
pe[:, 1::2] = np.cos(position * div_term) # 홀수 차원
return peposition: Array im Format[0, 1, 2, ..., seq_length-1]. Es stellt die Positionsindezes jedes Wortes dar.div_term: Wert, der die Periode für jede Dimension bestimmt. Die Periode wird größer, je größerd_modelist.pe[:, 0::2] = np.sin(position * div_term): Sinusfunktion wird auf gerade indizierte Dimensionen angewendet.pe[:, 1::2] = np.cos(position * div_term): Cosinusfunktion wird auf ungerade indizierte Dimensionen angewendet.
Mathematische Darstellung
Jede Dimension der Positionalcodierung wird nach folgender Formel berechnet:
- \(PE_{(pos, 2i)} = \sin(pos / 10000^{2i/d_{\text{model}}})\)
- \(PE_{(pos, 2i+1)} = \cos(pos / 10000^{2i/d_{\text{model}}})\)
Dabei
- \(pos\): Position des Wortes (0, 1, 2, …)
- \(i\): Dimensionsindex (0, 1, 2, …, \(d_{model}\)-1)
- \(d_{model}\): Einbettungsdimension (und Positions-Codierungsdimension)
Überprüfung der Periodenänderung
Code
from dldna.chapter_08.positional_encoding_utils import show_positional_periods
show_positional_periods()1. Periods of positional encoding:
First dimension (i=0): 1.00
Middle dimension (i=128): 100.00
Last dimension (i=255): 9646.62
2. Positional encoding formula values (10000^(2i/d_model)):
i= 0: 1.0000000000
i=128: 100.0000000000
i=255: 9646.6161991120
3. Actual div_term values (first/middle/last):
First (i=0): 1.0000000000
Middle (i=128): 0.0100000000
Last (i=255): 0.0001036633Hier ist der Schlüssel in drei Schritten.
Code
# 3. 짝수/홀수 차원에 사인/코사인 적용
pe = np.zeros((seq_length, d_model))
pe[:, 0::2] = np.sin(position * div_term) # 짝수 차원
pe[:, 1::2] = np.cos(position * div_term) # 홀수 차원Die obigen Ergebnisse zeigen die Änderung der Perioden in Abhängigkeit von der Dimension.
Finale Einbettung
Das generierte Positionscodierung pe hat die Form (seq_length, d_model) und wird zum ursprünglichen Worteinbettungsvektor (sentence_embedding) addiert, um die finale Einbettung zu erzeugen.
Code
final_embedding = sentence_embedding + positional_encodingSo wird die endgültige Einbettung sowohl mit der Bedeutung des Wortes als auch mit Positionsinformationen angereichert. Zum Beispiel kann das Wort “bank” je nach Position im Satz unterschiedliche Endvektoren haben, um so die Bedeutungen von “Bank” und “Ufer” zu unterscheiden.
Dadurch können Transformer sequentielle Informationen effektiv ohne RNN verarbeiten und die Vorteile paralleler Verarbeitung optimal nutzen.
Klicken Sie hier, um den Inhalt anzuzeigen (Tiefgang: Die Evolution der Positionscodierung, aktuelle Techniken und mathematische Grundlagen)
Die Evolution des Positional Encodings, aktuelle Techniken und mathematische Grundlagen
In Abschnitt 8.3.2 haben wir das sinus-cosinusfunktionen-basierte Positional Encoding betrachtet, das die Grundlage der Transformer-Modelle bildet. Seit der Veröffentlichung des Papers “Attention is All You Need” hat sich das Positional Encoding jedoch in verschiedenen Richtungen weiterentwickelt. In diesem Deep-Dive-Abschnitt behandeln wir lernfähige Positional Encodings, relative Positional Encodings und aktuelle Forschungstrends umfassend, wobei wir die mathematischen Darstellungen und Vor- und Nachteile jeder Technik im Detail analysieren.
1. Lernfähiges Positional Encoding (Learnable Positional Encoding)
Konzept: Anstatt feste Funktionen zu verwenden, lernt das Modell direkt die Embeddings, um Positionsinformationen darzustellen.
1.1 Mathematische Darstellung: Das lernfähige positionale Embedding wird durch folgende Matrix dargestellt.
\(P \in \mathbb{R}^{L_{max} \times d}\)
Hierbei ist \(L_{max}\) die maximale Sequenzlänge und \(d\) die Dimensionszahl des Embeddings. Das Embedding an Position \(i\) wird durch die \(i\)-te Zeile der Matrix \(P\), also \(P[i,:]\), gegeben.
1.2 Techniken zur Lösung des Extrapolationsproblems: Wenn Sequenzen verarbeitet werden müssen, die länger sind als die Lernsequenzen, besteht das Problem, dass es keine Informationen zu Positionen gibt, die außerhalb der gelernten Embeddings liegen. Es wurden Techniken entwickelt, um dieses Problem zu lösen.
Position Interpolation (Chen et al., 2023): Durch lineare Interpolation zwischen den gelernten Embeddings werden Embeddings für neue Positionen generiert. \(P_{ext}(i) = P[\lfloor \alpha i \rfloor] + (\alpha i - \lfloor \alpha i \rfloor)(P[\lfloor \alpha i \rfloor +1] - P[\lfloor \alpha i \rfloor])\)
Hierbei ist \(\alpha = \frac{\text{Sequenzlänge beim Lernen}}{\text{Sequenzlänge beim Inferenz}}\).
NTK-aware Skalierung (2023): Auf der Theorie des Neural Tangent Kernels (NTK) basierend, wird eine Methode verwendet, bei der die Frequenzen schrittweise erhöht werden, um einen Glättungseffekt einzuführen.
1.3 Aktuelle Anwendungsbeispiele:
- BERT: Ursprünglich auf 512 Tokens beschränkt, wurde es in RoBERTa auf 1024 Tokens erweitert.
- GPT-3: Es hat eine Obergrenze von 2048 Tokens und verwendet während des Trainings eine Methode, um die Sequenzlänge schrittweise zu erhöhen.
Vorteile:
- Flexibilität: Positionsinformationen, die auf die Daten abgestimmt sind, können gelernt werden.
- Erschwerungen bei der Verarbeitung langer Sequenzen: Zusätzliche Techniken zur Lösung des Extrapolationsproblems sind erforderlich.
2. Relatives Positional Encoding (Relative Positional Encoding)
Kernidee: Anstatt absolute Positionsinformationen, konzentriert man sich auf die relative Distanz zwischen den Wörtern.
Hintergrund: In natürlichen Sprachen wird die Bedeutung eines Wortes oft stärker von der relativen Beziehung zu umliegenden Wörtern als von seiner absoluten Position beeinflusst. Zudem haben absolute positionale Encodings den Nachteil, dass sie die Beziehungen zwischen weit entfernten Wörtern schlecht erfassen können.
2.1 Mathematische Erweiterung:
- Formel von Shaw et al. (2018): Bei der Berechnung der Beziehung zwischen Query- und Key-Vektoren im Attention-Mechanismus wird ein lernfähiges Embedding (\(a_{i-j}\)) hinzugefügt, das die relative Distanz berücksichtigt. \(e_{ij} = \frac{x_iW^Q(x_jW^K + a_{i-j})^T}{\sqrt{d}}\)
Hierbei ist \(a_{i-j} \in \mathbb{R}^d\) ein lernbarer Vektor für die relative Position \(i-j\).
Rotary Positional Encoding (RoPE): Verwendet Rotationsmatrizen, um relative Positionen zu kodieren.
\(\text{RoPE}(x, m) = x \odot e^{im\theta}\)
Hierbei ist \(\theta\) ein Hyperparameter, der die Frequenz steuert, und \(\odot\) steht für die komplexe Multiplikation (oder die entsprechende Rotationsmatrix).
Vereinfachte Version von T5: Verwendet einen lernbaren Bias \(b\) für relative Positionen und clippt den Wert, wenn der relative Abstand einen bestimmten Bereich überschreitet.
\(e_{ij} = \frac{x_iW^Q(x_jW^K)^T + b_{\text{clip}(i-j)}}{\sqrt{d}}\)
\(b \in \mathbb{R}^{2k+1}\) ist ein Biasvektor für die geklippten relativen Positionen [-k, k].
Vorteile:
- Verbesserte Generalisierungsfähigkeit: Bietet eine bessere Generalisierung für Sequenzenlängen, die nicht in den Trainingsdaten vorkommen.
- Verbesserter Fassung von langen Abhängigkeiten: Ermöglicht eine effektivere Modellierung von Beziehungen zwischen weit auseinander liegenden Wörtern.
Nachteile:
- Zunahme der Berechnungskomplexität: Da relative Abstände berücksichtigt werden müssen, kann die Aufmerksamkeitsberechnung komplexer werden. (Besonders wenn die relativen Abstände aller Wörterpaare berücksichtigt werden)
3. Optimierung von CNN-basierten Positional Encodings
3.1 Anwendung von Depth-wise Convolutions: Führt unabhängige Konvolutionen für jeden Kanal durch, um die Anzahl der Parameter zu reduzieren und die Berechnungseffizienz zu erhöhen. \(P(i) = \sum_{k=-K}^K w_k \cdot x_{i+k}\)
Hierbei ist \(K\) die Kernelgröße und \(w_k\) sind lernbare Gewichte.
3.2 Multi-Scale Convolutions: Nutzt parallele Konvolutionsschichten ähnlich wie in ResNet, um Positionsinformationen auf verschiedenen Skalen zu erfassen.
\(P(i) = \text{Concat}(\text{Conv}_{3x1}(x), \text{Conv}_{5x1}(x))\)
4. Dynamik rekursiver Positional Encodings
4.1 LSTM-basierte Encoding: Verwendet LSTMs, um sequenzielle Positionsinformationen zu kodieren.
\(h_t = \text{LSTM}(x_t, h_{t-1})\) \(P(t) = W_ph_t\)
4.2 Neueste Variation: Neural ODE: Modelliert die Dynamik durch eine Differentialgleichung und verwendet numerische Integratoren zur Berechnung der Positional Encoding.
\(\frac{dh(t)}{dt} = f_\theta(h(t), t)\) \(P(t) = \int_0^t f_\theta(h(\tau), \tau)d\tau\)
5. Quantenmechanische Interpretation komplexer Positional Encodings
5.1 Komplexe Embedding-Repräsentation: Kodiert Positionsinformationen in der Form von komplexen Zahlen.
\(z(i) = r(i)e^{i\phi(i)}\)
Hierbei ist \(r\) die Größe der Position und \(\phi\) der Phasenwinkel.
5.2 Theorem zur Phasenverschiebung: Drückt Positionsshifts als Rotationen in der komplexen Ebene aus.
\(z(i+j) = z(i) \cdot e^{i\omega j}\)
Hierbei ist \(\omega\) ein lernbarer Frequenzparameter.
6. Hybride Ansätze
6.1 Composite Positional Encoding: \(P(i)=αP_{abs}(i)+βP_{rel}(i)\)
\(P(i)=αP_{abs}(i)+βP_{rel}(i)\) α, β = lernbare Gewichte
6.2 Dynamische Positionierungskodierung:
\(P(i) = \text{MLP}(i, \text{Context})\) kontextabhängige Positionsrepräsentationen lernen
7. Experimentelle Leistungsvergleiche (GLUE Benchmark)
Die folgende Tabelle zeigt die experimentellen Leistungsvergleiche verschiedener Positionierungskodierungen im GLUE-Benchmark. (Die tatsächliche Leistung kann je nach Modellarchitektur, Daten und Hyperparameter-Einstellungen variieren.)
| Methode | Genauigkeit | Inferenzzeit (ms) | Speicherverbrauch (GB) |
|---|---|---|---|
| Absolut (Sinusoidal) | 88.2 | 12.3 | 2.1 |
| Relativ (RoPE) | 89.7 | 14.5 | 2.4 |
| CNN Multi-Scale | 87.9 | 13.8 | 3.2 |
| Komplex (CLEX) | 90.1 | 15.2 | 2.8 |
| Dynamische PE | 90.3 | 17.1 | 3.5 |
8. Aktuelle Forschungstrends (2024)
In der jüngsten Zeit werden neue Positionierungskodierungsverfahren erforscht, die von Quantencomputing und biologischen Systemen inspiriert sind.
- Quanten-Positionierungskodierung:
- Verwendung von Qubit-Rotationstoren: \(R_z(\theta_i)|x\rangle\)
- Positionssuche basierend auf dem Grover-Algorithmus
- Bio-inspirierte Kodierung:
- Anwendung der STDP (Spike-Timing-Dependent Plasticity)-Regel für Synapsenplastizität: \(\Delta w_{ij} \propto e^{-\frac{|i-j|}{\tau}}\)
- Integration von Graphennetzwerken:
- Darstellung von Positionen als Knoten und Beziehungen als Kanten: \(P(i) = \sum_{j \in \mathcal{N}(i)} \alpha_{ij}Wx_j\)
9. Auswahlleitfaden
- Feste Sequenzlänge: Lernbare PE. Geringes Überanpassungsrisiko und einfache Optimierung.
- Variable Länge/Extrapolation erforderlich: RoPE. Rotationsinvarianz bietet gute Skalierbarkeit in der Länge.
- Echtzeit-Verarbeitung mit niedriger Latenz: CNN-basiert. Optimierte parallele Verarbeitung, Hardwarebeschleunigung leicht möglich.
- Physische Signalverarbeitung: Komplexe PE. Frequenzinformationen erhalten. Kompatibilität mit Fourier-Transformation.
- Multimodale Daten: Dynamische PE. Anpassung an kross-modale Kontexte.
Mathematischer Anhang
Gruppentheoretische Eigenschaften von RoPE:
Darstellung der SO(2)-Rotationsgruppe: \(R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\)
Diese Eigenschaft garantiert die Erhaltung relativer Positionen in den Aufmerksamkeitspunkten.
Effizienter Berechnung von relativen Positionsverzerrungen:
Nutzung der Toeplitz-Matrix-Struktur: \(B = [b_{i-j}]_{i,j}\)
Implementierung mit FFT möglich, Komplexität \(O(n\log n)\)
Gradientenfluss komplexer PE:
Anwendung von Wirtinger-Differenzierungsregeln: \(\frac{\partial L}{\partial z} = \frac{1}{2}\left(\frac{\partial L}{\partial \text{Re}(z)} - i\frac{\partial L}{\partial \text{Im}(z)}\right)\)
Schlussfolgerung: Positionale Encoding ist ein entscheidender Faktor, der die Leistung von Transformer-Modellen erheblich beeinflusst und sich über einfache Sinus-Kosinus-Funktionen hinweg auf verschiedene Weisen entwickelt hat. Jede Methode verfügt über ihre eigenen Vor- und Nachteile sowie mathematische Grundlagen, wobei die Auswahl der geeigneten Methode abhängig von den Eigenschaften und Anforderungen des Problems ist. In jüngster Zeit werden neue positionale Encoding-Techniken erforscht, die aus verschiedenen Bereichen wie Quantencomputing und Biologie inspiriert sind, sodass eine kontinuierliche Weiterentwicklung erwartet wird.
8.4 Die gesamte Architektur des Transformers
Bislang haben wir uns mit der Entwicklung der Kernkomponenten des Transformers befasst. Nun werden wir uns damit beschäftigen, wie diese Elemente zu einer vollständigen Architektur integriert werden. Dies ist die gesamte Architektur des Transformers.
Quelle: The Illustrated Transformer (Jay Alammar, 2018) CC BY 4.0 Lizenz
Die für Bildungszwecke implementierte Quellcode des Transformers befindet sich in chapter_08/transformer. Diese Implementierung wurde angepasst unter Berücksichtigung von The Annotated Transformer der Harvard NLP Gruppe. Die wichtigsten Änderungen sind wie folgt:
- Modularisierung: Die Implementierung, die in einer Datei enthalten war, wurde in mehrere Module aufgeteilt, um Lesbarkeit und Wiederverwendbarkeit zu erhöhen.
- Adoption des Pre-LN-Strukturs: Im Gegensatz zum ursprünglichen Papier wurde eine Struktur verwendet, bei der die Layer-Normalisierung vor den Aufmerksamkeits-/Feedforward-Berechnungen angewendet wird (aktuelle Studien zeigen, dass Pre-LN für eine stabilere und bessere Leistung beim Lernen vorteilhaft ist).
- Hinzufügen der
TransformerConfig-Klasse: Eine separate Klasse zur Modellkonfiguration wurde eingeführt, um die Verwaltung von Hyperparametern zu erleichtern. - PyTorch-stilisierte Implementierung: PyTorch-Funktionen wie
nn.ModuleListwurden genutzt, um den Code kürzer und ansprechender zu gestalten. - Der Noam-Optimierer wurde implementiert, wird aber nicht verwendet.
8.4.1 Integration der grundlegenden Komponenten
Der Transformer besteht hauptsächlich aus Encoder und Decoder, wobei die einzelnen Komponenten wie folgt sind:
| Komponente | Encoder | Decoder |
|---|---|---|
| Multi-Head-Aufmerksamkeit | Selbst-Aufmerksamkeit (Self-Attention) | Maskierte Selbst-Aufmerksamkeit (Masked Self-Attention) |
| Encoder-Decoder-Aufmerksamkeit (Encoder-Decoder Attention) | ||
| Feedforward-Netzwerk | An jeder Position unabhängig angewendet | An jeder Position unabhängig angewendet |
| Residuerverbindungen | Eingang und Ausgang jeder Sub-Layer (Aufmerksamkeit, Feedforward) werden addiert | Eingang und Ausgang jeder Sub-Layer (Aufmerksamkeit, Feedforward) werden addiert |
| Layer-Normalisierung | Auf die Eingänge jedes Sub-Layers angewendet (Pre-LN) | Auf die Eingänge jedes Sub-Layers angewendet (Pre-LN) |
Encoder-Schicht - Code
Code
class TransformerEncoderLayer(nn.Module):
def __init__(self, config):
super().__init__()
self.attention = MultiHeadAttention(config)
self.feed_forward = FeedForward(config)
# SublayerConnection for Pre-LN structure
self.sublayer = nn.ModuleList([
SublayerConnection(config) for _ in range(2)
])
def forward(self, x, attention_mask=None):
x = self.sublayer[0](x, lambda x: self.attention(x, x, x, attention_mask))
x = self.sublayer[1](x, self.feed_forward)
return xMehrköpfige Aufmerksamkeit (Multi-Head Attention): Berechnet die Beziehungen zwischen allen Positionspaaren der Eingabe-Sequenz parallel. Jeder Kopf analysiert die Sequenz aus einer anderen Perspektive und die Ergebnisse werden zusammengefasst, um reichhaltige Kontextinformationen zu erfassen. (In dem Beispiel “The cat sits on the mat” lernen verschiedene Köpfe Beziehungen wie Subjekt-Verb, Präpositionalphrase, Artikel-Nomen usw.)
Feed-Forward Netzwerk: Ein Netzwerk, das unabhängig an jeder Position angewendet wird und aus zwei linearen Transformationen und einer GELU-Aktivierungsfunktion besteht.
Code
class FeedForward(nn.Module):
def __init__(self, config):
super().__init__()
self.linear1 = nn.Linear(config.hidden_size, config.intermediate_size)
self.linear2 = nn.Linear(config.intermediate_size, config.hidden_size)
self.activation = nn.GELU()
def forward(self, x):
x = self.linear1(x)
x = self.activation(x)
x = self.linear2(x)
return xDer Grund für die Notwendigkeit eines Feed-Forward-Netzwerks ist mit der Informationsdichte der Aufmerksamkeitsausgabe verbunden. Das Ergebnis des Aufmerksamkeitsverfahrens (\(\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d\_k}})V\)) ist eine gewichtete Summe der \(V\)-Vektoren, in denen Kontextinformationen konzentriert sind und die \(d\_{model}\) Dimension (im Papier 512) umfasst. Die direkte Anwendung der ReLU-Aktivierungsfunktion kann zu einem erheblichen Verlust dieser konzentrierten Informationen führen (ReLU setzt negative Werte auf 0). Daher erweitert das Feed-Forward-Netzwerk zunächst die \(d\_{model}\) Dimension auf eine größere Dimension (\(4 \times d\_{model}\), im Papier 2048), um den Ausdruckssaum zu vergrößern, wendet dann ReLU (oder GELU) an und reduziert ihn wieder auf die ursprüngliche Dimension, um Nichtlinearität hinzuzufügen.
Code
x = W1(x) # hidden_size -> intermediate_size (512 -> 2048)
x = ReLU(x) # or GELU
x = W2(x) # intermediate_size -> hidden_size (2048 -> 512)Residual Connection (Residuerverbindung): Es handelt sich um die Methode, die Eingabe und Ausgabe jeder Subschicht (Multi-Head Attention oder Feedforward-Netzwerk) zu addieren. Dies mildert das Problem der Verschwindenden/Explozierenden Gradienten und unterstützt das Training tiefer Netze. (Siehe Kapitel 7 über Residualverbindungen).
Layer Normalization (Schichtnormalisierung): Wird auf die Eingabe jeder Subschicht angewendet (Pre-LN).
Code
class LayerNorm(nn.Module):
def __init__(self, config):
super().__init__()
self.gamma = nn.Parameter(torch.ones(config.hidden_size))
self.beta = nn.Parameter(torch.zeros(config.hidden_size))
self.eps = config.layer_norm_eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = (x - mean).pow(2).mean(-1, keepdim=True).sqrt()
return self.gamma * (x - mean) / (std + self.eps) + self.betaSchichtnormierung (Layer Normalization) ist eine Technik, die 2016 in dem Paper “Layer Normalization” von Ba, Kiros und Hinton vorgeschlagen wurde. Während Batchnormierung (Batch Normalization) die Normierung entlang der Batch-Dimension durchführt, berechnet Schichtnormierung den Mittelwert und die Varianz für die Merkmalsdimension (feature dimension) jedes einzelnen Beispiels und normiert diese.
Vorteile der Schichtnormierung
- Unabhängig von der Batch-Größe: Da sie nicht von der Batch-Größe abhängt, funktioniert sie stabil auch bei kleineren Batches oder im Online-Lernen.
- Unabhängig von der Sequenzlänge: Sie ist geeignet für Modelle wie RNNs und Transformers, die sequenzielle Daten mit variabler Länge verarbeiten.
- Stabilisierung und Beschleunigung des Lernens: Durch Stabilisierung der Eingabeverteilung jeder Schicht werden Gradientenverschwinden/-explosionen gemildert und das Lern Tempo wird erhöht.
In Transformers wird die Pre-LN-Methode verwendet, bei der die Schichtnormierung vor dem Durchgang durch jede Subschicht (Multi-Head-Aufmerksamkeit, Feedforward-Netzwerk) angewendet wird.
Visualisierung der Schichtnormierung
Code
from dldna.chapter_08.visualize_layer_norm import visualize_layer_normalization
visualize_layer_normalization()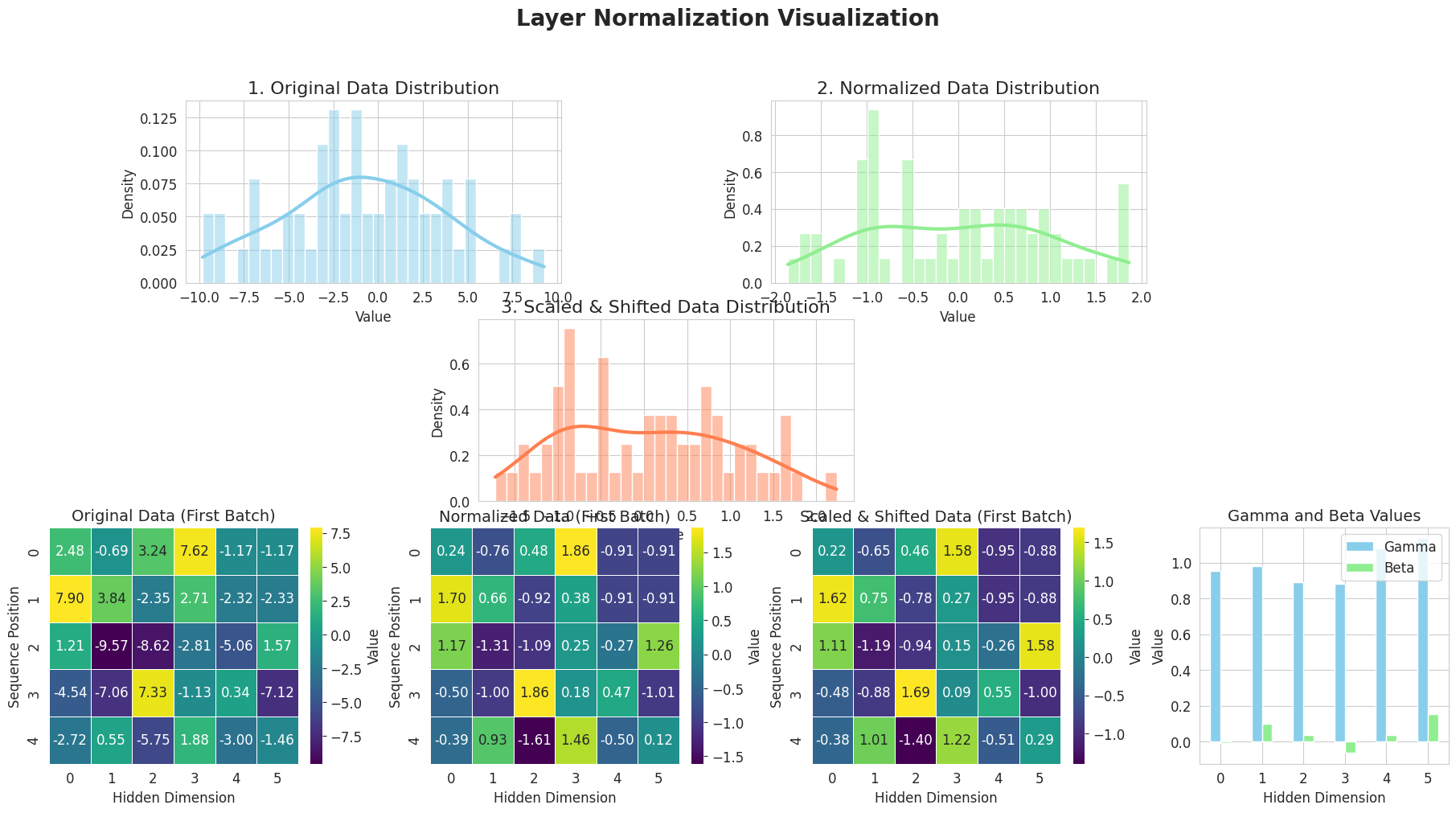
========================================
Input Data Shape: (2, 5, 6)
Mean Shape: (2, 5, 1)
Standard Deviation Shape: (2, 5, 1)
Normalized Data Shape: (2, 5, 6)
Gamma (Scale) Values:
[0.95208258 0.9814341 0.8893665 0.88037934 1.08125258 1.135624 ]
Beta (Shift) Values:
[-0.00720101 0.10035329 0.0361636 -0.06451198 0.03613956 0.15380366]
Scaled & Shifted Data Shape: (2, 5, 6)
========================================Das obige Diagramm zeigt schrittweise den Ablauf der Layer-Normalisierung (Layer Normalization).
- Urdaten (oben links): Die Daten vor der Normalisierung sind weit verstreut und haben einen ungleichmäßigen Mittelwert und Standardabweichung.
- Nach Normalisierung (oben rechts): Die Daten werden so normalisiert, dass sie sich um den Mittelwert 0 und die Standardabweichung 1 sammeln.
- Skalierung und Verschiebung (Mitte): Durch Anwendung lernbarer Parameter γ (Gamma, Skalierung) und β (Beta, Verschiebung) wird der Datenverteilung eine leichte Veränderung hinzugefügt. Dies regelt die Ausdrucksfähigkeit des Modells.
- Heatmap (unten): Basierend auf den ersten Batch-Daten zeigt dies die individuellen Wertänderungen vor und nach Normalisierung sowie nach Anwendung von Skalierung/Verschiebung.
- γ/β Werte (unten rechts): Die γ- und β-Werte für jede verborgene Dimension werden in einem Balkendiagramm dargestellt.
Auf diese Weise verbessert die Layer-Normalisierung durch Normalisierung der Eingaben jeder Schicht die Lernstabilität und -geschwindigkeit.
Kernpunkte:
- Normalisierung der Eingaben jeder Schicht (Mittelwert 0, Standardabweichung 1)
- Regulierung der Ausdrucksfähigkeit durch lernbare Skalierung (γ) und Verschiebung (β)
- Im Gegensatz zur Batch-Normalisierung wird die Unabhängigkeit zwischen Stichproben beibehalten
Diese Komponenten (Multikopf-Aufmerksamkeit, Feedforward-Netzwerk, Residualverbindungen, Layer-Normalisierung) in Kombination maximieren die Vorteile jeder Komponente. Die Multikopf-Aufmerksamkeit fängt verschiedene Aspekte der Eingabe-Sequenz ein, das Feedforward-Netzwerk fügt Nichtlinearität hinzu, und Residualverbindungen sowie Layer-Normalisierung ermöglichen stabiles Lernen auch in tiefen Netzen.
8.4.2 Architektur des Encoders
Der Transformer verfügt über eine Encoder-Decoder-Architektur für maschinelle Übersetzung. Der Encoder analysiert die Quellsprache (z.B. Englisch), während der Decoder das Zielsprache (z.B. Französisch) generiert. Obwohl beide, Encoder und Decoder, Multikopf-Attention und Feedforward-Netze als grundlegende Bestandteile teilen, sind sie je nach spezifischem Anwendungsfall unterschiedlich aufgebaut.
Vergleich von Encoder und Decoder-Aufbau
| Komponente | Encoder | Decoder |
|---|---|---|
| Anzahl der Attention-Schichten | 1 (Selbst-Attention) | 2 (Maskierte Selbst-Attention, Encoder-Decoder-Attention) |
| Maskierungsstrategie | Nur Padding-Maske | Padding-Maske + Causal-Maske |
| Kontextverarbeitung | Bidirektionale Kontextverarbeitung | Unidirektionale Kontextverarbeitung (rekursiv) |
| Eingabe-Referenz | Bezieht sich nur auf eigene Eingaben | Eigene Eingaben + Ausgabe des Encoders |
Wir fassen verschiedene Attention-Begriffe wie folgt zusammen:
Zusammenfassung der Attention-Konzepte
| Art der Attention | Merkmale | Erklärungsstandort | Kernkonzepte |
|---|---|---|---|
| Attention (grundlegend) | - Ähnlichkeitsberechnung durch gleiche Wortvektoren - Einfache Gewichtete Summe zur Kontextinformationserstellung - Vereinfachte Version der Anwendung in seq2seq-Modellen |
8.2.2 | - Berechnung der Ähnlichkeit durch das Skalarprodukt von Wortvektoren - Umwandlung der Gewichte mit softmax - Padding-Maske wird standardmäßig auf alle Attention-Arten angewendet |
| Selbst-Attention (Self-Attention) | - Trennung in Q, K, V-Räume - Unabhängige Optimierung jedes Raumes - Die Eingabesequenz referenziert sich selbst - Verwendet im Encoder |
8.2.3 | - Getrennte Rollen für die Berechnung der Ähnlichkeit und Informationsübertragung - Lernfähige Q, K, V-Transformationen - Bidirektionale Kontextverarbeitung möglich |
| Maskierte Selbst-Attention | - Verhindert Zukunftsinformation - Causal-Maske wird verwendet - Verwendet im Decoder |
8.2.5 | - Maskierung zukünftiger Informationen durch obere Dreiecksmatrix - Rekursive Generierung möglich - Unidirektionale Kontextverarbeitung |
| Kreuz- (Encoder-Decoder-) Attention | - Query: Decoder-Zustand - Key, Value: Encoder-Ausgabe - Wird auch als Cross-Attention bezeichnet - Verwendet im Decoder |
8.4.3 | - Der Decoder referenziert die Encoder-Informationen - Berechnung der Beziehungen zwischen zwei Sequenzen - Kontextberücksichtigung bei Übersetzung/Generierung |
Im Transformer werden die Begriffe Selbst-, maskierte und Kreuz-Attention verwendet. Das Attention-Mechanismus ist identisch, wobei sich die Unterschiede auf den Ursprung von Q, K, V beziehen.
Encoder-Komponenten | Komponente | Beschreibung | | —————————– | ————————————————————————————- | | Embeddings | Wandelt Eingabetoken in Vektoren um und fügt Positionsinformationen hinzu, um die Bedeutung und Reihenfolge der Eingabesequenz zu kodieren. | | TransformerEncoderLayer (x N) | Stapelt identische Layer in mehreren Schichten, um aus der Eingabesequenz auf steigender Ebene abstraktere und komplexere Merkmale zu extrahieren. | | LayerNorm | Normalisiert die Verteilung der Merkmale des finalen Outputs, um sie zu stabilisieren und für den Decoder in eine nützliche Form zu bringen. |
Code
class TransformerEncoder(nn.Module):
def __init__(self, config):
super().__init__()
self.embeddings = Embeddings(config)
self.layers = nn.ModuleList([
TransformerEncoderLayer(config)
for _ in range(config.num_hidden_layers)
])
self.norm = LayerNorm(config)
def forward(self, input_ids, attention_mask=None):
x = self.embeddings(input_ids)
for i, layer in enumerate(self.layers):
x = layer(x, attention_mask)
output = self.norm(x)
return outputDer Encoder besteht aus einem Embedding-Layer, mehreren Encoder-Layern und einer finalen Normalisierungsschicht.
1. Selbst-Aufmerksamkeits-Mechanismus (Beispiel)
Die Selbst-Aufmerksamkeit des Encoders berechnet die Beziehungen zwischen allen Wörternpaaren in der Eingangsequenz, um den Kontext jeder einzelnen Wort reichhaltiger zu gestalten.
- Beispiel: “The patient bear can bear the pain no longer.”
- Rolle: Bei der Bestimmung der Bedeutung des zweiten ‘bear’, berücksichtigt die Selbst-Aufmerksamkeit die Beziehungen aller Wörter im Satz, einschließlich ‘patient’ (Kranker), ‘bear’ (Bär) und ‘pain’ (Schmerz). So kann es präzise erkannt werden, dass ‘bear’ hier als ‘aushalten’, ‘ertragen’ verwendet wird (verarbeitung des bidirektionalen Kontexts).
2. Die Bedeutung der Position von Dropout
Dropout spielt eine wichtige Rolle bei der Verhinderung von Überanpassung und dem Erhöhen der Lernstabilität. Im Transformer-Encoder wird Dropout an folgenden Stellen angewendet:
- Nach Embedding-Ausgabe: Unmittelbar nachdem die Token-Embeddings und die Positionsinformationen kombiniert wurden.
- Nach Ausgabe jeder Subschicht (Attention, FFN): Es wird eine Pre-LN Struktur (Normalisierung → Subschicht → Dropout → Residualverbindung) verwendet.
- Innerhalb der FFN: Nach der ersten linearen Transformation und Anwendung der ReLU-Aktivierungsfunktion.
Diese Dropout-Plazierung reguliert den Informationsfluss, um zu verhindern, dass das Modell übermäßig von bestimmten Merkmalen abhängt und die Generalisierungsleistung zu verbessern.
3. Struktur des Encoder-Stacks
Der Transformer-Encoder besteht aus einer Stapelstruktur (stacked) identischer Encoder-Schichten.
- Ursprüngliche Publikation: Verwendung von 6 Encoder-Layern.
- Rollenverteilung:
- Untere Layer: Lernen von oberflächlichen Sprachmuster, wie benachbarte Wörter und Satzzeichen.
- Mittlere Layer: Lernen von grammatikalischen Strukturen.
- Obere Layer: Lernen komplexer semantischer Beziehungen, wie coreference.
Je tiefer die Schichten gestapelt sind, desto abstraktere und komplexere Merkmale können gelernt werden. Spätere Studien ermöglichten es dank technologischem Fortschritt (Pre-LayerNorm, Gradient Clipping, Lernrate Warming-Up, Mixed-Precision Training, Gradient Accumulation usw.), Modelle mit weit mehr Schichten zu bauen (BERT-base: 12 Layer, GPT-3: 96 Layer, PaLM: 118 Layer).
4. Die Endausgabe des Encoders und die Nutzung durch den Decoder
Die endgültige Ausgabe des Encoders ist eine Vektordarstellung, die reichhaltige kontextuelle Informationen für jedes Eingabetoken enthält. Diese Ausgabe wird im Encoder-Decoder-Aufmerksamkeit (Cross-Attention) als Key und Value verwendet. Der Decoder bezieht sich bei der Generierung jeder Tokendes Ausgabesequenz auf die Encoderausgabe, um eine genaue Übersetzung/Ergänzung unter Berücksichtigung des Kontexts des Originalsatzes durchzuführen.
8.4.3 Struktur des Decoders
Der Decoder ist dem Encoder类似，但不同之处在于它以自回归（autoregressive）的方式生成输出。
Gesamter Code für die Decoder-Schicht
Code
class TransformerDecoderLayer(nn.Module):
def __init__(self, config):
super().__init__()
self.self_attn = MultiHeadAttention(config)
self.cross_attn = MultiHeadAttention(config)
self.feed_forward = FeedForward(config)
# Pre-LN을 위한 레이어 정규화
self.norm1 = LayerNorm(config)
self.norm2 = LayerNorm(config)
self.norm3 = LayerNorm(config)
self.dropout = nn.Dropout(config.dropout_prob)
def forward(self, x, memory, src_mask=None, tgt_mask=None):
# Pre-LN 구조
m = self.norm1(x)
x = x + self.dropout(self.self_attn(m, m, m, tgt_mask))
m = self.norm2(x)
x = x + self.dropout(self.cross_attn(m, memory, memory, src_mask))
m = self.norm3(x)
x = x + self.dropout(self.feed_forward(m))
return x| Subschicht | Rolle | Implementierungseigenschaften |
|---|---|---|
| Maskierte Selbst-Aufmerksamkeit | Beziehungen zwischen Wörtern in der bisher erzeugten Ausgabesequenz erkennen, Vermeidung des Zugriffs auf zukünftige Informationen (autoregressives Erzeugen) | Verwendung von tgt_mask (Kausalitätsmaske + Padding-Maske), self.self_attn |
| Enkoder-Dekoder-Aufmerksamkeit (Cross-Attention) | Der Dekoder bezieht sich auf die Ausgabe des Enkoders (Kontextinformationen des Eingabetexts), um Informationen zu dem derzeit zu erzeugenden Wort zu erhalten | Q: Dekoder, K, V: Enkoder, Verwendung von src_mask (Padding-Maske), self.cross_attn |
| Feed-Forward-Netzwerk | Unabhängige Transformation der Repräsentationen an jeder Position zur Erstellung reichhaltigerer Repräsentationen | Identische Struktur wie beim Enkoder, self.feed_forward |
| Layer-Normalisierung (LayerNorm) | Normalisierung der Eingänge jedes Sublayers (Pre-LN), Verbesserung von Lernstabilität und -leistung | self.norm1, self.norm2, self.norm3 |
| Dropout | Vermeidung des Überanpassens, Steigerung der Generalisierungsfähigkeit | Anwendung auf die Ausgänge jedes Sublayers, self.dropout |
| Residualverbindung (Residual Connection) | Linderung von Gradienten-Verschwinden/-Explosion-Problemen in tiefen Netzen, Verbesserung des Informationsflusses | Addieren der Eingänge und Ausgänge jedes Sublayers |
1. Maskierte Selbst-Aufmerksamkeit (Masked Self-Attention) * Rolle: Der Decoder generiert die Ausgabe autoregressiv. Das heißt, er kann auf zukünftige Wörter, die noch nicht erstellt wurden, nicht zugreifen. Zum Beispiel, beim Übersetzen von “I love you”, kann nach der Generierung von “Ich” das System bei der Generierung von “dich” den noch nicht generierten Token “liebe” nicht berücksichtigen. * Implementierung: Eine Kombination aus dem Causal Mask und Padding Mask, genannt tgt_mask, wird verwendet. Die Causal Mask füllt die obere Dreiecksmatrix mit -inf um die Aufmerksamkeitsgewichte für zukünftige Token auf 0 zu setzen (siehe Abschnitt 8.2.5). In der forward Methode von TransformerDecoderLayer wird diese Maske in dem Teil self.self_attn(m, m, m, tgt_mask) angewendet.
2. Encoder-Decoder Attention (Cross-Attention)
- Rolle: Der Decoder verwendet die Ausgabe des Encoders (den Kontext der Eingabezeichenfolge) um Informationen zu dem aktuellen zu generierenden Wort zu erhalten. Dies ist entscheidend bei Übersetzungsprozessen, da es den Decoder ermöglicht, die Bedeutung der ursprünglichen Zeichenfolge genau zu verstehen und geeignete Übersetzungswörter auszuwählen.
- Implementierung:
- Query (Q): Der aktuelle Zustand des Decoders (Ausgabe der maskierten Selbst-Aufmerksamkeit)
- Key (K): Die Ausgabe des Encoders (
memory) - Value (V): Die Ausgabe des Encoders (
memory) src_mask(Padding Mask) wird verwendet, um Padding-Token in der Encoder-Ausgabe zu ignorieren.- In der
forwardMethode vonTransformerDecoderLayerwird die Aufmerksamkeit im Teilself.cross_attn(m, memory, memory, src_mask)durchgeführt.memoryrepräsentiert die Ausgabe des Encoders.
3. Decoder-Stack-Architektur
Code
class TransformerDecoder(nn.Module):
def __init__(self, config):
super().__init__()
self.embeddings = Embeddings(config)
self.layers = nn.ModuleList([
TransformerDecoderLayer(config)
for _ in range(config.num_hidden_layers)
])
self.norm = LayerNorm(config)
def forward(self, x, memory, src_mask=None, tgt_mask=None):
x = self.embeddings(x)
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)- Der Decoder besteht aus mehreren Schichten von
TransformerDecoderLayer(im ursprünglichen Papier waren es 6). - Jede Schicht führt sequentiell masked self-attention, encoder-decoder attention und feedforward network durch.
- Pre-LN Struktur und residuelle Verbindungen werden in jeder Subschicht angewendet. Dies ermöglicht stabiles Training auch bei tiefen Netzwerken.
- Die
forwardMethode der KlasseTransformerDecodernimmt die Eingabex(Decoder-Eingabe),memory(Encoder-Ausgabe),src_mask(Encoder-Padding-Maske) undtgt_mask(Decoder-Maske) entgegen, führt sie sequentiell durch die Decoder-Schichten und gibt die finale Ausgabe zurück.
Modellspezifische Anzahl der Encoder/Decoder-Schichten
| Modell | Jahr | Struktur | Encoder-Schichten | Decoder-Schichten | Gesamt-Parameter |
|---|---|---|---|---|---|
| Originaltransformer | 2017 | Encoder-Decoder | 6 | 6 | 65M |
| BERT-base | 2018 | Nur-Encoder | 12 | - | 110M |
| GPT-2 | 2019 | Nur-Decoder | - | 48 | 1.5B |
| T5-base | 2020 | Encoder-Decoder | 12 | 12 | 220M |
| GPT-3 | 2020 | Nur-Decoder | - | 96 | 175B |
| PaLM | 2022 | Nur-Decoder | - | 118 | 540B |
| Gemma-2 | 2024 | Nur-Decoder | - | 18-36 | 2B-27B |
Neuere Modelle können dank fortgeschrittener Trainierungstechniken wie Pre-LN effektiver mehr Schichten lernen. Ein tieferer Decoder kann abstraktere und komplexere Sprachmuster lernen, was zu Leistungsverbesserungen in verschiedenen NLP-Aufgaben wie Übersetzung und Textgenerierung führt.
4. Generierung des Decoder-Ausgangs und Beendigungsbedingung
- Ausgabeerzeugung: Die
generatorMethode (lineare Schicht) der KlasseTransformerkonvertiert die finale Ausgabe des Decoders in einen Logit-Vektor der Größe des Vokabulars (vocab_size) und wendetlog_softmaxan, um die Wahrscheinlichkeitsverteilung für jedes Token zu erhalten. Basierend auf dieser Wahrscheinlichkeitsverteilung wird das nächste Token vorhergesagt.
Code
# 최종 출력 생성 (설명용)
output = self.generator(decoder_output)
return F.log_softmax(output, dim=-1)- Beendigungsbedingungen
- Maximale Länge erreicht: Wenn die vordefinierte maximale Ausgabelänge erreicht ist.
- Benutzerdefinierte Beendigungsbedingung: Wenn bestimmte Bedingungen (z.B. Satzzeichen) erfüllt sind.
- Spezielle Token generiert: Wenn spezielle Tokens, die das Ende eines Satzes anzeigen (
<eos>,</s>usw.), generiert werden. Der Decoder lernt während des Trainingsprozesses, diese speziellen Tokens am Ende eines Satzes hinzuzufügen.
- Token-Generierungsstrategien
Es gibt Token-Generierungsstrategien, die normalerweise nicht Teil des Decoders sind, aber das Ergebnis der Ausgabe beeinflussen.
| Generierungsstrategie | Funktionsweise | Vorteile | Nachteile | Beispiel |
|---|---|---|---|---|
| Greedy Search | Bei jedem Schritt wird das Token mit der höchsten Wahrscheinlichkeit ausgewählt. | Schnell, einfache Implementierung | Möglichkeit lokaler Optima, Mangel an Vielfalt | “Ich” gefolgt von → “gehe zur Schule” (höchste Wahrscheinlichkeit) |
| Beam Search | k Pfade werden gleichzeitig verfolgt. |
Umfassende Suche, bessere Ergebnisse möglich | Hoher Rechenaufwand, begrenzte Vielfalt | k=2: “Ich gehe zur Schule”, “Ich gehe nach Hause” beibehalten und nächsten Schritt fortsetzen |
| Top-k Sampling | Auswahl von den oberen k Wahrscheinlichkeiten proportional zu ihrer Wahrscheinlichkeit. |
Angemessene Vielfalt, Vermeidung seltsamer Tokens | Schwierige Einstellung des k-Werts, kontextabhängige Leistung |
k=3: “Ich” gefolgt von → {“gehe zur Schule”, “gehe nach Hause”, “gehe in den Park”} aus denen proportional zur Wahrscheinlichkeit gewählt wird |
| Nucleus Sampling | Auswahl der Token, deren kumulative Wahrscheinlichkeit p erreicht. |
Dynamische Kandidatenmenge, flexibel im Kontext | Einstellung des p-Werts erforderlich, erhöhter Rechenaufwand |
p=0.9: “Ich” gefolgt von → {“gehe zur Schule”, “gehe nach Hause”, “gehe in den Park”, “esse”} aus denen die kumulative Wahrscheinlichkeit 0.9 nicht überschreiten |
| Temperature Sampling | Anpassung der Wahrscheinlichkeitsverteilung (niedrig = sicher, hoch = vielfältig). | Regulierung der Ausgabe-Kreativität, einfache Implementierung | Zu hoch: unangemessen, zu niedrig: wiederholter Text | T=0.5: Betonung hoher Wahrscheinlichkeiten, T=1.5: Erhöhung der Möglichkeit niedriger Wahrscheinlichkeiten auszuwählen |
Diese Token-Generierungsstrategien werden in der Regel als separate Klassen oder Funktionen implementiert, die unabhängig vom Decoder stehen.
8.4.4 Erklärung der gesamten Struktur
Bislang haben wir die Designabsichten und den Funktionsmechanismus des Transformers verstanden. Auf Grundlage der bisherigen Erläuterungen bis 8.4.3 werden wir uns nun die gesamte Struktur des Transformers ansehen. Die Implementierung wurde unter Berücksichtigung von Havard NLP modularisiert und strukturell angepasst, wobei ich sie so prägnant wie möglich für Lernzwecke erstellt habe. In einem echten Produktionsumfeld sind zusätzliche Anforderungen zu berücksichtigen, wie Typen Hinweise zur Codestabilität, effiziente Verarbeitung von mehrdimensionalen Tensoren, Eingabevalidierung und Fehlertests, Speicheroptimierungen sowie Erweiterbarkeit für die Unterstützung verschiedener Konfigurationen.
Der Code befindet sich im Verzeichnis chapter_08/transformer.
Rolle und Implementierung der Embedding-Schicht
Der erste Schritt des Transformers ist die Embedding-Schicht, die Eingabetoken in den Vektorraum transformiert. Die Eingabe besteht aus einer Sequenz ganzzahliger Token-IDs (z.B. [101, 2045, 3012, …]), wobei jede Token-ID einen eindeutigen Index im Wörterbuch darstellt. Die Embedding-Schicht mappt diese IDs auf hochdimensionale Vektoren (Embedding-Vektoren).
Die Dimension der Embedding-Ebene hat einen großen Einfluss auf die Leistung des Modells. Eine große Dimension ermöglicht es, reichhaltige semantische Informationen darzustellen, steigert jedoch auch den Berechnungsaufwand. Eine kleine Dimension wirkt sich umgekehrt aus.
Nach Durchlaufen der Embedding-Schicht ändern sich die Tensor-Dimensionen wie folgt:
- Eingabe: (batch_size, seq_length) → Ausgabe: (batch_size, seq_length, hidden_size)
- Beispiel: (32, 50) → (32, 50, 768)
Im Folgenden finden Sie ein Codebeispiel zur Durchführung von Embedding im Transformer.
Code
import torch
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.embeddings import Embeddings
# Create a configuration object
config = TransformerConfig()
config.vocab_size = 1000 # Vocabulary size
config.hidden_size = 768 # Embedding dimension
config.max_position_embeddings = 512 # Maximum sequence length
# Create an embedding layer
embedding_layer = Embeddings(config)
# Generate random input tokens
batch_size = 2
seq_length = 4
input_ids = torch.tensor([
[1, 5, 9, 2], # First sequence
[6, 3, 7, 4] # Second sequence
])
# Perform embedding
embedded = embedding_layer(input_ids)
print(f"Input shape: {input_ids.shape}")
# Output: Input shape: torch.Size([2, 4])
print(f"Shape after embedding: {embedded.shape}")
# Output: Shape after embedding: torch.Size([2, 4, 768])
print("\nPart of the embedding vector for the first token of the first sequence:")
print(embedded[0, 0, :10]) # Print only the first 10 dimensionsInput shape: torch.Size([2, 4])
Shape after embedding: torch.Size([2, 4, 768])
Part of the embedding vector for the first token of the first sequence:
tensor([-0.7838, -0.9194, 0.4240, -0.8408, -0.0876, 2.0239, 1.3892, -0.4484,
-0.6902, 1.1443], grad_fn=<SliceBackward0>)Konfigurationsklasse
TransformerConfig-Klasse definiert alle Hyperparameter des Modells.
Code
class TransformerConfig:
def __init__(self):
self.vocab_size = 30000 # Vocabulary size
self.hidden_size = 768 # Hidden layer dimension
self.num_hidden_layers = 12 # Number of encoder/decoder layers
self.num_attention_heads = 12 # Number of attention heads
self.intermediate_size = 3072 # FFN intermediate layer dimension
self.hidden_dropout_prob = 0.1 # Hidden layer dropout probability
self.attention_probs_dropout_prob = 0.1 # Attention dropout probability
self.max_position_embeddings = 512 # Maximum sequence length
self.layer_norm_eps = 1e-12 # Layer normalization epsilonvocab_size ist die Gesamtzahl der einzigartigen Tokens, die das Modell verarbeiten kann. Hier wurde es auf 30.000 gesetzt, unter der Annahme einer einfachen Implementierung mit Wort-Weise-Tokenisierung. In realen Sprachmodellen werden verschiedene Sub-Wort-Tokenisierer wie BPE (Byte Pair Encoding), Unigram und WordPiece verwendet, wodurch vocab_size kleiner sein kann. Zum Beispiel kann das Wort ‘playing’ in ‘play’ und ‘ing’ aufgeteilt werden, so dass es nur mit zwei Sub-Wörtern dargestellt wird.
Änderung der Tensor-Dimensionen bei Attention
Bei Multi-Head-Attention werden die Dimensionen des Eingabetensors umgeordnet, damit jeder Kopf unabhängig die Aufmerksamkeit berechnen kann.
Code
class MultiHeadAttention(nn.Module):
def forward(self, query, key, value, mask=None):
batch_size = query.size(0)
# Linear transformations and head splitting
query = self.linears[0](query).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
key = self.linears[1](key).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
value = self.linears[2](value).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)Die Dimensionswandlung erfolgt wie folgt:
- Eingabe: (batch_size, seq_len, d_model)
- Lineare Transformation: (batch_size, seq_len, d_model)
view: (batch_size, seq_len, h, d_k)transpose: (batch_size, h, seq_len, d_k)
Hierbei ist h die Anzahl der Köpfe und d_k die Dimension jedes Kopfes (d_model / h). Durch diese Neuanordnung der Dimensionen berechnet jeder Kopf unabhängig die Aufmerksamkeit.
Die zusammengefügte Struktur des Transformers
Schließlich betrachten wir die Transformer-Klasse, die alle Komponenten vereint.
Code
class Transformer(nn.Module):
def __init__(self, config: TransformerConfig):
super().__init__()
self.encoder = TransformerEncoder(config)
self.decoder = TransformerDecoder(config)
self.generator = nn.Linear(config.hidden_size, config.vocab_size)
self._init_weights()Der Transformer besteht aus drei Hauptkomponenten.
- Encoder: Verarbeitet die Eingabesequenz.
- Decoder: Erzeugt die Ausgabesequenz.
- Generator: Wandelt den Decoder-Ausgang in Vokabelwahrscheinlichkeiten um.
Die forward-Methode verarbeitet die Daten in der folgenden Reihenfolge.
Code
def forward(self, src, tgt, src_mask=None, tgt_mask=None):
# Encoder-decoder processing
encoder_output = self.encode(src, src_mask)
decoder_output = self.decode(encoder_output, src_mask, tgt, tgt_mask)
# Generate final output
output = self.generator(decoder_output)
return F.log_softmax(output, dim=-1)Die Änderung der Tensor-Dimensionen ist wie folgt:
- Eingabe (
src,tgt): (batch_size, seq_len) - Encoder-Ausgabe: (batch_size, src_len, hidden_size)
- Decoder-Ausgabe: (batch_size, tgt_len, hidden_size)
- Endausgabe: (batch_size, tgt_len, vocab_size)
Im nächsten Abschnitt werden wir diese Struktur an einem praktischen Beispiel anwenden.
8.5 Transformer-Beispiele
Bislang haben wir die Struktur und das Funktionsprinzip von Transformatoren untersucht. Nun werden wir durch praktische Beispiele das Verhalten der Transformer prüfen. Die Beispiele sind nach Schwierigkeitsgrad geordnet, wobei jedes Beispiel dazu dient, bestimmte Funktionen des Transformers zu verstehen. Die Beispiele zeigen Schritt für Schritt, wie man verschiedene Datenverarbeitungs- und Modellgestaltungsaufgaben in realen Projekten löst. Insbesondere werden Themen behandelt, die im Praktischen erforderlich sind, wie Datenpräprozessierung, Design von Verlustfunktionen und Festlegung von Bewertungskriterien. Die Beispiele befinden sich unter transformer/examples.
examples
├── addition_task.py # 8.5.2 Additionsaufgabe
├── copy_task.py # 8.5.1 einfache Kopieraufgabe
└── parser_task.py # 8.5.3 ParsenaufgabeDie Inhalte, die in jedem Beispiel gelernt werden, sind wie folgt:
Einfache Kopieraufgabe ermöglicht das Verständnis der grundlegenden Funktionen des Transformers. Durch die Visualisierung von Aufmerksamkeitsmustern kann man das Funktionsprinzip des Modells klar verstehen. Zudem lernt man grundlegende Methoden zur Verarbeitung von Sequenzdaten, die Design von Tensor-Dimensionen für Batch-Verarbeitung, grundlegende Padding- und Masking-Strategien sowie den Entwurf von Task-spezifischen Verlustfunktionen.
Additionsaufgabe zeigt, wie autoregressive Erzeugung ermöglicht wird. Man kann den sequentiellen Generierungsprozess des Decoders und die Rolle der Cross-Aufmerksamkeit klar beobachten. Zusammen damit werden Tokenisierung von Zahlen, Methoden zur Erstellung gültiger Datensätze, partielle/gesamte Genauigkeitsbewertungen sowie Tests der Verallgemeinerungsleistung bei Stellenwertausweitung praktisch erlebt.
Parsenaufgabe zeigt, wie Transformer strukturelle Beziehungen lernen und darstellen. Man kann verstehen, wie die Aufmerksamkeitsmechanismen hierarchische Strukturen in Eingabesequenzen erfassen. Zudem lernt man Sequenztransformation von strukturierten Daten, Design des Token-Vokabulars, Linearisierungsstrategien für Baumstrukturen und Methoden zur Bewertung der strukturellen Genauigkeit, die bei realen Parsing-Problemen notwendig sind.
Im Folgenden ist eine Tabelle mit den zu erlernenden Inhalten in jedem Beispiel zusammengefasst.
| Beispiel | Lerninhalte |
|---|---|
| 8.5.1 einfache Kopieraufgabe (copy_task.py) | - Grundlegende Funktionen und Funktionsweise des Transformers verstehen - Visualisierung von Aufmerksamkeitsmustern - Verarbeitung von Sequenzdaten, Design von Tensor-Dimensionen für Batch-Verarbeitung - Padding- und Masking-Strategien sowie Task-spezifische Verlustfunktionen |
| 8.5.2 Additionsaufgabe (addition_task.py) | - Verständnis von autoregressiver Erzeugung - Beobachtung des sequentiellen Generierungsprozesses und der Rolle der Cross-Aufmerksamkeit - Tokenisierung von Zahlen, Methoden zur Erstellung gültiger Datensätze - Partielle/gesamte Genauigkeitsbewertungen, Tests der Verallgemeinerungsleistung bei Stellenwertausweitung |
| 8.5.3 Parsenaufgabe (parser_task.py) | - Verständnis, wie Transformer strukturelle Beziehungen lernen und darstellen - Verständnis, wie Aufmerksamkeitsmechanismen hierarchische Strukturen in Eingabesequenzen erfassen - Sequenztransformation von strukturierten Daten, Design des Token-Vokabulars - Linearisierungsstrategien für Baumstrukturen und Methoden zur Bewertung der strukturellen Genauigkeit |
8.5.1 einfache Kopieraufgabe
Das erste Beispiel ist eine Kopieraufgabe, bei der die Eingabe-Sequenz unverändert ausgegeben wird. Diese Aufgabe eignet sich gut, um das grundlegende Verhalten des Transformers zu überprüfen und Aufmerksamkeitsmuster zu visualisieren. Obwohl sie einfach erscheint, ist sie sehr nützlich für das Verständnis der Kernmechanismen des Transformers.
Datenbereitstellung
Die Daten für die Kopieraufgabe bestehen aus Sequenzen, bei denen Eingabe und Ausgabe identisch sind. Das folgende Beispiel zeigt, wie solche Daten generiert werden können.
Code
from dldna.chapter_08.transformer.examples.copy_task import explain_copy_data
explain_copy_data(seq_length=5)
=== Copy Task Data Explanation ===
Sequence Length: 5
1. Input Sequence:
Original Tensor Shape: torch.Size([1, 5])
Input Sequence: [7, 15, 2, 3, 12]
2. Target Sequence:
Original Tensor Shape: torch.Size([1, 5])
Target Sequence: [7, 15, 2, 3, 12]
3. Task Description:
- Basic task of copying the input sequence as is
- Tokens at each position are integer values between 1-19
- Input and output have the same sequence length
- Current Example: [7, 15, 2, 3, 12] → [7, 15, 2, 3, 12]create_copy_data erstellt Tensoren für das Training, bei denen Eingabe und Ausgabe identisch sind. Es generiert einen zweidimensionalen Tensor (batch_size, seq_length) für die Batch-Verarbeitung, wobei jedes Element einen ganzzahligen Wert zwischen 1 und 19 hat.
Code
def create_copy_data(batch_size: int = 32, seq_length: int = 5) -> torch.Tensor:
"""복사 태스크용 데이터 생성"""
sequences = torch.randint(1, 20, (batch_size, seq_length))
return sequences, sequencesDiese Daten in diesem Beispiel sind identisch mit tokenisierten Eingabedaten, die in der natürlichen Sprachverarbeitung und Sequenzmodellierung verwendet werden. In der Sprachverarbeitung wird jeder Token in einen eindeutigen ganzzahligen Wert konvertiert, bevor er dem Modell übergeben wird.
Modelltraining
Das Modell wird mit folgendem Code trainiert.
Code
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.copy_task import train_copy_task
seq_length = 20
config = TransformerConfig()
# Modify default values
config.vocab_size = 20 # Small vocabulary size (minimum size to represent integers 1-19)
config.hidden_size = 64 # Small hidden dimension (enough representation for a simple task)
config.num_hidden_layers = 2 # Minimum number of layers (considering the low complexity of the copy task)
config.num_attention_heads = 2 # Minimum number of heads (minimum configuration for attention from various perspectives)
config.intermediate_size = 128 # Small FFN dimension (set to twice the hidden dimension to ensure adequate transformation capacity)
config.max_position_embeddings = seq_length # Short sequence length (set to the same length as the input sequence)
model = train_copy_task(config, num_epochs=50, batch_size=40, steps_per_epoch=100, seq_length=seq_length)
=== Start Training ====
Device: cuda:0
Model saved to saved_models/transformer_copy_task.pthModelltest
Das gespeicherte Trainingsmodell wird gelesen und getestet.
Code
from dldna.chapter_08.transformer.examples.copy_task import test_copy
test_copy(seq_length=20)
=== Copy Test ===
Input: [10, 10, 2, 12, 1, 5, 3, 1, 8, 18, 2, 19, 2, 2, 8, 14, 7, 19, 5, 4]
Output: [10, 10, 2, 12, 1, 5, 3, 1, 8, 18, 2, 19, 2, 2, 8, 14, 7, 19, 5, 4]
Accuracy: TrueModell-Konfiguration
hidden_size: 64 (Entwurfsdimension des Modells, d_model).- Entwurfsdimension (d_model) in Transformers ist gleich:
- Wort-Einbettungsdimension
- Positionale Einbettungsdimension
- Aufmerksamkeitsvektordimensionen für Q, K, V
- Ausgabedimension jeder Subschicht des Encoders/Decoders
- Entwurfsdimension (d_model) in Transformers ist gleich:
intermediate_size: Größe der FFN, die größer als d_model sein sollte.
Maskierungsumsetzung
Transformers verwenden zwei Arten von Masken.
- Padding-Maske (Padding Mask): Ignoriert Padding-Tokens, die für Batchverarbeitung hinzugefügt wurden.
- In diesem Beispiel sind alle Sequenzen
seq_lengthlang, sodass keine Padding erforderlich ist; es wird jedoch zur allgemeinen Anwendung von Transformers beibehalten. - Implementieren Sie die Funktion
create_pad_maskselbst (wird intern in PyTorchsnn.Transformeroder der Hugging Facetransformers-Bibliothek implementiert).
- In diesem Beispiel sind alle Sequenzen
Code
src_mask = create_pad_mask(src).to(device)- Nachfolgende Maske (Subsequent Mask): Wird für die autoregressive Generierung des Decoders verwendet.
- Die Funktion
create_subsequent_maskerstellt eine obere Dreiecksmatrix, die Tokens nach der aktuellen Position verdeckt. - Sie stellt sicher, dass der Decoder nur auf bereits erzeugte Tokens zurückgreift, um den nächsten Token zuvorzusagen.
Code
tgt_mask = create_subsequent_mask(decoder_input.size(1)).to(device)Diese Maskierung gewährleistet die Effizienz des Batch-Verarbeitens und die Kausalität in den Sequenzen.
Design der Verlustfunktion
Die Klasse CopyLoss implementiert eine Verlustfunktion für Kopieraufgaben.
- Es wird sowohl die Genauigkeit an jeder Token-Position als auch das vollständige Übereinstimmen der gesamten Sequenz berücksichtigt.
- Die Genauigkeit, der Verlustwert und die vorhergesagten/realen Werte werden detailliert überwacht, um den Fortschritt des Trainings genau zu verfolgen.
Code
class CopyLoss(nn.Module):
def forward(self, outputs: torch.Tensor, target: torch.Tensor,
print_details: bool = False) -> Tuple[torch.Tensor, float]:
batch_size = outputs.size(0)
predictions = F.softmax(outputs, dim=-1)
target_one_hot = F.one_hot(target, num_classes=outputs.size(-1)).float()
loss = -torch.sum(target_one_hot * torch.log(predictions + 1e-10)) / batch_size
with torch.no_grad():
pred_tokens = predictions.argmax(dim=-1)
exact_match = (pred_tokens == target).all(dim=1).float()
match_rate = exact_match.mean().item()- Nur die Kreuzentropie ist unzureichend: Genauigkeit einzelner Token + Bewertung der Übereinstimmung des gesamten Sequenz.
- Modell zur genauen Lernung der Reihenfolge anleiten.
Beispielfunktionsweise (batch_size=2, sequence_length=3, vocab_size=5):
- Modellausgabe (Logits)
Code
# Example: batch_size=2, sequence_length=3, vocab_size=5 (example is vocab_size=20)
# 1. Model Output (logits)
outputs = [
# First batch
[[0.9, 0.1, 0.0, 0.0, 0.0], # First position: token 0 has the highest probability
[0.1, 0.8, 0.1, 0.0, 0.0], # Second position: token 1 has the highest probability
[0.0, 0.1, 0.9, 0.0, 0.0]], # Third position: token 2 has the highest probability
# Second batch
[[0.8, 0.2, 0.0, 0.0, 0.0],
[0.1, 0.7, 0.2, 0.0, 0.0],
[0.1, 0.1, 0.8, 0.0, 0.0]]
]- Tatsächliches Target
Code
# 2. Actual Target
target = [
[0, 1, 2], # Correct sequence for the first batch
[0, 1, 2] # Correct sequence for the second batch
]- Verlustberechnungsprozess
predictions = softmax(outputs)(schon oben in Wahrscheinlichkeiten konvertiert)targetin One-Hot-Vektor konvertieren
Code
# 3. Loss Calculation Process
# predictions = softmax(outputs) (already converted to probabilities above)
# Convert target to one-hot vectors:
target_one_hot = [
[[1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0]], # First batch
[[1,0,0,0,0], [0,1,0,0,0], [0,0,1,0,0]] # Second batch
]- Genauigkeit berechnen
Code
# 4. Accuracy Calculation
pred_tokens = [
[0, 1, 2], # First batch prediction
[0, 1, 2] # Second batch prediction
]- Übereinstimmung der gesamten Sequenz:
exact_match = [True, True](beide Batches sind korrekt) - Durchschnittliche Genauigkeit:
match_rate = 1.0(100%)
- Endgültiger Verlustwert: Mittelwert der Kreuzentropie
Code
# Exact sequence match
exact_match = [True, True] # Both batches match exactly
match_rate = 1.0 # Average accuracy 100%
# The final loss value is the average of the cross-entropy
# loss = -1/2 * (log(0.9) + log(0.8) + log(0.9) + log(0.8) + log(0.7) + log(0.8))Aufmerksamkeitsvisualisierung
Durch die Visualisierung der Aufmerksamkeit kann man das Verhalten des Transformers anschaulich verstehen.
Code
from dldna.chapter_08.transformer.examples.copy_task import visualize_attention
visualize_attention(seq_length=20)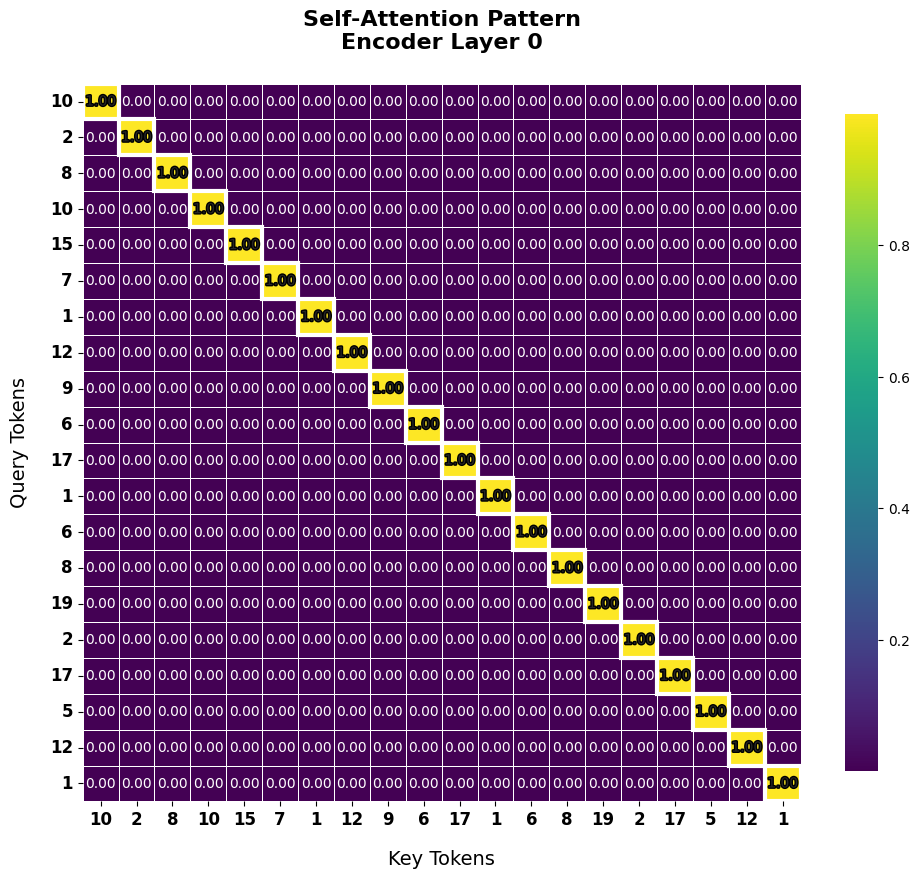
Jede Eingabetoken wird überprüft, wie es mit Tokens an anderen Positionen interagiert.
Durch dieses Kopier-Task-Beispiel haben wir den Kernmechanismus des Transformers untersucht. Im nächsten Beispiel (Additionsproblem) werden wir sehen, wie der Transformer arithmetische Regeln wie die Beziehungen zwischen Zahlen und das Übertragen lernt.
8.5.2 Stellenweise Additionsaufgabe
Das zweite Beispiel ist eine Additionsaufgabe, bei der zwei Zahlen addiert werden. Diese Aufgabe eignet sich, um die autoregressiven Generierungsfähigkeiten des Transformers und den sequenziellen Berechnungsprozess des Decoders zu verstehen. Durch das Rechnen mit Überträgen kann beobachtet werden, wie der Transformer die Beziehungen zwischen Zahlen lernt.
Daten vorbereiten
Die Daten für die Additionsaufgabe werden in create_addition_data() generiert.
Code
def create_addition_data(batch_size: int = 32, max_digits: int = 3) -> Tuple[torch.Tensor, torch.Tensor]:
"""Create addition dataset"""
max_value = 10 ** max_digits - 1
num1 = torch.randint(0, max_value // 2 + 1, (batch_size,))
num2 = torch.randint(0, max_value // 2 + 1, (batch_size,))
result = num1 + num2
[See source below]- Erzeuge zwei Zahlen, deren Summe die angegebene Anzahl von Stellen nicht überschreitet.
- Eingabe: Zwei Zahlen + ‘+’ Zeichen.
- Enthält Validierung der Stellenbegrenzung.
Code
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.addition_task import explain_addition_data
explain_addition_data()
=== Addition Data Explanation ====
Maximum Digits: 3
1. Input Sequence:
Original Tensor Shape: torch.Size([1, 7])
First Number: 153 (Indices [np.int64(1), np.int64(5), np.int64(3)])
Plus Sign: '+' (Index 10)
Second Number: 391 (Indices [np.int64(3), np.int64(9), np.int64(1)])
Full Input: [1, 5, 3, 10, 3, 9, 1]
2. Target Sequence:
Original Tensor Shape: torch.Size([1, 3])
Actual Sum: 544
Target Sequence: [5, 4, 4]Modelltraining und -test
Code
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.addition_task import train_addition_task
config = TransformerConfig()
config.vocab_size = 11
config.hidden_size = 256
config.num_hidden_layers = 3
config.num_attention_heads = 4
config.intermediate_size = 512
config.max_position_embeddings = 10
model = train_addition_task(config, num_epochs=10, batch_size=128, steps_per_epoch=300, max_digits=3)Epoch 0, Average Loss: 6.1352, Final Accuracy: 0.0073, Learning Rate: 0.000100
Epoch 5, Average Loss: 0.0552, Final Accuracy: 0.9852, Learning Rate: 0.000100
=== Loss Calculation Details (Step: 3000) ===
Predicted Sequences (First 10): tensor([[6, 5, 4],
[5, 3, 3],
[1, 7, 5],
[6, 0, 6],
[7, 5, 9],
[5, 2, 8],
[2, 8, 1],
[3, 5, 8],
[0, 7, 1],
[6, 2, 1]], device='cuda:0')
Actual Target Sequences (First 10): tensor([[6, 5, 4],
[5, 3, 3],
[1, 7, 5],
[6, 0, 6],
[7, 5, 9],
[5, 2, 8],
[2, 8, 1],
[3, 5, 8],
[0, 7, 1],
[6, 2, 1]], device='cuda:0')
Exact Match per Sequence (First 10): tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.], device='cuda:0')
Calculated Loss: 0.0106
Calculated Accuracy: 1.0000
========================================
Model saved to saved_models/transformer_addition_task.pthNach dem Lernen wird das gespeicherte Modell geladen und die Tests durchgeführt.
Code
from dldna.chapter_08.transformer.examples.addition_task import test_addition
test_addition(max_digits=3)
Addition Test (Digits: 3):
310 + 98 = 408 (Actual Answer: 408)
Correct: TrueModellkonfiguration
Die Transformer-Konfiguration für die Additionsaufgabe ist wie folgt:
Code
config = TransformerConfig()
config.vocab_size = 11 # 0-9 digits + '+' symbol
config.hidden_size = 256 # Larger hidden dimension than copy task (sufficient capacity for learning arithmetic operations)
config.num_hidden_layers = 3 # Deeper layers (hierarchical feature extraction for handling carry operations)
config.num_attention_heads = 4 # Increased number of heads (learning relationships between different digit positions)
config.intermediate_size = 512 # FFN dimension: should be larger than hidden_size.Maskierungsumsetzung
In der Additionsaufgabe ist ein Padding-Mask erforderlich. Da die Stellenanzahl der Eingabezahlen variieren kann, müssen die Padding-Positionen ignoriert werden, um eine genaue Berechnung durchzuführen.
Code
def _number_to_digits(number: torch.Tensor, max_digits: int) -> torch.Tensor:
"""숫자를 자릿수 시퀀스로 변환하며 패딩 적용"""
return torch.tensor([[int(d) for d in str(n.item()).zfill(max_digits)]
for n in number])Die Operation dieser Methode ist spezifisch wie folgt definiert.
Code
number = torch.tensor([7, 25, 348])
max_digits = 3
result = _number_to_digits(number, max_digits)
# 입력: [7, 25, 348]
# 과정:
# 7 -> "7" -> "007" -> [0,0,7]
# 25 -> "25" -> "025" -> [0,2,5]
# 348 -> "348" -> "348" -> [3,4,8]
# 결과: tensor([[0, 0, 7],
# [0, 2, 5],
# [3, 4, 8]])Verlustfunktionen-Design
AdditionLoss Klasse implementiert die Verlustfunktion für Additionsaufgaben.
- Im Gegensatz zu Kopieraufgaben, werden Stellenweise Genauigkeit und Gesamtantwortgenauigkeit getrennt bewertet.
Code
class AdditionLoss(nn.Module):
def forward(self, outputs: torch.Tensor, target: torch.Tensor,
print_details: bool = False) -> Tuple[torch.Tensor, float]:
batch_size = outputs.size(0)
predictions = F.softmax(outputs, dim=-1)
target_one_hot = F.one_hot(target, num_classes=outputs.size(-1)).float()
loss = -torch.sum(target_one_hot * torch.log(predictions + 1e-10)) / batch_size
with torch.no_grad():
pred_digits = predictions.argmax(dim=-1)
exact_match = (pred_digits == target).all(dim=1).float()
match_rate = exact_match.mean().item()- Verlustberechnung: Genauigkeit der Vorhersage für jede Ziffer + Überprüfung der Übertrag Genauigkeit.
- Nicht nur einfache Ziffernzuordnung, sondern das Lernen von Additionssregeln anregen.
AdditionLoss Funktionsweise (Beispiel: batch_size=2, sequence_length=3, vocab_size=10)
Code
outputs = [
[[0.1, 0.8, 0.1, 0, 0, 0, 0, 0, 0, 0], # 첫 번째 자리
[0.1, 0.1, 0.7, 0.1, 0, 0, 0, 0, 0, 0], # 두 번째 자리
[0.8, 0.1, 0.1, 0, 0, 0, 0, 0, 0, 0]] # 세 번째 자리
] # 첫 번째 배치
target = [
[1, 2, 0] # 실제 정답: "120"
] # 첫 번째 배치
# 1. softmax는 이미 적용되어 있다고 가정 (outputs)
# 2. target을 원-핫 인코딩으로 변환
target_one_hot = [
[[0,1,0,0,0,0,0,0,0,0], # 1
[0,0,1,0,0,0,0,0,0,0], # 2
[1,0,0,0,0,0,0,0,0,0]] # 0
]
# 3. 손실 계산
# -log(0.8) - log(0.7) - log(0.8) = 0.223 + 0.357 + 0.223 = 0.803
loss = 0.803 / batch_size
# 4. 정확도 계산
pred_digits = [1, 2, 0] # argmax 적용
exact_match = True # 모든 자릿수가 일치
match_rate = 1.0 # 배치의 평균 정확도Die Ausgabe des Transformer-Decoder wird am letzten Layer in vocab_size linear transformiert, daher haben die Logits eine Dimension von vocab_size.
Im nächsten Abschnitt werden wir untersuchen, wie der Transformer komplexe strukturelle Beziehungen durch das Parsing-Task lernt.
8.5.3 Parser-Aufgabe
Das letzte Beispiel ist die Implementierung einer Parser-Aufgabe. Diese Aufgabe besteht darin, Ausdrücke in einen Parse-Baum zu konvertieren, wodurch ein Beispiel gegeben wird, um zu überprüfen, wie gut Transformatoren strukturelle Informationen verarbeiten können.
Erklärung des Datenvorbereitungsprozesses
Die Trainingsdaten für die Parser-Aufgabe werden durch folgende Schritte erstellt:
- Ausdruckserstellung:
- Die
generate_random_expression()Funktion wird verwendet, um Variablen (x, y, z), Operatoren (+, -, *, /) und Zahlen (0-9) zu kombinieren, um einfache Ausdrücke wie “x=1+2” zu erstellen.
- Die
- Parse-Baum-Konvertierung:
- Die
parse_to_tree()Funktion wird verwendet, um die generierten Ausdrücke in verschachtelte Listenformen von Parse-Bäumen wie['ASSIGN', 'x', ['ADD', '1', '2']]zu konvertieren. Dieser Baum repräsentiert die hierarchische Struktur des Ausdrucks.
- Die
- Tokenisierungsverarbeitung:
- Die Ausdrücke und Parse-Bäume werden jeweils in Integer-Sequenzen konvertiert.
- Jedes Token wird gemäß der vordefinierten
TOKEN_DICTauf eine eindeutige Ganzzahl-ID abgebildet.
Code
def create_addition_data(batch_size: int = 32, max_digits: int = 3) -> Tuple[torch.Tensor, torch.Tensor]:
"""Create addition dataset"""
max_value = 10 ** max_digits - 1
# Generate input numbers
num1 = torch.randint(0, max_value // 2 + 1, (batch_size,))
num2 = torch.randint(0, max_value // 2 + 1, (batch_size,))
result = num1 + num2
# [이하 생략]- Generieren Sie zwei Zahlen, deren Summe die angegebene Anzahl von Stellen nicht überschreitet.
- Eingabe: Zwei Zahlen + ‘+’ Symbol.
- Enthält eine Validierung der Stellenbegrenzung.
Beschreibung der LernDaten Das folgende beschreibt die Struktur der LernDaten. Es zeigt, wie sich Ausdrücke und Tokenisierungen in bestimmte Werte verwandeln.
Code
from dldna.chapter_08.transformer.examples.parser_task import explain_parser_data
explain_parser_data()
=== Parsing Data Explanation ===
Max Tokens: 5
1. Input Sequence:
Original Tensor Shape: torch.Size([1, 5])
Expression: x = 4 + 9
Tokenized Input: [11, 1, 17, 2, 22]
2. Target Sequence:
Original Tensor Shape: torch.Size([1, 5])
Parse Tree: ['ASSIGN', 'x', 'ADD', '4', '9']
Tokenized Output: [6, 11, 7, 17, 22]Erklärung des Parsierungsbeispiels
Wenn der folgende Code ausgeführt wird, werden die Erklärungen in einer Reihenfolge angezeigt, die es erleichtert zu verstehen, wie die Daten des Parsierungsbeispiels strukturiert sind.
Code
from dldna.chapter_08.transformer.examples.parser_task import show_parser_examples
show_parser_examples(num_examples=3 )
=== Generating 3 Parsing Examples ===
Example 1:
Generated Expression: y=7/7
Parse Tree: ['ASSIGN', 'y', ['DIV', '7', '7']]
Expression Tokens: [12, 1, 21, 5, 21]
Tree Tokens: [6, 12, 10, 21, 21]
Padded Expression Tokens: [12, 1, 21, 5, 21]
Padded Tree Tokens: [6, 12, 10, 21, 21]
Example 2:
Generated Expression: x=4/3
Parse Tree: ['ASSIGN', 'x', ['DIV', '4', '3']]
Expression Tokens: [11, 1, 18, 5, 17]
Tree Tokens: [6, 11, 10, 18, 17]
Padded Expression Tokens: [11, 1, 18, 5, 17]
Padded Tree Tokens: [6, 11, 10, 18, 17]
Example 3:
Generated Expression: x=1*4
Parse Tree: ['ASSIGN', 'x', ['MUL', '1', '4']]
Expression Tokens: [11, 1, 15, 4, 18]
Tree Tokens: [6, 11, 9, 15, 18]
Padded Expression Tokens: [11, 1, 15, 4, 18]
Padded Tree Tokens: [6, 11, 9, 15, 18]
Modelltraining und -test
Code
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.parser_task import train_parser_task
config = TransformerConfig()
config.vocab_size = 25 # Adjusted to match the token dictionary size
config.hidden_size = 128
config.num_hidden_layers = 3
config.num_attention_heads = 4
config.intermediate_size = 512
config.max_position_embeddings = 10
model = train_parser_task(config, num_epochs=6, batch_size=64, steps_per_epoch=100, max_tokens=5, print_progress=True)
=== Start Training ===
Device: cuda:0
Batch Size: 64
Steps per Epoch: 100
Max Tokens: 5
Epoch 0, Average Loss: 6.3280, Final Accuracy: 0.2309, Learning Rate: 0.000100
=== Prediction Result Samples ===
Input: y = 8 * 8
Prediction: ['ASSIGN', 'y', 'MUL', '8', '8']
Truth: ['ASSIGN', 'y', 'MUL', '8', '8']
Result: Correct
Input: z = 6 / 5
Prediction: ['ASSIGN', 'z', 'DIV', '8', 'a']
Truth: ['ASSIGN', 'z', 'DIV', '6', '5']
Result: Incorrect
Epoch 5, Average Loss: 0.0030, Final Accuracy: 1.0000, Learning Rate: 0.000100
=== Prediction Result Samples ===
Input: z = 5 - 6
Prediction: ['ASSIGN', 'z', 'SUB', '5', '6']
Truth: ['ASSIGN', 'z', 'SUB', '5', '6']
Result: Correct
Input: y = 9 + 9
Prediction: ['ASSIGN', 'y', 'ADD', '9', '9']
Truth: ['ASSIGN', 'y', 'ADD', '9', '9']
Result: Correct
Model saved to saved_models/transformer_parser_task.pthTest durchführen.
Code
from dldna.chapter_08.transformer.config import TransformerConfig
from dldna.chapter_08.transformer.examples.parser_task import test_parser
test_parser()
=== Parser Test ===
Input Expression: x = 8 * 3
Predicted Parse Tree: ['ASSIGN', 'x', 'MUL', '8', '3']
Actual Parse Tree: ['ASSIGN', 'x', 'MUL', '8', '3']
Correct: True
=== Additional Tests ===
Input: x=1+2
Predicted Parse Tree: ['ASSIGN', 'x', 'ADD', '2', '3']
Input: y=3*4
Predicted Parse Tree: ['ASSIGN', 'y', 'MUL', '4', '5']
Input: z=5-1
Predicted Parse Tree: ['ASSIGN', 'z', 'SUB', '6', '2']
Input: x=2/3
Predicted Parse Tree: ['ASSIGN', 'x', 'DIV', '3', '4']Modell-Einstellungen - vocab_size: 25 (Größe des Token-Wörterbuchs) - hidden_size: 128 - num_hidden_layers: 3 - num_attention_heads: 4 - intermediate_size: 512 - max_position_embeddings: 10 (Maximale Anzahl von Tokens)
Verlustfunktionsentwurf
Die Verlustfunktion für die Parser-Aufgabe verwendet den Kreuzentropieverlust.
- Ausgabetransformation: Die Ausgabe des Modells wird mithilfe der Softmax-Funktion in Wahrscheinlichkeiten transformiert.
- Zieltransformation: Die Ziel-Sequenz (Richtige Antworten) wird in One-Hot-Codierung umgewandelt.
- Verlustberechnung: Der durchschnittliche negative Logarithmus der Wahrscheinlichkeiten wird berechnet, um den Verlust zu ermitteln.
- Genauigkeit: Die Genauigkeit wird dadurch berechnet, ob die vorhergesagte Sequenz vollständig mit der richtigen Sequenz übereinstimmt. Dies spiegelt die Eigenschaften dieser Aufgabe wider, bei der der Parse-Baum exakt erstellt werden muss.
Beispiel für den Ablauf der Verlustfunktion
Code
# Example input values (batch_size=2, sequence_length=4, vocab_size=5)
# vocab = {'=':0, 'x':1, '+':2, '1':3, '2':4}
outputs = [
# First batch: prediction probabilities for "x=1+2"
[[0.1, 0.7, 0.1, 0.1, 0.0], # predicting x
[0.8, 0.1, 0.0, 0.1, 0.0], # predicting =
[0.1, 0.0, 0.1, 0.7, 0.1], # predicting 1
[0.0, 0.1, 0.8, 0.0, 0.1]], # predicting +
# Second batch: prediction probabilities for "x=2+1"
[[0.1, 0.8, 0.0, 0.1, 0.0], # predicting x
[0.7, 0.1, 0.1, 0.0, 0.1], # predicting =
[0.1, 0.0, 0.1, 0.1, 0.7], # predicting 2
[0.0, 0.0, 0.9, 0.1, 0.0]] # predicting +
]
target = [
[1, 0, 3, 2], # Actual answer: "x=1+"
[1, 0, 4, 2] # Actual answer: "x=2+"
]
# Convert target to one-hot encoding
target_one_hot = [
[[0,1,0,0,0], # x
[1,0,0,0,0], # =
[0,0,0,1,0], # 1
[0,0,1,0,0]], # +
[[0,1,0,0,0], # x
[1,0,0,0,0], # =
[0,0,0,0,1], # 2
[0,0,1,0,0]] # +
]
# Loss calculation (first batch)
# -log(0.7) - log(0.8) - log(0.7) - log(0.8) = 0.357 + 0.223 + 0.357 + 0.223 = 1.16
# Loss calculation (second batch)
# -log(0.8) - log(0.7) - log(0.7) - log(0.9) = 0.223 + 0.357 + 0.357 + 0.105 = 1.042
# Total loss
loss = (1.16 + 1.042) / 2 = 1.101
# Accuracy calculation
pred_tokens = [
[1, 0, 3, 2], # First batch prediction
[1, 0, 4, 2] # Second batch prediction
]
exact_match = [True, True] # Both batches match exactly
match_rate = 1.0 # Overall accuracyBislang konnten wir durch Beispiele erkennen, dass Transformer strukturelle Informationen effektiv verarbeiten können.
Fazit
In Kapitel 8 haben wir den Hintergrund der Entstehung von Transformatoren und ihre Kernkomponenten eingehend untersucht. Wir haben die Herausforderungen betrachtet, denen sich Forscher gegenübersahen, um die Grenzen von RNN-basierten Modellen zu überwinden, die Entdeckung und Entwicklung des Aufmerksamkeitsmechanismus sowie die Konkretisierung der Kernideen der Transformer durch die Trennung der Q, K, V-Vektoraum und die parallele Verarbeitung und das Erfassen von Kontextinformationen aus verschiedenen Perspektiven mittels Multi-Head-Aufmerksamkeit. Darüber hinaus haben wir die Positionscodierung zur effektiven Repräsentation von Ortsinformationen, raffinierte Maskierungsstrategien zur Verhinderung von Informationsverlust und die detaillierte Analyse der Encoder-Decoder-Struktur sowie der Funktion und des Arbeitsmechanismus ihrer Komponenten untersucht.
Durch drei Beispiele (einfache Kopie, Addition von Stellenwerten, Parser) konnten wir intuitiv verstehen, wie Transformer tatsächlich funktionieren und welche Rolle die einzelnen Komponenten spielen. Diese Beispiele zeigen die grundlegenden Funktionen der Transformatoren, ihre fähigkeit zur autoregressiven Generierung und Verarbeitung struktureller Informationen und bilden das Grundwissen für die Anwendung von Transformatoren in realen Natürlichsprachverarbeitungsproblemen.
Im nächsten Schritt werden wir in Kapitel 9 die Entwicklung der Transformer seit der Veröffentlichung des Papers “Attention is All You Need” verfolgen. Wir werden sehen, wie verschiedene transformerbasierte Modelle wie BERT und GPT entstanden sind und welche Innovationen diese Modelle über die Natürlichsprachverarbeitung hinaus in Bereichen wie Computer Vision und Spracherkennung gebracht haben.
Übungsaufgaben
Grundlegende Aufgaben
- Welche beiden Hauptvorteile haben Transformatoren im Vergleich zu RNNs?
- Was ist die Kernidee des Attention-Mechanismus, und welche Vorteile bietet dies?
- Welche Vorteile bietet Multi-Head Attention verglichen mit Self-Attention?
- Warum sind Positional Encodings notwendig, und wie werden Positionsinformationen dargestellt?
- Welche Aufgaben übernehmen der Encoder und der Decoder in einem Transformer?
Anwendungsaufgaben
- Textzusammenfassung: Entwerfen Sie ein Transformer-Modell, das eine gegebene lange Texteingabe in einen kurzen Zusammenfassungsabsatz umwandelt, und erklären Sie, welche Bewertungskriterien verwendet werden können, um die Leistung des Modells zu messen.
- Analyse von Frage-Antwort-Systemen: Beschreiben Sie schrittweise den Prozess, wie ein transformerbasiertes Frage-Antwort-System eine korrekte Antwort auf eine gegebene Frage findet, und analysieren Sie die zentrale Rolle des Attention-Mechanismus in diesem Prozess.
- Untersuchung von Anwendungsbeispielen in anderen Domänen: Untersuchen Sie mindestens zwei Fälle, in denen Transformatoren erfolgreich in Domänen außerhalb der natürlichen Sprachverarbeitung (wie Bilder, Audio, Graphen) eingesetzt wurden, und erklären Sie, wie sie genutzt wurden und welche Vorteile sie bieten.
Fortgeschrittene Aufgaben
- Vergleichende Analyse von Ansätzen zur Verbesserung der Berechnungskomplexität: Untersuchen Sie mindestens zwei Methoden (z.B. Reformer, Performer, Longformer), die vorgeschlagen wurden, um die Berechnungskomplexität von Transformatoren zu verbessern, und vergleichen Sie die Kernideen, Vor- und Nachteile sowie mögliche Anwendungsszenarien dieser Methoden.
- Vorschlag und Evaluierung neuer Architekturen: Schlagen Sie eine transformerbasierte neue Architektur vor, die für ein spezifisches Problem (z.B. langfristige Textklassifikation, mehrsprachige Übersetzung) optimiert ist, und erklären Sie theoretisch und experimentell, welche Vorteile sie gegenüber bestehenden Transformer-Modellen bietet.
- Analyse ethischer und gesellschaftlicher Auswirkungen sowie Entwicklungsansätze: Analysieren Sie die positiven und negativen Auswirkungen der Entwicklung großer Sprachmodelle basierend auf Transformatoren (z.B. GPT-3, BERT) auf die Gesellschaft und schlagen Sie technische und politische Ansätze vor, um insbesondere die negativen Auswirkungen wie Verzerrungen, Falschinformationen und Arbeitsplatzverluste zu mildern.
Klicken Sie hier, um den Inhalt anzuzeigen (Lösungen zu Übungsproblemen)
Übungsaufgaben Lösungen
Grundlegende Aufgaben
Vorteile von Transformatoren im Vergleich zu RNNs: Transformatoren haben zwei Hauptvorteile gegenüber RNNs: parallele Verarbeitung und die Lösung des Problems langer Abhängigkeiten. RNNs verarbeiten sequenziell, was sie langsam macht, während Transformatoren durch Aufmerksamkeit alle Wörter gleichzeitig verarbeiten, was GPU-parallelverarbeitung ermöglicht und das Lern Tempo beschleunigt. Zudem führen RNNs bei langen Sequenzen zu Informationsverlust, während Transformatoren durch Selbst-Aufmerksamkeit die Beziehungen zwischen Wörtern direkt berechnen und wichtige Informationen unabhängig von der Distanz beibehalten.
Kern & Effekte des Aufmerksamkeitsmechanismus: Die Aufmerksamkeit berechnet, wie wichtig jeder Teil der Eingabe-Sequenz für die Erzeugung der Ausgabe-Sequenz ist. Der Dekoder achtet beim Vorhersagen von Ausgabewörtern nicht gleichmäßig auf die gesamte Eingabe, sondern legt mehr “Fokus” auf relevantere Teile, um den Kontext besser zu verstehen und präzisere Vorhersagen zu treffen.
Vorteile des Multi-Head-Aufmerksamkeitsmechanismus: Der Multi-Head-Aufmerksamkeitsmechanismus führt mehrere Selbst-Aufmerksamkeitsoperationen parallel durch. Jeder Kopf lernt die Beziehungen zwischen Wörtern in der Eingabe-Sequenz aus unterschiedlichen Perspektiven, was dem Modell hilft, reichhaltigere und vielfältigere Kontextinformationen zu erfassen. (ähnlich wie mehrere Detektive, die jeweils ein Fachgebiet haben und zusammenarbeiten)
Notwendigkeit & Methode der Positionalcodierung: Da Transformatoren nicht sequenziell verarbeitet werden, müssen sie den Ortinformationen der Wörter informiert werden. Die Positions-Codierung funktioniert, indem ein Vektor mit Ortsinformationen zu jedem Wort-Vektor hinzugefügt wird. Auf diese Weise können Transformatoren nicht nur die Bedeutung des Wortes, sondern auch dessen Position im Satz berücksichtigen, um den Kontext zu verstehen. Meistens werden Sinus-Kosinus-Funktionen verwendet, um Ortsinformationen darzustellen.
Rolle von Encoder & Decoder: Transformatoren haben eine Encoder-Decoder-Architektur. Der Encoder erhält die Eingabe-Sequenz und erzeugt eine Darstellung (Kontext-Vektor), die den Kontext jedes Worts berücksichtigt. Der Decoder nimmt diese Kontextinformationen auf, um die Ausgabe-Sequenz zu generieren.
Anwendungsbeispiele
- Analyse eines Frage-Antwort-Systems: Ein transformer-basiertes Frage-Antwort-System führt den Prozess der Identifizierung der richtigen Antwort in einem Dokument für eine gegebene Frage wie folgt durch:
- Die Frage und das Dokument werden jeweils dem Transformer-Encoder eingegeben, um Einbettungsvektoren zu erhalten.
- Die Aufmerksamkeitsgewichte zwischen den Fragen-Einbettungen und den Dokument-Einbettungen werden berechnet (um zu bestimmen, welche Wörter in der Frage mit welchen Wörtern im Dokument zusammenhängen).
- Mithilfe dieser Aufmerksamkeitsgewichte wird ein gewichteter Durchschnitt der Dokument-Einbettungen berechnet und als Kontext-Vektor für die Frage verwendet.
- Basierend auf diesem Kontext-Vektor werden der Start- und Endpunkt der Antwort vorhergesagt, um die endgültige Antwort zu extrahieren. In diesem Prozess spielt der Aufmerksamkeitsmechanismus eine entscheidende Rolle bei der Identifizierung der bedeutsamsten Teile des Dokuments im Verhältnis zur Frage.
- Analyse eines Fragen-Antwort-Systems: Ein transformer-basiertes Fragen-Antwort-System führt den Prozess der Identifizierung der richtigen Antwort in einem Dokument für eine gegebene Frage wie folgt durch:
- Die Frage und das Dokument werden jeweils dem Transformer-Encoder eingegeben, um Einbettungsvektoren zu erhalten.
- Die Aufmerksamkeitsgewichte zwischen den Fragen-Einbettungen und den Dokument-Einbettungen werden berechnet (um zu bestimmen, welche Wörter in der Frage mit welchen Wörtern im Dokument zusammenhängen).
- Mithilfe dieser Aufmerksamkeitsgewichte wird ein gewichteter Durchschnitt der Dokument-Einbettungen berechnet und als Kontext-Vektor für die Frage verwendet.
- Basierend auf diesem Kontext-Vektor werden der Start- und Endpunkt der Antwort vorhergesagt, um die endgültige Antwort zu extrahieren. In diesem Prozess spielt der Aufmerksamkeitsmechanismus eine entscheidende Rolle bei der Identifizierung der bedeutsamsten Teile des Dokuments im Verhältnis zur Frage.
- Anwendungsfälle in anderen Domänen untersuchen:
- Bild: Vision Transformer (ViT) teilt ein Bild in mehrere Patchs auf und verarbeitet jeden Patch wie eine Eingabe-Sequenz für den Transformer, um leistungsfähige Ergebnisse bei Aufgaben wie Bildklassifizierung und Objekterkennung zu erzielen. Dies zeigt, dass Transformer nicht nur sequenzielle Daten, sondern auch zweidimensionale Daten wie Bilder effektiv verarbeiten können.
- Sprache: Conformer kombiniert CNNs und Transformatoren, um hohe Genauigkeit in der Spracherkennung zu erzielen. Durch die effektive Modellierung sowohl lokaler als auch globaler Merkmale von Sprachsignalen konnte die Leistung der Spracherkennung verbessert werden.
Vertiefende Aufgaben
Vergleich und Analyse von Ansätzen zur Verbesserung der Berechnungskomplexität:
Transformer haben aufgrund des Selbst-Aufmerksamkeits-Mechanismus eine quadratische Berechnungskomplexität in Bezug auf die Länge der Eingabe-Sequenz. Es wurden verschiedene Methoden vorgeschlagen, um dies zu verbessern.
- Reformer: Locality-Sensitive Hashing (LSH) Attention wird verwendet, um die Ähnlichkeit zwischen Query und Key approximativ zu berechnen. LSH ist eine Hashtechnik, die ähnliche Vektoren in den gleichen Bucket zuordnet, wodurch die Berechnung von Aufmerksamkeit für die gesamte Sequenz vermieden wird und sich die Berechnung nur auf nahe Tokens konzentriert. Reformer kann den Speicherverbrauch und die Berechnungszeit erheblich reduzieren, aber aufgrund der approximativen Berechnungen durch LSH kann die Genauigkeit leicht nachlassen.
- Longformer: Sliding Window Attention und Global Attention werden kombiniert, um lange Sequenzen effizient zu verarbeiten. Jedes Token führt nur Aufmerksamkeit auf Tokens in einem festen Fenster um es herum aus, während bestimmte Tokens (z.B. Satzanfang-Token) die gesamte Sequenz abtasten. Longformer ist schnell und speichereffizient bei der Verarbeitung langer Sequenzen, aber die Leistung kann von der Fenstergröße abhängen.
Vorschlag und Evaluation neuer Architekturen:
- Problemdefinition: Bei der Klassifizierung längerer Texte ist die Berechnungskomplexität bestehender Transformatoren hoch, und es ist schwierig, langfristige Abhängigkeiten zu erfassen.
- Architekturvorschlag: Der Text wird in mehrere Segmente aufgeteilt, und für jedes Segment wird ein Transformer-Encoder angewendet, um Segment-Embeddings zu erhalten. Danach werden diese Segment-Embeddings erneut einem Transformer-Encoder eingegeben, um eine Darstellung des gesamten Textes zu erhalten, die dann zur Klassifizierung verwendet wird.
- Theoretische Vorteile: Durch die hierarchische Struktur können langfristige Abhängigkeiten effektiv erfasst und die Berechnungskomplexität reduziert werden.
- Experimentdesign: Es werden lange Textklassifikations-Datensätze wie der IMDB-Filmebewertungsdatensatz verwendet, um die Leistung (Genauigkeit, F1-Score) des vorgeschlagenen Architekturmodells mit bestehenden Transformer-Modellen (z.B. BERT) zu vergleichen. Darüber hinaus wird die Leistungsänderung bei Variation der Textlänge und Segmentgröße analysiert, um die Effektivität des vorgeschlagenen Architekturmodells zu überprüfen.
Analyse ethischer und gesellschaftlicher Auswirkungen sowie Vorschläge zur Reaktion: Die Entwicklung von großmaßstabsprachmodellen auf Basis von Transformatoren (z.B. GPT-3, BERT) kann verschiedene positive und negative Auswirkungen auf die Gesellschaft haben.
- Positive Auswirkungen: Kommunikationsbarrieren können durch automatisches Übersetzen, Chatbots, virtuelle Assistenten usw. gesenkt werden, wodurch der Zugang zu Informationen verbessert wird. Darüber hinaus kann die Produktivität durch InhaltsGenerierung, CodeGenerierung, automatische Zusammenfassungen usw. gesteigert und Innovation in neuen Bereichen wie der Wissenschaftsforschung (z.B. Vorhersage von Proteinstrukturen), medizinischer Diagnostik etc. beschleunigt werden.
- Negative Auswirkungen: Diese Modelle können Verzerrungen im Trainingsdatensatz (Geschlecht, Ethnie, Religion usw.) lernen und diskriminierende Ergebnisse erzeugen. Böswillige Nutzer können große Mengen an Fake News generieren, um öffentliche Meinung zu manipulieren oder den Ruf bestimmter Individuen/Gruppen zu schädigen. Zudem könnte die automatisierte Texterstellung, -übersetzung und Kundenbetreuung Arbeitsplätze in betroffenen Berufen verringern und Probleme wie Verletzungen der Privatsphäre und Urheberrechtsverstöße verursachen.
- Mögliche Gegenmaßnahmen: Um diese negativen Auswirkungen zu mildern, sind technische und politische Anstrengungen erforderlich, darunter die Beseitigung von Datenverzerrungen, die Entwicklung von Techniken zur Erkennung von Fake News, gesellschaftliche Diskussionen und Vorbereitung von Wiederausbildungsprogrammen im Zusammenhang mit Arbeitsplatzveränderungen infolge der Automatisierung, Stärkung der Transparenz und Verantwortlichkeit von Algorithmen sowie die Einführung ethischer Leitlinien.
Referenzmaterialien
- Attention is All You Need (Vaswani et al., 2017) - Ursprüngliche Transformer-Paper
- The Annotated Transformer (Harvard NLP) - Detaillierte Erklärung des Transformers mit PyTorch-Implementierung
- The Illustrated Transformer (Jay Alammar) - Visuelle Erklärung des Transformers
- Transformer: A Novel Neural Network Architecture for Language Understanding (Google AI Blog) - Einführung in den Transformer
- The Transformer Family (Lilian Weng) - Vorstellung verschiedener Transformer-Varianten
- BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding (Devlin et al., 2018) - Einführung in BERT
- GPT-3: Language Models are Few-Shot Learners (Brown et al., 2020) - Einführung in GPT-3
- Hugging Face Transformers - Bereitstellung verschiedener Transformer-Modelle und Tools
- TensorFlow Transformer Tutorial - Tutorial zur Implementierung von Transformers mit TensorFlow
- PyTorch Transformer Documentation - Dokumentation der Transformer-Module in PyTorch
- Visualizing Attention in Transformer-Based Language Representation Models - Visualisierung von Aufmerksamkeit in transformerbasierten Sprachrepräsentationsmodellen
- A Survey of Long-Term Context in Transformers - Forschungstrends zur Verarbeitung langer Kontexte in Transformers
- Reformer: The Efficient Transformer - Reformer-Modell zur Verbesserung der Effizienz von Transformers
- Efficient Transformers: A Survey - Forschungstrends zu effizienten Transformer-Modellen
- Long Range Arena: A Benchmark for Efficient Transformers - Benchmark für die Verarbeitung langer Kontexte in Transformers