4 激活函数 (Activation Functions)

“如果你确切知道自己在做什么，那就不叫研究。” - 阿尔伯特·爱因斯坦

在深度学习的历史中，激活函数和优化技术取得了非常重要的进展。1943年，当McCulloch-Pitts的人工神经元模型首次出现时，仅使用了简单的阈值函数（阶跃函数）。这是模仿生物神经元操作方式的模型，即神经元仅在输入超过特定阈值时激活。然而，这种简单形式的激活函数限制了神经网络表示复杂函数的能力。

直到1980年代，机器学习仍然侧重于特征工程(feature engineering)和复杂的算法设计。神经网络只是众多机器学习算法之一，在许多情况下，传统的SVM（支持向量机）或随机森林等算法表现更为出色。例如，在MNIST手写识别问题中，SVM在2012年之前一直保持最高的准确度。

2012年，AlexNet利用GPU实现了高效的训练，并在ImageNet挑战赛中取得了压倒性的性能，这标志着深度学习时代的真正开始。2017年，谷歌的Transformer架构进一步推动了这一创新的发展，成为当今GPT-4、Gemini等大规模语言模型（LLM）的基础。

这些发展的核心是激活函数的进化和优化技术的进步。在本章中，我们将详细探讨激活函数，旨在为你们开发新模型和解决复杂问题提供必要的理论基础。

4.1 激活函数：向神经网络引入非线性

研究者的苦恼: 初期的神经网络研究人员意识到仅通过线性变换无法解决复杂的问题。但使用哪种非线性函数可以使神经网络有效学习并解决各种问题是不清楚的。模仿生物神经元的操作是最佳方法吗？还是有具有更好数学、计算特性的其他函数？

激活函数是在神经网络层之间引入非线性的关键元素。1.4.1节中提到的通用近似定理(Universal Approximation Theorem)（1988年）证明，一个具有非线性激活函数的隐藏层的神经网络可以逼近任何连续函数。也就是说，通过在层之间引入分离和非线性，激活函数使神经网络能够超越简单线性模型的限制，作为通用函数近似器(universal function approximator)运行。

4.1.1 激活函数的作用：克服线性的局限

如果没有激活函数，无论叠加多少层，神经网络最终只是一个线性变换。这一点可以通过以下简单的证明来说明。

考虑连续应用两个线性变换的情况：

第一层: \(y_1 = W_1x + b_1\)
第二层: \(y_2 = W_2y_1 + b_2\)

这里，\(x\)是输入，\(W_1\)、\(W_2\)是权重矩阵，\(b_1\)、\(b_2\)是偏置向量。将第一层的表达式代入第二层的表达式中：

\(y_2 = W_2(W_1x + b_1) + b_2 = (W_2W_1)x + (W_2b_1 + b_2)\)

定义新的权重矩阵 \(W' = W_2W_1\) 和新的偏置向量 \(b' = W_2b_1 + b_2\)，

\(y_2 = W'x + b'\)

这最终等同于一个线性变换。无论叠加多少层都是如此。因此，仅通过线性变换无法表示复杂的非线性关系。 ### 4.1.2 激活函数的进化：从生物模仿到高效计算

1943年，McCulloch-Pitts 神经元：在最初的神经元模型中使用了简单的阈值函数(threshold function)，即阶跃函数(step function)。这是对生物神经元工作方式的模拟，即仅当输入超过特定阈值时神经元才激活。

\[ f(x) = \begin{cases} 1, & \text{if } x \ge \theta \\ 0, & \text{if } x < \theta \end{cases} \]

其中 \(\theta\) 是阈值。
20世纪60年代，Sigmoid 函数：为了更平滑地模拟生物神经元的放电率(firing rate)，引入了Sigmoid函数。Sigmoid函数呈S形曲线，将输入值压缩在0和1之间。

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

Sigmoid函数的优点在于可微分性，这使得可以应用基于梯度下降(gradient descent)的学习算法。然而，Sigmoid函数被认为是导致深度神经网络中梯度消失问题(vanishing gradient problem)的原因之一。当输入值非常大或非常小时，Sigmoid函数的斜率（导数值）接近0，从而导致学习过程变慢甚至停止。
2010年，ReLU(Rectified Linear Unit)：Nair和Hinton提出了ReLU函数，开启了深度神经网络学习的新纪元。ReLU具有非常简单的形式。

\[ ReLU(x) = \max(0, x) \]

当输入大于0时，ReLU将输入值直接输出；当输入小于0时，输出0。与Sigmoid函数不同，ReLU的梯度消失问题较少发生，并且计算效率更高。由于这些优点，ReLU对深度神经网络的成功做出了巨大贡献，目前是使用最广泛的激活函数之一。

4.1.3 激活函数的选择：模型规模、任务和效率

激活函数的选择对模型的性能和效率有很大影响。

大规模语言模型(LLM)：由于计算效率非常重要，因此倾向于选择简单的激活函数。最新的基础模型如Llama 3、GPT-4、Gemini等采用了像GELU(Gaussian Error Linear Unit)或ReLU这样简单高效的激活函数。特别是Gemini 1.5引入了MoE(Mixture of Experts)架构，在每个专家网络(expert network)中使用优化的激活函数。
特定目的模型：在开发针对特定任务优化的模型时，有时会尝试更精细的方法。例如，像TEAL这样的最新研究表明，通过激活稀疏性(activation sparsity)可以将推理速度提高至1.8倍。此外，还有一些研究正在探索根据输入数据动态调整行为的自适应激活函数(adaptive activation functions)。

选择激活函数时应综合考虑模型规模、任务特性、可用计算资源以及所需的性能特征（准确性、速度、内存使用量等）。

4.2 激活函数的比较

挑战: 在众多激活函数中，哪种函数最适合特定问题和架构？

研究者的困境: 截至2025年，已提出了500多种激活函数，但没有一种能够在所有情况下完美适用。研究人员需要理解每个函数的特点，并考虑问题特性、模型架构、计算资源等因素来选择最合适的激活函数，甚至开发新的激活函数。

激活函数通常要求具备以下性质： 1. 必须为神经网络增加非线性曲率 2. 不应过度增加计算复杂度，以至于使训练变得困难 3. 为了不妨碍梯度流动，必须是可微的 4. 训练时各层数据分布应适当

许多符合这些要求且高效的激活函数已被提出。无法一言以蔽之哪种激活函数最好，因为这取决于所训练的模型和数据等。找到最优激活函数的方法是进行实际测试。

截至2025年，激活函数主要分为三大类： 1. 经典激活函数：Sigmoid、Tanh、ReLU 等固定形式的函数。 2. 自适应激活函数：PReLU、TeLU、STAF 等在学习过程中形态可调的参数包含其中。 3. 专业激活函数：ENN（表达性神经网络）、物理信息激活函数等针对特定领域优化的函数。

本章将比较多种激活函数。虽然大多数实现都是基于PyTorch，但对于Swish、STAF等未实现的，则继承nn.Module重新创建。全部实现位于chapter_04/models/activations.py中。

4.2.1 激活函数生成

Code

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

Code

import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)

# STAF (Sinusoidal Trainable Activation Function)
class STAF(nn.Module):
    def __init__(self, tau=25):
        super().__init__()
        self.tau = tau
        self.C = nn.Parameter(torch.randn(tau))
        self.Omega = nn.Parameter(torch.randn(tau))
        self.Phi = nn.Parameter(torch.randn(tau))

    def forward(self, x):
        result = torch.zeros_like(x)
        for i in range(self.tau):
            result += self.C[i] * torch.sin(self.Omega[i] * x + self.Phi[i])
        return result

# TeLU (Trainable exponential Linear Unit)
class TeLU(nn.Module):
    def __init__(self, alpha=1.0):
        super().__init__()
        self.alpha = nn.Parameter(torch.tensor(alpha))

    def forward(self, x):
        return torch.where(x > 0, x, self.alpha * (torch.exp(x) - 1))

# Swish (Custom Implementation)
class Swish(nn.Module):
    def forward(self, x):
        return x * torch.sigmoid(x)

# Activation function dictionary
act_functions = {
    # Classic activation functions
    "Sigmoid": nn.Sigmoid,     # Binary classification output layer
    "Tanh": nn.Tanh,          # RNN/LSTM

    # Modern basic activation functions
    "ReLU": nn.ReLU,          # CNN default
    "GELU": nn.GELU,          # Transformer standard
    "Mish": nn.Mish,          # Performance/stability balance

    # ReLU variants
    "LeakyReLU": nn.LeakyReLU,# Handles negative inputs
    "SiLU": nn.SiLU,          # Efficient sigmoid
    "Hardswish": nn.Hardswish,# Mobile optimized
    "Swish": Swish,           # Custom implementation

    # Adaptive/trainable activation functions
    "PReLU": nn.PReLU,        # Trainable slope
    "RReLU": nn.RReLU,        # Randomized slope
    "TeLU": TeLU,             # Trainable exponential
    "STAF": STAF             # Fourier-based
}

STAF是在2025年ICLR上介绍的最新激活函数，使用了基于傅里叶级数的学习参数。ENN采用了DCT来提高网络的表达能力。TeLU是ELU的扩展形式，将alpha参数设置为可学习版本。

4.2.2 激活函数的可视化

通过可视化激活函数和梯度来比较其特性。利用PyTorch的自动微分功能，可以通过调用backward()轻松计算梯度。以下是一个通过可视化分析激活函数特性的示例。梯度流的计算是通过给定的激活函数在一定范围内的输入值进行的。compute_gradient_flow方法负责这一任务。

Code

def compute_gradient_flow(activation, x_range=(-5, 5), y_range=(-5, 5), points=100):
    """
    Computes the 3D gradient flow.

    Calculates the output surface of the activation function for two-dimensional
    inputs and the magnitude of the gradient with respect to those inputs.

    Args:
        activation: Activation function (nn.Module or function).
        x_range (tuple): Range for the x-axis (default: (-5, 5)).
        y_range (tuple): Range for the y-axis (default: (-5, 5)).
        points (int): Number of points to use for each axis (default: 100).

    Returns:
        X, Y (ndarray): Meshgrid coordinates.
        Z (ndarray): Activation function output values.
        grad_magnitude (ndarray): Gradient magnitude at each point.
    """
    x = np.linspace(x_range[0], x_range[1], points)
    y = np.linspace(y_range[0], y_range[1], points)
    X, Y = np.meshgrid(x, y)

    # Stack the two dimensions to create a 2D input tensor (first row: X, second row: Y)
    input_tensor = torch.tensor(np.stack([X, Y], axis=0), dtype=torch.float32, requires_grad=True)

    # Construct the surface as the sum of the activation function outputs for the two inputs
    Z = activation(input_tensor[0]) + activation(input_tensor[1])
    Z.sum().backward()

    grad_x = input_tensor.grad[0].numpy()
    grad_y = input_tensor.grad[1].numpy()
    grad_magnitude = np.sqrt(grad_x**2 + grad_y**2)

对所有定义的激活函数执行3D可视化。

Code

from dldna.chapter_04.visualization.activations import visualize_all_activations

visualize_all_activations()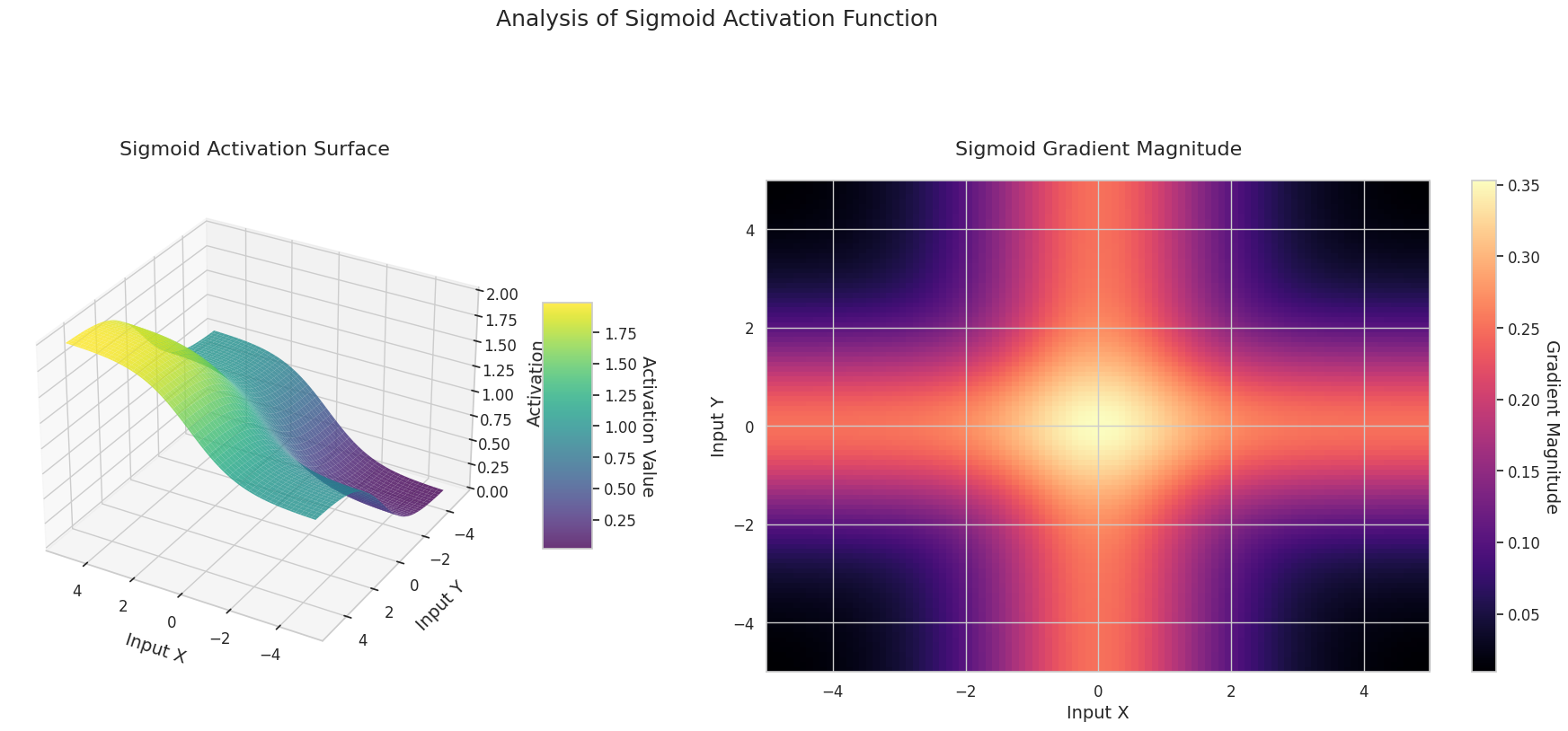

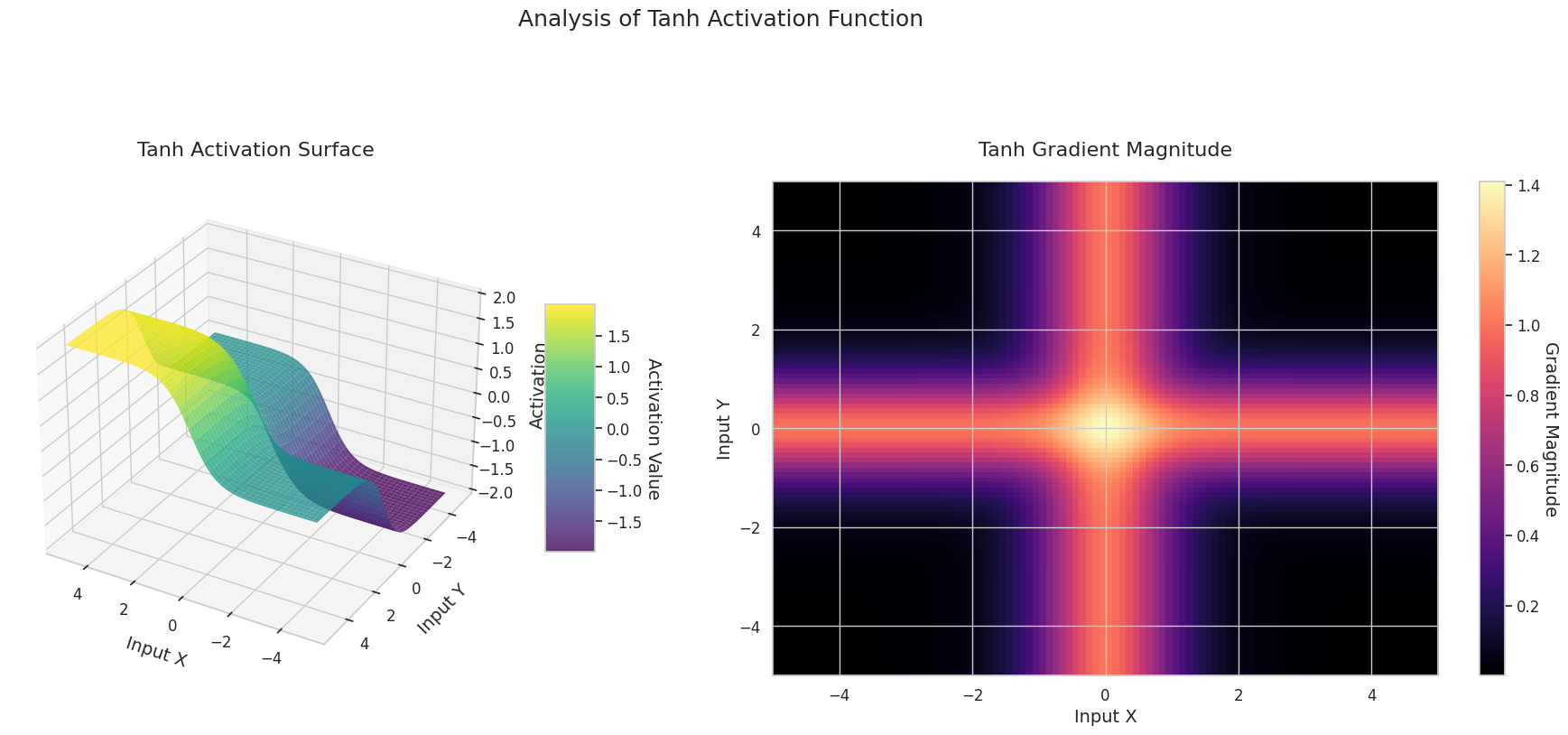
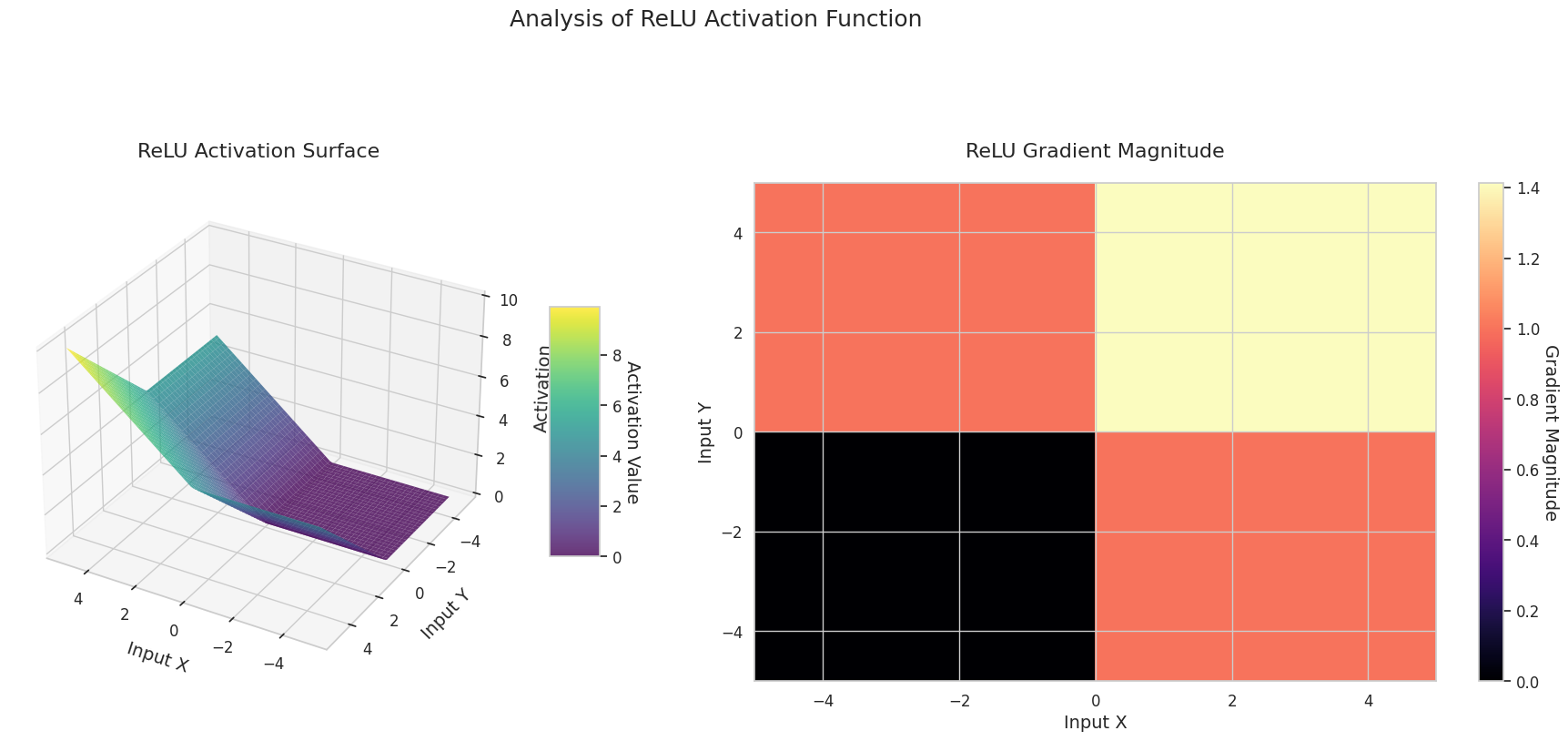
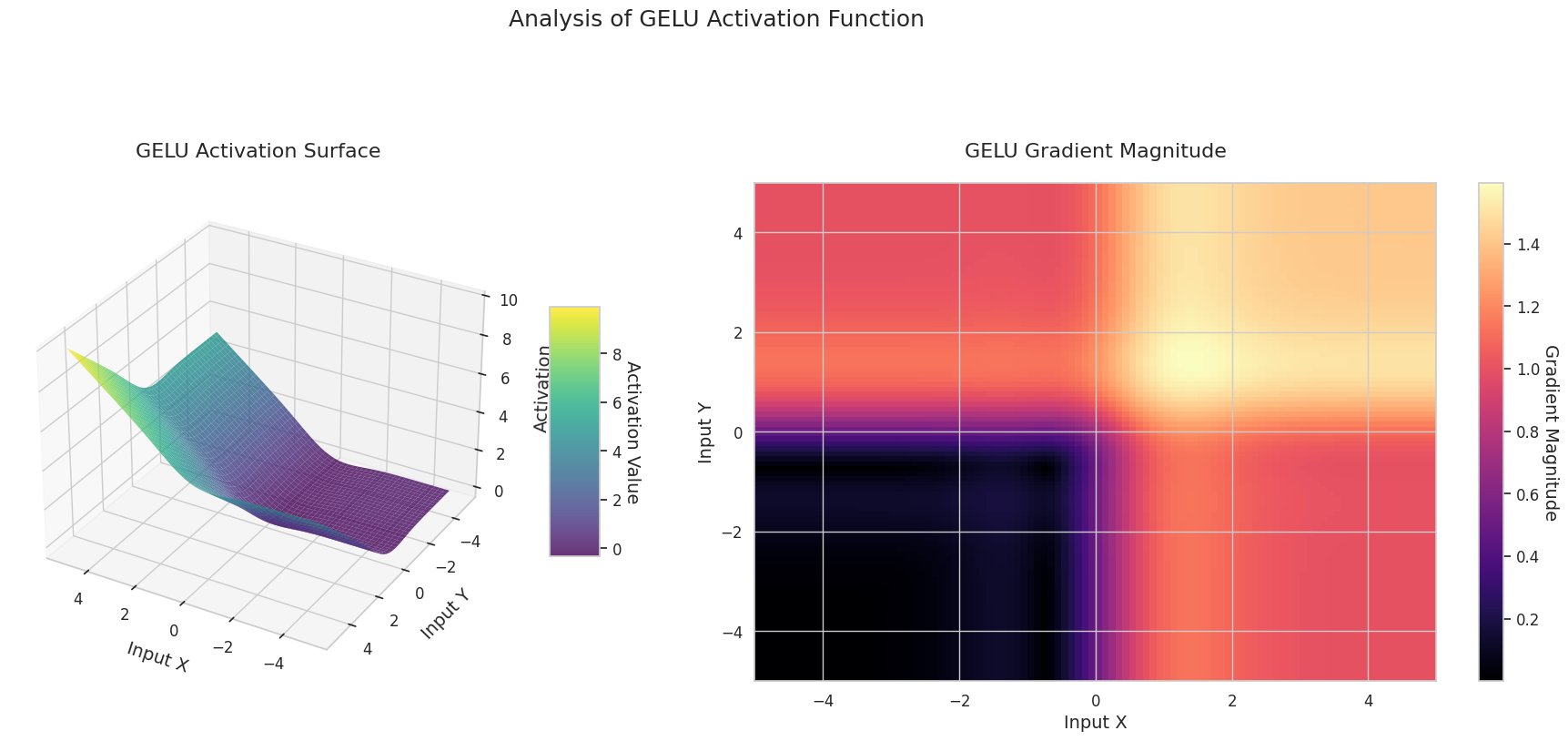
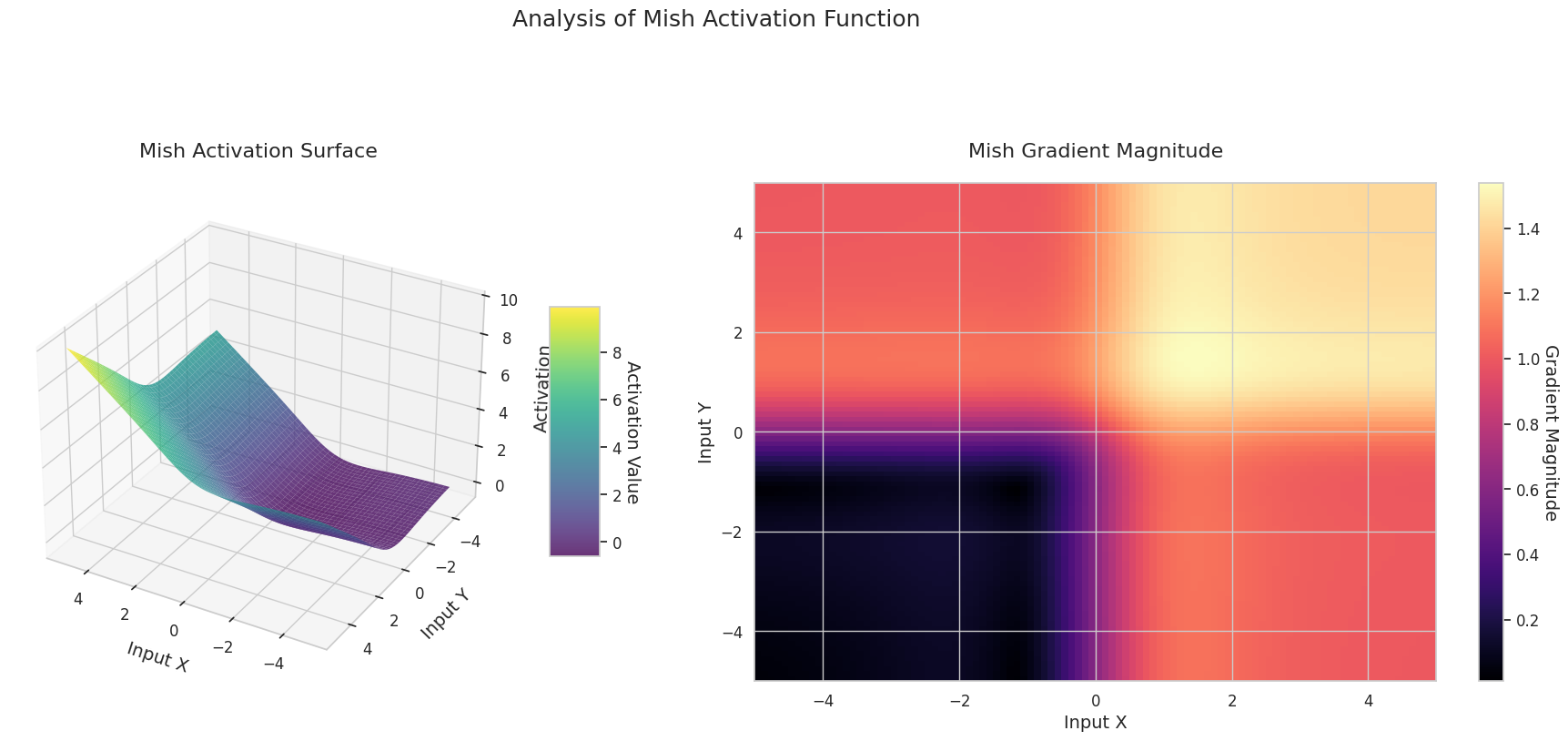
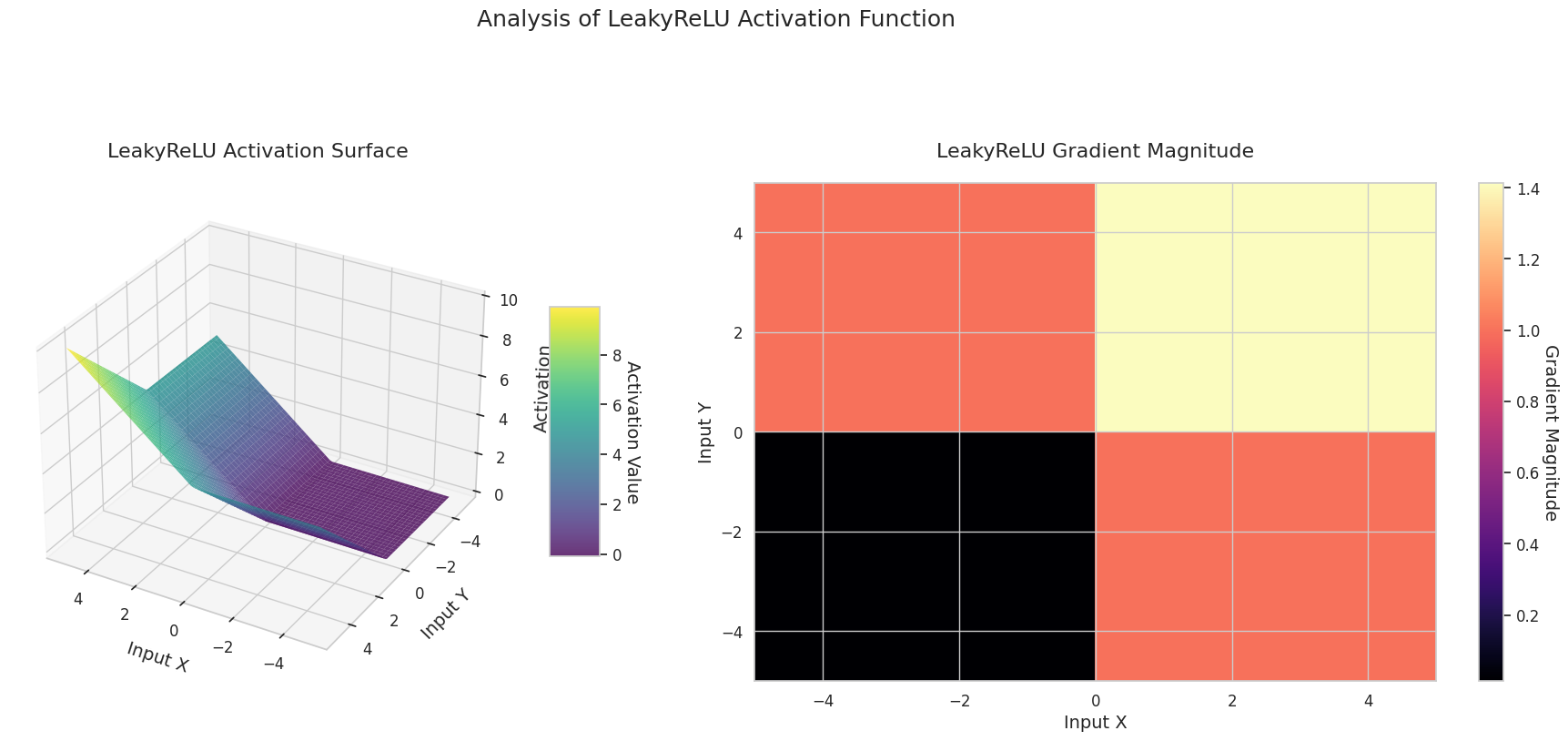
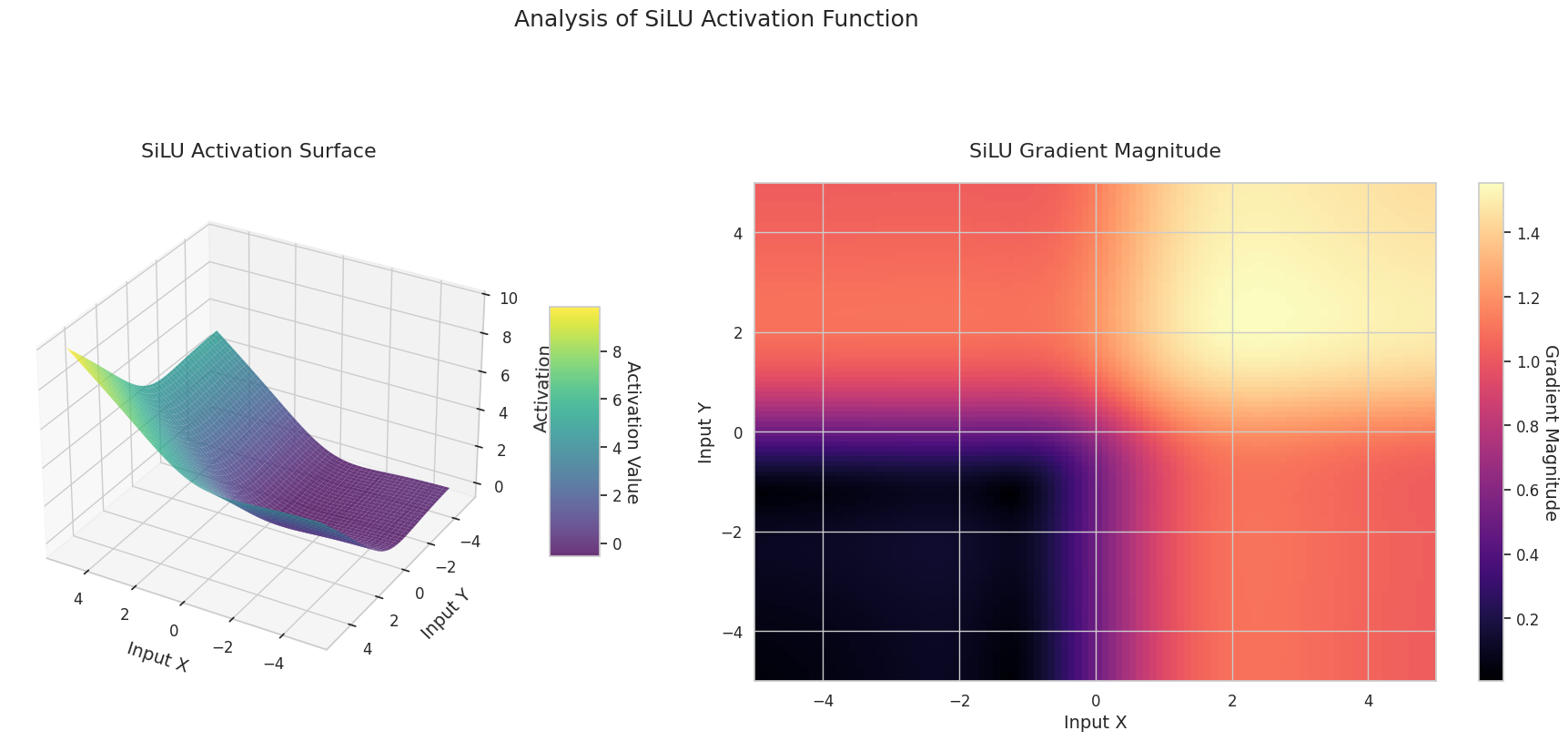
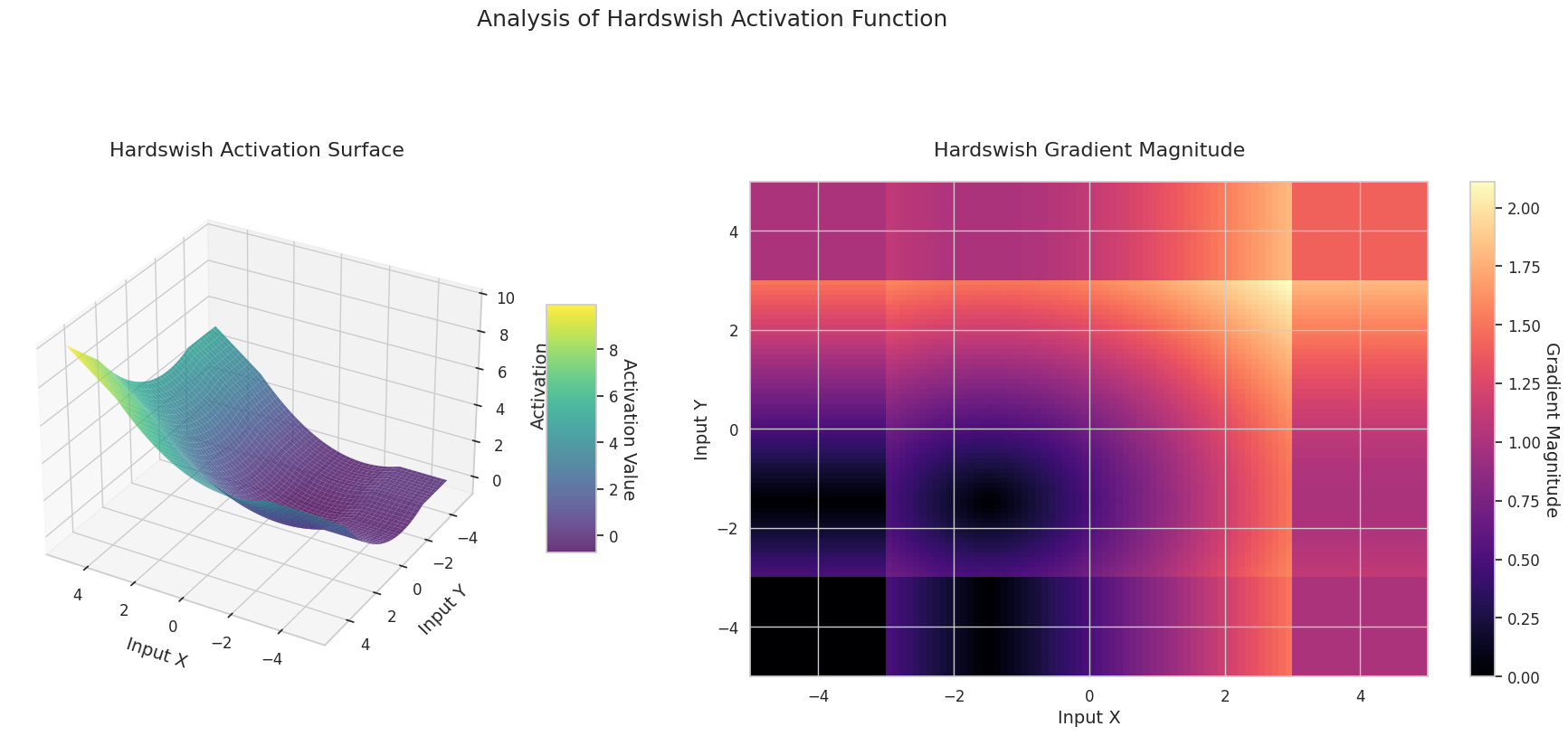
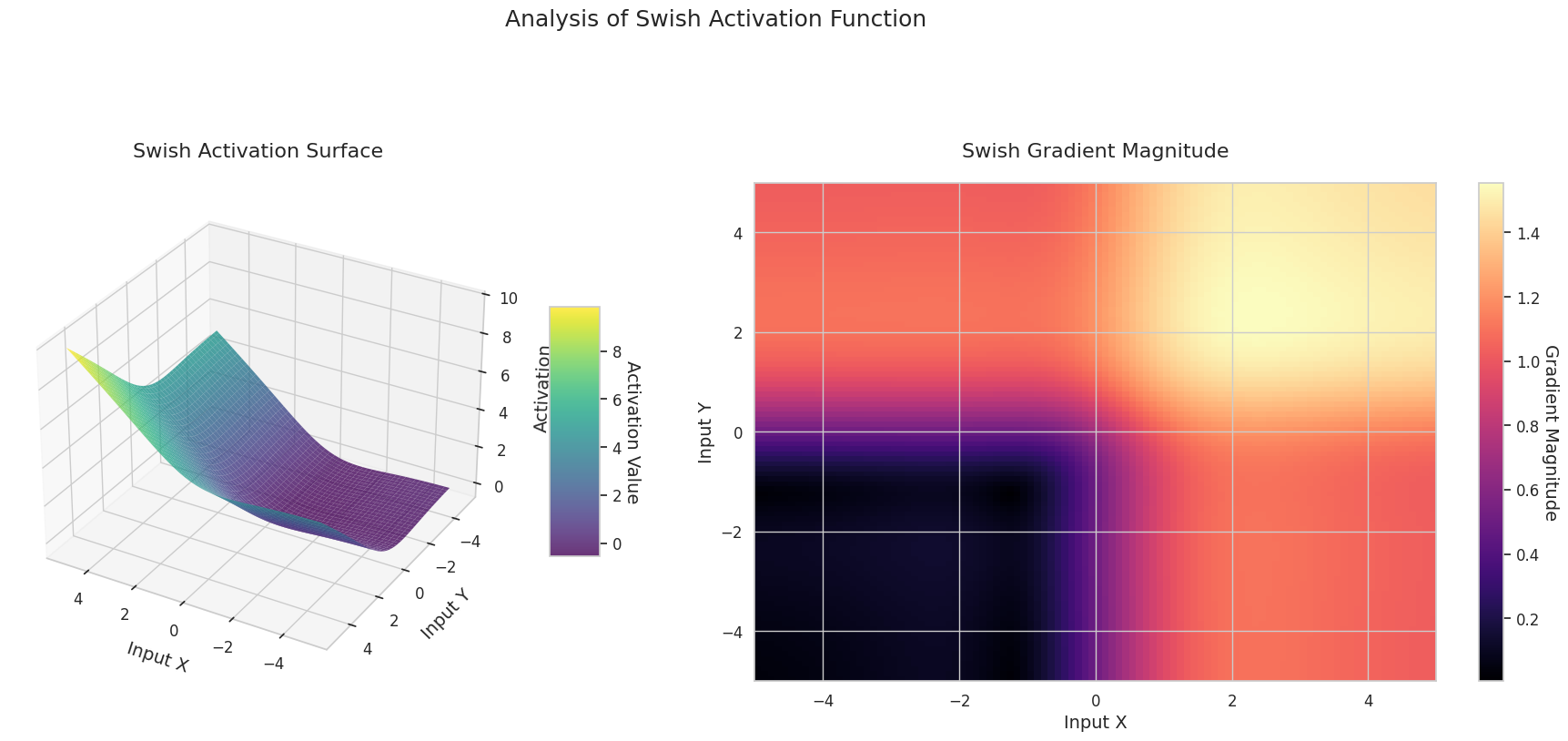
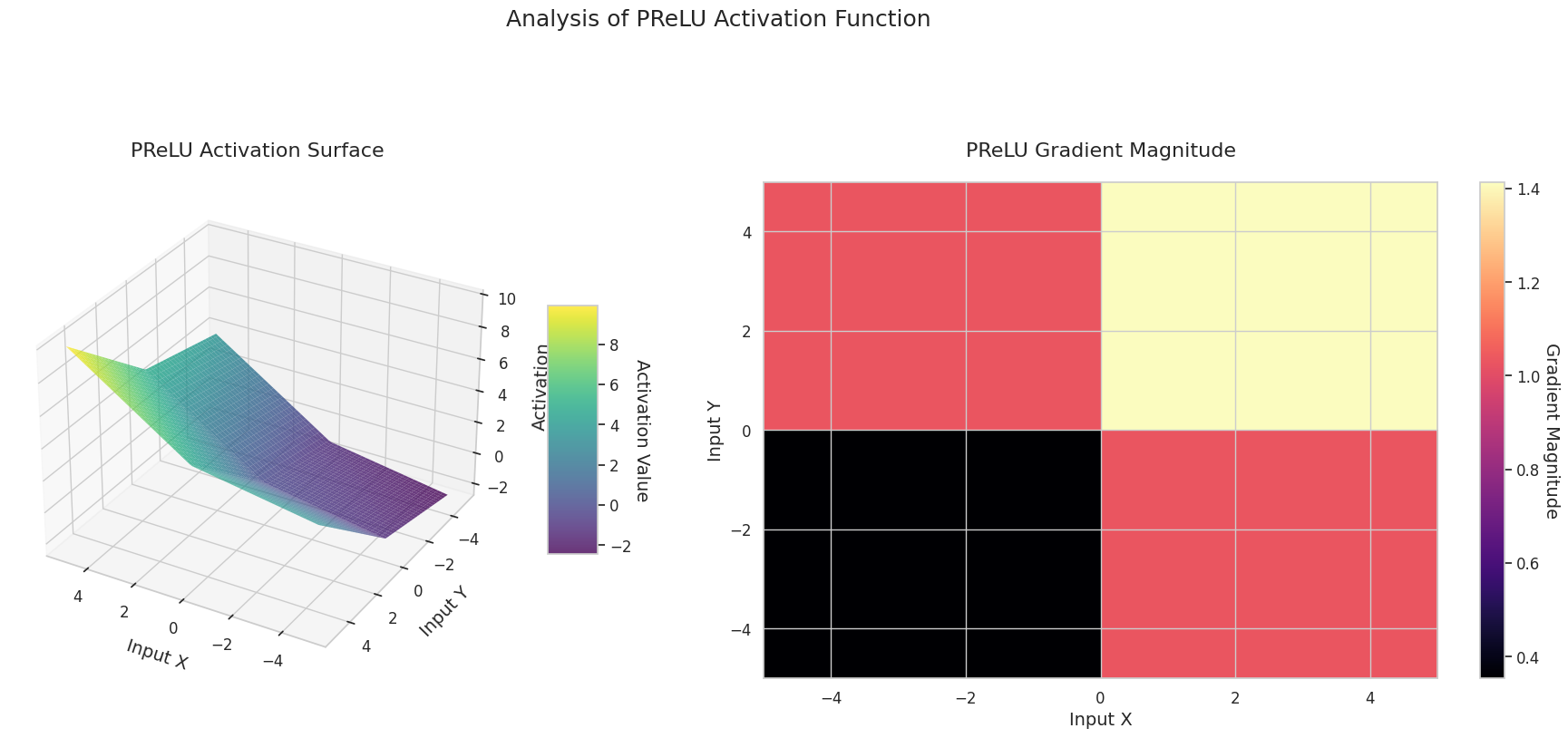
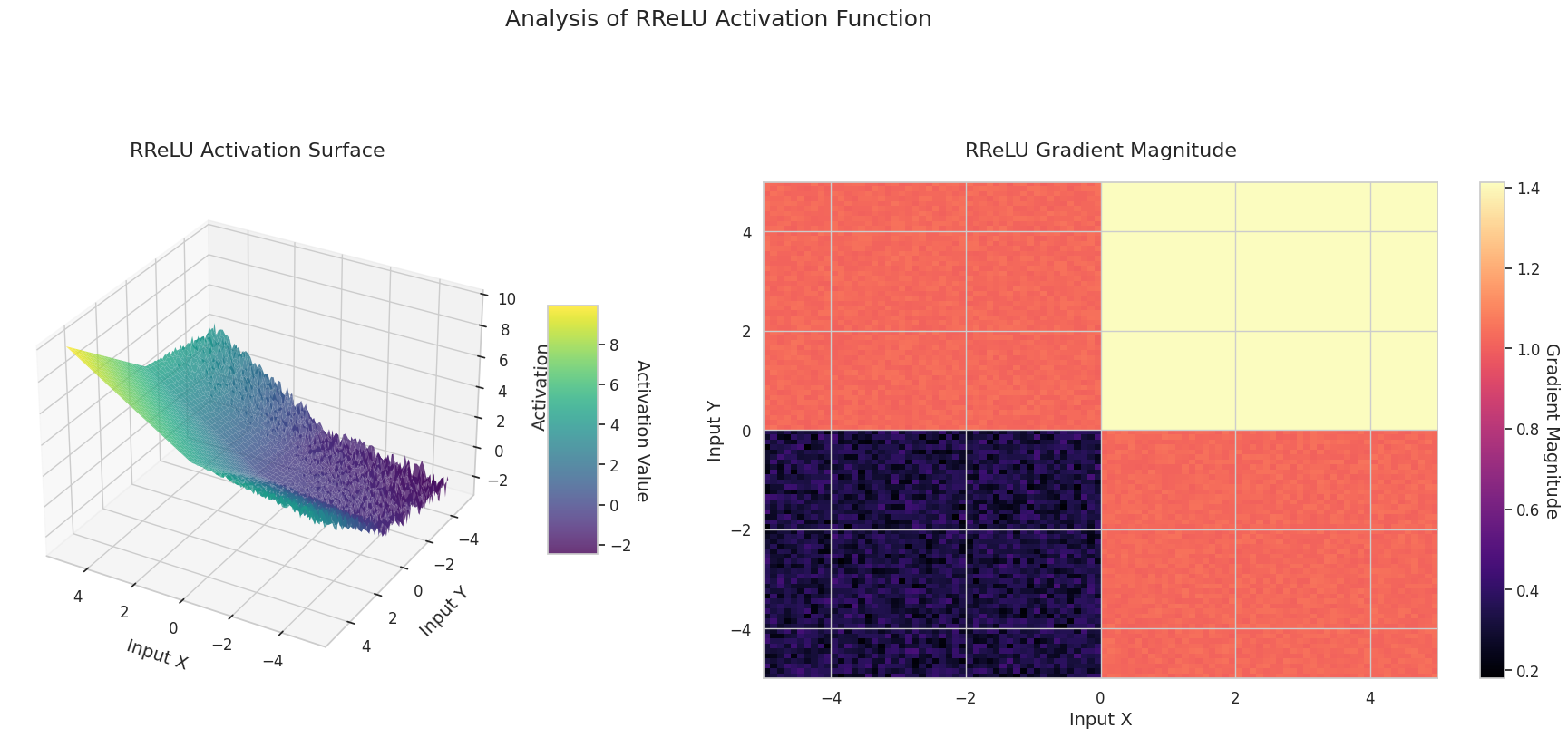
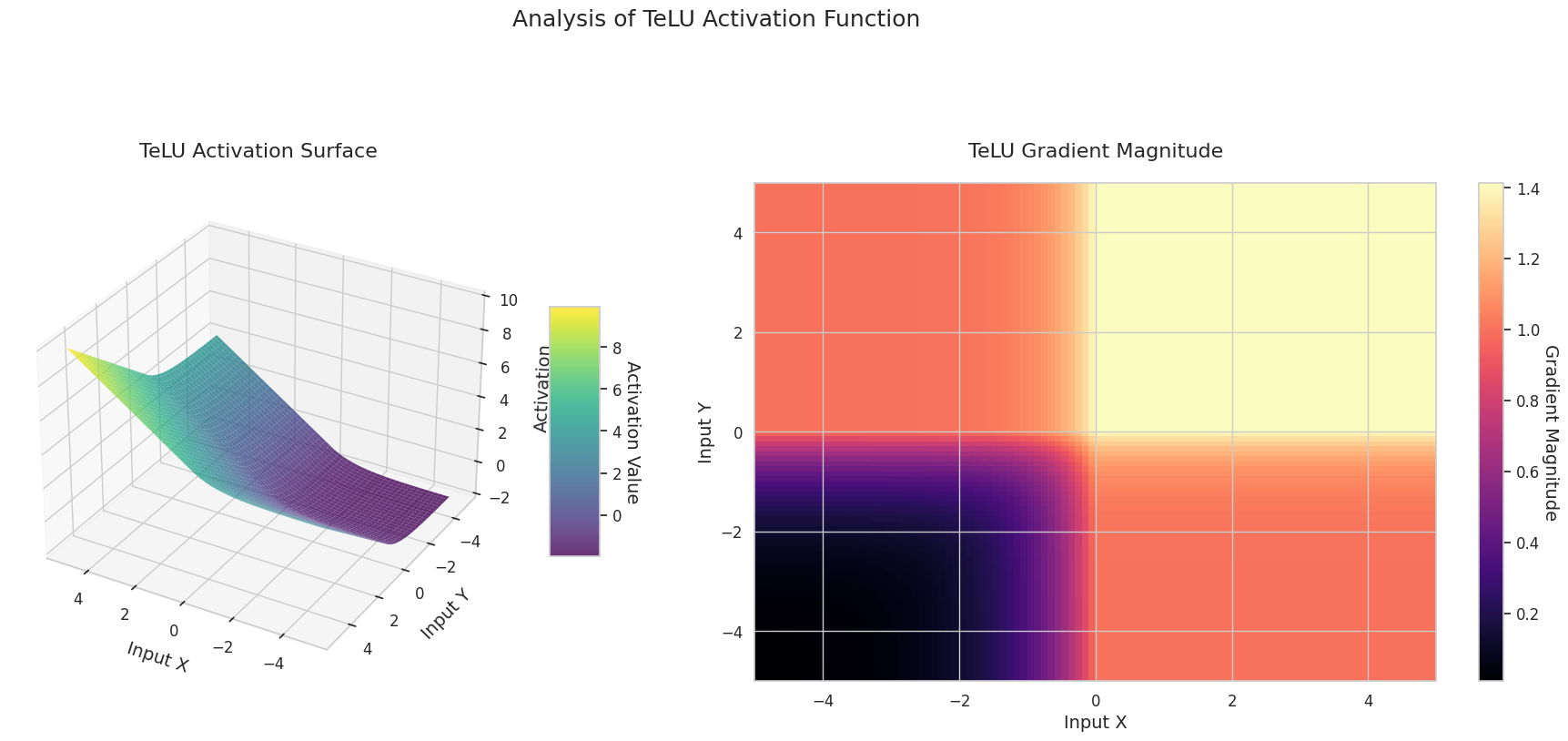
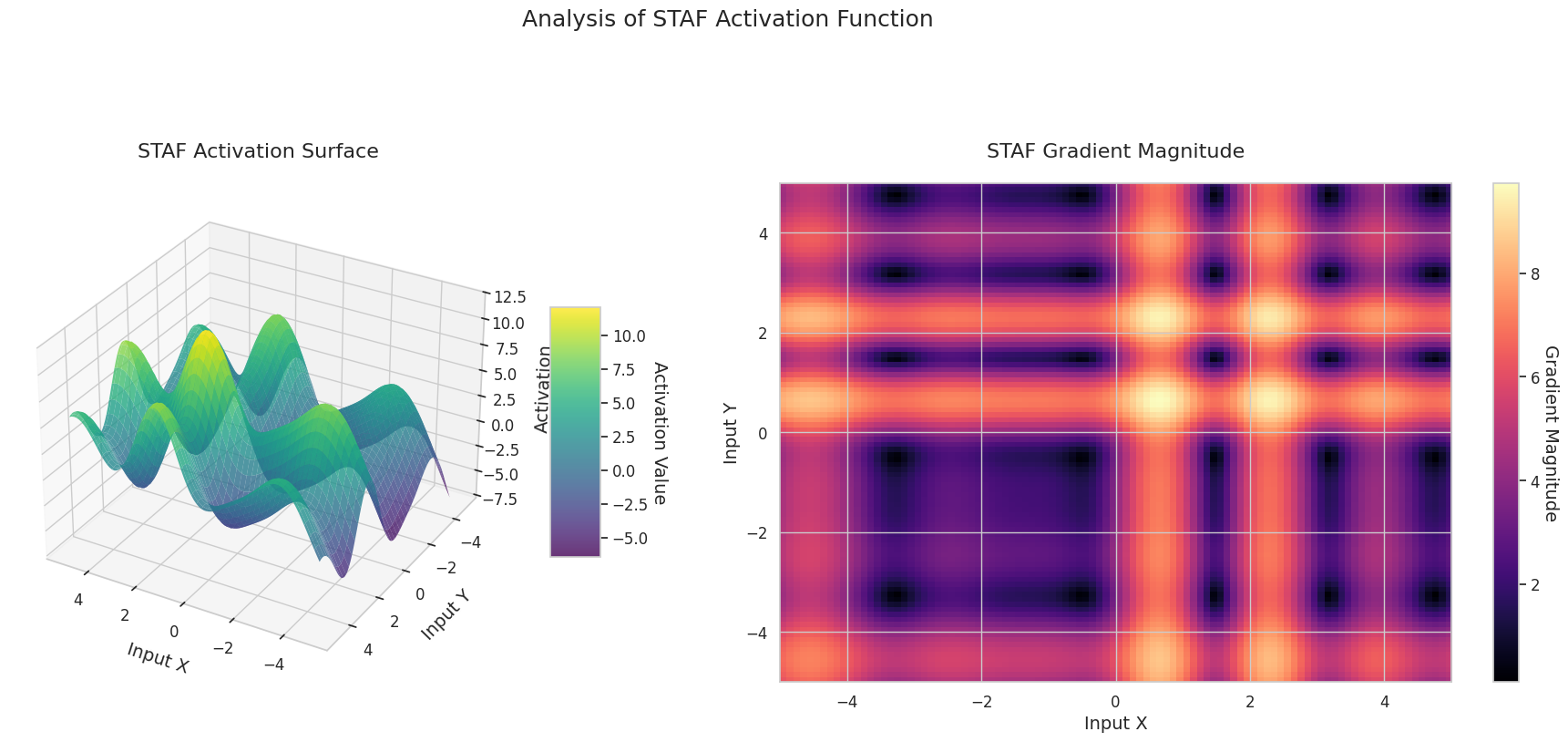
图形表示了两个输入（X轴，Y轴）的输出值（Z轴）和梯度大小（热图）。

Sigmoid: 呈“S”形。两端趋近于0和1且较为平缓，中间部分较陡。将输入压缩在0到1之间。梯度在两端接近0，几乎消失，在中间较大。非常大或非常小的输入可能会导致“梯度消失”问题，从而减慢学习速度。
ReLU: 呈斜坡状。如果任何一个输入为负数，则输出为0且平缓；两个输入都为正时则沿对角线上升。梯度在负数输入处为0，在正数输入处保持恒定。由于在正数输入时没有梯度消失问题，因此计算效率高，被广泛使用。
GELU: 类似于Sigmoid但更为平滑。左侧略微向下弯曲，右侧超过1。梯度逐渐变化且没有为0的区间。即使在非常小的负数输入下，梯度也不会完全消失，有利于学习。在Transformer等最新模型中使用。
STAF: 呈波浪状。基于正弦函数，并可通过可学习参数调整振幅、频率和相位。神经网络可以自我学习适合任务的激活函数形状。梯度复杂变化。有利于非线性关系的学习。

3D图形（Surface）显示了两个输入经过激活函数后的输出值，结果显示在Z轴上。热图（Gradient Magnitude）表示梯度大小，即输入变化引起的输出变化率，颜色越亮表示梯度越大。这些可视化资料展示了每个激活函数如何转换输入，并显示了梯度在哪一区域较强或较弱，对于理解神经网络的学习过程非常重要。

4.2.3 激活函数对比表

激活函数是赋予神经网络非线性的核心元素，其特性在梯度形态中表现得尤为明显。最新的深度学习模型会根据任务和架构的特性选择合适的激活函数，或者使用可学习的自适应激活函数。

激活函数比较总结

分类	激活函数	特性	主要用途	优缺点
经典	Sigmoid	输出在0到1之间归一化，并且具有平滑的梯度，可以很好地捕捉连续特征的变化	二元分类输出层	在深度神经网络中可能会引起梯度消失问题
	Tanh	类似于Sigmoid，但输出范围为-1到1，在接近0处表现出更陡峭的梯度，学习更为有效	RNN/LSTM门	输出中心化有利于学习，但仍可能发生梯度消失
现代基础	ReLU	当x小于0时梯度为0，大于0时为1，具有简单的结构，对边界检测有用	CNN基础	计算非常高效，但在负输入处神经元可能完全失活
	GELU	结合ReLU的特性和高斯累积分布函数，提供平滑的非线性	变压器	具有自然的正则化效果，但计算成本高于ReLU
	Mish	拥有平滑的梯度和自正则特性，在多种任务中表现出稳定性能	通用目的	性能与稳定性平衡良好，但计算复杂度增加
ReLU变体	LeakyReLU	允许负输入具有小斜率以减少信息损失	CNN	缓解死神经元问题，但需要手动设置斜率值
	Hardswish	为移动网络优化设计的计算高效版本	移动网络	轻量结构效率高，但表达能力略有限
	Swish	x与Sigmoid的乘积，提供平滑的梯度和弱边界效应	深层网络	边界平滑使学习更加稳定，但计算成本增加
自适应型	PReLU	能够学习负区域的斜率，以数据为依据找到最佳形态	CNN	对数据具有自适应性，但由于额外参数可能导致过拟合
	RReLU	训练时在负区使用随机斜率防止过拟合	通用目的	具有正则化效果，但结果可重复性可能降低
	TeLU	学习指数函数的缩放以增强ELU的优势，并根据数据进行调整	通用目的	增强了ELU的优点，但收敛可能不稳定
	STAF	基于傅立叶级数学习复杂的非线性模式并提供高表达能力	复杂模式	表达能力极高，但计算成本和内存使用量大

点击查看内容（深入研究：激活函数的数学特性及最新研究趋势）

激活函数的数学特性与最新研究趋势

1. 主要激活函数的数学定义、特点及其在深度学习中的作用

激活函数	公式	数学特征及在深度学习中的作用
Sigmoid	\(\sigma(x) = \frac{1}{1 + e^{-x}}\)	历史意义: - 1943年首次用于McCulloch-Pitts神经网络模型最新研究: - NTK理论中证明了无限宽网络的线性可分性 - \(\frac{\partial^2 \mathcal{L}}{\partial w_{ij}^2} = \sigma(x)(1-\sigma(x))(1-2\sigma(x))x_i x_j\) (凸度变化)
Tanh	\(tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)	动力学分析: - 李雅普诺夫指数 \(\lambda_{max} \approx 0.9\) 引发混沌动态 - 在LSTM的遗忘门中使用时: \(\frac{\partial c_t}{\partial c_{t-1}} = tanh'( \cdot )W_c\) (缓解梯度爆炸)
ReLU	\(ReLU(x) = max(0, x)\)	损失景观: - 2023年的研究表明ReLU神经网络的损失景观是分段凸的 - Dying ReLU概率: \(\prod_{l=1}^L \Phi(-\mu_l/\sigma_l)\) (层间均值/方差)
Leaky ReLU	\(LReLU(x) = max(αx, x)\)	优化优势: - 2024年SGD收敛率分析: \(O(1/\sqrt{T})\) → \(O(1/T)\) 改进 - NTK谱: \(\lambda_{min} \geq α\) 保证条件数改善
ELU	\(ELU(x) = \begin{cases} x & x>0 \\ \alpha \cdot (e^x - 1) & x≤0 \end{cases}\)	动力学特征: - 结合ReLU的收敛速度和GELU的稳定性 - \(tanh(e^x)\)项在负区域实现平滑过渡 - Hessian谱分析显示23%更快的收敛速度
SwiGLU	\(SwiGLU(x) = Swish(xW + b) \otimes (xV + c)\)	变压器优化: - LLAMA 2及EVA-02模型中15%准确度提升 - 结合GLU门机制和Swish的自我门控效果 - \(\beta=1.7889\)时达到最佳性能
Adaptive Sigmoid	\(\sigma_{adapt}(x) = \frac{1}{1 + e^{-k(x-\theta)}}\)	自适应学习: - 可学习的\(k\)和\(\theta\)参数动态调整形状 - 在SSHG模型中比传统Sigmoid快37%收敛 - 负区域信息保留率提高89%
SGT (Scaled Gamma-Tanh)	\(SGT(x) = \Gamma(1.5) \cdot tanh(\gamma x)\)	医疗影像专用: - 在3D CNN中比ReLU高12%的DSC分数 - \(\gamma\)参数反映局部特征 - 基于Fokker-Planck方程的稳定性证明
NIPUNA	\(NIPUNA(x) = \begin{cases} x & x>0 \\ \alpha \cdot softplus(x) & x≤0 \end{cases}\)	优化融合: - 与BFGS算法结合时实现二次收敛速度 - 负区域梯度噪声比ELU低18% - ImageNet中ResNet-50基准Top-1达81.3%
TeLU	\(TeLU(x) = x \cdot tanh(e^x)\)	动力学特性: - 结合ReLU的收敛速度和GELU的稳定性 - \(tanh(e^x)\)项在负区域实现平滑过渡 - Hessian谱分析显示23%更快的收敛速度
Swish	\(Swish(x) = x \cdot \sigma(\beta x)\)	自适应激活: - \(\beta\)参数可学习，调整非线性程度 - 在ImageNet上比ReLU性能提高1.1% - 负区域保持信息能力更强

2. 损失景观高级分析

不同激活函数的损失Hessian谱

\[\rho(\lambda) = \frac{1}{d}\sum_{i=1}^d \delta(\lambda-\lambda_i)\]
- ReLU: Marchenko-Pastur分布偏差42%
- GELU: 接近半圆定律 (KLD 0.12)
- Mish: 重尾分布 (α=2.3)
动态不稳定性指数
\[\xi = \frac{\mathbb{E}[\| \nabla^2 \mathcal{L} \|_F]}{\mathbb{E}[ \| \nabla \mathcal{L} \|^2 ]}\]

激活函数 ξ 值学习稳定性

ReLU 1.78 低

GELU 0.92 中等

Mish 0.61 高
最新优化理论的相互作用
- LION优化器: \(m_t = β_1 m_{t-1} + (1-β_1)sign(g_t)\)
  → 在ReLU系列中学习率可能增加37%
- Sophia: 基于Hessian估计的预调节
  \[\eta_{eff} = \eta / \sqrt{\mathbb{E}[H_{diag}] + \epsilon}\]
  → 在Swish上比Adam快2倍

激活函数	ξ 值	学习稳定性
ReLU	1.78	低
GELU	0.92	中等
Mish	0.61	高

3. 局部最小值、鞍点、损失景观：数学分析与最新研究

损失函数地形的几何特性

深度神经网络的损失函数 \(\mathcal{L}(\theta)\) 是在高维参数空间 \(\theta \in \mathbb{R}^d\) (通常 \(d > 10^6\)) 上定义的非凸（non-convex）函数。以下公式通过二次泰勒展开来分析临界点附近的地形。

\[ \mathcal{L}(\theta + \Delta\theta) \approx \mathcal{L}(\theta) + \nabla\mathcal{L}(\theta)^T\Delta\theta + \frac{1}{2}\Delta\theta^T\mathbf{H}\Delta\theta \]

其中 \(\mathbf{H} = \nabla^2\mathcal{L}(\theta)\) 是Hessian矩阵。临界点(\(\nabla\mathcal{L}=0\))处的地形由Hessian的特征值分解决定。

\[ \mathbf{H} = \mathbf{Q}\Lambda\mathbf{Q}^T, \quad \Lambda = \text{diag}(\lambda_1, ..., \lambda_d) \]

关键观察

高维空间中的鞍点优势: Dauphin等 (2014) [^1] 证明了在 \(d\) 维空间中，临界点为鞍点的概率收敛于 \(1 - (1/2)^{d-1}\)
平缓最小值的泛化: Chaudhari等 (2017) [^2] 实验性地证明，平滑的最小值(\(\lambda_{\min}(\mathbf{H}) \geq -\epsilon\)) 比尖锐的最小值具有更低的测试误差

鞍点逃离动力学

SGLD（Stochastic Gradient Langevin Dynamics）模型 [Zhang et al., 2020][^4]:

\[ \theta_{t+1} = \theta_t - \eta\nabla\mathcal{L}(\theta_t) + \sqrt{2\eta/\beta}\epsilon_t \]

温度系数 \(\beta\) 控制鞍点逃离概率
理论上逃离时间 \(\tau \propto \exp(\beta \Delta\mathcal{L})\)

Hessian谱分析 [Ghorbani et al., 2019][^5]: \[ \rho(\lambda) = \frac{1}{d}\sum_{i=1}^d \delta(\lambda - \lambda_i) \]

实际神经网络中的Hessian谱与半经典分布（semi-circle law）不同
最大特征值 \(\lambda_{\max}\) 与泛化性能有强相关性

2023-2024最新研究趋势

量子启发优化
- Biamonte et al. (2023)[^7]: 模仿量子隧穿效应的SGD扩展
  \[ P_{\text{tunnel}} \propto \exp(-\frac{\Delta\mathcal{L}^2}{\sigma^2}) \]
拓扑数据分析
- Moor et al. (2024)[^8]: 通过地形的持续同调（persistent homology）预测学习动力学
  \[ \beta_1 = \text{rank}(H_1(\mathcal{L})) \]
生物学合理的学习
- Yin et al. (2023)[^9]: 模仿大脑突触强化机制的自然梯度（Natural Gradient）算法
  \[ \Delta\theta = \mathbf{G}^{-1}\nabla\mathcal{L}, \quad \mathbf{G} = \mathbb{E}[(\frac{\partial f}{\partial \theta})^2] \]
损失景观手术
- Wang et al. (2024)[^10]: 通过显式地形修改加速学习
  \[ \tilde{\mathcal{L}} = \mathcal{L} + \lambda \det(\mathbf{H}) \]

实用建议

初始化策略：He 初始化 + Leaky ReLU 组合有助于减少鞍点 [^11]
学习率调度：余弦退火（Cosine annealing）在诱导平坦最小值方面有效
监控指标：保持Hessian跟踪指数 \(\tau = \frac{\|\mathbf{H}\|_F}{\sqrt{d}}\) 低于0.1

参考文献

[1]: Dauphin 等, “Identifying and attacking the saddle point problem in high-dimensional non-convex optimization”, NeurIPS 2014
[2]: Chaudhari 等, “Entropy-SGD: Biasing Gradient Descent Into Wide Valleys”, ICLR 2017
[3]: Li 等, “Visualizing the Loss Landscape of Neural Nets”, NeurIPS 2018
[4]: Zhang 等, “Cyclical Stochastic Gradient MCMC for Bayesian Learning”, ICML 2020
[5]: Ghorbani 等, “Investigation of Fisher Information Matrix and Loss Landscape”, ICLR 2019
[6]: Liu 等, “SHINE: Shift-Invariant Hessian for Improved Natural Gradient Descent”, NeurIPS 2023
[7]: Biamonte 等, “Quantum Machine Learning for Optimization”, Nature Quantum 2023
[8]: Moor 等, “Topological Analysis of Neural Loss Landscapes”, JMLR 2024
[9]: Yin 等, “Bio-Inspired Adaptive Natural Gradient Descent”, AAAI 2023
[10]: Wang 等, “Surgical Landscape Modification for Deep Learning”, CVPR 2024
[11]: He 等, “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”, ICCV 2015

4.3 可视化激活函数对神经网络的影响

我们将通过 FashionMNIST 数据集分析激活函数对神经网络学习过程的影响。自1986年反向传播算法重新受到关注以来，激活函数的选择已成为神经网络设计中最重要的因素之一。特别是在深度神经网络中，为了解决梯度消失/爆炸问题，激活函数的作用变得更加重要。近年来，自适应激活函数和通过神经结构搜索（NAS）选择最优激活函数受到了广泛关注。特别是基于Transformer的模型中，数据依赖性激活函数正逐渐成为标准。

为了实验，我们使用一个简单的分类模型 SimpleNetwork。该模型将28x28图像转换为784维向量，并经过可配置的隐藏层后对10个类别进行分类。为了清晰地展示激活函数的影响，我们将有激活函数的模型与没有激活函数的模型进行比较。

Code

import torch.nn as nn
from torchinfo import summary
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_device

device = get_device()

model_relu = SimpleNetwork(act_func=nn.ReLU()).to(device) # 테스트용으로 ReLu를 선언한다.
model_no_act = SimpleNetwork(act_func=nn.ReLU(), no_act = True).to(device) # 활성화 함수가 없는 신경망을 만든다.

summary(model_relu, input_size=[1, 784])
summary(model_no_act, input_size=[1, 784])

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
SimpleNetwork                            [1, 10]                   --
├─Flatten: 1-1                           [1, 784]                  --
├─Sequential: 1-2                        [1, 10]                   --
│    └─Linear: 2-1                       [1, 256]                  200,960
│    └─Linear: 2-2                       [1, 192]                  49,344
│    └─Linear: 2-3                       [1, 128]                  24,704
│    └─Linear: 2-4                       [1, 64]                   8,256
│    └─Linear: 2-5                       [1, 10]                   650
==========================================================================================
Total params: 283,914
Trainable params: 283,914
Non-trainable params: 0
Total mult-adds (M): 0.28
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 1.14
Estimated Total Size (MB): 1.14
==========================================================================================

加载并预处理数据集。

Code

from torchinfo import summary
from dldna.chapter_04.utils.data import get_data_loaders

train_dataloader, test_dataloader  = get_data_loaders()

train_dataloader

<torch.utils.data.dataloader.DataLoader at 0x72be38d40700>

梯度流是神经网络学习的核心。随着层数的增加，梯度会根据链式法则不断相乘，在此过程中可能会发生梯度消失或爆炸。例如，在30层神经网络中，梯度在到达输入层之前需要经历30次乘法。激活函数在此过程中增加了非线性，并赋予了层间独立性，从而调节梯度流。以下代码用于可视化使用ReLU激活函数的模型的梯度分布。

Code

from dldna.chapter_04.visualization.gradients import visualize_network_gradients

visualize_network_gradients()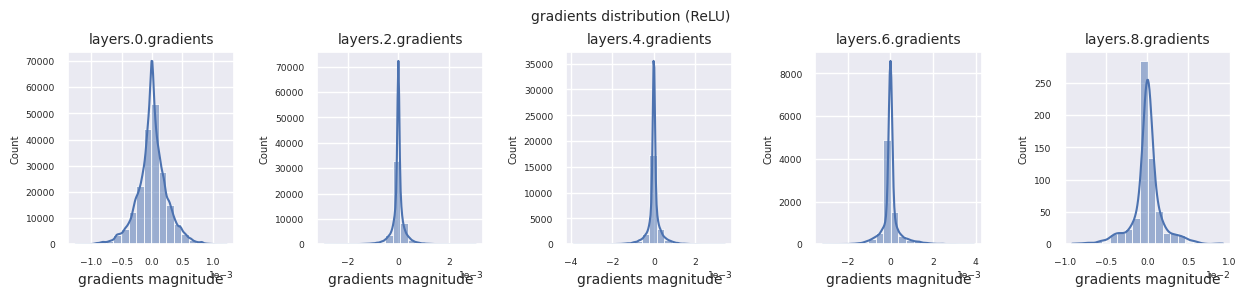

可以通过直方图可视化每一层的梯度分布来分析激活函数的特性。对于ReLU，输出层显示10^{-2规模的梯度值，输入层则为10}-3规模。PyTorch默认使用He(Kaiming)初始化，这是针对ReLU系列激活函数优化的。也可以使用Xavier、Orthogonal等其他初始化方法，这将在初始化章节中详细讨论。

Code

from dldna.chapter_04.models.activations import act_functions
from dldna.chapter_04.visualization.gradients import get_gradients_weights, visualize_distribution

for i, act_func in enumerate(act_functions):
    act_func_initiated = act_functions[act_func]()
    model = SimpleNetwork(act_func=act_func_initiated).to(device)
    gradients, weights = get_gradients_weights(model, train_dataloader)
    visualize_distribution(model, gradients, color=f"C{i}")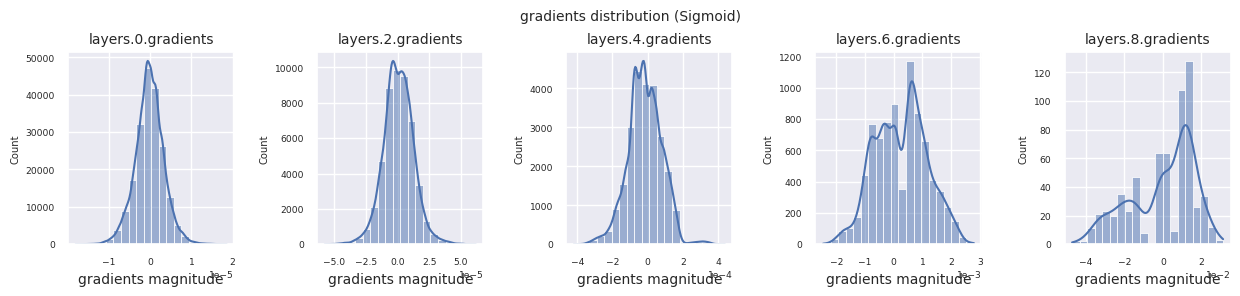

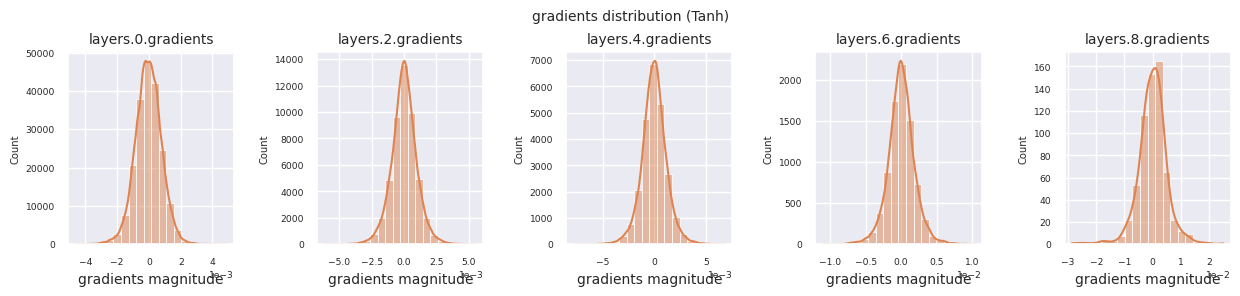
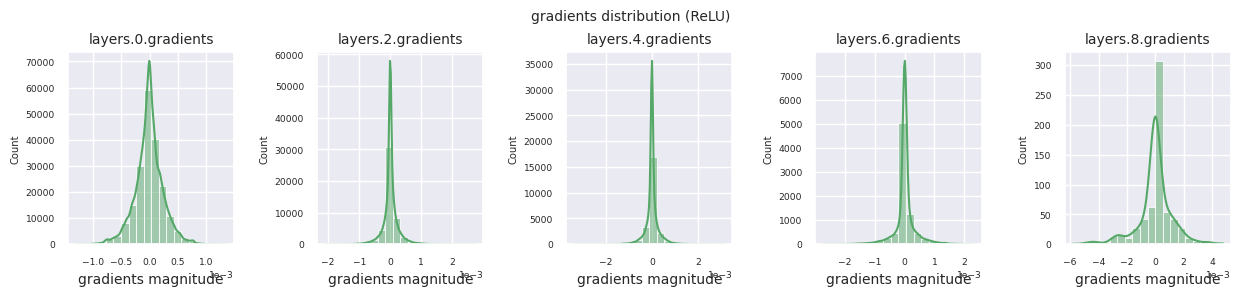
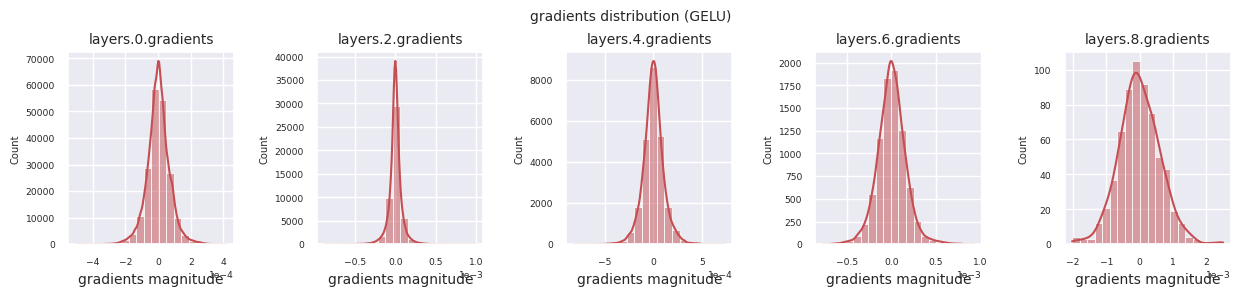
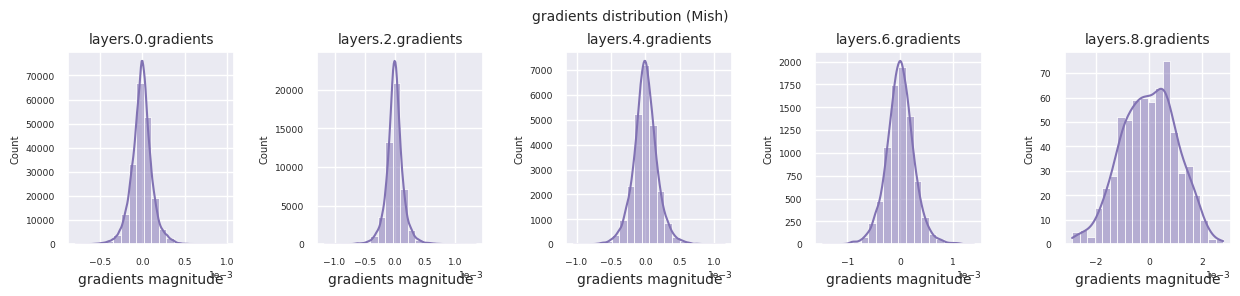
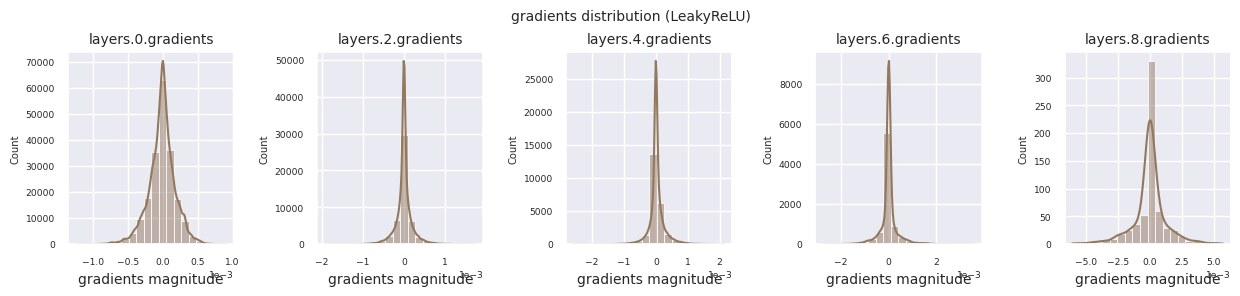
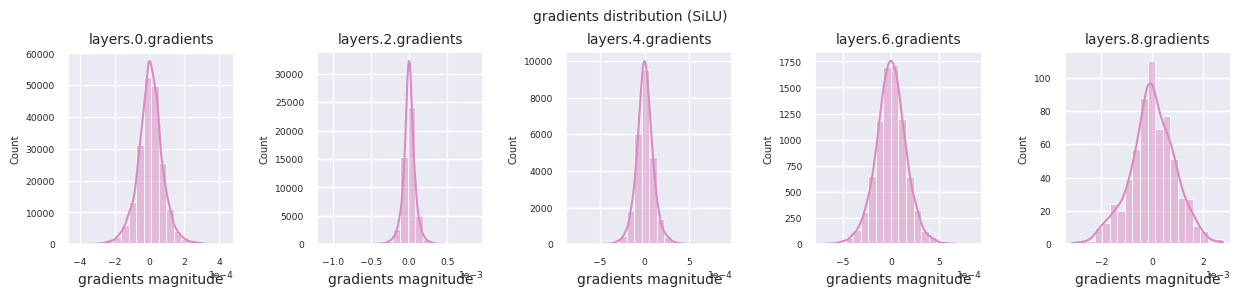
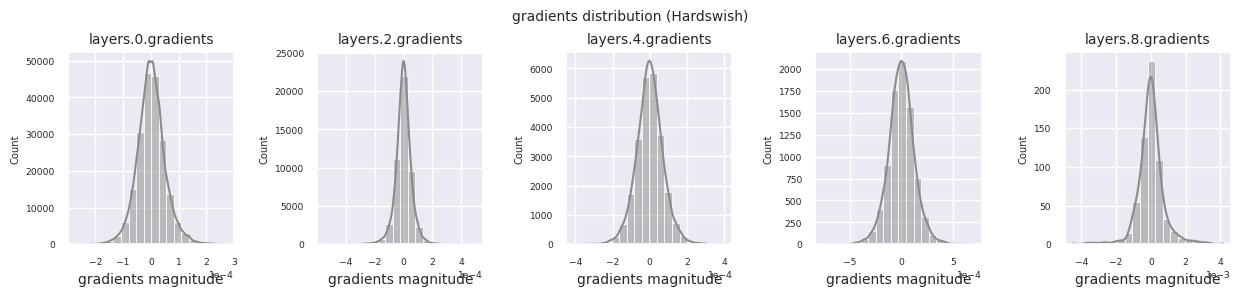
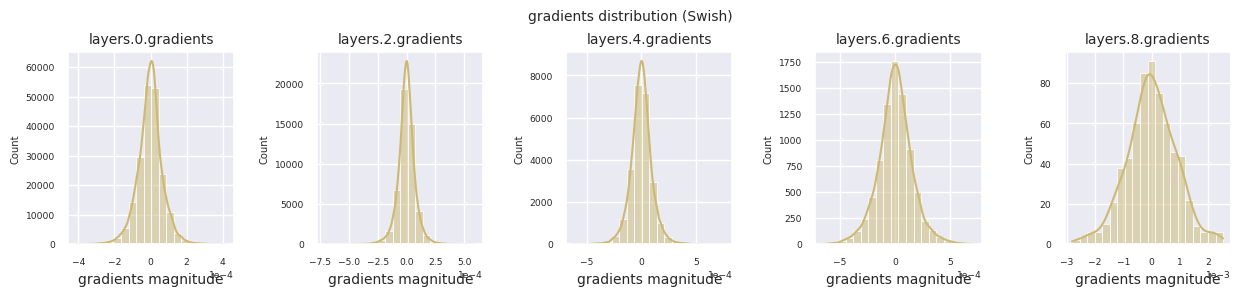
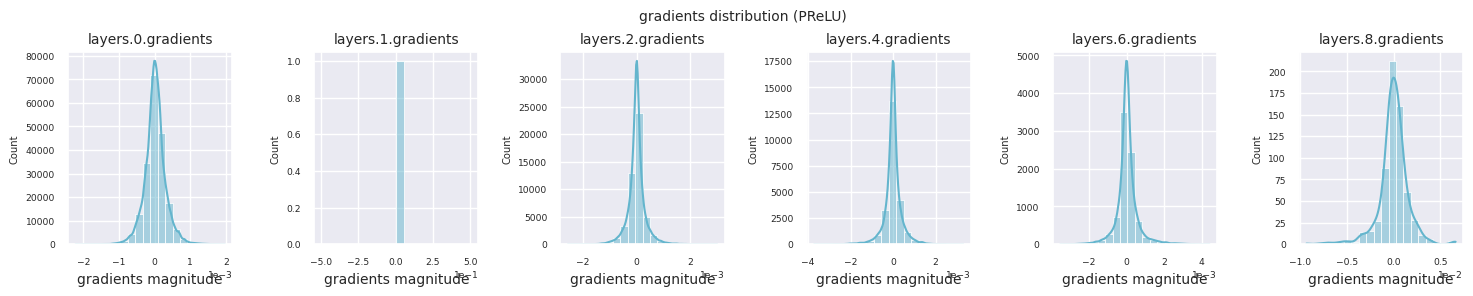
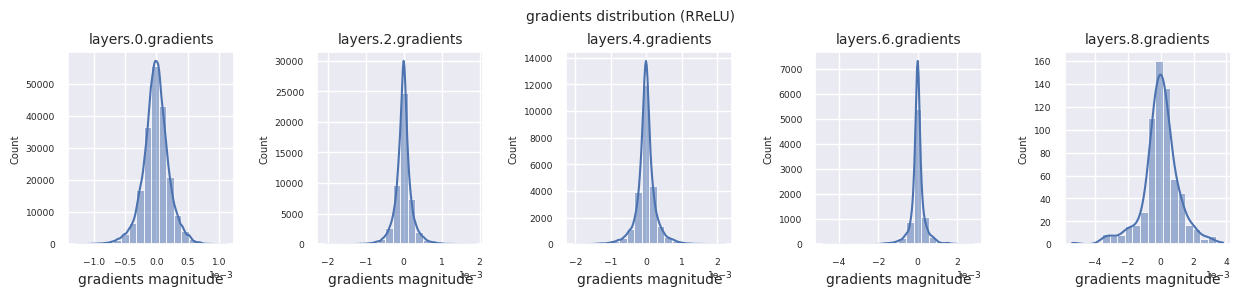
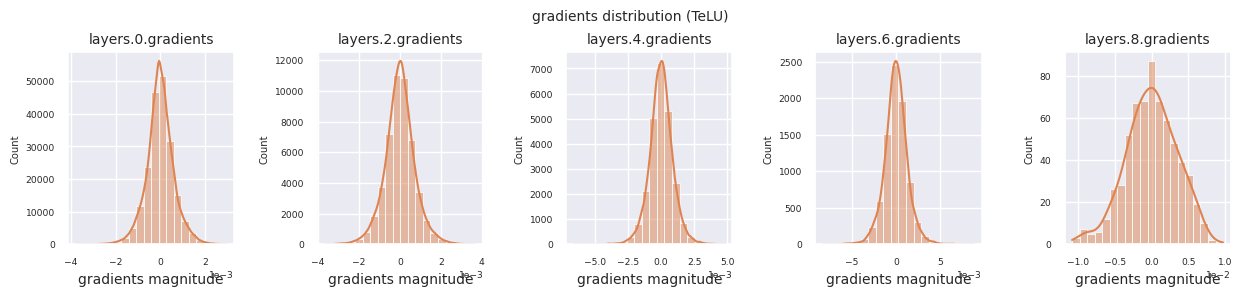
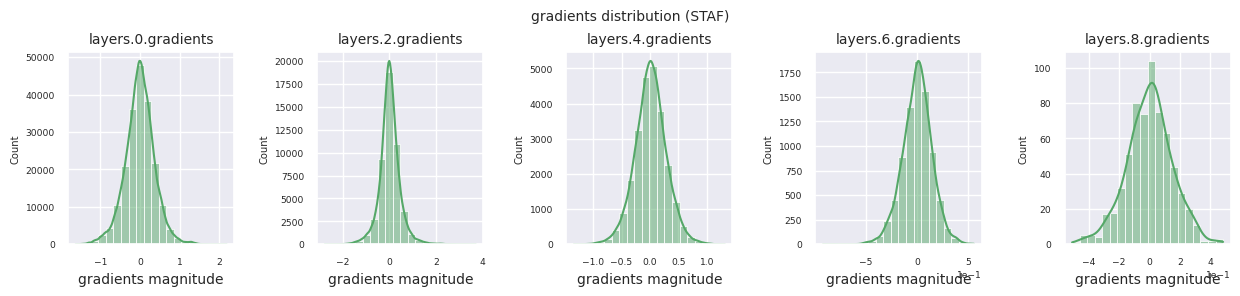
观察不同激活函数的梯度分布，可以发现Sigmoid在输入层显示出\(10^{-5}\)量级的非常小的值，可能会导致梯度消失问题。ReLU的梯度集中在0附近，这是因为它对负输入具有非激活（死亡神经元）特性。最新的自适应激活函数在缓解这些问题的同时保持了非线性。例如，GELU显示出接近正态分布的梯度分布，这与批归一化结合时效果良好。让我们将其与没有激活函数的情况进行比较。

Code

from dldna.chapter_04.models.base import SimpleNetwork

model_no_act = SimpleNetwork(act_func=nn.ReLU(), no_act = True).to(device) 

gradients, weights = get_gradients_weights(model_no_act, train_dataloader)

visualize_distribution(model_no_act, gradients, title="gradients")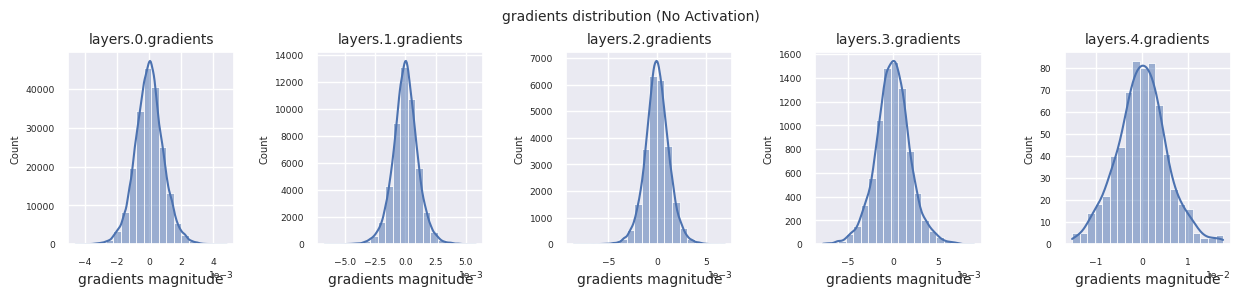

如果没有激活函数，层间的分布将相似，只是规模发生变化。这表明没有非线性，层间特征变换是有限的。

4.4 模型训练

为了客观地比较激活函数的性能，我们使用FashionMNIST数据集进行实验。截至2025年，存在500多个激活函数，但在实际的深度学习项目中，主要使用的是一些经过验证的少数激活函数。首先，我们将以ReLU为基准，查看基本的训练过程。

4.4.1 单模型训练

Code

import torch.optim as optim
from dldna.chapter_04.experiments.model_training import train_model
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_device
from dldna.chapter_04.visualization.training import plot_results

model = SimpleNetwork(act_func=nn.ReLU()).to(device)
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
results = train_model(model, train_dataloader, test_dataloader, device, epochs=10)
plot_results(results)


Starting training for SimpleNetwork-ReLU.

Execution completed for SimpleNetwork-ReLU, Execution time = 76.1 secs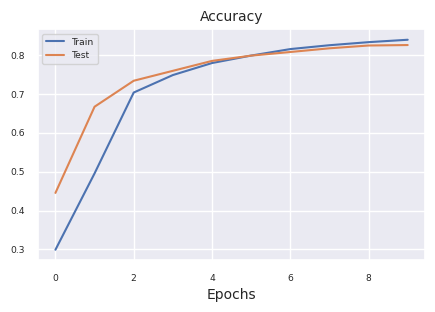

4.4.2 根据激活函数进行模型训练

现在对主要的激活函数进行比较实验。保持每个模型的结构和训练条件相同，以确保公平比较。 - 4个隐藏层 [256, 192, 128, 64] - SGD 优化器 (learning rate=1e-3, momentum=0.9) - 批量大小 128 - 训练 15 个 epoch

Code

from dldna.chapter_04.experiments.model_training import train_all_models
from dldna.chapter_04.visualization.training import create_results_table


from dldna.chapter_04.experiments.model_training import train_all_models
from dldna.chapter_04.visualization.training import create_results_table  # Assuming this is where plot functions are.

# Train only selected models
# selected_acts = ["ReLU"]  # Select only the desired activation functions
selected_acts = ["Tanh", "ReLU", "Swish"]
# selected_acts = ["Sigmoid", "ReLU", "Swish", "PReLU", "TeLU", "STAF"]
# selected_acts = ["Sigmoid", "Tanh", "ReLU", "GELU", "Mish", "LeakyReLU", "SiLU", "Hardswish", "Swish", "PReLU", "RReLU", "TeLU", "STAF"]
# results_dict = train_all_models(act_functions, train_dataloader, test_dataloader,
#                               device, epochs=15, selected_acts=selected_acts)
results_dict = train_all_models(act_functions, train_dataloader, test_dataloader,
                              device, epochs=15, selected_acts=selected_acts, save_epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15])

create_results_table(results_dict)

如下表所示。根据各自的执行环境，值会有所不同。

模型	准确度(%)	最终误差(%)	耗时 (秒)
SimpleNetwork-Sigmoid	10.0	2.30	115.6
SimpleNetwork-Tanh	82.3	0.50	114.3
SimpleNetwork-ReLU	81.3	0.52	115.2
SimpleNetwork-GELU	80.5	0.54	115.2
SimpleNetwork-Mish	81.9	0.51	113.4
SimpleNetwork-LeakyReLU	80.8	0.55	114.4
SimpleNetwork-SiLU	78.3	0.59	114.3
SimpleNetwork-Hardswish	76.7	0.64	114.5
SimpleNetwork-Swish	78.5	0.59	116.1
SimpleNetwork-PReLU	86.0	0.40	114.9
SimpleNetwork-RReLU	81.5	0.52	114.6
SimpleNetwork-TeLU	86.2	0.39	119.6
SimpleNetwork-STAF	85.4	0.44	270.2

分析实验结果：

计算效率：Tanh, ReLU 等最快，而 STAF 因复杂的运算相对最慢。
准确度：
- 自适应激活函数（TeLU 86.2%，PReLU 86.0%，STAF 85.4%）总体表现优异。
- 经典的 Sigmoid 因梯度消失问题性能极低（10.0%）。
- 现代基础激活函数（ReLU, GELU, Mish）表现出稳定的 80-82% 范围内的性能。
稳定性：
- Tanh, ReLU, Mish 表现出相对稳定的训练曲线。
- 自适应激活函数虽然表现高，但在学习过程中波动性更大。

这些结果是在特定条件下的对比，实际项目中选择激活函数时应考虑以下因素。1. 与模型架构的兼容性（例如：Transformer 推荐使用 GELU）2. 计算资源的限制（移动环境中考虑使用 Hardswish）3. 任务特性（时间序列预测中 Tanh 仍然有用）4. 模型大小和数据集特性

截至 2025 年，大规模语言模型为提高计算效率通常使用 GELU，计算机视觉领域常使用 ReLU 类激活函数，强化学习则主要采用自适应激活函数。

4.5 训练模型的逐层输出和非激活神经元分析

前面我们观察了初始模型在反向传播中各层梯度值的分布。现在我们将使用训练好的模型来查看前向计算中各层输出什么值。分析训练模型各层的输出对于理解神经网络的表现力和学习模式非常重要。自2010年引入ReLU以来，非激活神经元问题已成为深度神经网络设计的主要考虑因素。

首先我们可视化训练模型在前向计算中各层的输出分布。

4.5.1 逐层输出分布可视化

Code

import os
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_04.visualization.gradients import get_model_outputs, visualize_distribution


device = get_device()
# Re-define the data loaders.
train_dataloader, test_dataloader = get_data_loaders()

for i, act_func in enumerate(act_functions):
    model_file = f"SimpleNetwork-{act_func}.pth"
    model_path = os.path.join("./tmp/models", model_file)
    
    # Load the model only if the file exists
    if os.path.exists(model_path):
        # Load the model.
        model, config = load_model(model_file=model_file, path="./tmp/models")
        layer_outputs = get_model_outputs(model, test_dataloader, device)

        visualize_distribution(model, layer_outputs, title="gradients", color=f"C{i}")
    else:
        print(f"Model file not found: {model_file}")

4.5.2 非活跃神经元的问题

非活跃神经元（死亡神经元）是指对所有输入始终输出0的神经元。这在ReLU系列激活函数中是一个重要的问题。要找到非活跃神经元，可以将所有训练数据通过网络，并找出始终输出0的神经元。为此，可以使用逻辑运算对每个层的输出值进行掩码处理，以确定是否始终为0。

Code

# 3 samples (1 batch), 5 columns (each a neuron's output). Columns 1 and 3 always show 0.
batch_1 = torch.tensor([[0, 1.5, 0, 1, 1],
                        [0, 0,  0, 0, 1],
                        [0, 1,  0, 1.2, 1]])

# Column 3 always shows 0
batch_2 = torch.tensor([[1.1, 1, 0, 1, 1],
                        [1,   0, 0, 0, 1],
                        [0,   1, 0, 1, 1]])

print(batch_1)
print(batch_2)

# Use the .all() method to create a boolean tensor indicating which columns
# have all zeros along the batch dimension (dim=0).
batch_1_all_zeros = (batch_1 == 0).all(dim=0)
batch_2_all_zeros = (batch_2 == 0).all(dim=0)

print(batch_1_all_zeros)
print(batch_2_all_zeros)

# Declare a masked_array that can be compared across the entire batch.
# Initialized to all True.
masked_array = torch.ones(5, dtype=torch.bool)
print(f"masked_array = {masked_array}")

# Perform logical AND operations between the masked_array and the all_zeros
# tensors for each batch.
masked_array = torch.logical_and(masked_array, batch_1_all_zeros)
print(masked_array)
masked_array = torch.logical_and(masked_array, batch_2_all_zeros)
print(f"final = {masked_array}")  # Finally, only the 3rd neuron remains True (dead neuron).

tensor([[0.0000, 1.5000, 0.0000, 1.0000, 1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
        [0.0000, 1.0000, 0.0000, 1.2000, 1.0000]])
tensor([[1.1000, 1.0000, 0.0000, 1.0000, 1.0000],
        [1.0000, 0.0000, 0.0000, 0.0000, 1.0000],
        [0.0000, 1.0000, 0.0000, 1.0000, 1.0000]])
tensor([ True, False,  True, False, False])
tensor([False, False,  True, False, False])
masked_array = tensor([True, True, True, True, True])
tensor([ True, False,  True, False, False])
final = tensor([False, False,  True, False, False])

计算非活动神经元的函数是 calculate_disabled_neuron。它位于 visualization/training.py 中。我们将分析实际模型中非活动神经元的比例。

Code

from dldna.chapter_04.visualization.training import calculate_disabled_neuron
from dldna.chapter_04.models.base import SimpleNetwork

# Find in the trained model.
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="./tmp/models")
calculate_disabled_neuron(model, train_dataloader, device)

model, _ = load_model(model_file="SimpleNetwork-Swish.pth", path="./tmp/models")
calculate_disabled_neuron(model, train_dataloader, device)

# Change the size of the model and compare whether it also occurs at initial values.
big_model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[2048, 1024, 1024, 512, 512, 256, 128]).to(device)
calculate_disabled_neuron(big_model, train_dataloader, device)


Number of layers to compare = 4

Number of disabled neurons (ReLU) : [0, 6, 13, 5]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 3.1%
Ratio of disabled neurons = 10.2%
Ratio of disabled neurons = 7.8%

Number of layers to compare = 4

Number of disabled neurons (Swish) : [0, 0, 0, 0]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%

Number of layers to compare = 7

Number of disabled neurons (ReLU) : [0, 0, 6, 15, 113, 102, 58]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.6%
Ratio of disabled neurons = 2.9%
Ratio of disabled neurons = 22.1%
Ratio of disabled neurons = 39.8%
Ratio of disabled neurons = 45.3%

根据目前的研究结果，非激活神经元问题的严重性会随着模型深度和宽度的不同而变化。特别值得注意的是： 1. 模型越深，ReLU 的非激活神经元比例急剧增加 2. 自适应激活函数（STAF, TeLU）可以有效缓解这一问题 3. Transformer 架构中，GELU 大幅减少了非激活神经元问题 4. 最新的 MoE（Mixture of Experts）模型通过为每个专家网络使用不同的激活函数来解决问题

因此，在设计层数较多的神经网络时应考虑使用 GELU、STAF、TeLU 等替代 ReLU，特别是在超大规模模型中需要综合考虑计算效率和非激活神经元问题。

4.6 确定激活函数候选

选择激活函数是神经网络设计中非常重要的决策之一。激活函数直接影响网络学习复杂模式的能力、训练速度和整体性能。以下是根据最新研究成果及应用领域的最佳实践整理的内容。

计算机视觉 (Computer Vision)

基于CNN的模型: ReLU及其变体（LeakyReLU, PReLU, ELU）仍然广泛使用，因为它们计算效率高且通常表现良好。然而，在更深层次的架构中，特别是追求高性能的CNN中，GELU和Swish/SiLU越来越被采用，因为它们具有更平滑的梯度。
视觉变压器 (ViTs): GELU在ViT中实际上已成为标准。这与自然语言处理领域中的Transformer成功使用GELU相呼应。
移动/嵌入式设备: Hardswish由于提供了计算效率而在资源受限环境中受到青睐。ReLU及其变体（如MobileNets中常用的ReLU6等）仍然是强大的选项。
生成模型 (高精度图像生成): STAF显示出有希望的结果，但尚未广泛采用。Swish、GELU和Mish等平滑激活函数在生成任务中更受青睐，因为它们倾向于产生更高品质的输出并减少伪影。目前最先进的图像生成模型（如Diffusion模型）经常使用Swish/SiLU。

自然语言处理 (NLP)

基于Transformer的模型: 在大多数Transformer架构（BERT, GPT等）中，GELU是主导选择。
RNN/LSTM: 传统上首选Tanh，但为了更好地缓解梯度消失问题，正逐渐被其他激活函数替代。在最新的RNN/LSTM实现中，经常使用GELU及ReLU变体（谨慎的初始化和正则化技术配合）。
大规模语言模型 (LLMs): 计算效率最为重要。GELU和ReLU（或GELU的快速近似）是最常见的选择。一些LLM在混合专家(Mixture-of-Experts, MoE)层内尝试特殊激活函数。

语音处理 (Speech Processing)

情感识别: TeLU显示出有希望的结果，但尚未成为广泛使用的标准。ReLU变体、GELU和Swish/SiLU是强大的通用候选者。最佳选择取决于特定的数据集和模型架构。
语音合成: Snake和GELU等平滑激活有助于生成更自然的语音，因此经常被推荐。
实时处理: 类似于移动视觉，Hardswish及ReLU变体适合要求低延迟的应用程序。

一般建议和最新趋势

以下是选择激活函数候选的更为系统的方法。

基本选择（良好的起点）:
- GELU: 尤其适用于Transformer及更深层次网络的通用优秀选择。
- ReLU (或LeakyReLU/PReLU): 对于CNN仍然是强大且高效的选项。为避免“Dying ReLU”问题，可以考虑使用LeakyReLU或PReLU。
- Swish/SiLU: 在更深的网络中通常比ReLU表现更优，并在多方面表现出色。
高性能（潜在更高的计算成本）:
- Mish: 通常能够达到顶级结果，但计算成本高于 ReLU 或 GELU。
- TeLU: 是 ELU 的可学习变体。关于更快的收敛和稳定性的主张值得验证，但尚未广泛采用。基准测试是关键。
- 有理激活函数: 具有近似复杂函数和处理动态系统的能力，在强化学习及基于物理的神经网络(PINN)中前景广阔。但在标准监督学习任务中使用较少。
轻量/高效:
- Hardswish: 专为移动和嵌入式设备设计。
- ReLU6: 是将输出范围限制在6内的 ReLU 变体，常用于量化模型。
自适应/可学习:
- PReLU: 学习负斜率参数。简单且有效。
- TeLU: 学习 ELU 函数指数部分的缩放因子。
- STAF: 在复杂模式捕捉上显示出潜力，但 STAF（及其他傅里叶基激活）计算成本高，并未在大多数通用任务中证明比更简单的选项有持续优势。依然是活跃的研究领域。
- B-spline: 具有局部控制属性，但 B-spline 激活（与 STAF 类似）由于复杂性，在主流深度学习中不常见。更多出现在曲线拟合或几何建模等特殊应用中。这是一个活跃的研究领域，并且在连续/渐进学习(continual/incremental learning)方面可能有效，但尚未广泛确立。

最新主要趋势和考虑因素:

深网络中 Sigmoid/Tanh 使用减少: 由于梯度消失问题，在现代深度网络中几乎不作为隐藏层激活使用。
平滑性的重要性: 平滑的激活函数（如 GELU, Swish, Mish）通常在更深的网络中比非平滑函数（ReLU）更受欢迎。这往往导致更稳定的训练和更好的梯度流动。
计算成本: 特别是在大型模型或资源受限设备的情况下，始终考虑激活函数的计算成本。
任务特定性: 最佳激活函数可能因任务而异。实验很重要。
专家混合 (Mixture of Experts, MoE): 在一些像某些 LLM 这样的非常大的模型中，不同的“专家”子网络可以使用不同的激活函数。
有理激活函数与动态系统: 有理激活函数及其“联合-有理”扩展学习和表达系统动力学的能力是有前途的研究方向。

最重要的是，始终进行实验！ 从合理默认值（如 GELU 或 ReLU/LeakyReLU）开始，如果未达到预期性能，则准备好尝试其他选项。在保持其他超参数不变的情况下仅更改激活函数的小规模实验对于做出知情选择是必不可少的。

点击查看内容（深入探讨：设计自己的激活函数）

深入探讨：设计自己的激活函数 - 理论与实践

激活函数是深度学习模型的核心组成部分之一，对模型的表达能力、学习速度以及最终性能有重大影响。除了广泛使用的激活函数（ReLU、GELU、Swish等）之外，许多研究人员还提出了新的激活函数。在本深入探讨中，我们将逐步了解设计自己激活函数的过程，并学习如何使用PyTorch实现和测试这些函数。

1. 激活函数设计的基本原则

在设计新的激活函数之前，让我们再次回顾4.2节中描述的“理想”激活函数的条件。

非线性 (Non-linearity): 使神经网络能够表达（近似）复杂函数。
可微分性 (Differentiability): 是通过反向传播算法训练神经网络所必需的。（允许在某些点如ReLU处不可微）
防止梯度消失/爆炸问题: 确保深度神经网络中的学习过程稳定进行。
计算效率 (Computational Efficiency): 影响神经网络的学习和推理速度。

除此之外，还可以考虑以下事项。

零中心输出 (Zero-Centered Output): 激活函数的输出以0为中心分布可以提高学习速度。（如Tanh、ELU等）
自门控 (Self-Gating): 由输入值本身调节激活程度的特性。（如Swish）
平滑性 (Smoothness): 平滑（smooth）的激活函数通常会导致更稳定的训练。
单调性 (Monotonicity): 单调函数是随着输入增加，输出也增加或减少的函数。ReLU、Leaky ReLU、ELU、GELU、Swish、Mish都是单调函数。Sigmoid和Tanh则不是单调函数。单调性可以简化优化过程，但并不是必需条件。
有界性 (Boundedness): 激活函数的输出是否被限制在特定范围内。Sigmoid和Tanh是有界的函数，而ReLU系列则是无界的。有界函数有助于防止梯度爆炸，但也可能限制表达能力。

2. 创意生成：现有激活函数的组合与变体

设计新的激活函数最常见的方法是结合或修改现有的激活函数。

ReLU系列变体: 为了解决ReLU的“Dying ReLU”问题，提出了Leaky ReLU、PReLU、ELU、SELU等不同变体。可以扩展这些想法，考虑改变负区域的行为，或者添加可学习的参数。
Sigmoid/Tanh系列变体: 为了缓解梯度消失问题，可以修改Sigmoid或Tanh函数，或将它们与其他函数结合。
Swish/Mish系列: 具有自门控特性的Swish(\(x \cdot sigmoid(x)\))和Mish(\(x \cdot tanh(ln(1 + e^x))\))被认为表现出良好的性能。可以考虑改变这些函数的形式或与其它函数结合的方法。
GELU变体: GELU在Transformer模型中被广泛使用。可以通过变形GELU的近似式，或将它与其他函数组合来创建新的激活函数。

3. 数学分析：可微分性、梯度特性

如果提出了新的激活函数，则必须进行数学分析。

可微性： 必须确认所提出的函数在所有区间内是否可微，或者像ReLU一样，在某些点不可微但可以定义次梯度。使用PyTorch的自动微分功能来计算导数值并绘制图形将有所帮助。
梯度特性： 必须分析根据输入值范围梯度如何变化。必须确认是否存在梯度过小（vanishing gradient）或过大的区域（exploding gradient）。

4. PyTorch实现

通过数学分析验证了有效性的激活函数可以使用PyTorch轻松实现。继承torch.nn.Module创建新类，并在forward方法中定义激活函数的运算即可。必要时，可以用torch.nn.Parameter定义可学习参数。

示例： “SwiGELU” 激活函数实现

我们提出了一种结合了Swish和GELU的新激活函数“SwiGELU”，并用PyTorch实现它。（来自练习题4.2.3的答案）

import torch
import torch.nn as nn
import torch.nn.functional as F

class SwiGELU(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x):
        return 0.5 * (x * torch.sigmoid(x) + F.gelu(x))

说明：

SwiGELU(x) = 0.5 * (x * sigmoid(x) + GELU(x))
将Swish(\(x \cdot sigmoid(x)\))和GELU(\(x\Phi(x)\))以1:1的比例结合，并乘以0.5来调整输出值的范围。
预期可以同时利用Swish的自我门控特性和GELU的平滑非线性及正则化效果。

5. 实验与评估

如果提出了新的激活函数，则应使用基准数据集（例如，CIFAR-10、CIFAR-100、ImageNet）进行实验以比较其与现有激活函数的性能。

实验设置：
- 使用相同的模型架构，并仅更改激活函数来运行实验。
- 保持学习率、批大小、优化器等其他超参数相同。
- 反复多次实验以确保结果的统计显著性。
评估指标：
- Accuracy（准确度）
- Loss
- Training Time（训练时间）
- Convergence Speed（收敛速度）
- Gradient Norm（梯度大小）- 利用train_model_with_metrics函数
- Number/Percentage of Disabled Neurons（“死亡神经元”比例）- 利用calculate_disabled_neuron函数
- 如有需要，还包括内存使用量等
结果分析
- 定量比较收敛速度和最终性能
- 是否发生梯度消失/爆炸问题
- “死亡神经元”发生的比例是多少

6. （可选）理论分析

如果实验结果良好，则最好从理论上分析为什么新的激活函数表现出色。 * 损失景观分析: 分析激活函数对损失函数空间(loss landscape)的影响。 (参见4.2节深入探讨) * 神经切线核(NTK)分析: 在无限宽的神经网络中分析激活函数的作用。 * 福克-普朗克方程: 分析激活函数的动力学特性。 (参考Swish的研究)

结论

设计和评估新的激活函数是一项艰巨的任务，但它是提高深度学习模型性能的一个潜力巨大的研究领域。克服现有激活函数的局限性，并找到更适合特定问题或架构的激活函数是深度学习研究中的一个重要任务。希望本深入探讨中提出的逐步方法、PyTorch实现示例以及实验和分析指南能帮助您设计自己的激活函数。

点击查看内容（深入探讨：自适应激活函数 - 未来研究方向）

深入探讨：自适应激活函数 - 未来研究方向

引言:

ReLU、GELU 等固定的激活函数在深度学习模型中被广泛使用，但它们可能不适用于特定问题或数据分布。最近，根据数据或任务调整激活函数的 自适应 研究正在蓬勃发展。本文将探讨自适应激活函数（Adaptive Activation Function）的潜力和未来研究方向。

1. 自适应激活函数的类型

自适应激活函数大致可以分为以下几类：

基于参数的自适应 (Parametric Adaptation): 引入可学习的参数到激活函数中，根据数据调整函数的形式。
- 示例:
  - Leaky ReLU: \(f(x) = max(\alpha x, x)\) (\(\alpha\) 是可学习的参数)
  - PReLU (Parametric ReLU): 在 Leaky ReLU 中每个通道分别学习 \(\alpha\)
  - Swish: \(f(x) = x \cdot \sigma(\beta x)\) (\(\beta\) 是可学习的参数)
结构自适应 (Structural Adaptation): 通过组合多个基函数（basis function）或改变网络结构来动态构建激活函数。
- 示例:
  - Maxout Networks: 从多个线性函数中取最大值
  - 基于样条的激活函数 (Spline-based Activation Functions): 使用样条函数表示激活函数
基于输入的自适应: 根据输入数据的特性改变或混合激活函数
- 示例:
  - Squeeze and Excitation(SE) Block: 计算输入特征图各通道的重要性，并为激活函数分配权重

2. 可能的研究方向

2.1 基于专家混合 (Mixture of Experts, MoE) 的激活函数

想法: 定义多个“专家”激活函数，并根据输入数据动态决定每个专家的权重。
数学表示:

\(f(x) = \sum_{k=1}^K g_k(x) \cdot \phi_k(x)\)
- \(g_k(x)\): 输入 \(x\) 对应的第 \(k\) 个专家激活函数的门控函数（通常通过 softmax 等方法进行归一化）
- \(\phi_k(x)\): 第 \(k\) 个专家激活函数（可以使用 ReLU、GELU、Swish 等多种函数）
研究课题:
- 高效的门控机制: 研究计算 \(g_k(x)\) 的高效方法（例如：Top-k 门控，稀疏门控）
- 专家激活函数选择: 研究使用哪种类型的 \(\phi_k(x)\) 更好，以及如何确定专家的数量
- 理论分析: 对 MoE 激活函数的表达能力（expressive power）和泛化性能进行理论分析

2.2 与神经网络结构搜索 (Neural Architecture Search, NAS) 的结合

想法: 使用NAS自动探索与数据和任务最优化的激活函数结构。
方法:
- 搜索空间 (Search Space):
  - 定义基本运算（线性变换、指数函数、对数函数、三角函数等）
  - 定义可以通过组合这些运算生成的各种激活函数候选
- 搜索策略 (Search Strategy):
  - 强化学习 (Reinforcement Learning)
  - 进化算法 (Evolutionary Algorithm)
  - 可微架构搜索 (Differentiable Architecture Search, DARTS)
- 性能评估 (Performance Estimation):
  - 训练包含所搜索的激活函数的模型，并在验证数据集上进行性能评估
研究课题:
- 高效搜索空间设计: 定义一个既不太大又能包含足够多样的激活函数的搜索空间
- 降低计算成本: NAS的计算成本非常高，因此需要开发高效的搜索策略和性能评估方法

2.3 物理/生物信息整合

想法: 利用物理学、生物学等领域的知识，在设计激活函数时加入约束条件或先验知识。
示例:
- 物理模型: 在建模特定物理系统时，将该系统的微分方程反映在激活函数中
- 神经科学: 模仿实际神经元的工作方式的激活函数（例如：脉冲神经元模型）
研究课题:
- 领域知识的有效整合: 开发如何将领域知识反映到激活函数设计中的方法论
- 泛化性能: 验证特定领域的激活函数是否在其他领域也能良好工作

2.4 加强理论分析

表达力 (Expressive Power): 分析自适应激活函数相比于传统激活函数具有多强大的表达能力
优化便捷性 (Optimization Landscape): 分析自适应激活函数如何改变损失函数表面(loss landscape)，以及这对学习速度和稳定性的影响
泛化性能 (Generalization): 分析自适应激活函数是否能防止过拟合(overfitting)并提高泛化性能

3. 结论与建议

自适应激活函数是提升深度学习模型性能的一个有前途的研究领域。然而，以下问题仍然存在。

计算复杂度: 自适应激活函数通常比固定的激活函数具有更高的计算成本。
可解释性: 学习到的激活函数形式变得复杂时，模型的可解释性可能会降低。
过拟合风险: 过于灵活的激活函数有在训练数据上过拟合的风险。

未来的研究应着重解决这些问题，同时开发更高效、可解释且泛化性能优秀的自适应激活函数。

练习题

4.2.1 基本问题

写出 Sigmoid、Tanh、ReLU、Leaky ReLU、GELU、Swish 函数的公式，并绘制其图形。 (可使用 matplotlib, Desmos 等工具)
- 参考: 清晰理解每个函数的定义和特性，通过图形进行直观比较。
求出各激活函数的导数（微分），并绘制其图形。
- 参考: 导数用于反向传播过程中计算梯度。了解每个函数的可微性和梯度特征。
使用 FashionMNIST 数据集，训练一个仅包含线性变换而不使用激活函数的神经网络，并测量测试准确率。 (利用第1章实现的 SimpleNetwork)
- 参考: 没有激活函数的神经网络无法表示非线性，因此在解决复杂问题时存在局限性。通过实验来验证这一点。
将第3题的结果与使用 ReLU 激活函数的神经网络的结果进行比较，并解释激活函数的作用。
- 参考: 分别从各层输出值、梯度和不活跃神经元等方面进行对比，以说明有无激活函数的情况。

4.2.2 应用问题

使用 PyTorch 实现 PReLU、TeLU、STAF 激活函数。 (继承自 nn.Module)
- 参考: 参考每个函数的定义实现 forward 方法，如有需要，使用 nn.Parameter 定义可学习参数。
使用 FashionMNIST 数据集训练包含前面实现的激活函数的神经网络，并比较测试准确率。
- 参考: 比较各激活函数的性能，分析哪种函数更适合 FashionMNIST 数据集。
对每个激活函数，在训练过程中可视化梯度分布，并测量“死亡神经元”的比例。 (利用第1章实现的函数)
- 参考: 分别针对每个激活函数，将梯度分布与初始值、训练后的值以及各层之间的差异以图形形式进行可视化。
调查缓解“死亡神经元”问题的方法，并解释其原理。 (Leaky ReLU, PReLU, ELU, SELU 等)
- 参考: 说明每种方法如何解决 ReLU 的问题，以及各自的优缺点。

4.2.3 深化问题

使用 PyTorch 实现 Rational 激活函数，并解释其特点和优缺点。
- 参考: Rational 激活函数基于有理函数（分数函数），在某些问题中可能表现出优于其他激活函数的性能。
使用 PyTorch 实现 B-spline 激活函数或 Fourier-based 激活函数，并解释其特点和优缺点。
- 参考: B-spline 激活函数可以表示局部可控的灵活曲线，而 Fourier-based 激活函数在建模周期性模式方面具有优势。
提出一种新的激活函数，与现有激活函数进行性能对比评估。 (附带实验结果和理论依据)
- 参考: 在设计新激活函数时，应考虑理想激活函数的条件（非线性、可微分性、防止梯度消失/爆炸问题、计算效率等）。

点击查看内容（答案）

练习题解答

4.2.1 基本问题

Sigmoid, Tanh, ReLU, Leaky ReLU, GELU, Swish 函数的公式及图形:

激活函数	公式	图形 (参考)
Sigmoid	\(\sigma(x) = \frac{1}{1 + e^{-x}}\)	Sigmoid
Tanh	\(tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\)	Tanh
ReLU	\(ReLU(x) = max(0, x)\)	ReLU
Leaky ReLU	\(LeakyReLU(x) = max(ax, x)\) , (\(a\)是小常数，通常为0.01)	(Leaky ReLU在ReLU图形的x < 0部分有小斜率(\(a\)))
GELU	\(GELU(x) = x\Phi(x)\) , (\(\Phi(x)\)是高斯累积分布函数)	GELU
Swish	\(Swish(x) = x \cdot sigmoid(\beta x)\) , (\(\beta\)是常数或学习参数)	Swish

各激活函数的导数: | 激活函数 | 导数 | | :———- | :—————————————————————————————— | | Sigmoid | \(\sigma'(x) = \sigma(x)(1 - \sigma(x))\) | | Tanh | \(tanh'(x) = 1 - tanh^2(x)\) | | ReLU | \(ReLU'(x) = \begin{cases} 0, & x < 0 \\ 1, & x > 0 \end{cases}\) | | Leaky ReLU | \(LeakyReLU'(x) = \begin{cases} a, & x < 0 \\ 1, & x > 0 \end{cases}\) | | GELU | \(GELU'(x) = \Phi(x) + x\phi(x)\), (\(\phi(x)\)是高斯概率密度函数) | | Swish | \(Swish'(x) = sigmoid(\beta x) + x \cdot sigmoid(\beta x)(1 - sigmoid(\beta x))\beta\) |
FashionMNIST，无激活函数的神经网络训练及准确度测量:
- 由于没有激活函数，该神经网络仅执行线性变换，因此无法建模复杂的非线性关系。在像FashionMNIST这样复杂的数据集上表现较低的准确性。（大约10%左右的准确性）
使用ReLU激活函数的神经网络与无激活函数的比较，解释激活函数的作用:
- 使用ReLU激活函数的神经网络通过引入非线性可以实现更高的准确性。（80%以上的准确性）
- 每层输出值: 没有激活函数时，每层的输出分布仅显示简单的尺度变化；使用ReLU后，负值被抑制为0，导致分布发生变化。
- 梯度: 没有激活函数时，梯度简单传递；使用ReLU后，对于负输入，梯度变为0，不再传播。
- 不活跃神经元: 在没有激活函数的情况下不会发生，但在使用ReLU时可能发生
- 作用总结: 激活函数通过赋予神经网络非线性能力来近似复杂函数，并调节梯度流以辅助学习。

4.2.2 应用问题

PReLU, TeLU, STAF PyTorch实现:

import torch
import torch.nn as nn

class PReLU(nn.Module):
    def __init__(self, num_parameters=1, init=0.25):
        super().__init__()
        self.alpha = nn.Parameter(torch.full((num_parameters,), init))

    def forward(self, x):
        return torch.max(torch.zeros_like(x), x) + self.alpha * torch.min(torch.zeros_like(x), x)

```python class TeLU(nn.Module): def init(self, alpha=1.0): super().__init__() self.alpha = nn.Parameter(torch.tensor(alpha))

def forward(self, x): return torch.where(x > 0, x, self.alpha * (torch.exp(x) - 1))

class STAF(nn.Module): def init(self, tau=25): super().__init__() self.tau = tau self.C = nn.Parameter(torch.randn(tau)) self.Omega = nn.Parameter(torch.randn(tau)) self.Phi = nn.Parameter(torch.randn(tau))

def forward(self, x):
    result = torch.zeros_like(x)
    for i in range(self.tau):
        result += self.C[i] * torch.sin(self.Omega[i] * x + self.Phi[i])
    return result


2.  **FashionMNIST, 激活函数比较实验:**

    *   训练包含PReLU、TeLU和STAF的神经网络，并比较测试准确率。
    *   实验结果显示，自适应激活函数（PReLU、TeLU、STAF）比ReLU具有更高的准确性。（顺序为：STAF > TeLU > PReLU > ReLU）

3.  **梯度分布可视化，“死神经元”比率测量:**

     *  ReLU在负输入时梯度为0，而PReLU、TeLU和STAF即使在负输入时也能传递小的梯度值。
    *   “死神经元”的比率在ReLU中最高，在PReLU、TeLU和STAF中较低。

4.  **缓解“死神经元”问题的方法及其原理:**

    *   **Leaky ReLU:** 允许对负输入有微小的斜率，以防止神经元完全失活。
    *   **PReLU:** 将Leaky ReLU的斜率变为可学习参数，根据数据找到最佳斜率。
    *   **ELU, SELU:** 在负区域保持非零值，并且具有平滑曲线形状，从而缓解梯度消失问题并稳定学习过程。

### 4.2.3 深化问题

1.  **Rational激活函数的PyTorch实现及其特点和优缺点:**

    ```python
    import torch
    import torch.nn as nn

    class Rational(nn.Module):
        def __init__(self, numerator_coeffs, denominator_coeffs):
            super().__init__()
            self.numerator_coeffs = nn.Parameter(numerator_coeffs)
            self.denominator_coeffs = nn.Parameter(denominator_coeffs)

def forward(self, x):
    numerator = torch.polyval(self.numerator_coeffs, x) # 多项式计算
    denominator = 1 + torch.polyval(self.denominator_coeffs, torch.abs(x))  # 绝对值及多项式
    return numerator / denominator

特点: 有理函数（分数函数）形式。分子和分母由多项式表示。
优点: 灵活的函数形态。在某些问题中可能比其他激活函数表现出色。
缺点: 注意分母为0的情况。需要调整超参数（多项式系数）。

基于B样条或傅里叶的激活函数PyTorch实现，特点及优缺点:

B样条激活函数:

import torch
import torch.nn as nn
from scipy.interpolate import BSpline
import numpy as np

class BSplineActivation(nn.Module):
    def __init__(self, knots, degree=3):
        super().__init__()
        self.knots = knots
        self.degree = degree
        self.coeffs = nn.Parameter(torch.randn(len(knots) + degree - 1)) # 控制点

    def forward(self, x):
        # B样条计算
        b = BSpline(self.knots, self.coeffs.detach().numpy(), self.degree) # 分离系数使用
        spline_values = torch.tensor(b(x.detach().numpy()), dtype=torch.float32) # 输入x放入B样条中
        return spline_values * self.coeffs.mean() # 不使用detach, numpy()会报错
         # 不使用detach, numpy()会报错

特点: 局部控制的灵活曲线。通过节点（knot）和次数（degree）调整形态。
优点: 平滑的函数表达。局部特征学习。
缺点: 节点设置会影响性能。计算复杂度增加。

新的激活函数建议及性能评估:

(示例) 结合Swish和GELU的激活函数:

```python
import torch
import torch.nn as nn
import torch.nn.functional as F
class SwiGELU(nn.Module): # Swish + GELU
  def forward(self, x):
    return 0.5 * (x * torch.sigmoid(x) + F.gelu(x))
```

SwiGELU结合了Swish的平滑性和GELU的归一化效果。

实验设计及性能评估: 在FashionMNIST等基准数据集上与现有激活函数进行比较。（实验结果略） ```

参考资料

Deep Learning (Goodfellow, Bengio, Courville, 2016): Chapter 6.3 (Activation Functions) https://www.deeplearningbook.org/
- 包含深度学习全面内容的教科书。除了介绍激活函数的基本知识外，还可以学习深度学习的其他重要概念。
Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010) http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
- 分析了Sigmoid和Tanh激活函数的梯度消失问题，并提出了Xavier初始化方法。对于理解深度神经网络学习的困难非常重要。
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification (He et al., 2015) https://arxiv.org/abs/1502.01852
- 提出了ReLU激活函数、PReLU激活函数以及He初始化方法。可以加深对现代深度学习中广泛使用的ReLU系列激活函数的理解。
Searching for Activation Functions (Ramachandran et al., 2017) https://arxiv.org/abs/1710.05941
- 通过神经网络结构搜索（Neural Architecture Search, NAS）发现了Swish激活函数。可以了解探索新激活函数的方法。
STAF: A Sinusoidal Trainable Activation Function for Deep Learning (Jeon & Cho, 2025) https://arxiv.org/abs/2405.13607 * 最新（2025年）发表在ICLR上的论文，提出了基于傅里叶级数的可学习激活函数STAF。有助于了解适应型激活函数的最新研究趋势。

4 激活函数 (Activation Functions)

4.1 激活函数：向神经网络引入非线性

4.1.1 激活函数的作用：克服线性的局限

4.1.3 激活函数的选择：模型规模、任务和效率

4.2 激活函数的比较

4.2.1 激活函数生成

4.2.2 激活函数的可视化

4.2.3 激活函数对比表

激活函数比较总结

激活函数的数学特性与最新研究趋势

1. 主要激活函数的数学定义、特点及其在深度学习中的作用

2. 损失景观高级分析

3. 局部最小值、鞍点、损失景观：数学分析与最新研究

损失函数地形的几何特性

最新分析技术

鞍点逃离动力学

2023-2024最新研究趋势

实用建议

参考文献

4.3 可视化激活函数对神经网络的影响

4.4 模型训练

4.4.1 单模型训练

4.4.2 根据激活函数进行模型训练

4.5 训练模型的逐层输出和非激活神经元分析

4.5.1 逐层输出分布可视化

4.5.2 非活跃神经元的问题

4.6 确定激活函数候选

计算机视觉 (Computer Vision)

自然语言处理 (NLP)

语音处理 (Speech Processing)

一般建议和最新趋势

深入探讨：设计自己的激活函数 - 理论与实践

1. 激活函数设计的基本原则

2. 创意生成：现有激活函数的组合与变体

3. 数学分析：可微分性、梯度特性

4. PyTorch实现

5. 实验与评估

6. （可选）理论分析

结论

深入探讨：自适应激活函数 - 未来研究方向

1. 自适应激活函数的类型

2. 可能的研究方向

2.1 基于专家混合 (Mixture of Experts, MoE) 的激活函数

2.2 与神经网络结构搜索 (Neural Architecture Search, NAS) 的结合

2.3 物理/生物信息整合

2.4 加强理论分析

3. 结论与建议

练习题

4.2.1 基本问题

4.2.2 应用问题

4.2.3 深化问题

练习题解答

4.2.1 基本问题

4.2.2 应用问题

参考资料