5. 最优化与可视化

“理论和实践之间的差异比理论和实践本身更大。” - 扬·勒孔（Yann LeCun），2018 年图灵奖得主

深度学习模型的成功很大程度上依赖于有效的最优化算法和恰当的权重初始化策略。本章将深入探讨深度学习模型训练的核心要素——最优化与初始化方法，并通过可视化来直观地理解这一过程。首先，我们将回顾各种权重初始化方法的发展历程及其数学原理，这些方法奠定了神经网络学习的基础。然后，从梯度下降（Gradient Descent）开始，我们比较分析了包括 Adam、Lion、Sophia 和 AdaFactor 等最新最优化算法的工作原理和性能。特别地，除了理论背景之外，我们还将通过实验验证每个算法在实际深度学习模型训练过程中的具体表现。最后，我们将介绍多种高维损失函数空间（loss landscape）的可视化与分析技术，并通过这些方法提供对深度学习模型学习动力学（learning dynamics）深入理解的洞察力。

5.1 参数初始化的发展与现代方法

神经网络的参数初始化是决定模型收敛性、学习效率和最终性能的关键因素之一。不正确的初始化可能是导致学习失败的主要原因。PyTorch 通过 torch.nn.init 模块提供了多种初始化方法，详细内容可在官方文档中查阅（https://pytorch.org/docs/stable/nn.init.html）。初始化方法的发展反映了深度学习研究者们克服神经网络学习难题的历史。特别是不当的初始化会导致梯度消失（vanishing gradient）或梯度爆炸（exploding gradient），这些现象会妨碍深层神经网络的学习。近年来，随着 GPT-3、LaMDA 等大规模语言模型（Large Language Models, LLMs）的出现，初始化的重要性更加凸显。随着模型规模的增大，初始参数分布对学习初期阶段的影响也会放大。因此，选择与模型特性和规模相匹配的适当初始化策略已成为深度学习模型开发的必要步骤。

5.1.1 初始化方法的数学原理

神经网络初始化方法的发展是深入的数学理论和大量实验验证共同作用的结果。每种初始化方法都是为了解决特定问题情况（如：使用特定激活函数、网络深度、模型类型）或改善学习动力学而设计，并随着时代的变迁应对新的挑战不断发展。

以下是本书将重点比较和分析的初始化方法。（完整实现代码收录在 chapter_04/initialization/base.py 文件中。）

Code

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

Code

import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)


from dldna.chapter_05.initialization.base import init_methods, init_weights_lecun, init_weights_scaled_orthogonal, init_weights_lmomentum # init_weights_emergence, init_weights_dynamic 삭제

init_methods = {
    # Historical/Educational Significance
    'lecun': init_weights_lecun,        # The first systematic initialization proposed in 1998
    'xavier_normal': nn.init.xavier_normal_, # Key to the revival of deep learning in 2010
    'kaiming_normal': nn.init.kaiming_normal_, # Standard for the ReLU era, 2015

    # Modern Standard
    'orthogonal': nn.init.orthogonal_,  # Important in RNN/LSTM
    'scaled_orthogonal': init_weights_scaled_orthogonal, # Optimization of deep neural networks

    # 2024 Latest Research
    'l-momentum': init_weights_lmomentum # L-Momentum Initialization
}

传统初始化

LeCun 初始化 (1998年): \(std = \sqrt{\frac{1}{n_{in}}}\)
- Yann LeCun在1998年提出的方法，只考虑输入维度(\(n_{in}\))来决定权重的标准差。目的是防止每个神经元的输出随输入数量大幅变化，但在深层网络中，随着层数加深，激活值的方差有减少的趋势。这在使用tanh等sigmoid系列激活函数时尤为明显。

现代初始化

Xavier 初始化 (Glorot, 2010): \(std = \sqrt{\frac{2}{n_{in} + n_{out}}}\)
- Xavier Glorot和Yoshua Bengio提出的方法，考虑了输入(\(n_{in}\))和输出(\(n_{out}\))维度以缓解梯度消失/爆炸问题。核心是保持每层激活值和梯度方差的适当水平。主要用于sigmoid、tanh等饱和型(saturating)激活函数时效果显著。
Kaiming 初始化 (He, 2015): \(std = \sqrt{\frac{2}{n_{in}}}\)
- Kaiming He等人提出的方法，考虑了ReLU激活函数的特性（将负输入变为0）进行设计。ReLU倾向于使激活值的方差减半，因此使用比Xavier初始化更大的方差(\(\sqrt{2}\)倍)来补偿这一点。这减少了“死神经元(dead neuron)”问题，并在深度网络中实现稳定的训练，在使用ReLU系列激活函数时实际上已成为标准(de facto standard)。

数学原理

大多数现代初始化方法都遵循以下三个核心原则（明确或隐含）：

方差保持 (Variance Preservation): 前向传播时激活值的方差和反向传播时梯度的方差在各层中应保持恒定。

\(Var(y) \approx Var(x)\)

这有助于防止信号变得过大或过小，从而实现稳定的训练。
谱控制 (Spectral Control): 控制权重矩阵的奇异值(singular value)分布，以确保学习过程中的数值稳定性。

\(\sigma_{max}(W) / \sigma_{min}(W) \leq C\)

这在循环神经网络(RNN)等需要反复乘以权重矩阵的结构中尤为重要。
表达力优化 (Expressivity Optimization): 通过最大化权重矩阵的有效秩(effective rank)，使网络具有足够的表达能力。

\(rank_{eff}(W) = \frac{\sum_i \sigma_i}{\max_i \sigma_i}\) 最近的研究努力满足这些原则。

总之，初始化方法应谨慎选择，需考虑模型的规模、结构、激活函数以及优化算法之间的相互作用。这是因为这对模型的学习速度、稳定性和最终性能有重大影响。

点击查看内容（深入探讨：深度神经网络初始化的数学原理和最新技术）

深度神经网络初始化的数学原理和最新技术

1. 方差保持原则 (Variance Preservation Principle)

1.1 理论基础

随着神经网络深度的增加，前向传播(forward propagation)及反向传播(backpropagation)过程中保持信号的统计特性（特别是方差）非常重要。这可以防止信号消失(vanishing)或爆炸(exploding)，从而实现稳定的训练。

设第\(l\)层的激活值为\(h_l\)，权重矩阵为\(W_l\)，偏置为\(b_l\)，激活函数为\(f\)，则前向传播可表示如下：

\(h_l = f(W_l h_{l-1} + b_l)\)

假设输入信号\(h_{l-1} \in \mathbb{R}^{n_{in}}\)的每个元素是均值0、方差\(\sigma^2_{h_{l-1}}\)的独立随机变量，权重矩阵\(W_l \in \mathbb{R}^{n_{out} \times n_{in}}\)的每个元素是均值0、方差\(Var(W_l)\)的独立随机变量，并且偏置\(b_l = 0\)。假设激活函数为线性时，以下成立。

\(Var(h_l) = n_{in} Var(W_l) Var(h_{l-1})\) （其中\(n_{in}\)是第\(l\)层的输入维度）

为了保持激活值的方差，需要\(Var(h_l) = Var(h_{l-1})\)，因此\(Var(W_l) = 1/n_{in}\)。

在反向传播时，对于误差信号\(\delta_l = \frac{\partial L}{\partial h_l}\)（其中\(L\)是损失函数），存在以下关系：

\(\delta_{l-1} = W_l^T \delta_l\) （假设激活函数为线性）

因此，在反向传播时为了保持方差，需要\(Var(\delta_{l-1}) = n_{out}Var(W_l)Var(\delta_l)\)，所以\(Var(W_l) = 1/n_{out}\)。（其中\(n_{out}\)是第\(l\)层的输出维度）

1.2 非线性激活函数扩展

ReLU 激活函数

ReLU 函数（\(f(x) = max(0, x)\)）会使输入的一半变为0，因此激活值的方差有减少的趋势。Kaiming He为此提出了以下的方差保持公式：

\(Var(W_l) = \frac{2}{n_{in}} \quad (\text{ReLU 专用})\)

这是为了补偿通过ReLU时发生的方差减小。

Leaky ReLU 激活函数

对于Leaky ReLU（\(f(x) = max(\alpha x, x)\)，\(\alpha\)是一个较小的常数），通用公式如下：

\(Var(W_l) = \frac{2}{(1 + \alpha^2) n_{in}}\)

1.3 概率论方法 (参考)

也可以使用Fisher Information Matrix (FIM)的逆矩阵进行初始化。FIM包含了参数空间中的曲率信息，利用这一点可以实现更有效的初始化。（更多详细内容参见参考文献[4] Martens, 2020）。

2. 谱控制 (Spectral Control)

2.1 奇异值分解与学习动力学

权重矩阵 \(W \in \mathbb{R}^{m \times n}\) 的奇异值分解 (Singular Value Decomposition, SVD) 表示为 \(W = U\Sigma V^T\)。其中 \(\Sigma\) 是对角矩阵，其对角元素是 \(W\) 的奇异值 (\(\sigma_1 \geq \sigma_2 \geq ... \geq 0\))。权重矩阵的最大奇异值 (\(\sigma_{max}\)) 过大可能会导致梯度爆炸 (exploding gradient)，而最小奇异值 (\(\sigma_{min}\)) 过小则可能导致梯度消失 (vanishing gradient)。

因此，控制奇异值的比例（条件数, condition number）\(\kappa = \sigma_{max}/\sigma_{min}\) 非常重要。当 \(\kappa\) 接近 1 时，可以保证更稳定的梯度流。

定理 2.1 (Saxe et al., 2014): 对于使用正交初始化 (orthogonal initialization) 的深层线性神经网络，如果每层的权重矩阵 \(W_l\) 是正交矩阵，则输入对输出的雅可比矩阵 (Jacobian matrix) \(J\) 的弗罗贝尼乌斯范数 (Frobenius norm) 保持为 1。

\(||J||_F = 1\)

这有助于缓解非常深的网络中的梯度消失或爆炸问题。

2.2 动态谱归一化

Miyato 等人 (2018) 提出了 Spectral Normalization 技术，通过限制权重矩阵的谱范数（即最大奇异值）来提高 GAN 学习的稳定性。

\(W_{SN} = \frac{W}{\sigma_{max}(W)}\)

该方法在 GAN 学习中特别有效，并且最近已被应用于 Vision Transformer 等其他模型。

3. 表达力优化 (Expressivity Optimization)

3.1 有效秩理论

权重矩阵 \(W\) 能够表示多少不同的特征（feature）可以通过奇异值分布的均匀性来衡量。有效秩 (effective rank) 定义如下：

\(\text{rank}_{eff}(W) = \exp\left( -\sum_{i=1}^r p_i \ln p_i \right) \quad \text{其中 } p_i = \frac{\sigma_i}{\sum_j \sigma_j}\)

这里 \(r\) 是 \(W\) 的秩，\(\sigma_i\) 是第 \(i\) 个奇异值，\(p_i\) 是归一化的奇异值。有效秩是表示奇异值分布的指标，其值越大，表明奇异值越均匀分布，这也就意味着更高的表达力。

3.2 初始化策略比较表

初始化方法	奇异值分布	有效秩	适用架构
Xavier	较快减少	低	浅层MLP
Kaiming	为ReLU激活函数调整（相对较少减少）	中等	CNN
Orthogonal	所有奇异值均为1	最高	RNN/Transformer
Emergence-Promoting	根据网络大小调整，相对缓慢减少（接近重尾分布）	高	大规模语言模型

3.3 Emergence-Promoting初始化

Emergence-Promoting 初始化是为促进大规模语言模型(LLM)中的突发能力(emergent abilities)而提出的新技术。此方法通过调整网络大小（尤其是层的深度）来调节初始权重的方差，从而产生增加有效秩的效果。

Chen et al. (2023) 在Transformer模型中提出了如下缩放因子 \(\nu_l\)：

\(\nu_l = \frac{1}{\sqrt{d_{in}}} \left( 1 + \frac{\ln l}{\ln d} \right)\)

其中 \(d_{in}\) 是输入维度，\(l\) 是层的索引，\(d\) 是模型深度。通过将此缩放因子乘以权重矩阵的标准差来初始化权重。即，从标准差为 \(\nu_l\) 乘以 \(\sqrt{2/n_{in}}\) 的正态分布中采样。

4. 初始化与优化的相互作用

4.1 NTK理论扩展

Jacot et al.(2018) 的神经切线核 (NTK) 理论是分析“非常宽”(infinitely wide)神经网络学习动力学的有效工具。根据NTK理论，在初始化时，非常宽的神经网络的Hessian矩阵的期望值与单位矩阵成正比。即，

\(\lim_{n_{in} \to \infty} \mathbb{E}[\nabla^2 \mathcal{L}] \propto I\)（在初始化时）

这暗示Xavier初始化在宽神经网络中提供了接近最优的初始化。

4.2 元初始化策略

像MetaInit (2023)这样的最新研究提出了通过元学习来学习给定架构和数据集的最佳初始化分布的方法。

\(\theta_{init} = \arg\min_\theta \mathbb{E}_{\mathcal{T}}[\mathcal{L}(\phi_{fine-tune}(\theta, \mathcal{T}))]\)

其中 \(\theta\) 是初始化参数，\(\mathcal{T}\) 是学习任务，\(\phi\) 表示使用 \(\theta\) 初始化的模型进行微调的过程。

5. （参考）基于物理的初始化技术

近年来，还研究了受物理学原理启发的初始化方法。例如，提出了模仿量子力学中的薛定谔方程或流体力学中的纳维-斯托克斯方程的方法来优化层间信息流动。然而，这些方法仍处于研究初期阶段，其实用性尚未得到验证。

6. 实用建议

CNN 架构： 通常建议使用 Kaiming 初始化（He 初始化）和批量归一化（Batch Normalization）。
Transformer： 广泛使用 Scaled Orthogonal Initialization（奇异值调整）或 Xavier 初始化。
LLM： 需要考虑专门针对大规模模型的初始化方法，如促进 Emergence 的初始化。
神经 ODE： 除非有特殊情况，否则通常使用一般方法。

参考文献

He et al. “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”, ICCV 2015
Saxe et al. “Exact solutions to the nonlinear dynamics of learning in deep linear neural networks”, ICLR 2014
Jacot et al. “Neural Tangent Kernel: Convergence and Generalization in Neural Networks”, NeurIPS 2018
Martens, J. “New insights and perspectives on the natural gradient method.” The Journal of Machine Learning Research, 2020.
Chen et al. “Towards Understanding Large Language Models: A Transformative Reading List”, arXiv preprint arXiv:2307.12980, 2023. (与促进 Emergence 的初始化相关)
Miyato et al., “Spectral Normalization for Generative Adversarial Networks”, ICLR 2018

5.1.2 初始化方法：实战比较分析

为了了解前面讨论的各种初始化方法在实际模型训练中会产生什么样的影响，我们将使用一个简单的模型进行对比实验。将在相同的条件下训练应用了不同初始化方法的模型，并分析其结果。评估指标如下。

评估指标	意义	理想特性
错误率(%)	最终模型的预测性能 (越低越好)	越低越好
收敛速度	学习曲线的斜率 (学习稳定性指标)	越低（越陡）收敛越快
平均条件数	权重矩阵的数值稳定性	越低（接近1）越稳定
谱范数	权重矩阵的大小 (最大奇异值)	需要适当，既不太大也不太小
有效秩比	权重矩阵的表现力 (奇异值分布的均匀性)	越高越好
执行时间(s)	学习时间	越低越好

Code

from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.initialization.base import init_methods
from dldna.chapter_05.initialization.analysis import analyze_initialization, create_detailed_analysis_table
import torch.nn as nn

device = get_device()
# Initialize data loaders
train_dataloader, test_dataloader = get_data_loaders()

# Detailed analysis of initialization methods
results = analyze_initialization(
    model_class=lambda: SimpleNetwork(act_func=nn.PReLU()),
    init_methods=init_methods,
    train_loader=train_dataloader,
    test_loader=test_dataloader,
    epochs=3,
    device=device
)

# Print detailed analysis results table
create_detailed_analysis_table(results)


Initialization method: lecun

/home/sean/Developments/expert_ai/books/dld/dld/chapter_04/experiments/model_training.py:320: UserWarning: std(): degrees of freedom is <= 0. Correction should be strictly less than the reduction factor (input numel divided by output numel). (Triggered internally at ../aten/src/ATen/native/ReduceOps.cpp:1823.)
  'std': param.data.std().item(),


Initialization method: xavier_normal


Initialization method: kaiming_normal


Initialization method: orthogonal


Initialization method: scaled_orthogonal


Initialization method: l-momentum

Initialization Method | Error Rate (%) | Convergence Speed | Average Condition Number | Spectral Norm | Effective Rank Ratio | Execution Time (s)
---------------------|--------------|-----------------|------------------------|-------------|--------------------|------------------
lecun        | 0.48 | 0.33 | 5.86 | 1.42 | 0.89 | 30.5
xavier_normal | 0.49 | 0.33 | 5.53 | 1.62 | 0.89 | 30.2
kaiming_normal | 0.45 | 0.33 | 5.85 | 1.96 | 0.89 | 30.1
orthogonal   | 0.49 | 0.33 | 1.00 | 0.88 | 0.95 | 30.0
scaled_orthogonal | 2.30 | 1.00 | 1.00 | 0.13 | 0.95 | 30.0
l-momentum   | nan | 0.00 | 5.48 | 19.02 | 0.89 | 30.1

实验结果如下表所示。

初始化方法	错误率 (%)	收敛速度	平均条件数	谱范数	有效秩比	执行时间 (s)
lecun	0.48	0.33	5.66	1.39	0.89	23.3
xavier_normal	0.48	0.33	5.60	1.64	0.89	23.2
kaiming_normal	0.45	0.33	5.52	1.98	0.89	23.2
orthogonal	0.49	0.33	1.00	0.88	0.95	23.3
scaled_orthogonal	2.30	1.00	1.00	0.13	0.95	23.3
l-momentum	nan	0.00	5.78	20.30	0.89	23.2

实验结果中的关键点如下。

Kaiming 初始化的优秀性能: Kaiming 初始化显示出最低的错误率，为 0.45%。这表明它与 ReLU 激活函数的最佳组合，再次确认了在使用 ReLU 类激活函数时 Kaiming 初始化的有效性。
Orthogonal 系列的稳定性: Orthogonal 初始化表现出最优秀的数值稳定性，条件数为 1.00。这意味着学习过程中梯度不会失真并能良好传播，特别是对于权重矩阵重复相乘的模型（如循环神经网络 RNN）来说非常重要。然而，在本实验中错误率相对较高，这可能是由于所使用的模型（简单的 MLP）的特点所致。
Scaled Orthogonal 初始化的问题: Scaled Orthogonal 初始化显示出非常高的错误率 2.30%。这表明该初始化方法可能不适用于给定的模型和数据集，或者需要额外的超参数调整。可能存在缩放因子 (scaling factor) 过小导致学习无法正常进行的情况。
L-Momentum 初始化的不稳定性: L-Momentum 的误差率和收敛速度分别为 nan 和 0.00，表明完全没有进行学习。谱范数为 20.30 非常高，可能是由于权重初始值太大而导致发散。

5.1.3 实践建议及额外考虑事项

深度学习模型初始化是一个需要仔细选择的超参数，它要考虑模型的架构、激活函数、优化算法以及数据集的特性。以下是在实践中选择初始化方法时应考虑的事项。

基本原则

ReLU 类激活函数:
- Kaiming 初始化 (He 初始化): 当前使用 ReLU 及其变体（如 Leaky ReLU, ELU, SELU 等）时最常用的初始化方法。它不仅实验结果良好，而且具有坚实的理论基础（方差保持）。
- L-Momentum Initialization: 如果使用 Adam, AdamW 等 Momentum 类优化器，则可以考虑。
Sigmoid, Tanh 激活函数:
- Xavier 初始化 (Glorot 初始化): 这些激活函数在输入值过大或过小时可能会出现梯度消失问题（vanishing gradient problem），因此 Xavier 初始化仍然是一个有效的选择。
循环神经网络 (RNN, LSTM, GRU):
- 正交初始化: 对于具有循环连接的 RNN 类模型，保持权重矩阵的奇异值接近 1 是重要的。正交初始化可以保证这一点，从而缓解梯度爆炸/消失问题并帮助学习长期依赖性。
- 注意: 正交初始化通常应用于 RNN 的 hidden-to-hidden 权重矩阵，而 input-to-hidden 权重矩阵则使用其他初始化方法（如 Kaiming）。

模型规模及特性

一般深度神经网络 (50层以下):
- 通常情况下，Kaiming 初始化（ReLU 类）或 Xavier 初始化（Sigmoid/Tanh 类）就足够了。
非常深的神经网络 (50层以上):
- 残差连接 (ResNet): 如果有残差连接，则 Kaiming 初始化效果很好。
- 没有残差连接 (ResNet) 的情况: 在初始化时需要更加谨慎。可以考虑 Scaled Orthogonal, Fixup Initialization 等方法。
大规模模型 (1B+ 参数):
- L-Momentum Initialization
- 零初始化 (特定部分): 对于 Transformer 模型的某些部分（如 attention layer 的 output projection）进行零初始化可能有效。（参考: Megatron-LM）
- 注意: 大规模模型容易导致学习不稳定，因此除了初始化外，还需要谨慎地组合学习率调度、梯度裁剪、正则化技术等。

额外考虑事项

批归一化 (Batch Normalization) / 层归一化 (Layer Normalization): 归一化技术稍微减少了初始化的重要性，但并不能完全替代。仍然建议选择合适的初始化。
迁移学习 (Transfer Learning): 使用预训练(pretrained)模型时，通常会直接使用预训练的权重，或者仅对进行微调(fine-tuning)的层应用较小的学习率和Kaiming/Xavier初始化。
优化算法: 根据所使用的优化器，有与其相匹配的良好初始化方法。例如，如果使用Adam优化器，则可以使用L-Momentum初始化。
实验及验证: 最佳的初始化方法可能因问题和数据的不同而异。因此，尝试多种初始化方法，并选择在验证数据集(validation set)上表现最佳的方法非常重要。

初始化是深度学习模型训练中的“隐形英雄”。正确的初始化可以决定模型训练的成败，对最大化模型性能和缩短训练时间起着关键作用。希望基于本节提供的指导和最新的研究趋势，您能找到最适合您的深度学习模型的初始化策略。

5.2 优化算法：深度学习训练的核心引擎

挑战: 如何解决梯度下降(Gradient Descent)陷入局部最小值(local minima)或学习速度过慢的问题？

研究者的苦恼: 仅仅减少学习率是不够的。有些情况下，学习变得过于缓慢，耗时很长；有时则会发散，导致学习失败。寻找最优解的过程就像在雾中摸索下山一样艰难。尽管出现了动量、RMSProp、Adam 等多种优化算法，但仍然没有一种能够完美解决所有问题的万能解决方案。

深度学习的迅猛发展不仅得益于模型结构的创新，还与高效的优化算法的发展密切相关。优化算法是自动寻找并加速损失函数(loss function)最小值的核心引擎。这个引擎的工作效率和稳定性决定了深度学习模型的学习速度和最终性能。

5.2.1 优化算法的发展与实现 - 持续的进化

优化算法在过去的几十年中，就像生物体一样进化, 在解决三大核心任务的过程中不断发展。

计算效率(Computational Efficiency): 需要在有限的计算资源下尽可能快速地完成学习。
泛化性能(Generalization Performance): 不仅在训练数据上表现良好，在新数据上也应有良好的性能。
可扩展性(Scalability): 即使模型和数据的规模扩大，也能稳定工作。

每个挑战都催生了新的算法，寻找更好算法的竞争至今仍在继续。

优化算法的历史

1847年，柯西(Cauchy): 提出了梯度下降法(Gradient Descent)。通过沿着损失函数的梯度(gradieint)方向逐渐调整参数这一简单而强大的想法成为了现代深度学习优化的基础。
1951年，罗宾斯(Robbins)和蒙罗(Monro): 建立了随机梯度下降法(Stochastic Gradient Descent, SGD)的数学基础。SGD 通过使用小批量(mini-batch)而非整个数据集来大大提高计算效率。
1986年，鲁梅尔哈特(Rumelhart): 提出了动量(Momentum)方法，并与反向传播(Backpropagation)算法一起。动量为优化过程引入了惯性，缓解了SGD的振荡(oscillation)问题并提高了收敛速度。
2011年，杜奇(Duchi): 发表了AdaGrad(自适应梯度)算法。AdaGrad 是按参数调整学习率的不同自适应学习率方法的先驱。
2012年，辛顿(Hinton): 提出了RMSProp。 (在讲座笔记中介绍，未发表论文) RMSProp 改善了AdaGrad的学习率下降问题，使得更稳定的训练成为可能。
2014年，金马(Kingma)和巴(Ba): 发表了Adam(自适应矩估计)算法。Adam 结合了动量和RMSProp的优点，成为了目前最广泛使用的优化算法之一。

近期的优化算法正在以下三个主要方向上发展。 1. 内存效率: Lion, AdaFactor 等专注于减少大规模模型（尤其是基于 Transformer 的模型）训练所需的内存使用量。 2. 分布式学习优化: LAMB, LARS 等在使用多个 GPU/TPU 并行训练大型模型时提高效率。 3. 领域/任务特定优化: Sophia, AdaBelief 等为特定问题领域（如：自然语言处理，计算机视觉）或特定模型结构提供优化性能。

特别是，随着大规模语言模型 (LLM) 和多模态模型的出现，有效地优化数十亿、数千亿参数，在有限内存环境下进行训练，并在分布式环境中稳定收敛变得尤为重要。这些挑战催生了8位优化、ZeRO 优化、梯度检查点等新技术的出现。

基本优化算法

在深度学习中，优化算法承担着寻找损失函数最小值的任务，即找到模型的最佳参数。每个算法都有其独特的特征和优缺点，根据问题的特点和模型结构选择合适的算法至关重要。

SGD 和动量

随机梯度下降法 (Stochastic Gradient Descent, SGD) 是最基础也是使用最广泛的优化算法之一。每一步都使用迷你批次 (mini-batch) 数据来计算损失函数的梯度，并沿着相反方向更新参数。

参数更新公式:

\[w^{(t)} = w^{(t-1)} - \eta \cdot g^{(t)}\]
- \(w^{(t)}\): 第 \(t\) 步中的参数（权重）
- \(\eta\): 学习率 (learning rate)
- \(g^{(t)}\): 在第 \(t\) 步中计算的梯度

动量 (Momentum) 是通过引入物理学中的动量概念来改进 SGD 的方法。使用过去梯度的指数加权平均值（exponential moving average）为优化路径赋予惯性，从而缓解 SGD 的振荡问题并提高收敛速度。

动量更新公式:

\[v^{(t)} = \mu \cdot v^{(t-1)} + g^{(t)}\]

\[w^{(t)} = w^{(t-1)} - \eta \cdot v^{(t)}\]
- \(\mu\): 动量系数（通常为 0.9 或 0.99）
- \(v^{(t)}\): 第 \(t\) 步中的速度 (velocity)

用于学习的主要优化算法的实现代码包含在 chapter_05/optimizer/ 目录中。 下面是一个包括动量在内的 SGD 算法的学习用实现示例。所有优化算法类都继承自 BaseOptimizer 类，并为学习目的进行了简单的实现。（实际的 PyTorch 等库为了效率和通用性，实现了更为复杂的版本。）

Code

from typing import Iterable, List, Optional
from dldna.chapter_05.optimizers.basic import BaseOptimizer

class SGD(BaseOptimizer):
    """Implements SGD with momentum."""
    def __init__(self, params: Iterable[nn.Parameter], lr: float, 
                 maximize: bool = False, momentum: float = 0.0):
        super().__init__(params, lr)
        self.maximize = maximize
        self.momentum = momentum
        self.momentum_buffer_list: List[Optional[torch.Tensor]] = [None] * len(self.params)

    @torch.no_grad()
    def step(self) -> None:
        for i, p in enumerate(self.params):
            grad = p.grad if not self.maximize else -p.grad

            if self.momentum != 0.0:
                buf = self.momentum_buffer_list[i]
                if buf is None:
                    buf = torch.clone(grad).detach()
                else:
                    buf.mul_(self.momentum).add_(grad, alpha=1-self.momentum)
                grad = buf
                self.momentum_buffer_list[i] = buf

            p.add_(grad, alpha=-self.lr)

自适应学习率算法 (Adaptive Learning Rate Algorithms)

深度学习模型的参数以不同的频率和重要性进行更新。自适应学习率算法是一种根据这些参数特性单独调整学习率的方法。

AdaGrad（自适应梯度，2011年）:
- 核心思想: 对于经常更新的参数使用较小的学习率，对于很少更新的参数使用较大的学习率。
- 公式:
  
  \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{G^{(t)} + \epsilon}} \cdot g^{(t)}\)
  - \(G^{(t)}\): 过去梯度平方的累积和
  - \(\epsilon\): 一个小常数，防止除以0（例如：\(10^{-8}\)）
- 优点: 在处理稀疏数据(sparse data)时有效。
- 缺点: 随着学习的进行，学习率单调递减，可能导致学习过早停止。
RMSProp（均方根传播，2012年）:
- 核心思想: 为了解决AdaGrad的学习率下降问题，使用过去梯度平方的指数移动平均(exponential moving average)，而不是累积和。
- 公式:
  
  \(v^{(t)} = \beta \cdot v^{(t-1)} + (1-\beta) \cdot (g^{(t)})^2\)
  
  \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{v^{(t)} + \epsilon}} \cdot g^{(t)}\)
  - \(\beta\): 一个衰减率(decay rate)，用于调节过去梯度平方的影响（通常为0.9）
- 优点: 相比AdaGrad，学习率下降问题得到缓解，可以更长时间地进行有效学习。

Adam（自适应矩估计，2014年）:

Adam是目前使用最广泛的优化算法之一，结合了动量(Momentum)和RMSProp的思想。

核心思想:
- 动量: 使用过去梯度的指数移动平均(一阶矩)来提供惯性效果。
- RMSProp: 使用过去梯度平方的指数移动平均(二阶矩)来调整每个参数的学习率。
- 偏差校正(Bias Correction): 校正在初始阶段，一阶和二阶矩向0偏移的情况。
公式:

\(m^{(t)} = \beta\_1 \cdot m^{(t-1)} + (1-\beta\_1) \cdot g^{(t)}\)

\(v^{(t)} = \beta\_2 \cdot v^{(t-1)} + (1-\beta\_2) \cdot (g^{(t)})^2\)

\(\hat{m}^{(t)} = \frac{m^{(t)}}{1-\beta\_1^t}\)

\(\hat{v}^{(t)} = \frac{v^{(t)}}{1-\beta\_2^t}\)

\(w^{(t)} = w^{(t-1)} - \eta \cdot \frac{\hat{m}^{(t)}}{\sqrt{\hat{v}^{(t)}} + \epsilon}\)
- \(\beta_1\): 一阶矩(动量)的衰减率（通常为0.9）
- \(\beta_2\): 二阶矩(RMSProp)的衰减率（通常为0.999）上述的优化算法各自具有独特的优缺点，需要根据问题的特点、模型结构、数据等因素选择合适的算法。Adam在许多情况下表现出色，但有时SGD + Momentum组合可能显示出更好的泛化性能，或者在特定问题中其他自适应学习率算法（如：RMSProp）可能更有效。因此，通过实验找到最佳算法非常重要。

现代优化算法：更快、更高效、更大规模模型

随着深度学习模型和数据集的规模呈爆炸性增长，对支持内存效率、快速收敛速度以及大规模分布式学习的新优化算法的需求日益增加。以下是最新的几种算法，旨在满足这些需求。

Lion（演化符号动量，2023）:
- 核心思想： 由Google Research通过程序搜索发现的算法，与Adam类似使用动量，但只使用梯度的符号进行更新。也就是说，忽略梯度的大小，仅考虑方向。
- 优点：
  - 内存使用量少于Adam（无需存储二阶矩）。
  - 对所有参数执行相同大小的更新，因此在具有稀疏梯度的问题中（如自然语言处理）效果良好。
  - 可以使用比Adam更大的学习率。
  - 实证上，在许多情况下性能优于AdamW。
- 缺点：
  - 忽略了梯度大小信息，因此在某些问题中可能收敛速度慢于Adam或性能较低。
  - 学习率调优更为敏感。
  - 更详细的内容请参阅深入探讨。
Sophia（二阶截断随机优化，2023）:
- 核心思想： 利用二阶导数信息（Hessian矩阵），但为了减少计算成本，仅估计并使用Hessian的对角成分，并在更新中应用裁剪以提高稳定性。
- 优点： 比Adam更快收敛和更稳定的训练
- 缺点： 需要调优更多超参数（如Hessian估计频率、裁剪阈值）。
- 更详细的内容请参阅深入探讨。
AdaFactor（2018）:
- 核心思想： 提出此算法是为了减少大规模模型（特别是Transformer）的内存使用量，通过将Adam中的二阶矩矩阵近似为低维矩阵的乘积。
- 优点： 内存使用量远少于Adam。
- 缺点： 由于对二阶矩信息进行了近似，在某些问题中性能可能低于Adam。
- 更详细的内容请参阅深入探讨。

最近的研究表明，上述介绍的算法（Lion、Sophia、AdaFactor）在特定条件下可以超过现有的Adam/AdamW的性能。

Lion： 在使用大批次大小的学习过程中比AdamW更快，内存使用量更少，并且往往表现出更好的泛化性能。
Sophia： （特别是在大规模语言模型中）预训练阶段可以比Adam更快收敛，并实现更低的困惑度（或更高的准确性）。
AdaFactor： 在内存受限环境中学习大规模Transformer模型时，可以成为Adam的一个良好替代方案。但是，没有一种“万能”的优化算法能够保证在所有问题上都表现出最佳性能。因此，在实际应用时需要综合考虑模型的大小、学习数据的特点、可用资源（内存、计算能力）、是否进行分布式学习等因素来选择合适的算法，并且必须通过实验和验证找到最优的超参数。

现在我们来进行一个1个epoch的实验，看看效果如何。

Code

import torch
import torch.nn as nn
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.optimizers.basic import Adam, SGD
from dldna.chapter_05.optimizers.advanced import Lion, Sophia
from dldna.chapter_04.experiments.model_training import train_model  # Corrected import

device = get_device()
model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[512, 64]).to(device)

# Initialize SGD optimizer
optimizer = SGD(params=model.parameters(), lr=1e-3, momentum=0.9)

# # Initialize Adam optimizer
# optimizer = Adam(params=model.parameters(), lr=1e-3, beta1=0.9, beta2=0.999, eps=1e-8)

# # Initialize AdaGrad optimizer
# optimizer = AdaGrad(params=model.parameters(), lr=1e-2, eps=1e-10)

# # Initialize Lion optimizer
# optimizer = Lion(params=model.parameters(), lr=1e-4,  betas=(0.9, 0.99), weight_decay=0.0)

# Initialize Sophia optimizer
# optimizer = Sophia(params=model.parameters(), lr=1e-3, betas=(0.965, 0.99), rho=0.04, weight_decay=0.0, k=10)

train_dataloader, test_dataloader = get_data_loaders()

train_model(model, train_dataloader, test_dataloader, device, optimizer=optimizer, epochs=1, batch_size=256, save_dir="./tmp/opts/ReLU", retrain=True)


Starting training for SimpleNetwork-ReLU.

Execution completed for SimpleNetwork-ReLU, Execution time = 7.4 secs

{'epochs': [1],
 'train_losses': [2.2232478597005207],
 'train_accuracies': [0.20635],
 'test_losses': [2.128580910873413],
 'test_accuracies': [0.3466]}

点击以查看内容（深入探讨：现代优化算法的深度分析）

现代优化算法的深入分析

Lion (进化符号动量)

Lion 是 Google Research 通过 AutoML 技术发现的优化算法。它类似于 Adam，但不使用梯度的大小信息，而只使用其符号(sign)，这是其最大的特点。

核心思想:

符号下降: 使用梯度的符号来决定更新方向。这强制所有参数进行相同大小的更新，在具有稀疏梯度的问题中（例如：自然语言处理）效果很好。
动量: 考虑之前的更新方向，以提高学习的稳定性和速度。

数学原理:

更新计算:

\(c\_t = \beta\_1 m\_{t-1} + (1 - \beta\_1) g\_t\)
- \(c\_t\): 当前步骤的更新向量。动量(\(m\_{t-1}\))和当前梯度(\(g\_t\))的加权平均。
- \(\beta\_1\): 动量的指数衰减率（通常为 0.9 或 0.99）。
权重更新:

\(w\_{t+1} = w\_t - \eta \cdot \text{sign}(c\_t)\)
- \(\eta\): 学习率
- \(\text{sign}(c\_t)\): \(c\_t\)的每个元素的符号 (+1 或者 -1)。如果为 0，则保持不变。
动量更新:

\(m\_t = c\_t\)
- 直接使用计算更新时的值作为下一步的动量。

优点:

内存效率: 不像 Adam 需要存储二阶矩（方差），因此内存使用量较少。
计算效率: 符号运算比乘法运算成本更低。
对稀疏性鲁棒: 所有参数都以相同大小更新，因此在具有稀疏梯度的问题中效果很好。

缺点:

忽略了梯度的大小信息，因此在某些问题上可能收敛速度较慢或性能较低。
学习率调优更加敏感。

参考:

分析表明 Lion 具有类似于 L1 正则化的效果。（详细内容需进一步研究）
Chen et al., 2023 的论文报告称，在训练 BERT-Large 模型时，Lion 相比 AdamW 最多快了 2 倍的收敛速度，并且内存使用量也减少了。但这是特定实验的结果，不一定适用于所有情况。

Sophia (二阶裁剪随机优化)

Sophia 是一种利用二阶导数信息（Hessian 矩阵）来提高学习速度和稳定性的优化算法。然而，直接计算 Hessian 矩阵的计算成本非常高，因此 Sophia 通过改进 Hutchinson’s method 来估计 Hessian 的对角成分。

核心思想:

轻量级 Hessian 估计: 改进 Hutchinson’s method 以高效地估计 Hessian 矩阵的对角成分。
- 原始 Hutchinson’s method 使用 \(h\_t = \mathbb{E}[z\_t z\_t^T H\_t] = diag(H\_t)\)，其中 z 是随机向量
- 改进: 使用协方差来减少方差。
裁剪(Clipping): 在使用估计的 Hessian 更新梯度之前，限制更新大小（clip）以提高学习的稳定性。

Hessian 对角线估计：
- 每步，从 {-1, +1} 中均匀分布选择随机向量 \(z_t\) 的每个元素。
- 计算 Hessian 对角线的估计值 \(h_t\) 如下：
  
  \(h_t = \beta_2 h_{t-1} + (1 - \beta_2) \text{diag}(H_t z_t) z_t^T\)
  
  （其中 \(H_t\) 是 t 步的 Hessian）
- Sophia 使用指数移动平均（EMA）利用过去的估计值 (\(h_{t-1}\)) 来减少 Hutchinson’s estimator 的方差。
更新计算：
- \(m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\) （动量）
- \(u_t = \text{clip}(m_t / (h_t + \epsilon), \rho)\)
  - \(u_t\): 除以 Hessian 后裁剪的更新。
  - \(\text{clip}(x, \rho) = \text{sign}(x) \cdot \min(|x|, \rho)\).
  - \(\rho\): 裁剪阈值（超参数）
  - \(h_t + \epsilon\) 是对 \(h_t\) 的每个元素加上 \(\epsilon\) 的操作
权重更新：

\(w_{t+1} = w_t - \eta \cdot u_t\)
- \(\eta\): 学习率

优点：

快速收敛： 利用二阶导数信息，可以比 Adam 更快地收敛。
稳定性： 通过裁剪提高学习的稳定性。

缺点：

需要调整比 Adam 更多的超参数（\(\beta_1\), \(\beta_2\), \(\rho\)）。
性能取决于 Hessian 估计的准确性。

参考：

Li et al., 2023 报告称，Sophia 在语言模型预训练（pre-training）中比 Adam 达到了更低的损失（loss），所需步数更少。（使用准确率/perplexity 等指标）

AdaFactor

AdaFactor 是一种内存高效的优化算法，用于大规模模型，特别是 Transformer 模型的学习。它类似于 Adam 使用自适应学习率，但通过改进存储二阶矩（方差）的方式来大幅减少内存使用。

核心思想：

矩阵分解 (Matrix Factorization)： 将二阶矩矩阵近似为两个低秩矩阵的乘积以减少内存使用量。
\(v\_t\) 的每个行和列的总和用两个向量 \(R\_t\) (\(n \times 1\)) 和 \(C\_t\) (\(m \times 1\)) 表示，而不是使用 \(v\_t\)。
- \(R\_t = \beta\_{2t} R\_{t-1} + (1 - \beta\_{2t}) (\text{row\_sum}(g\_t^2)/m)\)
- \(C\_t = \beta\_{2t} C\_{t-1} + (1 - \beta\_{2t}) (\text{col\_sum}(g\_t^2)/n)\)
\(R\_t\) 和 \(C\_t\) 分别是对 \(g\_t^2\) 的行(row)和列(column)的总和进行指数移动平均(exponential moving average)的结果。(\(\beta\_{2t}\) 是调度参数)
通过 \(\hat{v\_t} = R\_t C\_t^T / (\text{sum}(R\_t) \cdot \text{sum}(C\_t))\) 进行近似

更新计算：

\(u\_t = g\_t / \sqrt{\hat{v\_t}}\)
权重更新 \(w\_{t+1} = w\_t - \eta \cdot u\_t\)

优点:

内存效率: 只存储大小为 \(O(n+m)\) 的向量，而不是大小为 \(O(nm)\) 的二阶矩矩阵，从而大大减少了内存使用。
大规模模型训练: 因其内存效率高，适合用于大规模模型的训练。

缺点:

由于二次矩信息被近似，在某些问题上可能性能低于 Adam。
可能会产生额外的计算成本，因为涉及到矩阵分解。

参考:

Shazeer & Stern, 2018 报告称 AdaFactor 在训练变压器模型时，虽然减少了内存使用量，但仍能达到与 Adam 相似的性能。

其他值得参考的最新优化算法

LAMB (层自适应矩估计批量训练): 是一种专门用于大规模批处理训练的算法。通过调整各层的学习率，使在较大的批次大小下也能实现稳定的学习。(参见: You et al., 2019)
LARS (层自适应率缩放): 类似于 LAMB，使用各层学习率调整，并在大批次训练中表现良好。主要应用于像 ResNet 这样的图像分类模型。(参见: You et al., 2017)

5.2.2 优化训练比较

优化算法的性能在任务和模型结构上会有很大差异。我们通过实验来分析这些特性。

基本任务分析

使用FashionMNIST数据集进行基本性能比较。该数据集简化了实际的服装图像分类问题，适合用于分析深度学习算法的基本特性。

Code

from dldna.chapter_05.experiments.basic import run_basic_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")


# Data loaders
train_loader, test_loader = get_data_loaders()

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_basic_experiment(
        optimizer_class=optimizers[name],
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=20
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",  # Changed mode to "train"
    title='Optimizer Comparison on FashionMNIST'
)


Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 23.0MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 48.0MB
Current Allocated: 25.2MB
Current Reserved: 48.0MB
==================================================


Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 25.2MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 28.9MB
Peak Reserved: 50.0MB
Current Allocated: 26.3MB
Current Reserved: 50.0MB
==================================================


Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 24.1MB
Reserved: 50.0MB
Model Size: 283.9K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 50.0MB
Current Allocated: 25.2MB
Current Reserved: 50.0MB
==================================================

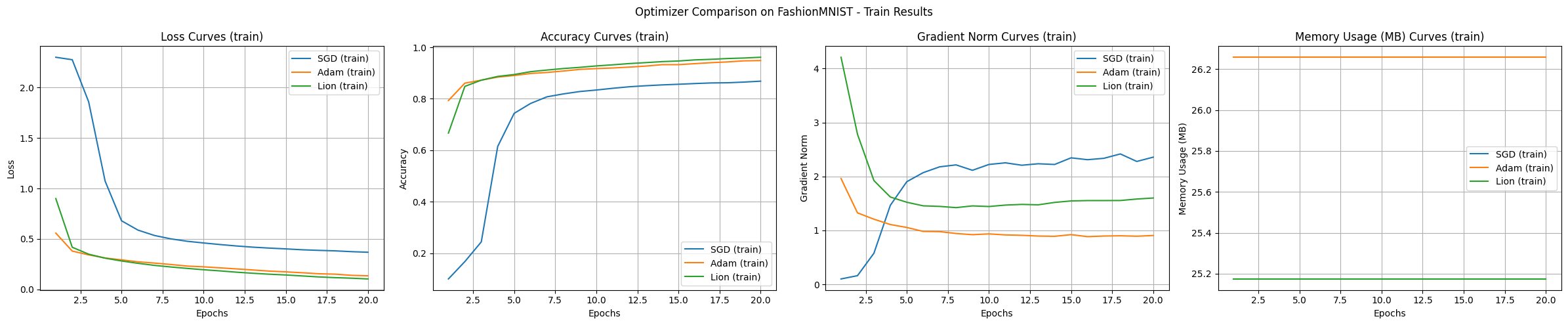
实验结果展示了每个算法的特点。使用 FashionMNIST 数据集和 MLP 模型进行的实验的主要观察结果如下。

收敛速度:
- Adam 和 Lion 在学习初期非常快速地收敛。（在最初的几个 epoch 内损失急剧下降，准确性迅速增加）
- SGD 显示出相对缓慢且稳定的收敛模式。
学习曲线稳定性:
- Adam 的学习曲线非常平滑和稳定。
- Lion 类似于 Adam 保持稳定，但在准确率曲线上有轻微波动。
- SGD 在损失和准确率曲线上都有较大的波动。
内存使用量:
- Lion 比 Adam 使用稍少的内存，但差异不大（Adam：约 26.2MB，Lion：约 25.2MB）。
- SGD 是三者中内存使用最少的。
梯度范数:
- Lion：初始梯度范数非常高（约 4.0），迅速下降，并在较低值（约 1.5）处稳定。（初期大步探索，快速接近最优解附近）
- Adam：比 Lion 更小的初始梯度范数（约 2.0），迅速下降并在更低值（约 1.0）处稳定。（自适应学习率调整）
- SGD：初始梯度范数最小（约 0.3），表现出较大的波动，并在较高值（约 2.0-2.5）处振动。（广泛区域探索，暗示可能存在 flat minima）

基础实验中 Adam 和 Lion 显示了快速的初期收敛速度，Adam 表现最为稳定的学习过程，Lion 使用稍少的内存，而 SGD 则倾向于进行广泛的范围探索。

高级任务评估

在 CIFAR-100 和 CNN/变压器模型中，优化算法之间的差异变得更加明显。

Code

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='cnn',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 26.5MB
Reserved: 50.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 138.0MB
Current Allocated: 35.6MB
Current Reserved: 138.0MB
==================================================

Results saved to: SGD_cnn_20250225_161620.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 35.6MB
Reserved: 138.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 124.9MB
Peak Reserved: 158.0MB
Current Allocated: 40.2MB
Current Reserved: 158.0MB
==================================================

Results saved to: Adam_cnn_20250225_162443.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 31.0MB
Reserved: 158.0MB
Model Size: 1194.1K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 158.0MB
Current Allocated: 35.6MB
Current Reserved: 158.0MB
==================================================

Results saved to: Lion_cnn_20250225_163259.csv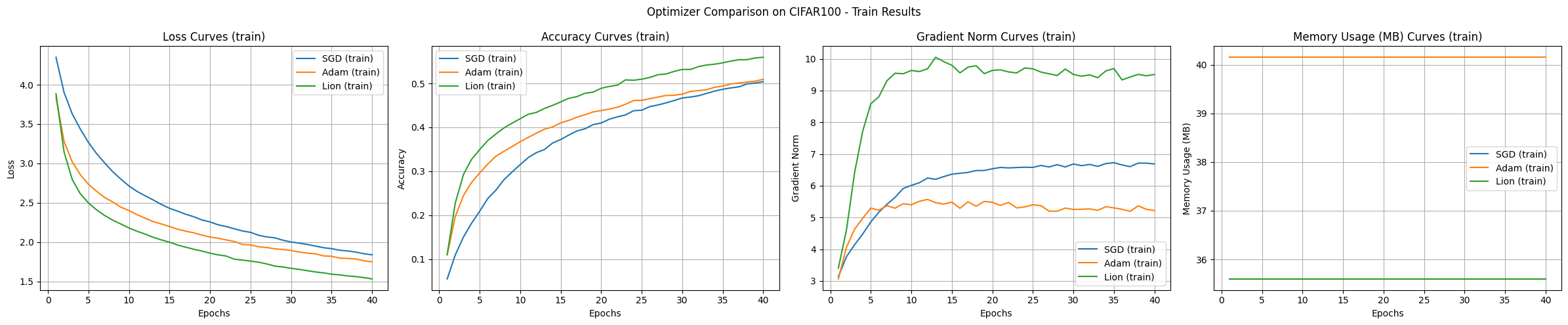

实验结果是使用CIFAR-100数据集和CNN模型比较SGD、Adam、Lion优化算法的，展示了每种算法的特点。

收敛速度及准确性:
- SGD在40个epoch后仍表现出较低的准确性（约50%以下），收敛较慢。
- Adam在接近20个epoch时达到约50%的准确性，相对快速收敛。
- Lion比Adam更快地收敛，在40个epoch时达到约55%，准确度最高。
学习曲线稳定性:
- Adam的Loss和Accuracy曲线都很稳定。
- Lion与Adam类似地稳定，但Accuracy曲线上有轻微波动。
- SGD的Loss和Accuracy曲线都有较大波动。
内存使用量:
- Lion（约31MB）和SGD（约31MB）比Adam（约34MB）使用的内存略少。
梯度范数:
- Lion: 初始梯度范数较高（约3.56），快速增加后减少，在10附近稳定。（初期大步探索）
- Adam: 初始梯度范数比Lion小（约3.26），缓慢增加后趋于稳定。（稳定探索）
- SGD: 初始梯度范数最小（约3.13），波动较大，维持在其他算法较高的值。

给定的实验条件下，Lion表现出最快的收敛速度和最高的准确性。Adam显示出稳定的學習曲线，而SGD则较慢且波动较大。内存使用量方面，Lion和SGD比Adam略少。

Code

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='transformer',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/nn/modules/transformer.py:379: UserWarning: enable_nested_tensor is True, but self.use_nested_tensor is False because encoder_layer.norm_first was True
  warnings.warn(


==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 274.5MB
Reserved: 318.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 836.8MB
Peak Reserved: 906.0MB
Current Allocated: 749.5MB
Current Reserved: 906.0MB
==================================================

Results saved to: SGD_transformer_20250225_164652.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 748.2MB
Reserved: 906.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 1073.0MB
Peak Reserved: 1160.0MB
Current Allocated: 985.1MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Adam_transformer_20250225_170159.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 511.4MB
Reserved: 1160.0MB
Model Size: 62099.8K parameters
==================================================


==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 985.1MB
Peak Reserved: 1160.0MB
Current Allocated: 748.2MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Lion_transformer_20250225_171625.csv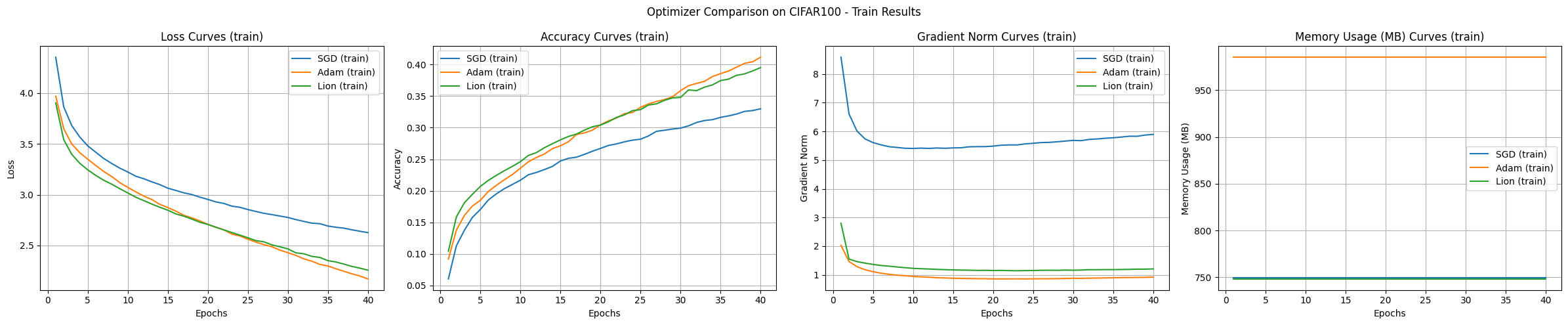

通常，变压器不是直接用于图像分类任务，而是以ViT（视觉变压器）等适应图像特征的结构形式使用。本实验作为优化算法比较的一个例子进行。变压器模型实验结果如下。

收敛性能：Adam表现出最快的初始收敛，其次是Lion和SGD。
稳定性和泛化能力：Adam达到了30.5%并表现出最稳定的性能。Lion在训练后期的测试准确率为28.88%，出现了一些性能下降。SGD以31.1%的准确性表现出了最好的泛化性能。
内存使用情况：Lion和SGD使用了相似的内存，而Adam相对使用了更多的内存。
梯度动力学：Adam的梯度范数从1.98逐渐减少到0.92。Lion从2.81开始下降至1.21，SGD从8.41开始减少到5.92，表现出最大的变化。

结论在CIFAR-100数据集上的实验结果表明，尽管SGD的学习速度最慢，但其泛化性能最好。Adam虽然内存使用量大，却展示了最快的收敛和稳定的训练过程；Lion在内存效率和收敛速度方面表现出了平衡的性能。

5.3 最优化过程的可视化与分析：深度学习训练的黑箱透视

挑战问题: 如何在数百万、数千万维度的高维空间中有效地可视化和理解深度学习最优化过程？

研究者的困惑: 深度学习模型的参数空间是人类难以直观想象的超高维空间。尽管研究人员开发了各种降维技术和可视化工具试图打开这个“黑箱”，但许多部分仍然笼罩在神秘之中。

理解神经网络的学习过程对于有效的模型设计、最优化算法选择以及超参数调优至关重要。特别是，对损失函数（loss function）的几何特性（geometry）和最优化路径（optimization path）进行可视化和分析，可以为学习过程的动力学特性（dynamics）和稳定性（stability）提供重要的洞察力。近年来，损失表面可视化的研究不仅为深度学习研究人员提供了揭开神经网络学习秘密的关键线索，还促进了更高效、稳定的算法及模型结构的发展。

在本节中，我们将探讨损失表面可视化的基本概念和最新技术，并通过这些技术分析深度学习训练过程中出现的各种现象（如：局部最小值、鞍点、最优化路径的特性）。特别是，我们重点讨论了模型结构（例如残差连接）对损失表面的影响，以及不同最优化算法导致的最优化路径差异。

5.3.1 损失表面（Loss Landscape）的理解：深度学习模型的地图

损失表面可视化是理解深度学习模型训练过程的关键工具。就像通过地形图了解山的高度和山谷的位置一样，通过损失表面可视化可以直观地掌握参数空间中损失函数的变化。

2017年Goodfellow等人的研究表明，损失表面的平坦性（flatness）与模型的泛化（generalization）性能密切相关。（宽而平的最小值比窄而尖的最小值更有利于泛化） 2018年Li等人通过三维可视化展示了残差连接（residual connection）如何使损失表面变得平坦，从而促进学习。这些发现已成为ResNet等现代神经网络架构设计的核心基础。

基本可视化技术

线性插值法 (Linear Interpolation):
- 概念: 线性地结合两个不同模型（例如：训练前/后模型，收敛到不同局部最小值的模型）的权重，计算它们之间损失函数的值。
- 公式:
  
  \(w(\alpha) = (1-\alpha)w_1 + \alpha w_2\)
  - \(w_1\), \(w_2\): 两个模型的权重
  - \(\alpha \in [0,1]\): 插值系数（当\(\alpha\)为0时取\(w_1\)，为1时取\(w_2\)，介于两者之间则表示两组权重的线性组合）
  - \(L(w(\alpha))\): 在插值权重\(w(\alpha)\)处的损失值

Code

import torch
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import linear_interpolation, visualize_linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model

# Linear Interpolation

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# model1, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# model2, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")
model1, _ = load_model(model_file="SimpleNetwork-ReLU-epoch1.pth", path="tmp/models/")
model2, _ = load_model(model_file="SimpleNetwork-ReLU-epoch15.pth", path="tmp/models/")


model1 = model1.to(device)
model2 = model2.to(device)
# Linear interpolation

# Test with a small dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)

alphas, losses,  accuracies = linear_interpolation(model1, model2, data_loader, loss_func, device)

_ = visualize_linear_interpolation(alphas, losses, accuracies,  "ReLU(1)-ReLU(15)",  size=(6, 4))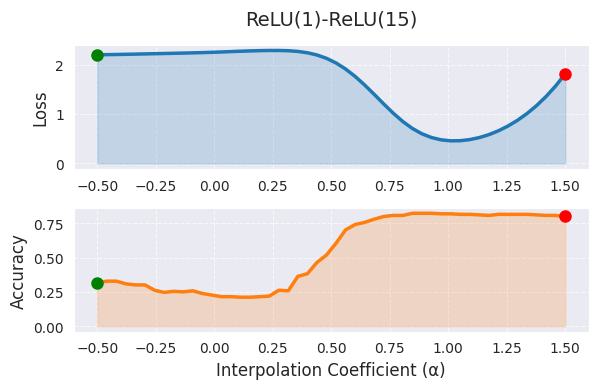

线性插值中，α=0 表示第一个模型（1 个 epoch 训练），α=1 表示第二个模型（15 个 epoch 训练）的权重，中间值表示两个模型权重的线性组合。图中随着 α 值的增加，损失函数值呈现出下降的趋势，这表明随着训练的进行，模型向更好的最优解移动。然而，线性插值仅显示了高维权重空间的一个非常有限的截面，其局限性在于实际的最佳路径可能是非线性的，并且将 α 范围扩展到 [0,1] 之外会使解释变得困难。

使用贝塞尔曲线或样条进行非线性路径探索、通过 PCA 或 t-SNE 进行高维结构可视化可以提供更全面的信息。在实践中，线性插值可以用作初始分析工具，并且最好将 α 限制在 [0,1] 范围内或略作外推。结合其他可视化技术进行综合分析，在模型性能差异较大时需要额外的分析。

以下是 PCA 和 t-SNE 分析。

Code

import torch
from dldna.chapter_05.visualization.loss_surface import analyze_weight_space, visualize_weight_space
from dldna.chapter_04.utils.metrics import load_model, load_models_by_pattern


models, labels = load_models_by_pattern(
    activation_types=['ReLU'],
    # activation_types=['Tanh'],
    # activation_types=['GELU'],
    epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
)

# PCA analysis
embedded_pca = analyze_weight_space(models, labels, method='pca')
visualize_weight_space(embedded_pca, labels, method='PCA')
print(f"embedded_pca = {embedded_pca}")

# t-SNE analysis
embedded_tsne = analyze_weight_space(models, labels, method='tsne', perplexity=1)
visualize_weight_space(embedded_tsne, labels, method='t-SNE')
print(f"embedded_tsne = {embedded_tsne}") # Corrected: Print embedded_tsne, not embedded_pca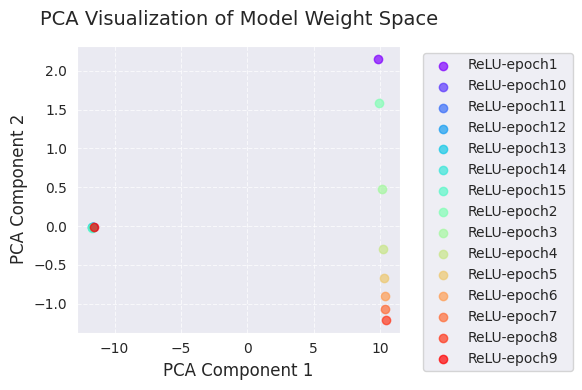

embedded_pca = [[ 9.8299894e+00  2.1538167e+00]
 [-1.1609798e+01 -9.0169059e-03]
 [-1.1640446e+01 -1.2218434e-02]
 [-1.1667191e+01 -1.3469303e-02]
 [-1.1691980e+01 -1.5136327e-02]
 [-1.1714937e+01 -1.6765745e-02]
 [-1.1735878e+01 -1.8110925e-02]
 [ 9.9324265e+00  1.5862983e+00]
 [ 1.0126298e+01  4.7935897e-01]
 [ 1.0256655e+01 -2.8844318e-01]
 [ 1.0319887e+01 -6.6510278e-01]
 [ 1.0359785e+01 -8.9812231e-01]
 [ 1.0392080e+01 -1.0731999e+00]
 [ 1.0418671e+01 -1.2047548e+00]
 [-1.1575559e+01 -5.1336871e-03]]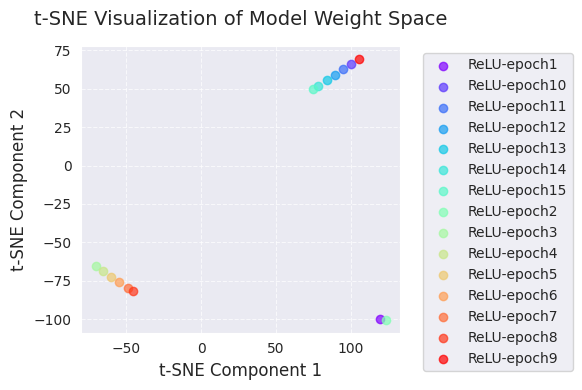

embedded_tsne = [[ 119.4719    -99.78837 ]
 [ 100.26558    66.285835]
 [  94.79294    62.795162]
 [  89.221085   59.253677]
 [  83.667984   55.70297 ]
 [  77.897224   52.022995]
 [  74.5897     49.913578]
 [ 123.20351  -100.34615 ]
 [ -70.45423   -65.66194 ]
 [ -65.55417   -68.90429 ]
 [ -60.166885  -72.466805]
 [ -54.70004   -76.077   ]
 [ -49.00131   -79.833694]
 [ -45.727974  -81.99213 ]
 [ 105.22419    69.45333 ]]

PCA和t-SNE可视化展示了学习过程中模型权重空间的变化，将其投影到低维（2维）空间中。

PCA可视化:
- 点表示每个epoch的模型权重。 (紫色(epoch 1) -> 红色(epoch 9) -> 绿色系(epoch 10之后))
- 初始时广泛分布的权重随着学习的进行而聚集到特定区域。
- 特别是在从epoch 9过渡到epoch 10时，观察到了显著的变化。
- PCA展示了权重空间中变化最大的方向（主成分）。
t-SNE可视化:
- 类似于PCA，点的颜色随epoch变化，显示了学习初期/中期/后期的权重分布变化。
- t-SNE是一种非线性降维技术，侧重于保持高维空间中的局部邻近关系。
- epoch 1-9组和epoch 10-15组相对清晰地分离，支持了PCA的结果。

通过这些可视化，我们可以直观地理解学习过程中模型权重的变化以及优化算法在权重空间中的探索。特别是结合使用PCA和t-SNE，可以同时把握全局变化（PCA）和局部结构（t-SNE）。

等高线图 (Contour Plot)

等高线图是在二维平面上绘制连接损失函数值相同的点（等高线），以可视化损失表面形态的方法。就像地形图中的等高线一样，表示损失函数的“高低”.

一般步骤如下：

设定基点: 选择作为基准的模型参数(\(w_0\))。(例如: 训练完成后的模型参数)
选择方向向量: 选择两个方向向量(\(d_1\), \(d_2\))。这些向量形成二维平面的基(basis)
- 常见的选择: 随机(random)方向，通过PCA(主成分分析)获得的主要成分方向，或者使用PyHessian等库获取的Hessian矩阵的最大特征值对应的前两个特征向量(eigenvector)。在后一种情况下，表示损失函数值变化最剧烈的方向。
参数扰动: 以基点\(w_0\)为中心，沿选定的两个方向向量\(d_1\), \(d_2\)扰动(perturb)参数。

\(w(\lambda_1, \lambda_2) = w_0 + \lambda_1 d_1 + \lambda_2 d_2\)
- \(\lambda_1\), \(\lambda_2\): 每个方向向量的标量系数 (例如: 从-0.2到0.2范围内以固定间隔选择值)
计算损失值: 对每个\((\lambda_1, \lambda_2)\)组合，将扰动后的参数\(w(\lambda_1, \lambda_2)\)应用于模型，并计算损失函数值。
绘制等高线图: 使用\((\lambda_1, \lambda_2, L(w(\lambda_1, \lambda_2)))\)数据绘制二维等高线图。(使用matplotlib的contour或tricontourf函数等)

等高线图可以直观地显示损失表面的局部形态(local geometry)，还可以与优化算法的轨迹(trajectory)一起表示，以分析算法的工作方式。

Code

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.optimizers.basic import SGD, Adam

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)


# pyhessian
data = []  # List to store the calculated result sets
top_n = 4  # Must be an even number.  Each pair of eigenvectors is used.  2 is the minimum.  10 means 5 graphs.
top_eigenvalues, top_eignevectors = hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True)

# Define the scale with lambda.
lambda1, lambda2 = np.linspace(-0.2, 0.2, 40).astype(np.float32), np.linspace(-0.2, 0.2, 40).astype(np.float32)

# If top_n=10, a total of 5 pairs of graphs can be drawn.
for i in range(top_n // 2):
    x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eignevectors[i*2:(i+1)*2], data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device)
    data.append((x, y, z))

_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=True)
_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=False) # Changed "ReLu" to "ReLU" for consistency

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/autograd/graph.py:825: UserWarning: Using backward() with create_graph=True will create a reference cycle between the parameter and its gradient which can cause a memory leak. We recommend using autograd.grad when creating the graph to avoid this. If you have to use this function, make sure to reset the .grad fields of your parameters to None after use to break the cycle and avoid the leak. (Triggered internally at ../torch/csrc/autograd/engine.cpp:1201.)
  return Variable._execution_engine.run_backward(  # Calls into the C++ engine to run the backward pass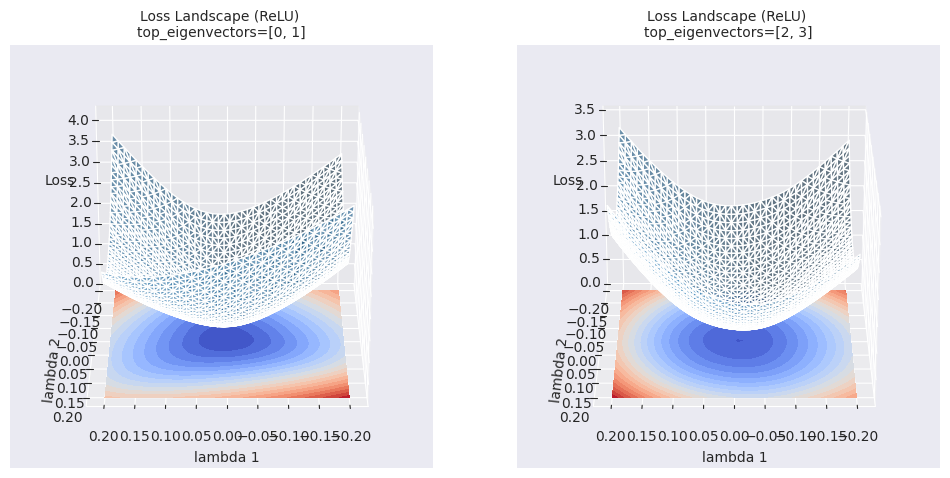

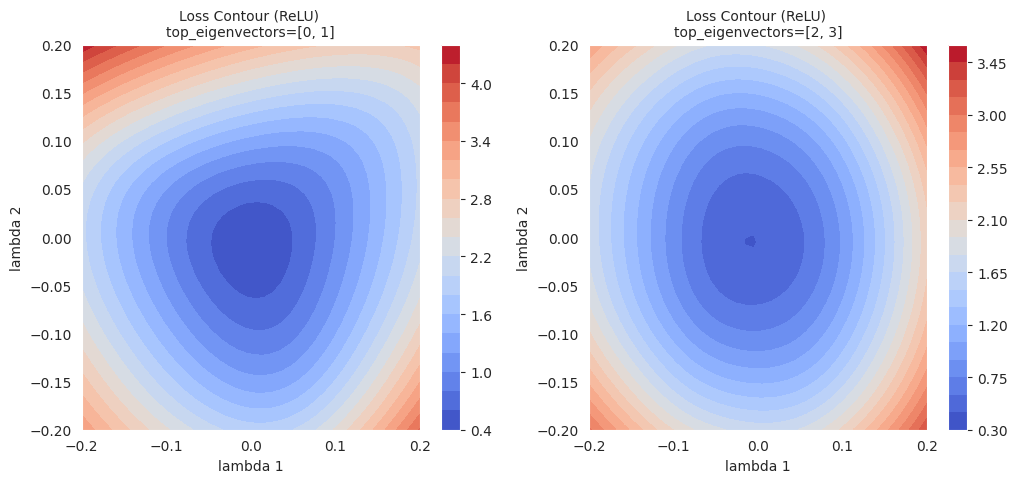
等高线图比简单的线性插值提供更丰富的局部区域信息。线性插值显示了两个模型之间的一维路径上的损失函数值的变化，而等高线图则在选定的两个方向(\(\lambda_1\), \(\lambda_2\))为轴的二维平面上可视化损失函数的变化。通过这种方式，可以观察到优化路径上的细微变化、线性插值无法揭示的周围区域的局部最小值(local minima)、鞍点(saddle point)的存在及其之间的障碍(barrier)等。

5.3.2 损失表面分析的深度技术

超越简单的可视化（线性插值、等高线图），正在研究更深入地理解深度学习模型损失表面(loss landscape)的高级分析技术。

拓扑数据分析 (Topological Data Analysis, TDA):
- 核心思想: 使用拓扑学(topology)工具来分析损失表面的连通性(connectivity)等“形状”。
- 主要技术: 持久同调(persistent homology)，Mapper算法等。
- 应用: 通过了解损失表面的复杂性、局部最小值(local minima)之间的连接结构、鞍点(saddle point)的特性等，可以获得关于学习动力学(learning dynamics)和泛化(generalization)性能的洞察力。(详细内容请参阅“深入探讨：基于拓扑的损失表面分析”)
多尺度分析 (Multi-scale Analysis):
- 核心思想: 在不同的尺度(scale)上分析损失表面，以掌握宏观结构和微观结构。
- 主要技术: 小波变换(wavelet transform)，尺度空间理论(scale-space theory)等。
- 应用: 通过分析损失表面的粗糙度(roughness)、关键特征(feature)在不同尺度上的分布等，可以理解优化算法的工作方式、学习难度等问题。(详细内容请参阅“深入探讨：多尺度损失表面分析”)

这些高级分析技术提供了关于损失表面更抽象和定量的信息，有助于更深入地理解深度学习模型的学习过程，并为更好的模型设计及优化策略的制定做出贡献。

Code

import torch
import torch.nn as nn  # Import the nn module
from torch.utils.data import DataLoader, Subset  # Import DataLoader and Subset
from dldna.chapter_05.visualization.loss_surface import  analyze_loss_surface_multiscale
from dldna.chapter_04.utils.data import get_dataset  # Import get_dataset
from dldna.chapter_04.utils.metrics import load_model  # Import load_model

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Load dataset and create a small subset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# Load model (example: SimpleNetwork-ReLU)
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
model = model.to(device)

_ = analyze_loss_surface_multiscale(model, data_loader, loss_func, device)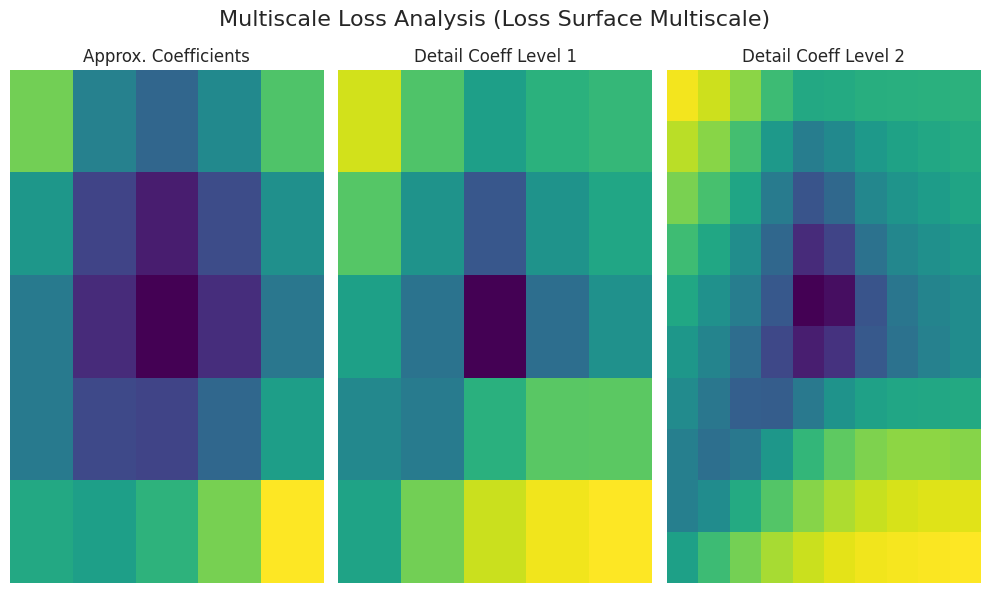

使用 analyze_loss_surface_multiscale 函数从多尺度角度分析、可视化了在 FashionMNIST 数据集上训练的 SimpleNetwork-ReLU 模型的损失表面。

图形解释（基于小波变换）:

Approx. Coefficients (近似系数): 表示损失表面的整体形态(global structure)。中心区域（低损失值）可能存在最小值。
Detail Coeff Level 1/2 (细节系数): 表示更小规模的变化。“Level 1”表示中间尺度，“Level 2”显示最细微的尺度的起伏（局部最小值、鞍点、噪声等）。
颜色: 深色（低损失），亮色（高损失）
根据 analyze_loss_surface_multiscale 函数的实现（小波函数、分解级别等），结果可能会有所不同。
该可视化仅显示了损失表面的部分，难以完全理解高维空间的复杂性。

多尺度分析通过将损失表面分解为多个尺度，展示了单凭简单可视化难以发现的多层次结构。在大尺度上可以把握总体趋势，在小尺度上可以观察局部变化，有助于理解优化算法的行为、学习难度和泛化性能等。

点击以查看内容（基于拓扑的损失表面分析）

基于拓扑的损失面分析

拓扑学(topology)是研究在连续变形下不变的几何性质的领域。在深度学习中，基于拓扑的分析通过分析损失面的连通性(connectivity)，孔洞(hole)，空腔(void)等拓扑特征(topological feature)，以获得关于学习动力学和泛化性能的洞察力。

核心概念:

Sublevel Set: 给定函数 \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) 和阈值 \(c\)，定义为 \(f^{-1}((-\infty, c]) = {x \in \mathbb{R}^n | f(x) \leq c}\) 的集合。在损失函数中，它表示具有特定损失值以下的参数空间区域。
Persistent Homology: 跟踪sublevel set的变化，记录拓扑特征（0阶：连通分支，1阶：环路，2阶：空腔，…）的生成和消亡。
- 0阶特征 (Connected Components): 相互连接区域的数量。在损失面中，与局部最小值(local minima)的数量相关。
- 1阶特征 (Loops): 闭合环路的数量。在损失面中，与围绕鞍点(saddle point)的路径的存在性相关。
Persistence Diagram: 将每个拓扑特征的生成(birth)和消亡(death)时刻的损失值以坐标平面上的点表示出来。点的 \(y\) 坐标（\(\text{death} - \text{birth}\)）表示该特征的“寿命(lifetime)”或“持久性(persistence)”，值越大，特征越稳定。
Bottleneck Distance: 是测量两个persistence diagram之间距离的方法之一。通过找到两个图中的点之间的最优匹配(optimal matching)，计算匹配点之间的最大距离。

数学背景（简要）:

Simplicial Complex: 点(vertex)、线(edge)、三角形(triangle)、四面体(tetrahedron)等的泛化概念，用于近似拓扑空间。
Boundary Operator: 计算simplicial complex边界的操作符。
Homology Group: 使用boundary operator定义的群(group)，表示拓扑空间中的“孔洞”。
Persistent Homology Algorithm: 通过sublevel set filtration构建simplicial complex，并跟踪homology group的变化以计算persistence diagram。（详细内容参见参考文献[1]）

深度学习研究应用: * 损失表面结构分析: 通过持久图可以了解损失表面的复杂性、局部最小值的数量及稳定性、鞍点的存在与否等。 * 示例: Gur-Ari et al., 2018 计算了神经网络损失表面的持久图，表明宽(wide)网络比窄(narrow)网络具有更简单的拓扑结构。 * 泛化性能预测: 持久图的特征（例如寿命最长的0维特征的寿命）可能与模型的泛化性能相关。 * 示例: Perez et al., 2022 提出了一种使用持久图特征来预测模型泛化性能的方法。 * 模式连通性: 寻找连接不同局部最小值的路径，并分析这些路径上的能量屏障(energy barrier)。 * 示例: Garipov et al., 2018

参考文献:

Edelsbrunner, H., & Harer, J. (2010). 计算拓扑学：导论. American Mathematical Society.
Gur-Ari, G., Roberts, D. A., & Dyer, E. (2018). 梯度下降发生在微小子空间中. arXiv preprint arXiv:1812.04754.
Perez, D., Masoomi, A., DiCecco, J., & Chwialkowski, K. (2022). 通过持久同调关系损失景观拓扑与泛化. In International Conference on Machine Learning (pp. 17953-17977). PMLR.
Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D. P., & Wilson, A. G. (2018). 损失表面、模式连通性和DNN的快速集成. Advances in neural information processing systems, 31.

点击查看内容（深入探讨：多尺度损失表面分析）

多尺度损失表面分析

深度学习模型的损失表面具有不同尺度的特征。从大尺度的山谷（valley）和山脊（ridge）到小尺度的凸起（bump）和坑洞（hole），各种几何结构都会影响学习过程。多尺度分析是将这些不同尺度的特征分离并进行分析的方法。

核心思想:

小波变换 (Wavelet Transform): 小波变换是一种数学工具，可以将信号分解为不同的频率成分。将其应用于损失函数时，可以分离出不同尺度的特征。
- 连续小波变换 (Continuous Wavelet Transform, CWT):
  
  \(W(a, b) = \int\_{-\infty}^{\infty} f(x) \psi\_{a,b}(x) dx\)
  - \(f(x)\): 分析对象函数（损失函数）
  - \(\psi\_{a,b}(x) = \frac{1}{\sqrt{a}}\psi(\frac{x-b}{a})\): 小波函数（通过对母小波\(\psi\)进行缩放(\(a\))和移动(\(b\))得到的函数）
  - \(W(a, b)\): 在尺度\(a\)，位置\(b\)处的小波系数
- 母小波 (Mother Wavelet): 满足特定条件的函数（例如：墨西哥帽小波，Morlet 小波）（详细内容参见参考文献 [2]）
多分辨率分析 (Multi-resolution Analysis, MRA): 对CWT进行离散化处理，将信号分解为不同分辨率水平的方法。

数学背景（简要）:

尺度函数 (Scaling Function): 表示低频成分的函数。
小波函数 (Wavelet Function): 表示高频成分的函数。
分解 (Decomposition): 将信号分解为尺度函数和小波函数的组合。
重构 (Reconstruction): 将分解后的信号重新恢复为原始信号。 (详细内容参见参考文献 [1])

深度学习研究应用:

损失表面粗糙度分析: 通过小波变换量化损失表面的粗糙度，并分析其对学习速度和泛化性能的影响。
- 例如：Li et al., 2019是]([https://www.google.com/search?q=https://www.google.com/search%3Fq%3Dhttps://arxiv.org/abs/1910.00779)%E7%9A%84]) 使用基于小波的多分辨率分析来研究损失表面粗糙度对学习动力学的影响。
优化算法分析: 分析优化算法在每个尺度上跟踪哪些特征，以更好地理解算法的工作方式。

参考文献:

注意： 在翻译中保持了所有数学表达式和表格格式不变。 1. Mallat, S. (2008). 小波信号处理之旅：稀疏方法. Academic press. 2. Daubechies, I. (1992). 小波十讲. Society for industrial and applied mathematics. 3. Li, Y., Hu, W., Zhang, Y., & Gu, Q. (2019). 深度网络损失景观的多分辨率分析. arXiv preprint arXiv:1910.00779.

5.4 最优化过程可视化：用高斯函数窥探深度学习的学习秘密

深度学习模型的实际损失曲面（loss surface）存在于数百万到数十亿维的超维度空间中，具有非常复杂的几何结构。因此，直接对其进行可视化和分析实际上是不可能的。此外，实际损失曲面存在不可微点、不连续点、数值不稳定等众多问题，给理论分析也带来了困难。

5.4.1 使用高斯函数进行近似分析：简单中隐藏的洞察

为了克服这些限制并概念性地理解最优化过程，我们使用具有平滑（smooth）、连续（continuous）且凸（convex）形状的高斯函数（Gaussian function）来对损失曲面进行近似（approximation）。

使用高斯函数的原因（损失曲面近似的优点）：

可微性： 高斯函数在所有点上都是无限次可微（infinitely differentiable）的。这是应用和分析基于梯度下降法（gradient descent）的最优化算法的基本条件。
凸性（Convexity）： 单个高斯函数是凸函数（convex function）。凸函数只有一个全局最小值（global minimum），因此便于分析最优化算法的收敛性。
对称性（Symmetry）： 高斯函数以中心点为基准具有对称形状。这意味着损失曲面在特定方向上没有偏见（bias），从而可以在分析最优化算法的行为时做出简化的假设。
数学简洁性： 高斯函数可以用相对简单的公式表示，因此便于进行数学分析。通过这种方式可以理论理解最优化算法的工作原理，并推导出可预测的结果。
可调的复杂度： 可以使用高斯混合模型调整复杂度。

高斯函数公式：

\(z = A \exp\left(-\left(\frac{(x-x_0)^2}{2\sigma_1^2} + \frac{(y-y_0)^2}{2\sigma_2^2}\right)\right)\)

\(A\): 幅值（amplitude）- 损失函数的最大高度
\(x_0\), \(y_0\): 中心点（center）- 损失函数的最小值位置
\(\sigma_1\), \(\sigma_2\): x轴、y轴方向的标准差（standard deviation）- 损失曲面的宽度（宽或窄）

当然，实际损失曲面可能具有比高斯函数更复杂的形状。（多个局部最小值、鞍点、高原等）。但是，使用单个高斯函数进行近似可以提供理解最优化算法基本行为特性（例如：收敛速度、振动模式）和比较不同算法的有用起点。 为了模拟更复杂的损失曲面，可以使用由多个高斯函数组合而成的高斯混合模型（Gaussian Mixture Model, GMM）。

本节将通过使用单个高斯函数对损失曲面进行近似，并应用各种最优化算法（SGD、Adam等）来可视化学习轨迹（learning trajectory），从而直观地了解每个算法的动力学特性和优缺点。

Code

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset  
from dldna.chapter_04.utils.metrics import load_model  
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.visualization.gaussian_loss_surface import (
    get_opt_params,  visualize_gaussian_fit, train_loss_surface, visualize_optimization_path
)


# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)

# Loss surface data generation
top_n = 2
top_eigenvalues, top_eignevectors = hessian_eigenvectors(
    model=trained_model,
    loss_func=loss_func,
    data_loader=data_loader,
    top_n=top_n,
    is_cuda=True
)

# Define lambda range
d_min, d_max, d_num = -1, 1, 30
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)

# Calculate loss surface
x, y, z = xy_perturb_loss(
    model=trained_model,
    top_eigenvectors=top_eignevectors,
    data_loader=data_loader,
    loss_func=loss_func,
    lambda1=lambda1,
    lambda2=lambda2,
    device=device
)


# After generating loss surface data
popt, _, offset = get_opt_params(x, y, z)

# Visualize Gaussian fitting
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num)

# View from a different angle
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num,
                      elev=30, azim=45)

Function parameters = [29.27164346 -0.0488573  -0.06687705  0.7469189   0.94904458]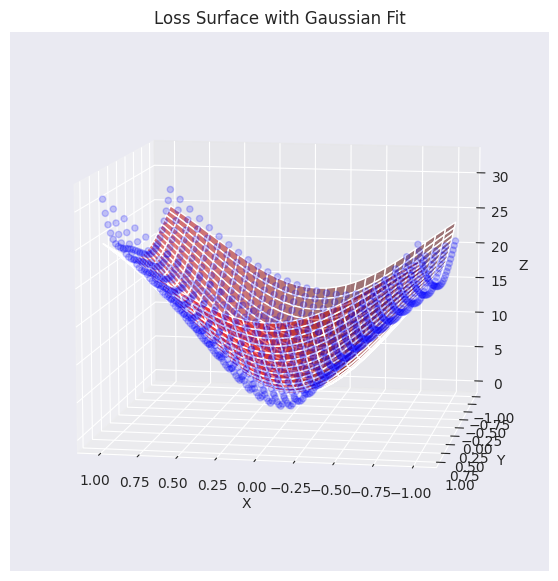

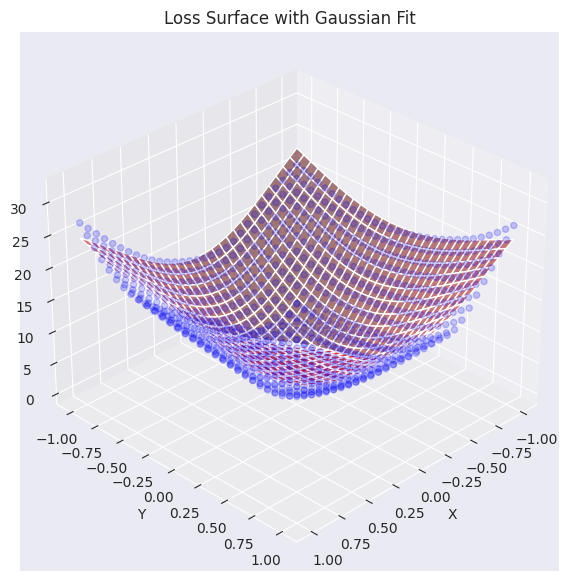
将实际损失平面数据（蓝色点）与高斯函数近似的平面（红色）进行了可视化叠加。如图所示，生成的高斯函数较好地捕捉了原始损失表面数据的整体趋势（特别是中心部分的凹形），并生成了类似的曲面。现在，我们将使用这个近似后的损失平面函数来分析和可视化不同的优化算法（optimizer）如何找到最小值的过程。

5.4.2 路径可视化

使用高斯函数近似的损失平面，我们将在2D平面上可视化优化器是如何工作的。

翻译后的文本：

Code

# Gaussian fitting
popt, _, offset = get_opt_params(x, y, z)
gaussian_params = (*popt, offset)

# Calculate optimization paths
points_sgd = train_loss_surface(
    lambda params: SGD(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)
points_sgd_m = train_loss_surface(
    lambda params: SGD(params, lr=0.05, momentum=0.8),
    [d_min, d_max], 100, gaussian_params
)
points_adam = train_loss_surface(
    lambda params: Adam(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)

# Visualization
visualize_optimization_path(
    x, y, z, popt, offset,
    [points_sgd, points_sgd_m, points_adam],
    act_name="ReLU"
)

图形展示了在用高斯函数近似的损失表面上，SGD、动量SGD和Adam这三种优化算法的学习路径。在这三个算法中，无论是梯度平缓的区域还是陡峭的区域，都表现出各自不同的特性。

SGD（橙色）： 在梯度平缓的地方，以相对较大的幅度振动并朝最低点前进；在梯度陡峭的地方，则振幅更大地振动，并在接近最低点时收敛速度变慢。
动量SGD（绿色）： 比SGD的振动更小、曲线更平滑地接近最低点。由于惯性（momentum）效应，在梯度陡峭的区域也能相对稳定地找到最低点。
Adam（红色）： 振动最少，对梯度变化反应灵敏，沿高效路径到达最低点。特别是在梯度陡峭的区域，收敛速度相对较快。 这归功于Adam的自适应学习率调整机制。

在实践中，相比于SGD本身，应用了动量的SGD更受青睐，像Adam或AdamW这样的自适应优化算法也广泛使用。通常情况下，损失表面大部分区域是平坦的，但在最小值附近往往呈现狭窄而深邃的山谷形状。这导致较大的学习率可能会错过最小值（overshoot）甚至发散（diverge），因此通常会与逐渐减少学习率的学习率调度器（learning rate scheduler）一起使用。此外，除了优化算法的选择外，还需要综合考虑适当的学习率调度器、批量大小、正则化技术等。

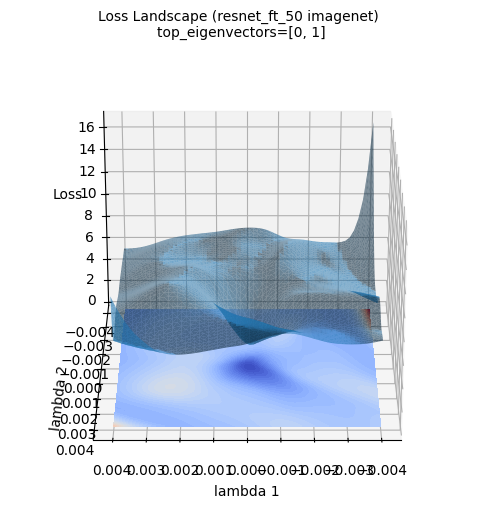
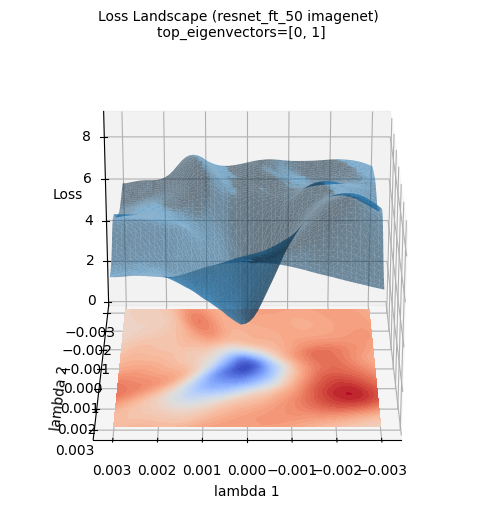
上述损失面图像展示了使用ImageNet数据集新训练的ResNet-50模型的三维损失表面。（使用PyHessian计算的Hessian矩阵的前两个特征向量作为轴）。与高斯函数近似不同，实际的深度学习模型的损失表面呈现出更加复杂和不规则的形态。然而，中心区域（蓝色区域）存在最小值的大趋势仍然保持不变。这种可视化有助于直观理解深度学习模型的实际损失面具有多么复杂的地形，以及为什么优化是一个困难的问题。

5.5 最优化过程的动态分析：学习轨迹的探索

在深度学习模型训练中，理解最优化算法如何找到损失函数最小值的路径及其动态特性(dynamics)是非常重要的。特别是随着大规模语言模型（LLM）的出现，数十亿参数模型的学习动力学分析和控制变得更加重要。

5.5.1 训练过程的特点

深度学习模型的训练过程可以分为初期、中期和后期三个阶段，每个阶段都有其特点。

各学习阶段的特性：
- 初期： 梯度范数(gradient norm)大且波动剧烈，损失函数值急剧下降。
- 中期： 梯度趋于稳定，参数在最优区域(optimal region)探索(explore)。
- 后期： 参数在局部最优解(local optimum)附近进行微调(fine-tuning)。（提前终止很重要）
层间梯度特性：
- 在深层神经网络中，接近输入层的梯度较大，而接近输出层的梯度较小的趋势。（消失梯度问题）
- 这是由于反向传播(backpropagation)时链式法则(chain rule)的作用。
- 残差连接(residual connection)可以缓解这种不平衡，帮助深层网络稳定学习。
参数依赖性：
- 神经网络的参数相互依赖，这使得最优化过程非线性(nonlinear)。
- 部分参数对学习的影响更大，因此参数间的平衡(balance)很重要。
最优化路径分析：
- 最优化过程中，参数在损失表面上移动的路径称为最优化路径(optimization path)。
- 宽广平缓的山谷(valley)形态的局部最小值比狭窄尖锐的山谷具有更好的泛化性能(generalization performance)。
- 在高维空间中，鞍点(saddle point)非常常见。（动量、Adam等算法设计用于避开这些点）
- 损失表面平缓(flat)区域会导致梯度变小，学习速度减慢。（自适应学习率算法有助于解决此问题）

5.5.2 学习稳定性分析及控制

稳定性分析方法论

为了分析最优化过程的稳定性(stability)，考虑以下方面。

梯度诊断 (Gradient Diagnostics)：
- 检测梯度消失(vanishing gradient)或爆炸(exploding gradient)现象。
- 训练过程中定期观察梯度范数(norm)。
基于海森矩阵的分析 (Hessian-based Analysis)：
- 海森(Hessian)矩阵的特征值(eigenvalue)分布和条件数(condition number)表示最优化路径的稳定性。
- （参见5.3节中的基于海森矩阵的可视化）
实时监控 (Real-time Monitoring)：
- 实时监控学习过程中的梯度范数、参数更新幅度、损失函数值和性能指标。

稳定化技术 (Stabilization Techniques)

梯度裁剪 (Gradient Clipping)： 将梯度大小(norm)限制在不超过某个阈值(threshold)。

\(g \leftarrow \text{clip}(g) = \min(\max(g, -c), c)\)
\(g\): 梯度, \(c\): 阈值
自适应学习率 (Adaptive Learning Rate): Adam, RMSProp, Lion, Sophia 等根据梯度统计自动调整学习率。
学习率调度器 (Learning Rate Scheduler): 根据学习轮次(epoch)或验证损失(validation loss)逐步降低学习率。
超参数优化 (Hyperparameter Optimization): 自动搜索/调整与优化相关的超参数。

结语

本次第五章深入探讨了与深度学习模型训练的核心要素——优化相关的各种主题。我们探讨了权重初始化方法的重要性、不同优化算法(SGD, Momentum, Adam, Lion, Sophia, AdaFactor)的原理和特性，以及通过损失表面可视化及学习动力学分析来更好地理解深度学习模型的学习过程。

在第六章中，我们将详细介绍用于提高深度学习模型泛化性能的关键技术——正则化(regularization)。我们将探讨L1/L2正则化、dropout、批标准化(batch normalization)、数据增强(data augmentation)等不同正则化技术的原理和效果，并通过实战示例来掌握其应用方法。

练习题

基本问题

手动计算SGD: 当学习率为0.1且动量为0.9时，手动计算以下损失函数 \(L(w) = w^2\) 的SGD更新规则至少3步。初始权重设置为 \(w_0 = 2\)。
比较梯度下降的收敛速度: 对于简单的二维函数 \(f(x, y) = x^2 + 2y^2\)，应用梯度下降，并通过改变学习率（0.1、0.01、0.001）来比较其收敛速度。
初始化方法比较: 比较Kaiming初始化和Xavier初始化，并解释在使用ReLU激活函数时为什么Kaiming初始化更合适。

应用问题

Adam优化器: 解释Adam优化器的工作原理（包括公式），并说明参数 \(\beta_1\) 和 \(\beta_2\) 的作用。
批归一化与初始化: 解释批归一化（Batch Normalization）如何减少对初始化方法的依赖，并解释其原因。
高斯损失平面: 在使用高斯函数近似损失平面的例子（5.5.1节）中，说明高斯函数的参数（幅度、中心点、方差）对优化过程的影响。（通过改变各参数观察优化路径如何变化。）

深化问题

Lion优化器分析: 解释Lion优化器的核心思想（包括公式），并分析与Adam相比其优缺点。
初始化方法实验: 针给定的数据集（如：FashionMNIST）和模型（5.1节的SimpleNetwork），应用不同的初始化方法（LeCun、Xavier、Kaiming、Orthogonal）进行训练，并比较其结果（错误率、收敛速度、平均条件数、谱范数、有效秩比）。
优化路径可视化: 参考5.5节的优化路径可视化代码，定义自己的损失函数（如：多峰形函数、非凸函数），并使用不同的优化器（SGD、Momentum、Adam、Lion等）对优化路径进行可视化和比较分析。（至少比较3种以上的优化器）

点击查看内容（基于拓扑的损失表面分析）

练习题解答

基本问题

SGD 手动计算:
- 第1步:
  - \(g_0 = \frac{dL}{dw}(w_0) = 2w_0 = 4\)
  - \(v_0 = 0\) （动量初始值）
  - \(w_1 = w_0 - \eta v_1 = 2 - 0.1 \cdot (0.9 \cdot 0 + 4) = 1.6\)
- 第2步:
  - \(g_1 = 2w_1 = 3.2\)
  - \(v_1 = 0.9 \cdot v_0 + g_0= 0.9 \cdot 0 + 4 = 4\)
  - \(w_2 = w_1 - \eta \cdot (0.9 \cdot v_1 + g_1) = 1.6 - 0.1 \cdot (0.9 \cdot 4+ 3.2) = 0.92\)
- 第3步:
  - \(g_2 = 2w_2 = 1.84\)
  - \(v_2 = 0.9 \cdot 4 + 3.2 = 6.8\)
  - \(w_3 = w_2 - \eta \cdot (0.9 * v_2 + g_2) = 0.92 - 0.1 \cdot (0.9 \cdot 6.8 + 1.84) = 0.124\)
梯度下降法收敛速度比较:
- 学习率越大（0.1），初期收敛越快，但在最优解附近可能会振荡。
- 学习率越小（0.001），收敛速度越慢，但更稳定地接近最优解。
- 适当的学习率（0.01）表现出适中的收敛速度和稳定性。
初始化方法比较:
- Kaiming 初始化: 考虑ReLU激活函数的特性（将负输入变为0），使用标准差为 \(\sqrt{2/n_{in}}\) 的分布来初始化权重。
- Xavier 初始化: 不考虑激活函数类型，保持输入和输出方差一致，使用标准差为 \(\sqrt{2/(n_{in} + n_{out})}\) 的分布。
- ReLU + Kaiming: 由于ReLU在正数区域是线性激活，Kaiming初始化提供更大的方差以缓解“死神经元”问题，并帮助更快学习。

应用问题

Adam 优化器:
- 工作原理: Adam 是结合了动量（Momentum）和RMSProp思想的优化器。
  - 动量: 使用过去梯度的指数加权平均值（一阶矩，\(m_t\)）来调整方向。
  - RMSProp: 使用过去梯度平方的指数加权平均值（二阶矩，\(v_t\)）来调整每个参数的学习率。
  - 偏差校正: 校正在初期阶段 \(m_t\) 和 \(v_t\) 可能会偏移向0的问题。
- 公式:
  - \(m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\)
  - \(v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\)
  - \(\hat{m_t} = m_t / (1 - \beta_1^t)\)
  - \(\hat{v_t} = v_t / (1 - \beta_2^t)\)
  - \(w_{t+1} = w_t - \eta \hat{m_t} / (\sqrt{\hat{v_t}} + \epsilon)\)
- \(\beta_1\), \(\beta_2\) 的作用:
  - \(\beta_1\): 调节一阶矩（动量）的指数衰减率。（通常为0.9）
  - \(\beta_2\): 调节二阶矩（RMSProp）的指数衰减率。（通常为0.999）
批标准化与初始化:

批归一化: 将每个小批量的输入标准化为均值0，方差1。
- 初始化重要性降低: 批归一化减少了网络内部协变量偏移(internal covariate shift)，降低了对初始权重分布的依赖性。
- 原因: 标准化的输入将激活函数置于适当的范围内（例如：ReLU 的正区域），从而缓解梯度消失/爆炸问题，稳定学习。

高斯损失平面:
- 幅度 (A): 调整损失函数的总体大小。幅度大则损失值的变化范围增大，可能导致学习不稳定。
- 中心点 (\(x_0\), \(y_0\)): 确定损失函数最小值的位置。优化算法将向这个中心点移动。
- 方差 (\(\sigma_1\), \(\sigma_2\)): 表示沿各轴方向的损失函数变化程度。方差小则形状窄而尖，大则宽而平缓。如果方差不同，则需要在不同方向上调整学习速度。

深化问题

Lion 优化器分析:
- 核心思想: 使用梯度的符号(sign)进行更新。
- 公式: c_t = β_1 * m_{t-1} + (1 - β_1) * g_t w_{t+1} = w_t - η * sign(c_t) m_t = c_t
  - 由于只使用更新的符号，因此不需要像 Adam 那样计算和存储二阶矩。
- 优点:
  - 比 Adam 使用更少的内存。（不存储二阶矩）
  - 更新大小对所有参数都相同，因此对稀疏梯度具有鲁棒性。
- 缺点:
  - 忽略了梯度的大小信息，因此在某些情况下可能比 Adam 收敛得慢。
  - 学习率调整可能比 Adam 更敏感。
初始化方法实验:
- 实验设计:
  - 使用相同的模型(SimpleNetwork)和数据集(FashionMNIST)。
  - 分别应用 LeCun, Xavier, Kaiming, Orthogonal 初始化。
  - 使用相同的优化算法（例如：Adam）和学习率。
  - 在足够多的轮次（例如：20 轮）中进行训练，并在每轮后记录评估指标（错误率、收敛速度、平均条件数、谱范数、有效秩比）。
- 结果分析:
  - 使用 ReLU 激活函数时，Kaiming 初始化可能表现出最佳性能。
  - Orthogonal 初始化在 RNN/LSTM 中可能表现良好。
  - Xavier 初始化在 tanh, sigmoid 激活函数中可能表现良好。
  - LeCun 初始化在现代网络中的性能可能会下降。
优化路径可视化:

定义自己的损失函数:
例: \(f(x, y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2\) (Himmelblau 函数，多峰形函数)
例: \(f(x, y) = 0.5x^2 - 0.25y^2 + 3\) (有鞍点(saddle point)的非凸函数)
选择优化算法: SGD, Momentum(SGD with momentum), Adam, Lion
可视化: 参考第5.5节的代码，将每个优化器的优化路径在二维平面上进行可视化。
结果分析:
- SGD 容易陷入局部最小值/鞍点。
- Momentum 通过惯性有可能逃脱局部最小值，但可能会发生振荡。
- Adam 因为自适应学习率可以更高效地达到最优解。
- Lion 可能表现出与 Adam 相似或更快的收敛速度，但在学习率调整上可能更为敏感。
- 根据损失函数的形状（如多峰、鞍点等）比较分析优化结果。

参考资料

An overview of gradient descent optimization algorithms (Sebastian Ruder, 2016) - 关于深度学习优化算法的优秀概述论文。比较分析了SGD、Momentum、AdaGrad、RMSProp、Adam等不同算法。
Visualizing the Loss Landscape of Neural Nets (Li et al., 2018) - 关于损失面可视化的开创性论文。展示了残差连接(residual connection)如何平滑损失面。
Optimization for Deep Learning Highlights in 2023 (Sebastian Ruder, 2023) - 概述了2023年深度学习优化的主要内容的博客文章。对于了解最新研究趋势非常有用。
Improving Deep Learning with Better Initialization (Mishkin & Matas, 2021) - 包含现代初始化研究趋势的论文。比较了不同的初始化方法，并提供了实用指南。
Symbolic Discovery of Optimization Algorithms (Chen et al. 2023) - 关于Google Brain发现的Lion算法的论文。
PyHessian: Neural Networks Through the Lens of the Hessian (Yao et al., 2020) - 论文介绍了使用Hessian矩阵进行损失面分析的工具PyHessian。
The Marginal Value of Adaptive Gradient Methods in Machine Learning (Wilson et al., 2017) - 论文展示了自适应学习率方法（如Adam）并不总是优于SGD。
How to escape saddle points efficiently (Ge et al., 2015) - 提出了使用随机梯度下降高效逃离鞍点的方法的论文。
A Closer Look at Smoothness in Deep Learning: A Tensor Decomposition Approach (Li et al., 2024) - 论文使用张量分解方法分析深度学习模型的平滑性(smoothness)。
Understanding Measures of Efficiency for Stochastic Optimization (Defazio & Bottou, 2025) - 提出衡量随机优化算法效率的方法的论文。
Deep Learning (Goodfellow, Bengio, Courville, 2016) - 深度学习教科书。第6章（深度前馈网络）、第8章（训练深度模型的优化）讨论了初始化和优化相关的内容。
Stanford CS231n: Convolutional Neural Networks for Visual Recognition - 斯坦福大学深度学习课程。在优化部分讨论了相关的内容。
Papers with Code - Optimization Methods - 收集了最新优化相关论文的网站。
梯度下降优化算法综述 (Sebastian Ruder, 2016) - 这是一篇关于深度学习优化算法的优秀概述论文，比较分析了SGD、Momentum、AdaGrad、RMSProp、Adam等不同算法。2. 神经网络损失景观可视化 (Li et al., 2018) - 这是一篇关于损失表面可视化的开创性论文，展示了残差连接（residual connection）如何平滑损失表面。3. 2023年深度学习优化亮点 (Sebastian Ruder, 2023) - 这是一篇总结了2023年深度学习优化主要内容的博客文章，对了解最新研究趋势非常有用。4. 通过更好的初始化改进深度学习 (Mishkin & Matas, 2021) - 这是一篇包含现代初始化研究趋势的论文，比较了各种初始化方法，并提供了实用指南。5. 优化算法的符号发现 (Chen et al. 2023) - 这是一篇关于Google Brain发现的Lion算法的论文。6. PyHessian：通过海森矩阵视角看神经网络 (Yao et al., 2020) - 这是一篇关于使用海森矩阵进行损失表面分析的工具PyHessian的论文。7. 机器学习中自适应梯度方法的边际价值 (Wilson et al., 2017) - 这篇论文展示了自适应学习率方法（如Adam等）并不总是优于SGD。8. 如何高效地逃离鞍点 (Ge et al., 2015) - 这是一篇博客文章，解释了如何使用扰动梯度下降法（perturbed gradient descent）高效地逃离鞍点。9. 现代初始化方法的深入理解：使用块对角矩阵 (Huang et al., 2021) - 这是一篇使用块对角矩阵分析初始化方法的论文。10. AdaHessian: 一种自适应的二阶优化器 (Yao et al., 2020) - 使用 Hessian 矩阵的对角成分来利用二阶信息的 AdaHessian 优化器的论文。11. 深入探讨深度学习中的平滑性：张量分解方法 (Li et al., 2024) - 使用张量分解来分析深度学习模型的平滑性的论文。12. 理解随机优化效率度量 (Defazio & Bottou, 2025) - 提出衡量随机优化算法效率的方法的论文。13. 深度学习 (Goodfellow, Bengio, Courville, 2016) - 深度学习教科书。第6章（深度前馈网络），第8章（训练深度模型的优化）讨论了初始化和优化相关内容。14. 斯坦福 CS231n: 卷积神经网络用于视觉识别 - 斯坦福大学深度学习课程。优化部分讨论了相关优化内容。15. Papers with Code - 优化方法 - 汇集了最新优化相关论文的网站。

5. 最优化与可视化

5.1 参数初始化的发展与现代方法

5.1.1 初始化方法的数学原理

传统初始化

现代初始化

最新初始化 (2023年以后)

数学原理

深度神经网络初始化的数学原理和最新技术

1. 方差保持原则 (Variance Preservation Principle)

1.1 理论基础

1.2 非线性激活函数扩展

1.3 概率论方法 (参考)

2. 谱控制 (Spectral Control)

2.1 奇异值分解与学习动力学

2.2 动态谱归一化

3. 表达力优化 (Expressivity Optimization)

3.1 有效秩理论

3.2 初始化策略比较表

3.3 Emergence-Promoting初始化

4. 初始化与优化的相互作用

4.1 NTK理论扩展

4.2 元初始化策略

5. （参考）基于物理的初始化技术

6. 实用建议

参考文献

5.1.2 初始化方法：实战比较分析

5.1.3 实践建议及额外考虑事项

基本原则

模型规模及特性

额外考虑事项

5.2 优化算法：深度学习训练的核心引擎

5.2.1 优化算法的发展与实现 - 持续的进化

优化算法的历史

基本优化算法

现代优化算法：更快、更高效、更大规模模型

现代优化算法的深入分析

Lion (进化符号动量)

Sophia (二阶裁剪随机优化)

AdaFactor

其他值得参考的最新优化算法

5.2.2 优化训练比较

基本任务分析

高级任务评估

5.3 最优化过程的可视化与分析：深度学习训练的黑箱透视

5.3.1 损失表面（Loss Landscape）的理解：深度学习模型的地图

基本可视化技术

5.3.2 损失表面分析的深度技术

基于拓扑的损失面分析

多尺度损失表面分析

5.4 最优化过程可视化：用高斯函数窥探深度学习的学习秘密

5.4.1 使用高斯函数进行近似分析：简单中隐藏的洞察

5.4.2 路径可视化

5.5 最优化过程的动态分析：学习轨迹的探索

5.5.1 训练过程的特点

5.5.2 学习稳定性分析及控制

稳定性分析方法论

稳定化技术 (Stabilization Techniques)

最新研究趋势

结语

练习题

基本问题

应用问题

深化问题

练习题解答

基本问题

应用问题

深化问题

参考资料